7.6: Гучність, орієнтація та тензор Леві-Чівіти

Цілі навчання

• Впровадження деяких геометричних машин, які використовуються як у спеціальній, так і в загальній теорії відносності

Цей необов'язковий розділ представляє деякі геометричні машини, які використовуються як у спеціальній, так і в загальній теорії відносності.

Обсяг

бажані властивості

У$3 + 1$ розмірах ми маємо природний спосіб визначення чотиривимірного об'єму, який полягає в тому, щоб вибрати систему відліку і дозволити елементу об'єму знаходитися$dt dx dy dz$ в координатах Мінковського цього кадру. Хоча це визначення$4$ -обсягу викладається в терміні певних координат, воно виявляється Лоренц-інваріантним (розділ 2.5). Він також має такі бажані властивості, які ми констатуємо для довільного значення$m$ from$1$ to$4$:

1. V1. Будь-які два$m$ -обсяги можна порівняти за їх співвідношенням.
2. V2. Для будь-яких$m$ ненульових векторів$m$ -обсяг паралелепіпеда, який вони охоплюють, є ненульовим тоді і лише тоді, коли вектори лінійно незалежні (тобто якщо жоден з них не може бути виражений через інші за допомогою скалярного множення та додавання векторів).

Також хотілося б мати зручні методи роботи з трьохтомними, двооб'ємними (площа) і однооб'ємними (довжина). Але$m$ -томи для$m < 4$ дають нам головні болі, якщо ми спробуємо визначити їх так, щоб вони підкорялися як V1, так і V2. Наприклад, очевидним способом визначення length ($m = 1$) є використання метрики, але тоді світлоподібні вектори порушуватимуть V2.

Аффінна міра

Якщо ми готові відмовитися від V1, то наступний підхід вдається. Розглянемо$m = 1$ випадок. Ми повністю ігноруємо метрику і експлуатуємо той факт, що в спеціальній теорії відносності spacetime flat (постулат P2), так що паралелізм працює так само, як і в евклідовій геометрії. $l$Дозволяти лінії, і припустимо, що ми хочемо визначити систему числення на цій лінії, яка вимірює, наскільки далеко один від одного події. Залежно від типу лінії, це може бути вимір часу, просторової відстані або суміш двох.

Малюнок$\PageIndex{1}$: Використання паралелізму для визначення 1-томи.

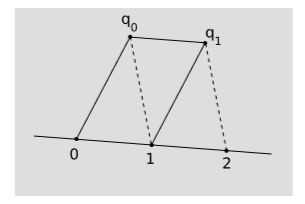
Спочатку довільно виділяємо дві різні точки на$l$ і маркуємо їх$0$ і$1$, як на малюнку$\PageIndex{1}$. Далі підберіть якусь допоміжну точку, що$q_0$ не лежить на$l$. Побудувати$q_0 q_1$ і паралельно$01$ і$1q_1$ паралельно$0q_0$, утворюючи паралелограм, показаний на малюнку. Продовжуючи таким чином, ми маємо риштування паралелограмів, що примикають до прямої, визначаючи нескінченну решітку точок$1, 2, 3, ...$ на прямій, які представляють собою натуральні числа. Дроби можуть бути визначені аналогічним чином. Наприклад,$\tfrac{1}{2}$ визначається як точка така, що коли початковий відрізок решітки$0\tfrac{1}{2}$ подовжується тією ж конструкцією, наступною точкою на решітці є$1$. Постійно мінлива змінна, побудована таким чином, називається афінним параметром. Час, виміряний годинником вільного падіння, є прикладом афінного параметра, як і відстань, виміряна галочками на вільно падаючої лінійці. Аффінний параметр можна визначити лише вздовж прямої світової лінії, а не довільної кривої. Афінне вимірювання$1$ -обсягу порушує V1, оскільки воно дозволяє нам лише порівнювати відстані, які лежать на ньому$l$ або паралельні йому. З іншого боку, він має перевагу перед метричним вимірюванням, що дозволяє нам вимірювати довжини вздовж світлоподібних ліній.

Малюнок$\PageIndex{2}$: Площа альта можна визначити, підрахувавши паралелограми, утворені гратами. Площа можна визначити з будь-якою потрібною точністю, розділивши паралелограми на дробові частини, які настільки малі, наскільки це необхідно.

На малюнку$\PageIndex{2}$ показано, як визначити афінну міру$2$ -обсягу, і подібний метод працює для$3$ -volume.

Лінійність

Малюнок$\PageIndex{3}$: Лінійність площі. Подвоєння вектора a подвоює площу.

Припустимо, що паралелограм утворений з векторами a і b як дві його сторони. Це ми подвоюємо а, то площа подвоюється, а також,

$$area(2a,b) = 2area(a,b)$$

Загалом, якщо ми масштабуємо будь-який з векторів за коефіцієнтом$c$, площа масштабується на той самий коефіцієнт, за умови, що ми встановимо якесь правило для обробки знаків - проблема, яку ми відкладемо до розділу Орієнтація нижче. Щось подібне відбувається, коли ми додаємо два вектори, наприклад,

$$area(a,b + c) = area(a,b) + area(a,c)$$

знову відкладаючи питання зі знаками. Ми називаємо ці властивості лінійністю$2$ афінного об'єму. Будь-яка розумна міра m-обсягу повинна мати подібні властивості лінійності.

зміна основи

Малюнок$\PageIndex{4}$: Віола має різну площу при вимірюванні за допомогою іншого паралелограма в якості одиниці.

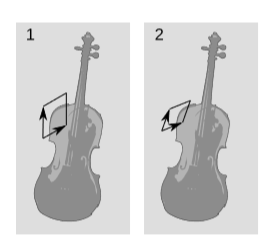
Оскільки ми досі не використовували метрику, всі наші заходи площі були відносними, а не абсолютними. Як показано на малюнку$\PageIndex{4}$, вони залежать від того, який паралелограм ми виберемо в якості нашої одиниці площі. Одинична комірка на малюнку$\PageIndex{4}$ (2) менша, ніж на малюнку$\PageIndex{1}$ (1), з двох причин: вектори, що визначають ребра, коротші, а кут між ними менший. Такі слова, як «коротше» та «кут», показують, що ми вдаємося до метричного вимірювання, але ми також могли б виконати порівняння, не використовуючи метрику, просто використовуючи паралелограм$1$ для вимірювання паралелограма$2$ або$2$ вимірювання$1$. Якщо розглядати таку пару векторів як базисні вектори для площини, то перемикання нашого вибору одиничного паралелограма еквівалентно зміні базису. Ділянки змінюються пропорційно визначнику матриці, що визначає зміну основи.

Приклад$\PageIndex{1}$: A halFLing basis

Припустимо$a' = a/2$, що, і$b' = b/2$. Зміна базису від негрунтованої пари на загрунтовану парі задається матрицею.

$$\begin{pmatrix} 2 & 0\\ 0 & 2 \end{pmatrix}$$

який має детермінант$4$. Зменшення обох базисних векторів в$2$ множник призвело до зменшення площі одиничного паралелограма$4$ в множник. Якщо використовувати загрунтований паралелограм для вимірювання інших площ, то всі площі вийдуть більше в рази$4$.

Обертання та підсилення Лоренца - це зміни основи. Вони мають детермінанти, рівні$1$, тобто зберігають об'єм простору-часу.

Орієнтація

Малюнок$\PageIndex{5}$: Лінійність площі вимагає, щоб деяким областям були присвоєні негативні значення.

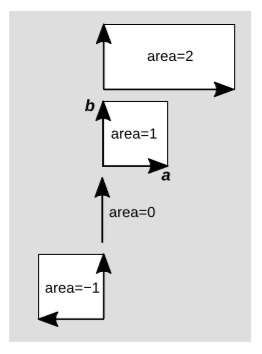
Як показано на малюнку$\PageIndex{5}$, лінійність площі вимагає, щоб деяким областям були присвоєні негативні значення. Якщо порівняти області$+1$ і$-1$, то побачимо, що єдина відмінність полягає в орієнтації, або передачі. У випадку, якому ми довільно присвоїли область$+1$, вектор b лежить проти годинникової стрілки від вектора a, але коли a перевертається, відносна орієнтація стає за годинниковою стрілкою.

Якщо у вас був звичайний першокурсник фізики, то ви бачили, що це питання розглядається певним чином, який полягає в тому, що ми припускаємо, що третій вимір існує, і визначаємо область, щоб бути векторним перехресним добутком$a×b$, який перпендикулярний площині, населеної$a$ і$b$. Біда при такому підході полягає в тому, що він працює лише в трьох вимірах. У чотирьох вимірах припустимо, що a лежить вздовж$x$ -осі, а$b$ вздовж$t$ -осі. Тоді, якщо ми повинні були визначити$a×b$, це повинно бути в напрямку, перпендикулярному обох з них, але у нас є більше одного такого напрямку. Ми могли вибрати все, що завгодно в$y-z$ літаку.

Щоб розпочати роботу з цього питання в m розмірах, де$m$ не обов'язково дорівнює$3$, можна розглянути$m$ -обсяг$m$ -мірного паралелепіпеда, охопленого$m$ векторами. Наприклад, припустимо, що в$4$ -мірному просторовічасі ми вибираємо наші$m$ вектори як одиничні вектори, що лежать уздовж чотирьох осей координат Мінковського$\hat{t},\hat{x},\hat{y}\; \text{and}\; \hat{z}$. З досвіду роботи з векторним перехресним добутком, який є антикомутативним, ми очікуємо, що знак результату буде залежати від порядку векторів, тому давайте візьмемо їх у такому порядку. Зрозуміло, що є лише два розумні значення, які ми могли собі уявити для цього обсягу:$+1$ або$-1$. Вибір довільний, тому робимо довільний вибір. Припустимо, що саме$+1$ для цього замовлення. Це означає вибір орієнтації на простору-час.

Приховане і нетривіальне припущення полягало в тому, що як тільки ми зробили цей вибір в один момент простору-часу, він може бути перенесений в інші регіони простору-часу послідовно. Це не повинно бути так, як запропоновано на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$: Смуга Мебіуса не є орієнтованою поверхнею.

Однак нашою темою на даний момент є особлива відносність, і, як коротко обговорюється в розділі 2.4, зазвичай передбачається в спеціальній теорії відносності, що просторово-час топологічно тривіальний, так що це питання виникає тільки в загальній теорії відносності, і тільки в просторовічаси, які, ймовірно, не є реалістичними моделями наш Всесвіт.

Оскільки$4$ -volume є інваріантним при обертаннях та перетвореннях Лоренца, нашого вибору орієнтації достатньо, щоб виправити визначення$4$ -обсягу, який є інваріантом Лоренца. Якщо вектори$a$$b$,$c$,, і$d$ охоплюють a$4$ -паралелепіпед, то лінійність обсягу виражається тим, що існує набір коефіцієнтів,$\epsilon _{ijkl}$ таких, що

$$V = \epsilon _{ijkl} a^i b^j c^k d^l$$

Зазначаючи це таким чином, ми інтерпретуємо його як абстрактне позначення індексу, і в цьому випадку відсутність будь-яких індексів$V$ означає, що це не просто інваріант Лоренца, але й скаляр.

Приклад$\PageIndex{2}$: HaLFLing coordinates

$(t,x,y,z)$Дозволяти координати Мінковського, і нехай$(t',x',y',z') = (2t,2x,2y,2z)$. Розглянемо, як впливає кожен з факторів у нашому рівнянні об'єму, коли ми робимо цю зміну координат.

$$\overset{\underbrace{V}}{\text{no change}}\; \; = \; \; \overset{\underbrace{\epsilon _{\kappa \lambda \mu \nu }}}{\times 1/16}\; \overset{\underbrace{a^{\kappa }}}{\times 2}\; \overset{\underbrace{b^{\lambda }}}{\times 2}\; \overset{\underbrace{c^{\mu }}}{\times 2}\; \overset{\underbrace{d^\nu }}{\times 2}$$

Оскільки наша конвенція полягає в$V$ тому, що це скаляр, він не змінюється при зміні координат. Це змушує нас говорити про те, що складові змінюються по фактору$1/16$ в цьому прикладі.

Результат Прикладу$\PageIndex{2}$ говорить нам, що згідно з нашою конвенцією цей обсяг є скаляром, компоненти повинні змінюватися, коли ми змінюємо координати. Можна стверджувати, що було б логічніше думати про трансформацію в цьому прикладі як про зміну одиниць, і в цьому випадку значення$V$ буде різним у нових одиницях; це можлива альтернативна конвенція, але вона мала б недолік унеможливлення зчитування властивості перетворення об'єкта від числа і положення його індексів. Згідно з нашою конвенцією, ми можемо таким чином зчитувати властивості трансформації. Хоча розділ 7.4 представив ці властивості лише у випадку тензорів рангу$0$ і$1$, відклавши загальний опис тензорів вищого рангу до розділу 9.2, властивості перетворення є, як$\epsilon$ це передбачено чотирма його індексами, властивостями тензора рангу $4$. Різні автори використовують різні умовності щодо визначення$\epsilon$, яке спочатку було описано математиком Леві-Чівіта.

Малюнок$\PageIndex{7}$: Тулліо Леві-Чівіта (1873-1941) працював над моделями систем числення, що володіють нескінченними величинами, і над диференціальною геометрією. Він винайшов тензорні позначення, які Ейнштейн дізнався зі свого підручника. Він був призначений на престижні наділені кафедри в Падуї та Римському університеті, але був звільнений у 1938 році, оскільки він був євреєм і антифашистом.

Оскільки за нашою умовністю$\epsilon$ є тензором, ми називаємо його тензором Леві-Чивіта. В інших конвенціях, де$\epsilon$ не тензор, його можна назвати символом Леві-Чівіта. Оскільки позначення не стандартизовані, я іноді ставлю нагадування поруч із важливими рівняннями, що$\epsilon$ містять твердження, що це тензоріал$\epsilon$.

Тензор Levi-Civita має багато і багато індексів. Страшно! Уявіть собі складність цього звіра. (Риб.) У нас є чотири варіанти для першого індексу, чотири для другого, і так далі, так що загальна кількість компонентів є$256$. Зачекайте, не дотягуйтеся до kleenex. Наступний приклад показує, що ця складність є ілюзорною.

Приклад$\PageIndex{3}$: Volume in Minkowski coordinates

Ми створили наші визначення так, що для паралелепіпеда$\hat{t},\hat{x},\hat{y},\hat{z}$, ми маємо$V = +1$. Тому

$$\epsilon _{txyz} = +1$$

за визначенням, і оскільки$4$ -volume є інваріантним Лоренцем, це стосується будь-якого набору координат Мінковського.

Якщо$x$ помінятися і$y$ скласти список$\hat{t},\hat{y},\hat{x},\hat{z}$, то як на малюнку$\PageIndex{5}$ обсяг стає$-1$, так

$$\epsilon _{tyxz} = -1$$

Припустимо, ми беремо краю нашого паралелепіпеда бути$\hat{t},\hat{x},\hat{x},\hat{z}$, з$y$ опущеними і$x$ дубльованими. Ці чотири вектори не лінійно незалежні, тому наш паралелепіпед вироджений і має нульовий обсяг.

$$\epsilon _{txxz} = 0$$

З цих прикладів ми бачимо, що як тільки будь-який елемент був зафіксований, всі інші також можуть бути визначені. Правило полягає в тому, що обмін будь-якими двома індексами перевертає знак, а будь-який повторюваний індекс робить результат нулем.

Приклад$\PageIndex{3}$ показує, що вигадливий символ$\epsilon _{ijkl}$, який виглядає як таємний ієрогліф майя, що викликає$256$ різні числа, насправді кодує інформацію лише одного числа; кожен компонент тензора або дорівнює цьому числу, або мінус це число, або нуль. Припустимо, ми працюємо в деякому наборі координат, який може бути не Мінковський, і ми хочемо знайти це число. Складним способом знайти це було б використання закону тензорного перетворення для$4$ ранг-тензора (розділ 9.2). Набагато простішим способом є використання визначника метрики, розглянутого в прикладі 6.2.1. Для списку координат ijkl, які відсортовані в порядку, який ми визначаємо як позитивну орієнтацію, результат просто$\epsilon _{ijkl} = \sqrt{\left | det\; g \right |}$. Знак абсолютного значення потрібен тому, що релятивістська метрика має негативний детермінант.

Приклад$\PageIndex{4}$: Cartesian coordinates and their halFLIng versions

Розглянемо евклідові координати в площині, щоб метрика була$2×2$ матрицею, і$\epsilon _{ij}$ мала всього два індекси. У стандартних декартових координатах метрика є$g = diag(1,1)$, яка має$det\; g = 1$. Таким чином, тензор Леві-Чівіта має$\epsilon _{xy} = +1\]), and its other three components are uniquely determined from this one by the rules discussed in Example \(\PageIndex{3}$. (Ми могли б перевернути всі знаки, якби хотіли вибрати протилежну орієнтацію для площини.) У матричній формі ці правила призводять до

$$\epsilon = \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}$$

Тепер трансформуємо в координати$(x',y') = (2x,2y)$. У цих координатах метрика$g' = diag(1/4,1/4)$, з$det\; g = 1/16$, так що$\epsilon _{x'y'} = 1/4$, або в матричній формі,

$$\epsilon '= \begin{pmatrix} 0 & 1/4\\ -1/4 & 0 \end{pmatrix}$$

Приклад$\PageIndex{5}$: Polar coordinates

У полярних$(r,θ)$ координатах метрика є$g = diag(1,r^2)$, яка має детермінант$r^2$. Тензор Леві-Чівіта є

$$\epsilon = \begin{pmatrix} 0 & r\\ -r & 0 \end{pmatrix}$$

(беручи ту ж орієнтацію, що і в прикладі$\PageIndex{4}$).

Приклад$\PageIndex{6}$: Area of a circle

Знайдемо площу одиничного кола. Його (підписана) площа

$$A = \int \text{2-volume}(dr, d\theta )$$

де порядок$dr$ і$dθ$ вибирається так, що з орієнтацією, яку ми використовували для площини, результат вийде позитивним. Використовуючи визначення тензора Леві-Чивіта, ми маємо

$$\begin{align*} A &= \int \epsilon _{r\theta } dx^r dx^\theta \\ &= \int_{r = 0}^{1}\int_{\theta =0}^{2\pi }rdrd\theta \\ &= \pi \end{align*}$$

3-об'ємний ковектор

Розглянемо обсяг тривимірного підпростору чотиривимірного просторучасу. Лінійність призводить до особливо простої характеристики$3$ -обсягу. Нехай$3$ -volume визначається паралелепіпедом, що охоплюється векторами$a$$b$, і$c$. Якби ми кинули четвертий вектор$d$, у нас був би$4$ -volume, а$4$ -volume - скаляр. Цей$4$ -обсяг буде залежати лінійно від усіх чотирьох векторів, і, зокрема, він буде залежати лінійно від$d$. Але це означає, що у нас є скаляр, який є лінійною функцією вектора, і така функція саме те, що ми маємо на увазі під ковектором. Тому ми можемо визначити об'ємний ковектор$S$ відповідно до

$$S_l d^l = \text{4-volume(a,b,c,d)}$$

або

$$S_l = \epsilon _{ijkl} a^i b^j c^k \; \; \; \; [\text{tensorial }\epsilon ]$$

Малюнок$\PageIndex{8}$: Інтерпретація 3-об'ємного ковектора.

Об'ємний ковектор збирає інформацію про обсяг$3$ -паралелепіпеда, інкапсулюючи його в зручній формі з відомими властивостями перетворення. Зокрема, твердження і доказ теореми Гаусса в$3 + 1$ розмірах значно спрощуються за рахунок використання цього інструменту. Ковектор$3$ -обсяг, на відміну від афінного$3$ -обсягу, визначається в абсолютному сенсі, а не по відношенню до якогось паралелепіпеда, довільно обраного в якості стандарту. І ковектор, і афінний об'єм не задовольняють властивість порівняння коефіцієнтів V1, оскільки ми не можемо порівнювати обсяги, якщо вони не лежать в паралельних$3$ площинам.

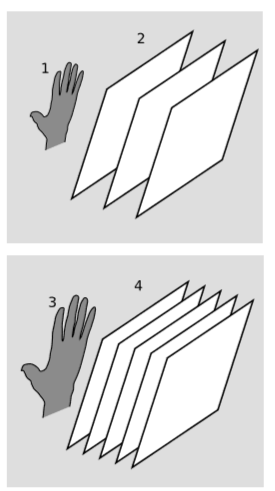
Ми візуалізуємо ковектори в$n$ розмірах у вигляді штабелів$(n-1)$ розмірних площин (рис. 6.3.1; рис. 6.6.1). Тому об'ємний тривимірний вектор повинен бути візуалізований як стек$3$ -площин у чотиривимірному просторі. Оскільки більшість з нас не може візуалізувати речі дуже добре в чотирьох вимірах, фігура$\PageIndex{8}$ опускає один з розмірів, так що$3$ -поверхні виглядають як двовимірні площини. Малий фігурка руки $\PageIndex{1}$(1) має певний$3$ -обсяг, а ковектор, який її вимірює, представлений стеком$3$ -площин, паралельних їй, малюнок $\PageIndex{1}$(2). Більша фігура руки $\PageIndex{1}$(3) має вдвічі більший$3$ об'єм, а її ковектор представлений стопкою площин з половиною відстані.

Якщо відступити від чотирьох вимірів до трьох, то об'ємний ковектор утворений векторами$u$ і$v$ стає векторним перехресним добутком$S = u×v$, т. Е$S_k = \epsilon _{ijk} u^i v^j$.

Приклад$\PageIndex{7}$: A vector cross product

Розглянемо евклідовий 3-простір у декартових координатах. З фізики першокурсника ми знаємо, що

$$\hat{z} = \hat{x}\times \hat{y}$$

Перевиражаючи це в позначеннях вище$u^x = 1$, ми маємо$v^y = 1$, і нуль для всіх інших компонентів$u$ і$v$. Оскільки тензор Levi-Civita зникає, якщо у нас є якісь дубльовані індекси, його єдиний незникаючий компонент, який може бути актуальним тут$\epsilon _{xyz}= 1$. (Тут ми припускаємо стандартну правосторонню орієнтацію для декартових координат, і ми використовуємо той факт$g = diag(1,1,1)$, що, так що$detg = 1$.) Результат -

$$S_z = \epsilon _{xyz}u^x v^x = 1$$

як очікувалося. (Тут не має значення, чи ми говоримо про$S_z$ або$S^z$, тому що за допомогою цієї метрики підвищення та зниження індексів не змінює компоненти вектора.)

Класифікація 3-поверхонь

Корисним застосуванням ковектора$3$ -об'єму є класифікація$3$ -поверхонь за тим, як вони відносяться до світлового конуса. Якщо прибити три палички, всі під прямим кутом один до одного, то я можу розглядати їх як набір базисних векторів, що охоплюють тривимірний простір подій. Цей трипростір плоский, тому ми можемо назвати його гіперплощиною - або просто площиною, якщо, як і в цьому розділі, немає небезпеки забути, що він має три виміри, а не два. Всі події в цій площині є одночасними в моїй системі відліку. Жоден з цих фактів не залежить від використання прямих кутів; нам просто потрібно переконатися, що палички не всі лежать в одній площині.

Справа фізика полягає в тому, щоб в кінцевому рахунку робити прогнози. Тобто, якщо дати набір початкових умов, ми можемо сказати, як наша система буде розвиватися через час. Ці початкові умови в принципі вимірюються по всьому простору, і площина одночасності буде природним вибором для множини точок, в яких слід проводити вимірювання. Поверхня, яка використовується для цієї мети, називається поверхнею Коші.

Якщо площина є поверхнею одночасності на думку якогось спостерігача, то ми називаємо її космічною. Світова лінія будь-якої частинки повинна перетинати таку площину рівно один раз, і саме тому вона працює як поверхня Коші: ми гарантовано виявляємо частинку, щоб ми могли врахувати її вплив на еволюцію космосу. Ми могли б взяти космічний літак і переорієнтувати його. Для досить невеликої зміни орієнтації (тобто зміни, яку можна було б описати досить невеликими змінами базових векторів), вона залишиться схожою на простір.

Коли площина не схожа на простір і залишається такою при будь-якій досить невеликій зміні орієнтації, ми називаємо це timeslike. У координатах Мінковського прикладом може бути$t-x-y$ літак. Світова лінія даної частинки ніколи не може перетнути таку поверхню, і тому подібну до часу площину не можна використовувати як поверхню Коші.

Літак, який не є ні космічним, ні схожим на час, називається світлоподібним. Прикладом може служити поверхня, визначена рівнянням$x = t$ в координатах Мінковського.

Вищевказану класифікацію можна висловити дуже стисло, використовуючи ковектор$3$ -об'єм, визначений вище. Площина є космічною, світлоподібною або схожою на час, відповідно, якщо регіони, які вона містить, описуються ковекторами$3$ -об'ємом, які є часовими, світлоподібними або космічними. Поверхня, яка є гладкою, але не обов'язково плоскою, може бути описана локально відповідно до цих категорій, враховуючи її дотичну площину. Наприклад, світловий конус є світлоподібним у кожній його точці, і оскільки він скрізь світлий, ми називаємо його світлоподібною поверхнею. Горизонт подій чорної діри також є світлоподібною поверхнею. Будь-яка космічна поверхня, вигнута або плоска, може бути використана як поверхня Коші.

Світлоподібні поверхні мають деякі кумедні властивості. Використовуючи позначення birdtracks, припустимо, що ми формуємо таку поверхню, як простір, що охоплюється трьома базисними векторами$\to a$$\to b$$\to c$, і, і нехай$S \to$ буде відповідний$3$ -об'ємний ковектор. Поверхня світлоподібна, тому

$$S \to S = 0$$

Тому що$S \to$ визначається як функція, що дає$4$ -обсяг паралелепіпеда, що охоплюється основами з четвертим вектором$\to d$, і оскільки цей обсяг$\to d$ зникає, коли дотична до поверхні (властивість V2), ми маємо,

$$S \to a = S \to b = S \to c = 0$$

Так що в цьому$S \to$ сенсі перпендикулярно поверхні. У евклідовому просторі ми звикли описувати орієнтацію поверхні з точки зору одиничного нормального вектора, і це майже те, що$S \to$ є, за винятком того, що це ковектор, а не вектор, і він також не може бути змушений мати одиничну довжину, оскільки його величина дорівнює нулю. Ми могли б виправити першу з цих двох проблем, побудувавши вектор,$\to S$ який є подвійним$S\to$, але це має збентежений ефект. Поєднуючись$\PageIndex{17}$ з визначенням$S\to$, ми виявляємо, що$\to S$ охоплює зникаючий$4$ -обсяг з базисними векторами, і тому по V2 ми знаходимо, що$\to S$ дотична до поверхні. Таким чином, у певному сенсі ми маємо вектор, який є паралельним і дотичним до поверхні, що дозволяє уникнути абсурду, оскільки ми дійсно маємо на увазі два різні об'єкти, ковектор$S\to$ і вектор$\to S$.