7.3: Перетворення метрики
- Page ID
- 77224
Цілі навчання
- Поясніть перетворення метрики при зміні координат Мінковського
Продовжуючи приклад прискорених координат, давайте знайдемо, що відбувається з метрикою, коли ми змінюємо координати Мінковського. Координати Мінковського по суті визначаються так, що метрика має звичну форму з коефіцієнтами\(+1\) і\(-1\). У відносності часто представляють метрику, показуючи її результат при застосуванні до нескінченно малого зміщення\((dt,dx)\):
\[ds^2 = dt^2 - dx^2\]
Тут\(ds\) би представляли належний час, в тому випадку, коли зміщення було схожим на час. Оскільки ми вже визначили, що
\[dt = X \cosh T dT + \sinh T dX\]
і
\[dx = X \sinh T dT + \cosh T dX\]
ми можемо просто підставити в вираз для ds, щоб знайти форму метрики в\((T,X)\) координатах. Використовуючи особистість\(\cosh ^2 - \sinh ^2 = 1\), знаходимо
\[ds^2 = X^2 dT^2 - dX^2\]
Змінне значення\(dT^2\) коефіцієнта насправді є саме таким ефектом розширення гравітаційного часу, існування якого ми передбачили в розділі 5.2 на основі принципу еквівалентності. Форма метрики виведена була
\[ds^2 ≈ (1 + 2∆Φ) dT^2 - dX^2\]
де\(∆Φ\) - різниця гравітаційного потенціалу щодо деякої опорної висоти. Одним із використовуваних наближень було припущення, що діапазон висот\(X\) був невеликим, але з урахуванням цього наближення два результати повинні погодитися. Для зручності розглянемо спостерігачів в тому регіоні\(X ≈ 1\), де прискорення приблизно\(1\). Тоді\(∆Φ = Φ(1 + ∆X) - Φ(1) ≈ \text{(acceleration)(height)} ≈ X\), так коефіцієнт часу в другій формі метрики дорівнює\(≈ 1+2∆Φ ≈ 1+2∆X\). Але щоб в межах бажаного рівня наближення, це те ж саме, що\(X^2 = (1+∆X)^2 ≈ 1 + 2∆X\).
Процедура, застосована вище, працює в цілому. Для перетворення метрики з координат\((t,x,y,z)\) в нові\((t',x',y',z')\) координати отримуємо негрунтовані координати в терміні загрунтованих, беремо диференціали з обох сторін і усуваємо на користь\(t, ..., dt, ...\)\(t', ...dt', ...\) в виразі for\(ds^2\). У розділі 9.2 ми побачимо, що це приклад більш загального закону перетворення для тензорів, математичних об'єктів, які узагальнюють вектори та ковектори так само, як матриці узагальнюють вектори рядків і стовпців. Скаляр, без індексів, називається тензором рангу\(0\). Вектори і ковектори, що мають один індекс, називаються ранг-\(1\) тензорами.
Приклад\(\PageIndex{1}\): A map projection
Оскільки земна поверхня вигнута, неможливо зобразити її на плоскій карті без спотворень. \(φ\)Дозволяти широта, θ кут, виміряний вниз від північного полюса (відомий як широта), обидва вимірюються в радіанах, і нехай a буде радіус землі. Тоді за визначенням радіанової міри нескінченно мале зміщення північ-південь на\(dθ\) відстань\(adθ\). Точка на заданій широті\(θ\) лежить на відстані\(a \sinθ\) від осі, тому для нескінченно малої відстані схід-захід ми маємо\(a \sin θ dφ\). Для зручності нехай агрегати будуть обрані такі, що\(a = 1\). Тоді метрика, з підписом\(++\), є
\[ds^2 = dθ^2 +\sin^2 θ dφ\]
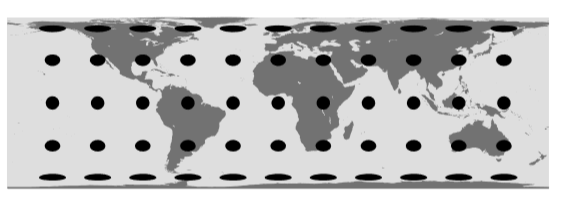
Одним з багатьох можливих способів формування плоскої карти є циліндрична проекція Ламберта,
\[x = φ\]
\[y = \cosθ\]
показано на малюнку\(\PageIndex{1}\). Якщо ми бачимо відстань на карті і хочемо знати, наскільки вона насправді знаходиться на земній поверхні, нам потрібно
перетворити метрику в\((x,y)\) координати. Обернене перетворення координат дорівнює
\[φ = x\]
\[θ = \cos^{-1} y\]
Беручи диференціали з обох сторін, отримуємо
\[dφ = dx\]
\[d\theta = -\dfrac{dy}{\sqrt{1-y^2}}\]
Беремо метрику і усуваємо\(θ\),\(φ\),\(dθ\), і\(dφ\), знаходячи
\[ds^2 = (1 - y^2)dx^2 + \dfrac{1}{1 - y^2}dy^2\]
На малюнку\(\PageIndex{1}\) візерунок в горошок складається з фігур, які насправді є колами, всі однакового розміру, на земній поверхні. Оскільки вони досить малі, ми можемо наблизити\(y\) як мають одне значення для кожного кола, а це означає, що вони представлені на плоскій карті як приблизні еліпси з їх розмірами схід-захід розтягнуті на,\((1 - y^2)^{-1/2}\) а їх північ-південь зменшені\((1 - y^2)^{1/2}\). Оскільки ці два фактори зворотні один одному, площа кожного еліпса така ж, як і площа вихідного кола, і тому така ж, як і у всіх інших еліпсів. Вони є візуальним зображенням метрики, і вони демонструють рівноплову властивість цієї проекції.