7.2: Трансформація векторів

Цілі навчання

• Поясніть, як трансформувати вектори

Тепер припустимо, ми хочемо перетворити вектор, компоненти якого виражаються в$(T,X)$ координатах в компоненти, виражені в$(t,x)$.

Малюнок$\PageIndex{1}$: Перетворення між координатами Мінковського$(t,x)$ та прискореними координатами$(T,X)$

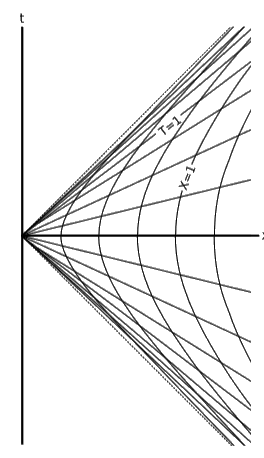
Нашим найпростішим прикладом вектора є зміщення$(∆T,∆X)$, і якщо ми зробимо це нескінченно малим,$(dT,dX)$ то нам не потрібно турбуватися про те, що діаграма на малюнку$\PageIndex{1}$ має криві - крупним планом криві виглядають як прямі лінії. ¹ Якщо ми думаємо про координату$t$ як функцію двох змінних$t = t(T,X)$,$t$ то змінюється з двох різних причин:$T$ змінюється її перший вхід, а також другий вхід$X$. $t$Якби була лише функція однієї змінної$t(T)$, то зміна в$t$ було б дано просто правилом ланцюга,$dT = \frac{dt/dT}{d} T$. Оскільки він насправді має дві такі причини для зміни, ми додаємо дві зміни:

$$dt = \frac{\partial t}{\partial T} dT + \frac{\partial t}{\partial X} dX$$

Похідні є частковими похідними, і ці похідні існують, оскільки, як ми завжди будемо вважати, зміна координат плавна. Точно аналогічний вираз застосовується для$dx$.

$$dx = \frac{\partial x}{\partial T} dT + \frac{\partial x}{\partial X} dX$$

Перш ніж провести подробиці цього розрахунку, зупинимося і відзначимо, що результати поки повністю загальні. Оскільки ми досі не використовували фактичні рівняння для цієї конкретної зміни координат, ці вирази застосовуватимуться до будь-якого такого перетворення, включаючи особливі випадки, з якими ми стикалися досі, такі як перетворення Лоренца та масштабування. (Наприклад, якби ми масштабували за коефіцієнтом$α$, то всі часткові похідні просто дорівнювали б$α$.). Крім того, наше визначення вектора полягає в тому, що вектор - це все, що перетворюється як вектор. Оскільки ми встановили, що наведені вище правила застосовуються до вектора зміщення, ми робимо висновок, що вони також застосовуватимуться до будь-якого іншого вектора, скажімо, вектору енергії-імпульсу.

Повертаючись до цього конкретного прикладу, застосування фактів

$$\frac{\mathrm{d} \sinh u}{\mathrm{d} u} = \cosh u\; \; \text{and}\; \; \frac{\mathrm{d} \cosh u}{\mathrm{d} u} = \sinh u$$

говорить нам, що вектор$(dT,dX)$ перетворюється на:

$$(dt,dx) = (X \cosh T dT + \sinh T dX ,\; X \sinh T dT + \cosh T dX)$$

Як приклад того, як це універсально застосовується до будь-якого типу вектора, припустимо, що спостерігач на борту космічного корабля зі світовою лінією$(T,X) = (τ,1)$ має улюблене прес-пап'є з масою$m$. Згідно з вимірами, проведеними на борту її корабля, його енергетично-імпульсний вектор становить:

$$(p_T,p_X) = (m,0)$$

У неприскореному координатах це стає

$$\begin{align*} (p_t,p_x) &= (X \cosh T p_T + \sinh T p_X ,\; X \sinh T p_T + \cosh T p_X)\\ &= (mX\cosh T,\; mX\sinh T)\\ &= (m\cosh \tau ,\; m\sinh \tau ) \end{align*}$$

Оскільки функції cosh і sinh поводяться як$e^x$ для великих$x$, ми виявляємо, що після того, як космонавт витратив розумну кількість належного часу на$τ$ прискорення, масова енергія та імпульс прес-пап'є виростуть до того моменту, коли це дивовижна зброя масового знищення, здатна знищення цілої галактики.

Посилання

¹ Тут ми використовуємо той факт, що зміна координат була плавною, тобто дифеоморфізм. Інакше криві можуть мати перегини в них, які все одно виглядали б як перегини при будь-якому збільшенні.