4.4: Системи з внутрішньою структурою

Last updated
Save as PDF

Page ID: 77287

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначити, чи\(E = mc^2\) має оригінальний доказ Ейнштейна логічні недоліки
Також визначте, чи дійсний заявлений результат лише за певних умов

Розділ 4.2 представив по суті оригінальний доказ Ейнштейна\(E = mc^2\), який піддавався критиці з кількох підстав. Детальну дискусію дає Оганян. ¹ Відклавши в сторону питання, які є чисто історичними або стосуються лише академічного пріоритету, ми хотіли б знати, чи є доказ логічні недоліки, а також чи є заявлений результат дійсним лише за певних умов. Потрібно розглянути наступні питання:

Чи має значення, чи описувана система має кінцеву просторову протяжність, чи система ізольована?
Чи має значення, чи рухаються частини системи з релятивістськими швидкостями?
Чи має значення низькошвидкісне наближення, яке використовується в доказах Ейнштейна?
Як ми обробляємо систему, яка не складається з точкових частинок, наприклад, конденсатора, в якому частина енергії-імпульсу знаходиться в електричному полі?

Наступний приклад демонструє проблеми 1-3 та їх логічні зв'язки; дефініційне питання 4 розглядається в главі 9.

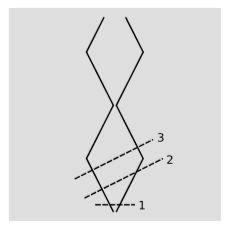
рис 4.4.1.png — Малюнок\(\PageIndex{1}\): Світові лінії з двох намистин, що підстрибують вперед-назад на дроті.

Припустимо, що дві намистини вільно ковзають на дроті, пружно відскакуючи один від одного, а також пружно відскакуючи від кінців дроту. Їх світові лінії показані на малюнку\(\PageIndex{1}\). Припустимо, бісер кожен має одиницю маси. У\(o\) рамці намистини звільняються від центру дроту зі швидкостями\(±u\). Для конкретності поставимо\(u = 1/2\), щоб система мала внутрішній рух на релятивістських швидкостях. У цьому кадрі сумарний вектор енергії-імпульсу системи, на поверхні одночасності, позначеної на\(1\) малюнку\(\PageIndex{1}\), є\(p = (2.31,0)\). Тобто він має загальну масову енергію\(2.31\) одиниць, і сумарний імпульс нуль (мається на увазі, що це центр маси кадру). З плином часу спостерігач в цьому кадрі скаже, що кульки досягають кінців дроту одночасно, і в цей момент вони відскакують, зберігаючи той же сумарний вектор енергії-імпульсу\(p\). Маса системи - це, за визначенням,

\[m = \sqrt{p_{t}^{2} - p_{x}^{2}} = \sqrt{2.31}\]

і ця маса залишається постійною, оскільки кульки відскакують вперед і назад. Тепер давайте перетворимося на кадр\(o'\), рухаючись зі швидкістю\(v = 1/2\) відносно\(o\). Якщо швидкості додаються лінійно в відносності, то початкові швидкості бісеру в цьому кадрі будуть\(0\) і\(-1\), але, звичайно, матеріальний об'єкт не може рухатися зі швидкістю\(|v| = c = 1\), а швидкості не додаються лінійно. Застосовуючи правильну формулу додавання швидкості для відносності, ми виявимо, що кульки мають початкові швидкості\(0\) і\(-0.8\) в цьому кадрі, і якщо обчислити їх сумарний вектор енергії-імпульсу, то на поверхні одночасності на\(2\) малюнку\(\PageIndex{1}\) ми отримаємо\(p' = (2.67,-1.33)\). Це саме те, що ми отримали б, взявши оригінальний вектор\(p\) і просунувши його через перетворення Лоренца. Тобто, вектор енергії-імпульсу, здається, діє як хороший чотиривекторний, хоча система має кінцеву просторову ступінь і містить частини, які рухаються з релятивістськими швидкостями. Зокрема, це означає, що система має таку ж масу,\(m = \sqrt{2.31}\) як і в\(o\), оскільки\(m\) є нормою\(p\) вектора, а норма вектора залишається однаковою при перетворенні Лоренца.

Але тепер розглянемо поверхню\(3\), яку,\(2\) начебто, спостерігач\(o'\) вважає поверхнею одночасності. В цей час\(o'\) говорить про те, що обидві намистини рухаються вліво. Між часом\(2\) і часом\(o'\) говорить про те\(3\), що загальний імпульс системи змінився, тоді як її загальна масова енергія залишалася постійною. Його маса різна, і сумарний вектор енергії-імпульсу\(p'\) в часі не\(3\) пов'язаний перетворенням Лоренца зі значенням в\(p\) будь-який час кадру\(o\). Причина такої неправильної поведінки полягає в тому, що права намистина відскочила від правого кінця дроту, але тому, що\(o\) і\(o'\) мають різні думки щодо одночасності,\(o'\) говорить, що ще не було жодного відповідного зіткнення для бісеру зліва.

Але всі ці труднощі виникають тільки тому, що ми щось залишили поза увагою. Коли права намистина відскакує від правого кінця дроту, це зіткнення між намистиною і дротом. Після зіткнення провід відскакує вправо (або в ньому створюється вібрація). Ігноруючи відскік дроту, ми порушили закон збереження імпульсу. Якщо брати до уваги імпульс, наданий проводу, то вектор енергії-імпульсу всієї системи зберігається, і тому повинен бути однаковим при\(2\) і\(3\).

Підсумок всього цього полягає в тому, що\(E = mc^2\) і чотиривекторний характер обидва\(p\) дійсні для систем з скінченною просторовою протяжністю, за умови, що системи ізольовані. «Ізольований» означає просто те, що ми не повинні безоплатно ігнорувати щось таке, як провід у цьому прикладі, який обмінюється енергією імпульсу з нашою системою. Щоб навести загальний доказ цього, корисно буде розробити ідею тензора стрес-енергії (розділ 9.2), який дозволяє стисло констатацію того, що ми маємо на увазі під збереженням енергії-імпульсу. Доказ наведено в розділі 9.3.

Посилання

¹ «\(E = mc^2\)Помилки Ейнштейна», arxiv.org/abs/0805.1400