4.2: Е = мК²

Цілі навчання

• Релятивістська теорія гравітації і\(E = mc^2\) пояснюється

Тепер ми знаємо релятивістський вираз для кінетичної енергії в граничному випадку ультрарелятивістської частинки: її енергія пропорційна «фактору розтягування»\(D\) перетворення Лоренца. Як щодо проміжних випадків, як\(v = c/2\)?

Малюнок\(\PageIndex{1}\): Сірник запалюється всередині баночки дзвінка. Він горить, і енергія виривається з баночки у вигляді світла. Після того як він перестане горіти, все ті ж атоми все одно знаходяться в баночці: ніхто не увійшов і не втік. На малюнку показаний результат, очікуваний до відносності, який полягав у тому, що маса, виміряна на балансі, залишиться точно такою ж. Це не те, що відбувається насправді.

Коли ми змушені возитися з перевіреною часом теорією, нашим першим інстинктом завжди слід возитися якомога консервативно. Хоча ми були змушені визнати, що кінетична енергія не змінюється, як\(v^2/2\) при релятивістських швидкостях, наступна найбільш консервативна річ, яку ми могли б зробити, - це припустити, що єдина необхідна зміна - замінити фактор нерелятивістського\(v^2/2\) вираження кінетичної енергії деякими іншими. функція, яка повинна була б діяти як\(D\) або\(1/D\) для\(v \rightarrow \pm c\). Я підозрюю, що це те, що думав Ейнштейн, коли він завершив свою оригінальну роботу про відносність у 1905 році, тому що пізніше того ж року він опублікував другий документ, який показує, що цього все ще недостатньо змін для створення робочої теорії. Тепер ми знаємо, що є щось більше, що потрібно змінити щодо пререлятивістської фізики, і це припущення, що маса - це лише властивість матеріальних частинок, таких як атоми (малюнок\(\PageIndex{1}\)). Називайте це «гіпотезою лише атомів».

Тепер, коли ми знаємо правильний релятивістський спосіб знаходження енергії променя світла, виявляється, що ми можемо використовувати її, щоб знайти те, що шукали спочатку, а це була енергія матеріального об'єкта. Наступна дискусія уважно стежить за Ейнштейном.

Припустимо, що\(O\) матеріальний об'єкт маси\(m_o\), спочатку перебуваючи в спокої в певному кадрі\(A\), випромінює два промені світла (або будь-який інший вид ультрарелятивістських частинок), кожен з яких має енергію\(E/2\). За рахунок збереження енергії об'єкт повинен втратити кількість енергії, рівне\(E\). За симетрії\(O\) залишається в стані спокою.

Тепер ми переходимо на інший кадр відліку, що\(B\) рухається з деякою довільною швидкістю, що відповідає коефіцієнту розтягування\(D\). Зміна кадрів означає, що ми переслідуємо один промінь, так що його енергія зменшується до\(\left ( \frac{E}{2} \right )D^{-1}\), тікаючи від іншого, чия енергія збільшується до\(\left ( \frac{E}{2} \right )D\). У кадрі\(B\), як і в\(A\),\(O\) зберігає таку ж швидкість після випромінювання світла. Але спостерігачі в кадрах\(A\) і\(B\) розходяться в думках про те, скільки енергії\(O\) втратила, невідповідність бути

\[E\left [ \frac{1}{2} (D + D^{-1})-1\right ]\]

Це можна переписати за допомогою ідентифікатора [2] з розділу 3.6 як

\[E(\gamma -1)\]

Розглянемо випадок, коли швидкість B відносно A мала. Використовуючи наближення\(\gamma \approx 1 + \frac{v^2}{2}\), наш результат приблизно

\[\frac{1}{2}Ev^2\]

нехтуючи умовами замовлення\(v^4\) і вище. Тлумачення полягає\(E\) в тому, що при\(O\) зниженні його енергії, щоб зробити світлові промені, він зменшував свою масу від\(m_o\)\(m_o - m\) туди, де\(m = E\). Вставляючи необхідний фактор,\(c^2\) щоб зробити це дійсним у одиницях\(c \neq 1\), де ми маємо знаменитий Ейнштейн

\[E = mc^2\]

Це виведення спричинило за собою як наближення, так і деякі приховані припущення. Ці питання більш детально розглянуті в розділі 4.4. Результат виявляється справедливим для будь-якого ізольованого тіла.

Ми виявляємо, що маса - це не просто вбудована властивість частинок, що складають об'єкт, причому маса об'єкта є сумою мас його частинок. Швидше, маса і енергія рівнозначні, так що якщо експеримент по фігурі а провести з досить точним балансом, показання впадуть через масового еквівалента енергії, що випромінюється у вигляді світла.

Рівняння\(E = mc^2\) говорить нам, скільки енергії еквівалентно скільки маси: коефіцієнт перетворення - квадрат швидкості світла,\(c\). Оскільки\(c\) велике число, ви отримуєте дійсно велике число, коли ви помножите його сам по собі, щоб отримати\(c^2\). Це означає, що навіть невелика кількість маси еквівалентно дуже великій кількості енергії. І навпаки, звичайна кількість енергії відповідає надзвичайно малій масі, і саме тому ніхто не виявив ненульового результату експериментів, як той, який був на малюнку\(\PageIndex{1}\) сотні років тому.

Великою подією тут є еквівалентність маси енергії, але ми також можемо отримати результат для енергії матеріальної частинки, що рухається з певною швидкістю. Ми маємо\(m(γ - 1)\) для різниці між\(O\) енергією в кадрі\(B\) та її енергією, коли вона знаходиться в стані спокою, тобто її кінетичною енергією. Але оскільки маса і енергія еквівалентні, ми\(O\) призначаємо енергію m, коли вона знаходиться в стані спокою. Результатом є те, що енергія

\[E = m\gamma\]

(Або\(mγc^2\) в одиницях с\(c \neq 1\)).

Приклад\(\PageIndex{1}\): Electron-positron annihilation

Природна радіоактивність в землі виробляє позитрони, які схожі на електрони, але мають протилежний заряд. Форма антиречовини, позитрони анігілюють електронами для отримання гамма-променів, форма високочастотного світла. Такий процес вважався б неможливим до Ейнштейна, оскільки збереження маси та енергії вважалося окремими принципами, і цей процес усуває\(100\%\) початкову масу. Кількість енергії, виробленої при знищенні речовини\(1\: kg\) з\(1\: kg\) антиречовиною, становить

\[\begin{align*} E&= mc^2\\ &= (2\: kg)\left ( 3.0 \times 10^8 m/s^2\right )^2 \\ &= 2 \times 10^{17}\: J \end{align*}\]

який знаходиться на тому ж порядку, що і денне споживання енергії для всього населення планети!

Позитронна анігіляція є основою для медичної методики візуалізації, яка називається ПЕТ (позитронно-емісійна томографія) сканування, при якій пацієнту вводять позитрон випромінюють хімічну речовину і відображається випромінюванням гамма-променів з частин тіла, де він накопичується.

Малюнок\(\PageIndex{2}\): Верх: ПЕТ-сканер. Середина: Кожен позитрон анігілює електроном, виробляючи два гамма-промені, які відлітають спиною до спини. Коли два гамма-промені спостерігаються одночасно в кільці детекторів, передбачається, що вони походять від одного і того ж події анігіляції, і точка, в якій вони були випущені, повинна лежати на лінії, що з'єднує два детектори. Внизу: Сканування тулуба людини. Організм сконцентрував радіоактивний трактор навколо шлунка, що свідчить про ненормальний медичний стан.

Приклад\(\PageIndex{2}\): A rusting nail

Залізний цвях залишають в чашці з водою, поки він повністю не перетвориться на іржу. Енергія, що виділяється - це приблизно\(0.5\: MJ\). Теоретично, чи буде досить точна шкала реєструвати зміну маси? Якщо так, то скільки?

Рішення

Енергія буде з'являтися у вигляді тепла, яке буде втрачено навколишньому середовищу. Загальна масова енергія чашки, води та заліза дійсно буде зменшена\(0.5\: MJ\). (Якби він був ідеально ізольований, змін не було б, оскільки теплова енергія потрапила б у чашку.) Швидкість світла є\(c = 3×10^8\: m/s\), тому перетворення в одиниці маси, ми маємо

\[\begin{align*} m&= \frac{E}{c^2}\\ &= \frac{0.5 \times 10^6\: J}{(3 \times 10^8\: m/s)^2}\\ &= 6 \times 10^{-12}\: kg \end{align*}\]

Зміна маси занадто мала, щоб виміряти будь-якою практичною технікою. Це пояснюється тим, що квадрата швидкості світла така велика кількість.

Приклад\(\PageIndex{3}\): Relativistic kinetic energy

Приблизно до 1930 року прискорювачі частинок прогресували до того моменту, коли регулярно враховувалися релятивістські ефекти. У 1964 р. Бертоцці зробив спеціальний експеримент для перевірки прогнозів відносності за допомогою прискорювача електронів. Результати були розглянуті менш детально в прикладі 3.3.1, в цей момент ми ще не бачили релятивістського рівняння для кінетичної енергії. Електрони були прискорені через статичну різницю електричних потенціалів\(V\) до різних кінетичних енергій\(K = eV\), а їх швидкості виведені шляхом вимірювання часу їх польоту через лінію променя довжини\(l = 8.4\: m\). Електричні імпульси реєструвалися на осцилографі на початку і кінці часу польоту\(t\). Енергії були підтверджені калориметрією. \(\PageIndex{3}\)На малюнку показаний зразок фотографії сліду осцилографа в\(V = 1.5\: MeV\).

Малюнок\(\PageIndex{3}\): Кожне горизонтальне поділ становить 9,8 нс.

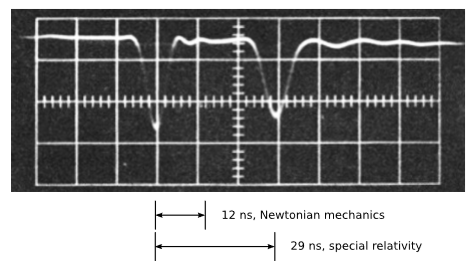
Передбачення ньютонівської фізики виглядає наступним чином.

\[eV = \frac{1}{2}mv^2\]

\[\frac{v}{c} = 2.4\]

\[t = 12\: ns\]

Відповідно до особливої відносності, ми маємо:

\[eV = m(\gamma -1)c^2\]

\[\frac{v}{c} = \sqrt{1 - \left ( 1 + \frac{eV}{mc^2} \right )^{-2}} = 0.97\]

\[t = 29\: ns\]

Результати суперечать ньютонівському прогнозу і узгоджуються з особливою відносністю. На думку Ньютона, ця кількість енергії повинно було прискорити електрони до декількох разів швидкості світла. Насправді ми бачимо наочну демонстрацію природи\(c\) як граничної швидкості.

Приклад\(\PageIndex{4}\): Gravity bending light

Малюнок\(\PageIndex{4}\): Гравітація вигину світла.

Гравітація - це універсальне тяжіння між речами, які мають масу, і оскільки енергія в пучку світла еквівалентна деякій дуже невеликій кількості маси, на світло повинна впливати гравітація, хоча ефект повинен бути дуже малим. Перше експериментальне підтвердження відносності прийшло в 1919 році, коли спостерігалося, що зірки поруч із сонцем під час сонячного затемнення трохи змістилися зі свого звичайного положення. (Якби затемнення не було, відблиски сонця заважали б спостерігати за зірками.) Зоряне світло було вражено гравітацією сонця. Фігура\(\PageIndex{4}\) є фотографічним негативом, тому коло, яке здається яскравим, насправді є темним обличчям Місяця, а темна область - це справді яскрава корона сонця. Зірки, позначені лініями вище і нижче тоді, з'являлися на позиціях, трохи інших, ніж їх звичайні.

Майте на увазі, що ці аргументи дуже грубі та якісні, і неможливо створити релятивістську теорію гравітації, просто взявши\(E = mc^2\) та поєднавши її із законом гравітації Ньютона. Адже цей закон взагалі не стосується часу: він передбачає, що гравітаційні сили поширюються миттєво. Ми знаємо, що це не може бути узгоджено з відносністю, яка забороняє причиною та наслідкам поширюватися з будь-якою швидкістю, більшою ніж\(c\). Щоб створити релятивістську теорію гравітації, нам потрібна загальна теорія відносності.

Подібні міркування говорять про те, що можуть бути зірки - чорні діри - настільки щільні, що їх гравітація може перешкодити виходу світла. Такі зірки були виявлені, і їх властивості, здається, поки що правильно описані загальною відносністю.