1.3: Вимірювання
- Page ID
- 77330
Цілі навчання
- Вимірювання відносності
Ми хотіли б мати загальну систему вимірювання відносності, але поки що у нас є лише неповний печворк. Довжину часового вектора можна визначити як час, виміряний на годиннику, який рухається вздовж вектора. Вектор, подібний до пробілу, має довжину, яка вимірюється на лінійці, рух якої такий, що в рамці відліку лінійки кінцеві точки вектора є одночасними. Але не існує третього вимірювального приладу, призначеного для вимірювання світлоподібних векторів.
Також ми автоматично отримуємо повну систему вимірювання, лише визначивши координати Мінковського. Наприклад, ми ще не знаємо, як знайти довжину часового вектора, такого як\((\Delta t,\Delta x) = (2,1)\), і ми підозрюємо, що вона не буде рівною\(2\), оскільки експеримент Хафела-Кітінга говорить нам, що годинник, який переживає рух, представлений\(\Delta x = 1\), ймовірно, не погодиться з годинником, що переноситься спостерігач, годинник якого ми використовували при визначенні цих координат.
Інваріанти
Вся тема вимірювання схильна бути заплутаною, тому що мінливий ландшафт відносності змушує нас відчувати себе так, ніби ми увійшли в пейзаж Сальвадора Далі, що тануть кишенькові годинники. Хороший спосіб повернути наші підшипники - шукати інваріантні величини: вони однакові у всіх системах відліку. Евклідовий інваріант, такий як довжина або кут, - це той, який не змінюється під обертаннями: усі спостерігачі погоджуються про його значення, незалежно від орієнтацій їхніх систем відліку. Для релятивістського інваріанту ми вимагаємо крім того, щоб спостерігачі погоджувалися незалежно від того, який стан руху вони мають. (Перетворення, яке змінюється від однієї інерційної системи відліку до іншої, без будь-якого обертання, називається імпульсом.)
Електричний заряд - хороший приклад інваріанта. Електрони в атомах зазвичай мають швидкості\(0.01\) до\(0.1\) (в наших релятивістських одиницях, де \(c = 1\)), тому якщо заряд електрона залежав від його руху відносно спостерігача, атоми не були б електрично нейтральними. Експерименти були зроблені, щоб перевірити це до феноменальної точності однієї частини в\(10^{21}\), з нульовими результатами.
Вектор ніколи не може бути інваріантним, оскільки він змінює напрямок при обертанні. (Деякі вектори, такі як швидкості, також змінюються під імпульсом.) У механіці першокурсників будь-яка кількість, наприклад енергія, яка не була вектором, зазвичай потрапляла в категорію, яку ми називали скалярами. Однак у відносності термін «скалярний» має набагато більш обмежувальне визначення, про яке ми поговоримо в розділі 6.2.
До речі, новачки в теорії відносності іноді плутаються з приводу інваріантності на відміну від збереження. Вони не одне і те ж, і ні інше не означає. Наприклад, імпульс має напрямок у просторі, тому він явно не є інваріантним - але ми побачимо в розділі 4.3, що існує релятивістська версія вектора імпульсу, яка зберігається. Як і в ньютонівській механіці, нам байдуже, чи всі спостерігачі погоджуються з імпульсом системи - ми дбаємо лише про те, щоб закон збереження імпульсу був дійсним і мав однакову форму у всіх рамках. І навпаки, є кількості, які є інваріантними, але не збереженими, прикладом є маса.
Метрика
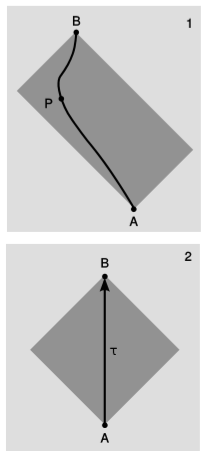
Площа в\(1+1\) розмірах також є інваріантною, як доведено в розділі 2.5. Інваріантність площі має мало значення сама по собі, але вона забезпечує хороший крок до релятивістської системи вимірювання. Припустимо, що у нас відбуваються події\(A\) (Карл VII відновлений на престолі) і\(B\) (Жанна д'Арк страчена). Тепер уявіть, що технологічно просунуті інопланетяни хочуть бути присутніми на обох\(A\) і\(B\), але в проміжок часу вони бажають полетіти на своєму космічному кораблі, бути присутніми на якомусь іншому заході\(P\) (можливо, прес-конференції, на якій вони дають оновлену інформацію про події, що відбуваються на землі), але поверніться назад вчасно для\(B\). Оскільки ніщо не може йти швидше\(c\) (що ми приймаємо рівним\(1\)),\(P\) не може бути занадто далеко. Безліч всіх можливих подій\(P\) утворює прямокутник, фігуру\(\PageIndex{1}\), в\(1+1\) -мірній площині, який має\(A\) і\(B\) на протилежних кутах і краї якого мають ухили рівні\(\pm 1\). Цей тип прямокутника ми називаємо світло-прямокутником.
Площа цього прямокутника буде однаковою незалежно від системи відліку. Зокрема, ми могли б вибрати спеціальну систему відліку, панель\(2\) малюнка, таку, що\(A\) і\(B\) відбуваються в одному і тому ж місці. (Вони не зустрічаються в одному і тому ж місці, наприклад, в рамі сонця, тому що земля крутиться і обходить сонце.) Так як швидкість \(c = 1\)однакова у всіх рамках відліку, а сторони прямокутника мали укоси\(\pm 1\) в рамі\(1\), вони все одно повинні мати ухили\(\pm 1\) в рамі\(2\). Прямокутник стає квадратом, діагоналі якого є рамкою\(o\) і\(s\) для\(2\). Довжина цих діагоналей дорівнює часу, що\(\tau\) минув на годиннику, який знаходиться в стані спокою в кадрі\(2\), тобто годиннику, який ковзає по простору з постійною швидкістю від\(A\) до\(B\), возз'єднавшись з планетою Земля, коли її орбіта приводить її до\(B\). Площа сірих областей можна інтерпретувати як половину квадрата цього ковзаючого годинникового часу, яке називається належним часом. «Правильне» тут використовується в дещо архаїчному сенсі «власний» або «себе», як у «Ватикан не лежить в межах самої Італії. » Правильний час, який ми відзначаємо\(\tau\), можна визначити лише для часових світових ліній, оскільки світлоподібна або космічна світова лінія неможлива для матеріального годинника.
З точки зору координат (Мінковського), припустимо, що події\(A\) і\(B\) розділені на відстань\(x\) і час\(t\). Тоді взагалі\(t^2 - x^2\) дає квадрат ковзання-годинника часу.
Доказ: Через те, як площа масштабується з масштабуванням координат, вираз повинен мати форму\((...)t^2+(...)tx+(...)x^2\), де кожен\((...)\) представляє безодиничну константу. \(tx\)Коефіцієнт повинен дорівнювати нулю за ізотропією простору. \(t^2\)Коефіцієнт повинен дорівнювати для\(1\) того, щоб дати правильну відповідь в разі\(x = 0\), де координатами є координати спостерігача в спокої щодо годинника. Так як площа зникає для\(x = t\),\(x^2\) коефіцієнт повинен дорівнювати\(-1\). Коли\(|x|\) більше\(|t|\), події\(A\) і\(B\) знаходяться настільки далеко один від одного в просторі і настільки близько один до одного в часі, що неможливо було б мати причинно-наслідковий зв'язок між ними, оскільки\(c = 1\) це максимальна швидкість причини та наслідків. У цій ситуації\(t^2 - x^2\) негативний і не може бути інтерпретований як годинник часу, але його можна інтерпретувати як мінус квадрат відстані між\(A\) і\(B\), як вимірюється в системі відліку, в якій\(A\) і\(B\) є одночасними.
Узагальнюючи до\(3+1\) розмірів і до будь-якого вектора\(v\), а не просто зміщення в просторові/часі, ми маємо вимір вектора, визначеного
\[ v^{2}_{t} - v^{2}_{x} - v^{2}_{y} - v^{2}_{z} \]
В особливому випадку, коли \(v\)є зміщенням просторучасу, це можна назвати просторово-часовим інтервалом. За винятком знаків, це дуже схоже на теорему Піфагора, яка є окремим випадком векторного крапкового добутку. Тому ми визначаємо функцію, яка\(g\) називається метрикою.
\[ g( \textbf {u}, \textbf {v}) = u_{t}v_{t} - u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z} \]
Через аналогію з евклідовим точковим добутком ми часто використовуємо позначення\(u\cdot v\) для цієї величини, і іноді називаємо його внутрішнім твором. Метрика є центральним об'єктом відносності. Взагалі відносність, яка описує гравітацію як кривизну просторучасу, коефіцієнти, що виникають на правій стороні\(\pm 1\), більше не є, але повинні змінюватися від точки до точки. Навіть у спеціальній теорії відносності, де коефіцієнти можна зробити постійними, визначення\(g\) довільне аж до ненульової мультиплікативної константи, і зокрема багато авторів визначають\(g\) як негативне нашого визначення. Знакова конвенція, яку ми використовуємо, є найпоширенішою у фізиці частинок, тоді як протилежне частіше зустрічається у класичній теорії відносності. Набір знаків,\(+---\) або\(-+ ++\), називається підписом метрики. У розділі 1.1 ми розробили ідею ортогональності просторово-часових векторів з фізичною інтерпретацією, що якщо спостерігач рухається вздовж вектора\(o\), вектор s, ортогональний до,\(o\) є вектором одночасності. Це відповідає зникненню внутрішнього добутку\(o\cdot s = 0\), і лише недосконало аналогічно ідеї про те, що евклідові вектори перпендикулярні, якщо їх крапковий добуток дорівнює нулю. Зокрема, ненульовий евклідовий вектор ніколи не перпендикулярний самому собі, але для будь-якого світлоподібного вектора\(v\) ми маємо\(v\cdot v = 0\). Метрика не дає нам міри довжини світлоподібних векторів. Фізично ні лінійка, ні годинник не можуть виміряти такий вектор.
Метрика в одиницях СІ
Одиниці з\(c = 1\) відомі як природні одиниці. (Вони є природними для відносності в тому ж сенсі, що одиниці з\(\tilde{h} = 1\) є природними для квантової механіки.) Будь-яке рівняння, виражене в натуральних одиницях, може бути перевиражено в одиницях СІ простим доцільним вставляти коефіцієнти,\(c\) де вони потрібні, щоб отримати одиниці, які мають сенс. Результат для метрики може бути
\[g( \textbf{u}, \textbf{v}) = c^{2}u_{t}v_{t} - u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z}\]
або
\[g(\textbf{u},\textbf{v}) = u_{t}v_{t} - (u_{x}v_{x} - u_{y}v_{y} - u_{z}v_{z})/c^{2}\]
Не має значення, який ми вибираємо, оскільки метрика довільна до постійного коефіцієнта. Перший вираз дає результат в метрах, друге - секунди.
Ортогональні світлові промені?
На просторово-часовій діаграмі в\(1+1\) розмірах зображуємо світловий конус з двома лініями\(x = \pm t\), намальованими під кутом\(90\) градусів відносно один одного. Чи є ці лінії ортогональними? .
Ні. Наприклад, якщо\(u = (1,1)\) і\(v = (1,-1)\), то\(u\cdot v\) є\(2\), не нуль.
Піонер 10
Космічний зонд Pioneer 10 був запущений в 1972 році, а в 1973 році був першим кораблем, який пролетів планетою Юпітер. Вона перетнула орбіту планети Нептун в 1983 році, після чого телеметричні дані отримували аж до 2002 року. Наступна таблиця дає положення космічного корабля щодо Сонця рівно опівночі 1 січня 1983 року та 1 січня 1995 року. Дата 1983 приймається бути\(t = 0\).
| т (и) | х | у | z |
| 0 | 1 784 × 10 12 м | 3 951 × 10 12 м | 0,237 × 10 12 м |
| 3,7869 × 10 8 с | 2,420 × 10 12 м | 8,827 × 10 12 м | 0,488 × 10 12 м |
Порівняйте час, що минув на космічному кораблі, з часом в рамках відліку, прив'язаного до сонця.
Ми можемо перетворити ці дані в природні одиниці, причому одиниця відстані є другою (тобто світловою секундою, відстань світла проходить за одну секунду), а одиниця часу - секунди. Конвертуючи і здійснюючи це віднімання, ми маємо:
| \( \Delta t \) | \( \Delta x \) | \( \Delta y \) | \( \Delta z \) |
| 3,786912 × 10 8 с | 0,2121 × 10 4 с | 1,626 × 10 4 с | 0,084 × 10 4 с |
Порівнюючи показники часових і просторових чисел, ми можемо побачити, що космічний апарат рухався зі швидкістю на порядку швидкості світла, тому релятивістські ефекти повинні бути невеликими, але не зовсім незначними.\(10^{-4}\) Оскільки інтервал схожий на час, ми можемо взяти його квадратний корінь і інтерпретувати його як час, що минув на космічному кораблі. Результат є\(\tau = 3.786911996×108\, s\). Це\(0.4\, s\) менше часу, що минув у системі відліку сонця.
Гамма-фактор
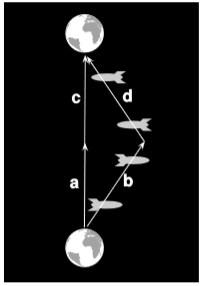
\(\PageIndex{2}\)Малюнок - релятивістська версія прикладу 1.1.1. Ми маємо намір проаналізувати його за допомогою метрики, і оскільки метрика дає однаковий результат у будь-якому кадрі, ми вибрали для зручності представлення її в кадрі, в якому земля знаходиться в стані спокою. У нас\(v\) є\(a = (t,0)\) і\(b = (t,vx)\), де швидкість космічного корабля щодо землі. Застосування метрики дає належний час\(t\) для земляного близнюка і\(t \sqrt{1-v^{2}}\) для подорожуючого близнюка. Ті ж результати застосовуються для\(c\) і\(d\). Результатом є те, що земний близнюк переживає час, який більший за коефіцієнтом\(\gamma\) (грецька буква гамма), визначений як\(\gamma = 1/ \sqrt{1-v^{2}}\). Якщо\(v\) поруч\(c\),\(\gamma\) може бути великим, і ми виявляємо, що коли астронавт-близнюк повертається додому, ще молодий, земний близнюк може бути старим і сірим. Свого часу це називалося парадоксом близнюків, і це вважалося парадоксальним або тому, що це, здавалося, кидає виклик здоровому глузду, або тому, що подорожуючий близнюк міг стверджувати, що вона була в спокої, поки земля рухалася. Порушення здорового глузду - це насправді те, що спостерігалося в експерименті Хафела-Кітінга, і останній аргумент є помилковим з тих же причин, що і в галілейській версії, наведеній у прикладі 1.1.1.
У нас в цілому таке тлумачення:
Час розширення
Годинник працює найшвидше в рамках відліку спостерігача, який знаходиться в стані спокою щодо годинника. Спостерігач в русі щодо тактової частоти\(v\) сприймає годинник як біжать повільніше в рази\(\gamma\).
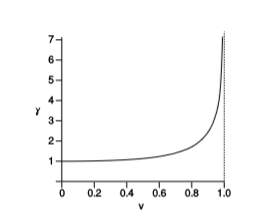
Хоча це формулюється з точки зору годинників, ми інтерпретуємо це як те, що говорить нам щось про сам час. Ставлення полягає в тому, що ми повинні визначити поняття з точки зору операцій, необхідних для його вимірювання: час визначається як те, що вимірює годинник. Ця філософія, яка була надзвичайно впливовою серед фізиків, називається операціоналізмом і була розроблена П.У.Бріджманом в 1920-х роках Наше оперативне визначення часу працює, оскільки на швидкість всіх фізичних процесів однаково впливає розширення часу. На той час, коли близнюки в фігурі\(\PageIndex{2}\) возз'єдналися, подорожуючий близнюк не тільки чув менше кліщів від її антикварних механічних кишенькових годинників, але вона також мала менше серцевих скорочень, і атомний годинник корабля погоджується з її годинником в межах точності годинника.
Затримка часу симетрична в тому сенсі, що вона розглядає всі рамки відліку демократично. Якщо спостерігачі\(A\) і\(B\) не перебувають у спокої відносно один одного, то\(A\) каже, що\(B’s\) час працює повільно, але\(B\) каже,\(A\) що це повільний. На малюнку\(\PageIndex{2}\) закони фізики не роблять різниці між рамками відліку, які збігаються з векторами\(a\) і\(b\); як і у відповідному Галілеєвському випадку прикладу 1.1.1, асиметрія виникає тому, що\(a\) і\(c\) паралельні, але \(b\)і не\(d\) є.
Як показано в прикладі\(\PageIndex{4}\) нижче, послідовність вимагає, щоб крім впливу на час ми мали подібний вплив на відстані:
скорочення довжини
Метр-палиця здається найдовшою спостерігачеві, який перебуває у спокої щодо неї. Спостерігач рухається відносно метра-палиці в\(v\) observes the stick to be shortened by a factor of \(\gamma\).
Візуалізація стиснення довжини в плані просторово-часових діаграм представлена на малюнку 1.4.3. Наше сьогоднішнє обговорення обмежується\(1+1\) розмірами\(3+1\), але в, тільки довжина уздовж лінії руху скорочується.
Міжзоряна дорожня подорож
Аліса залишається на землі, поки її близнюк Бетті вирушає на космічному кораблі для Тау Кеті, сусідньої зірки. Тау Цеті-це\(12\) light-years away, so even though Betty travels at \(87\%\) of the speed of light, it will take her a long time to get there: \(14\) years, according to Alice.

Бетті відчуває розширення часу. На такій швидкості вона\(\gamma\) є\(2.0\), так що плавання буде здаватися їй лише минулими\(7\) роками. Але існує ідеальна симетрія між рамками відліку Аліси та Бетті, тому Бетті погоджується з Алісою щодо їх відносної швидкості. Бетті бачить себе в стані спокою, тоді як сонце і Тау Кеті обидва рухаються назад зі швидкістю світла.\(87\%\) Як же тоді вона може спостерігати Тау Кеті, щоб дістатися до неї лише за\(7\)\(14\) роки, коли на таку швидкість повинні пройти\(12\) роки?
Потрібно враховувати скорочення довжини. Бетті бачить, що відстань між сонцем і Тау Ceti скорочується в рази\(2\). Те ж саме відбувається з Алісою, яка спостерігає за Бетті та її космічним кораблем, щоб бути передбаченими.
Рухомий атомний годинник
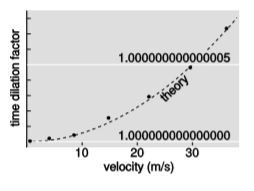
Розширюючись\(\gamma\) у серії Тейлора\(\gamma \approx 1 - v^{2}/2\), so that when \(v\) is small, relativistic effects are approximately proportional to \(v^2\), ми знаходимо, тому дуже важко спостерігати їх на низьких швидкостях. Це стало причиною того, що експеримент Хафель-Кітінга був проведений на борту пасажирських літаків, які літають на високих швидкостях. Струмені, однак, літають на великій висоті, і це приносить в другий раз ефект розширення, загально-відносний вістичний один через гравітацію. Основна мета експерименту полягала в тому, щоб перевірити цей ефект. Лише через чотири десятиліття після Хафеле та Кітінга хтось зробив концептуально простий експеримент з атомним годинником, в якому єдиним ефектом був рух, а не гравітація. Однак у 2010 році Chou et al.7 вдалося побудувати атомний годинник, достатньо точний, щоб виявити розширення часу на швидкості настільки низькою, як\(10\, m/s\). Figure \(\PageIndex{5}\) показує їх результати. Оскільки рухати весь годинник було непрактично, експериментатори лише перемістили атоми алюмінію всередині годинника, що насправді змусило його «галочкою».
Велика тимчасова дилатація
Ефекти розширення часу, описані в прикладі,\(\PageIndex{5}\) були дуже невеликими. Якщо ми хочемо побачити великий ефект розширення часу, ми не можемо зробити це з чимось розміром атомних годин, які вони використовували; кінетична енергія була б більшою, ніж загальний мегатоннаж усіх світових ядерних арсеналів. Однак ми можемо прискорити субатомні частинки до швидкості, з якою\(\gamma\) велика. Для експериментальних фізиків частинок відносність - це те, що ви робите цілий день, перш ніж відправитися додому і зупинитися в магазині за молоком. Ранній, низькоточний експеримент такого роду був проведений Россі і Холлом в 1941 році, використовуючи природні космічні промені. \(\PageIndex{6}\)На малюнку показаний експеримент 1974 подібного типу, який перевіряв розширення часу, передбачене відносністю, з точністю близько однієї частини на тисячу.

Частинки\(\mu\), звані мюонами (названі на честь грецької літери «myoo»), вироблялися прискорювачем в ЦЕРН, недалеко від Женеви. Мюон - це, по суті, важча версія електрона. Мюони піддаються радіоактивному розпаду, триваючи в середньому лише\(2.197\, µs\) before they evaporate into an electron and two neutrinos. The 1974 experiment was actually built in order to measure the magnetic properties of мюони, але він виробляв високоточний тест розширення часу як побічний продукт. Оскільки мюони мають такий же електричний заряд, як електрони, їх можна захопити за допомогою магнітних полів. Мюони вводили в кільце, показане на малюнку \(\PageIndex{6}\), кружляли навколо нього, поки вони не зазнали радіоактивного розпаду. На швидкості, з якою рухалися ці мюони, у них було\(\gamma = 29.33\), тому в середньому вони тривали\(29.33\) times longer than the normal lifetime. In other words, they were like tiny alarm clocks that самознищуватися в випадково обраний час. Графік показує кількість підрахованих радіоактивних розпадів, як функція часу, що минув після того, як даний потік мюонів був введений в кільце для зберігання. Дві пунктирні лінії показують швидкості розпаду, передбачені з відносністю та без неї. Релятивістська лінія - це та, яка погоджується з експериментом.
