4.6: Закони про збереження
- Page ID
- 77577
Немає загальних законів про збереження
Деякі з перших тензорів, про які ми обговорювали, були маса і заряд, як тензори рангу 0, так і тензор імпульсу рангу 1, який містить як класичну енергію, так і класичний імпульс. Фізики спочатку вирішили, що маса, заряд, енергія та імпульс цікаві, оскільки ці речі були збережені. Це робить природним запитати, як закони збереження можуть бути сформульовані в теорії відносності. Ми звикли висловлювати закони збереження випадково з точки зору кількості чогось у всьому Всесвіті, наприклад, що класично загальна кількість маси у Всесвіті залишається постійною. Відносність дозволяє нам робити фізичні моделі Всесвіту в цілому, тому здається, що ми повинні бути в змозі говорити про закони збереження в теорії відносності.
- Ми не можемо.
По-перше, як ми визначаємо «залишається постійним?» Одночасність не є чітко визначеною, тому ми не можемо просто зробити два знімки, назвати їх початковим і кінцевим, і порівняти загальну кількість, скажімо, електричного заряду в кожному знімку. Ця складність не є непереборною. Як на малюнку а, ми можемо довільно вибирати тривимірні космічні поверхні - одну початкову та одну кінцеву - і інтегрувати заряд над кожною. Закон збереження заряду говорить про те, що незалежно від того, яку космічну поверхню ми вибрали, загальний заряд на кожному буде однаковим.

Далі є питання, що інтеграл може розходитися, особливо якщо Всесвіт був просторово нескінченним. А поки давайте припустимо просторово скінченний Всесвіт. Для простоти припустимо, що вона має топологію три-сфери (див. Розділ 8.2 для запевнення, що це не фізично необгрунтовано), і ми можемо візуалізувати її як двосферу.

У випадку імпульсу чотири вектора, в якій системі координат ми б висловили це? Загалом, ми навіть не очікуємо, що зможемо визначити гладку, добре поведену систему координат, яка охоплює весь Всесвіт, і навіть якби ми це зробили, не було б сенсу додавати вектор, виражений у цій системі координат в точці А, до іншого вектора з точки B; найкраще, що ми могли б зробити, було б паралельно- перенесіть вектори в одну точку, а потім додайте їх, але паралельний транспорт залежить від шляху. (Подібні проблеми виникають з моментом імпульсу.) З цієї причини давайте обмежимося більш легким випадком скаляра, такого як електричний заряд.
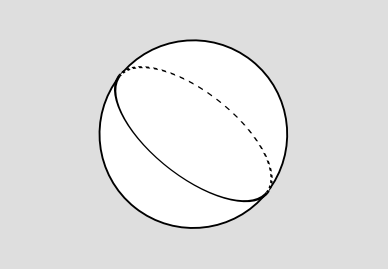
Але зараз у нас справжня біда. Як би ми насправді вимірювали загальний електричний заряд Всесвіту? Єдиний спосіб зробити це - виміряти електричні поля, а потім застосувати закон Гаусса. Це вимагає від нас виділити якусь поверхню, на яку ми можемо інтегрувати потік, як на малюнку 4.5.2. Це дійсно двовимірна поверхня на трисфері, але ми можемо візуалізувати її як одновимірну поверхню — замкнуту криву — на двосфері. Але тепер припустимо, що ця крива являє собою велике коло, малюнок 4.5.3. Якщо ми виміряємо загальний потік, що не зникає через нього, як ми знаємо, де знаходиться заряд? Це може бути з будь-якого боку.
Висновок полягає в тому, що закони збереження мають сенс у відносності лише за особливих обставин. 16 У нас немає нічого подібного до наддугових, глобальних принципів збереження. Як приклад відповідних особливих обставин, розділ 6.2 показує, як визначити збережені величини, які поводяться як енергія та імпульс, для руху тестової частинки в певній метриці, яка має певну симетрію. Це узагальнено в розділі 7.1 до загального, глобального закону збереження, що відповідає кожній безперервній симетрії простору-часу.
Примітка
Ще один аргумент, що призводить до такого ж висновку, див. Розділ 7.5.
Збереження кутового моменту та перетягування кадру
Інший особливий випадок, коли закони збереження працюють, полягає в тому, що якщо простір, який ми вивчаємо, стає дуже плоским на великих відстанях від невеликої системи, яку ми вивчаємо, то ми можемо визначити далеку межу, яка оточує систему, виміряти потік через цю межу та знайти заряд системи. Для такого асимптотичного простору площинності ми також можемо обійти проблеми, які виникають із збереженими векторами, такими як імпульс. (Асимптотична площинність більш детально розглядається в розділі 7.4.) Якщо просторово-час далеко майже плоский, то паралельний транспорт втрачає свою залежність від шляху, тому ми можемо однозначно визначити поняття паралельного транспортування всіх внесків до потоку в одну довільно обрану точку P, а потім додати їх. Асимптотична площинність також дозволяє визначити приблизне поняття глобального кадру Лоренца, так що вибір P не має значення.
Як приклад, на малюнку 4.5.4 показаний струмінь речовини, що викидається з галактики M87 на ультрарелятивістських порах. Синій колір струменя на зображенні видимого світла походить від синхротронного випромінювання, яке представляє собою електромагнітне випромінювання, що випромінюється релятивістськими зарядженими частинками, прискореними магнітним полем. Вважається, що струмінь надмасивної чорної діри в центрі М87. Випромінювання струменя в певному напрямку говорить про те, що чорна діра не сферично симетрична. Здається, з ним пов'язана певна вісь. Як це може бути? Сферична симетрія нашого сонця порушена існуванням зовнішніх спостережуваних ознак, таких як сонячні плями та екваторіальна опуклість, але єдина інформація, яку ми можемо отримати про чорну діру, походить від її зовнішніх гравітаційних (і, можливо, електромагнітних) полів. Здається, що щось про метрику простору-часу, що оточує цю чорну діру, порушує сферичну симетрію, але зберігає симетрію щодо якоїсь бажаної осі. Який аспект початкових умов при утворенні отвору могла б визначити таку вісь? Найбільш вірогідним кандидатом є момент моменту. Таким чином, ми змушені підозрювати, що чорні діри можуть мати кутовий імпульс, що кутовий момент зберігає інформацію про їх утворення, і що кутовий імпульс зовні виявляється через його вплив на метрику простору-часу.

Якою була б форма такої метрики? Сферичні координати в плоскому просторовомучасі дають метрику, подібну до цього:
\[ds^{2} = dt^{2} - dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]
Ми побачимо в розділі 6, що для чорної діри, що не обертається, метрика має вигляд
\[ds^{2} = (\ldots) dt^{2} - (\ldots) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]
де (.) представляє функції r Насправді немає нічого особливого в метриці чорної діри, принаймні далеко; та ж зовнішня метрика застосовується до будь-якого сферично симетричного, що не обертається тіла, типу Місяця. А як щодо метрики тіла, що обертається? Ми очікуємо, що він матиме такі властивості:
- Він має умови, які є непарними під час розвороту, що відповідає розвороту кутового імпульсу тіла.
- Аналогічно він має члени, які є непарними при розвороті диференціала d\(\phi\) азимутальної координати.
- Метрика повинна мати осьову симетрію, тобто вона повинна бути незалежною від\(\phi\).
Обмежуючи нашу увагу на екваторіальній площині\(\theta = \frac{\pi}{2}\), найпростіша модифікація, яка має ці три властивості, - додати термін форми
\[f(\ldots) L d \phi dt,\]
де (..) знову дає r-залежність і L - константа, інтерпретується як кутовий момент. Детальна обробка виходить за рамки цієї книги, але рішення цієї форми релятивістських польових рівнянь були знайдені новозеландським фізиком Роєм Керром в 1963 році в Техаському університеті в Остіні.
Астрофізичне моделювання спостережень, таких як фігура d, є складним, але ми можемо побачити в спрощеному експерименті думки, що якщо ми хочемо визначити кутовий імпульс тіла, що обертається через його гравітаційне поле, це буде важко, якщо ми не використаємо процес вимірювання, який використовує переваги асимптотичного рівність простору. Наприклад, припустимо, що ми посилаємо два пучка світла повз землю, в її екваторіальній площині, по одному з кожного боку, і вимірюємо їх прогини, тобто прогини будуть різними, тому що знак d\(\phi\) dt буде протилежним для двох пучків. Але все поняття «відхилення» має сенс лише в тому випадку, якщо у нас є асимптотично плоский фон, на що вказують пунктирні дотичні лінії. Крім того, якщо просторовий час не був асимптотично плоским в цьому прикладі, то не може бути однозначного способу визначити, чи була асиметрія обумовлена обертанням землі, якимось зовнішнім фактором або якимось взаємодією між землею та іншими тілами поблизу.

Виходить і так, що гіроскоп в такому гравітаційному полі прецесує. Цей ефект, який називається перетягуванням кадру, був передбачений Lense і Thirring в 1918 році, і був остаточно перевірений експериментально в 2008 році шляхом аналізу даних експерименту Gravity Probe B з точністю близько 15%. Експеримент був влаштований таким чином, що відносно сильний геодезичний ефект (6,6 дугових секунд на рік) та набагато слабший ефект об'єктива Thirring (.041 arc-sec/yr) створювали прецесії в перпендикулярних напрямках. Знову ж таки, була задіяна наявність асимптотично плоского фону, оскільки зонд вимірював орієнтації своїх гіроскопів щодо направляючої зірки ІМ. М.

