2.3: Парабола

Ми визначаємо параболу як локус точки, яка рухається таким чином, що її відстань від фіксованої прямої лінії, яка називається директрисою, дорівнює її відстані від нерухомої точки, яка називається фокусом s. На відміну від еліпса, парабола має лише один фокус і одну директрису. Однак порівняння цього визначення з властивістю focus - directrix еліпса (яке також може бути використано для визначення еліпса) показує, що параболу можна розглядати як граничну форму еліпса з ексцентриситетом, рівним одиниці.

Ми знайдемо рівняння до параболи, директриса якої є лінією,$y = −q$ а фокус якої - точка$(q , 0)$. $\text{II.20}$На малюнку показана парабола. $\text{F}$є фокусом і$\text{O}$ є початком системи координат. Вершина параболи знаходиться біля початку. В орбітальному контексті, наприклад, орбіта комети, що рухається навколо Сонця на параболічній орбіті, Сонце буде у фокусі$\text{F}$, а відстань між вершиною та фокусом буде перигелійну відстань, для якої символ традиційно$q$ використовується в теорії орбіти.

$\text{FIGURE II.20}$

З малюнка видно$\text{II.20}$, що визначення параболи$(\text{PF} = \text{PN})$ вимагає, щоб

$$(x-q)^2 + y^2 = (x+q)^2 , \label{2.4.1}$$

з якого

$$y^2 = 4qx , \label{2.4.2}$$

що є рівнянням до параболи.

Вправа$\PageIndex{1}$

Намалюйте наступні параболи:

1. $y^2 = -4qx$
2. $x^2 = 4qy$
3. $x^2 = -4qy,$
4. $(y-2)^2 = 4q (x-3).$

Лінія, паралельна$y$ -осі і проходить через вогнище - це латус пряма кишка. Заміна$x = q$ в$y^2 = 4ax$ показує, що латус прямої кишки перетинає параболу в двох точках$(q , \pm 2q)$, і що довжина$l$ напівширокої прямої кишки є$2q$.

Рівняння

$$x = qt^2 , \quad y = 2qt \label{2.4.3}$$

є параметричними рівняннями до параболи, для$y^2 = 4qx$ результатів ліквідації$t$ між ними. Іншими словами, якщо$t$ будь-яка змінна, то будь-яка точка, яка задовольняє цим двом рівнянням, лежить на параболі.

Більшість читачів буде знати, що якщо частинка рухається з постійною швидкістю в одному напрямку і постійним прискоренням під прямим кутом до цього напрямку, як у кулі, що проектується в рівномірному гравітаційному полі або електроном, що рухається в рівномірному електричному полі, шлях є параболою. У напрямку постійної швидкості відстань пропорційна часу, а в постійному напрямку прискорення відстань пропорційна квадрату часу, а отже, шлях є параболою.

Дотичні до параболи.

Де пряма$y = mx + c$ перетинає параболу$y^2 = 4qx$? Відповідь можна знайти шляхом підміни$mx + c$ для$y$ отримання, після перестановки,

$$m^2 x^2 + 2(mc - 2q) x + c^2 = 0 . \label{2.4.4}$$

Лінія є дотичною, якщо дискримінант дорівнює нулю, що призводить до

$$c = q/m . \label{2.4.5}$$

Таким чином, пряма лінія форми

$$y = mx + q/m \label{2.4.6}$$

дотична до параболи. Малюнок$\text{II.22}$ ілюструє це для декількох ліній, нахили кожної відрізняються$5^\circ$ від наступної.

$\text{FIGURE II.22}$

Тепер ми виведемо рівняння до лінії, яка є дотичною до параболи в точці$(x_1 , y_1 )$.

$(x_1 , y_1) = (qt_1^2 , 2qt_1)$Дозволяти точка на параболі, і
$(x_2 , y_2) = (qt_2^2 , 2qt_2)$ Дозволяти бути ще однією точкою на параболі.

Лінія, що з'єднує ці дві точки

$$\frac{y-2qt_1}{x-qt_1^2} = \frac{2q(t_2 - t_1)}{q(t_2^2 - t_1^2)} = \frac{2}{t_2+t_1}. \label{2.4.7}$$

Тепер давайте$t_2$ наблизитися$t_1$, врешті-решт збігаючись з ним. $t_1 = t_2 = t$Введення останніх результатів рівняння, після спрощення, в

$$ty = x + qt^2 , \label{2.4.8}$$

будучи рівняння до дотичної в$(qt^2 , 2qt )$.

Помножте на$2q$:

$$2qty = 2q (x+qt^2) \label{2.4.9}$$

і видно, що рівняння до дотичної$(x_1 , y_1 )$ в

$$y_1 y = 2q (x_1 + x). \label{2.4.10}$$

Існує ряд цікавих геометричних властивостей, деякі з яких наведені тут. Наприклад, якщо дотична до параболи в точці$P$ відповідає директрисі в$Q$, то, так само, як і для еліпса,$P$ і$Q$ субтенд під прямим кутом у фокусі (малюнок$\text{II.23}$). Доказ схожий на те, що дано для еліпса, і залишається для читача.

$\text{FIGURE II.23}$

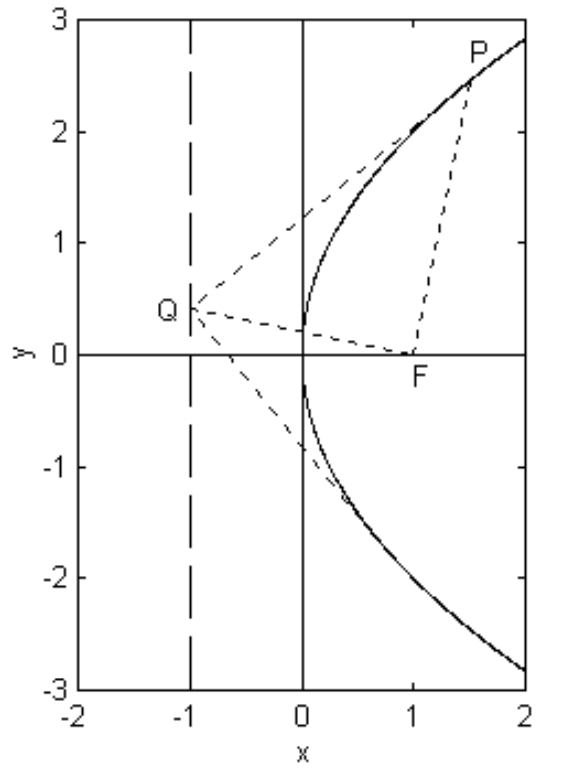
Читач нагадає, що перпендикулярні дотичні до еліпса зустрічаються на директорському колі. Аналогічна теорема проти параболи полягає в тому, що перпендикулярні тангенси зустрічаються на директрисі. Це також проілюстровано на малюнку$\text{II.23}$. Теорема не особливо важлива в теорії орбіт, і доказ також залишається читачеві.

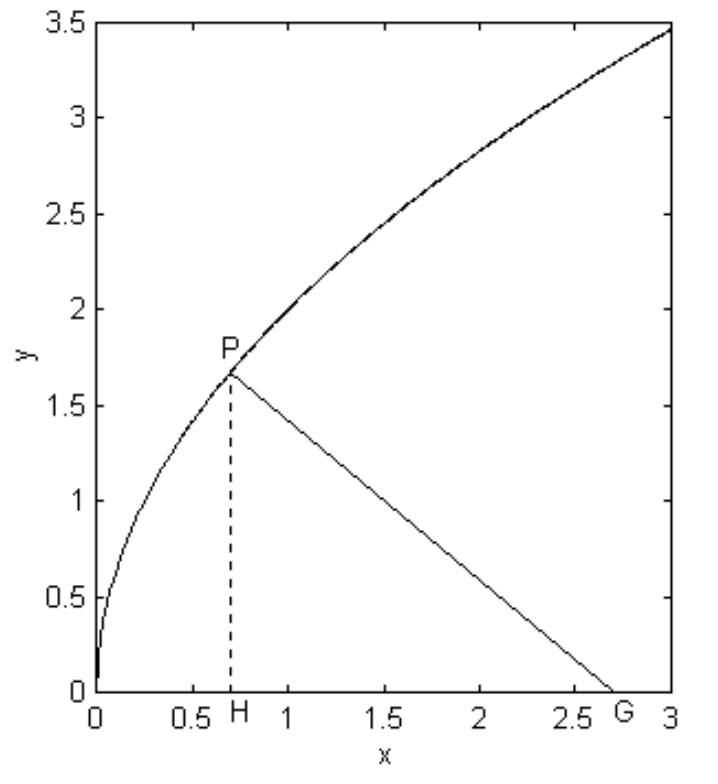
$\text{PG}$Дозволяти бути нормаллю до параболи в точці$\text{P}$, зустрічаючи вісь в$\text{G}$ (рис.$\text{II.24}$). Ми будемо називати довжину$\text{GH}$ субнормальної. Цікавою властивістю є те$l$, що довжина завжди$\text{GH}$ дорівнює довжині прямої кишки semi latus (яка на малюнку$\text{II.24}$ має довжину 2 − тобто ординату де$x = 1$), незалежно від положення$\text{P}$. Цей доказ знову залишається на утриманні читача.

$\text{FIGURE II.24}$

Наступні два геометричні властивості, хоча і не мають негайного застосування до теорії орбіти, безумовно, мають застосування до астрономії.

$\text{FIGURE II.25}$

Тангенс при$\text{P}$ робить кут$\alpha$ з$x$ -віссю, і$\text{PF}$ робить кут$\beta$ з$x$ -віссю (малюнок$\text{II.25}$). Ми покажемо це$\beta = 2\alpha$ і виведемо цікаве наслідок.

Рівняння до дотичної (див. Рівняння$\ref{2.4.8}$) є$ty = x + qt^2$, який показує, що

$$\tan \alpha = 1/t . \label{2.4.11}$$

Координати$\text{P}$ і$\text{F}$ є, відповідно,$\left(qt^2 , 2qt \right)$ і$(q , 0)$, і так, з трикутника$\text{PFH}$, знаходимо.

$$\tan \beta = \frac{2t}{t^2-1}. \label{2.4.12}$$

Нехай$\tau = 1/t$, потім$\tan \alpha = \tau$ і$\tan \beta = 2\tau/(1 - \tau^2)$, який показує, що$\beta = 2\alpha$.

Це також показує,$\text{JFP}$ що трикутник рівнобедрений, з$\text{J}$ кутами під$\text{P}$ кожним істотою$\alpha$. Це також можна показати наступним чином.

З$ty = x + qt^2$ Рівняння ми бачимо, що$\text{J}$ це точка$(−qt^2 , 0)$, так що$\text{JF} = q (t^2 + 1)$.

З$\text{PFH}$ трикутника ми бачимо, що

$$(\text{PF})^2 = 4q^2 t^2 + q^2 \left(t^2 - 1 \right)^2 - q^2 \left( t^2 + 1 \right)^2 . \label{2.4.13}$$

Тому $$\text{PF} = \text{JF} . \label{2.4.14}$$

Так чи інакше, оскільки трикутник$\text{JPF}$ рівнобедрений, то випливає, що$\text{QP}$ і$\text{PF}$ зробити однаковий кут$\alpha$ до дотичної. Якщо парабола є поперечним перерізом телескопічного дзеркала, будь-який промінь світла, що йде паралельно осі, буде зосереджений на$\text{F}$, так що параболоїдальне дзеркало, яке використовується на осі, не страждає від сферичної аберації. (Це властивість тримається, звичайно, тільки для світла, паралельного осі параболоїда, так що параболоїдальне дзеркало без якоїсь корекції дає хороші зображення тільки над вузьким полем зору.)

Тепер розглянемо, що відбувається, коли ви помішуєте чашку чаю. Поверхня набуває форму, яка виглядає так, ніби вона може нагадувати параболу$y = x^2 /(4q)$ - див. Малюнок$\text{II.26}$:

$\text{FIGURE II.26}$

Припустимо, рідина циркулює з кутовою швидкістю$ω$. Чайний лист, що плаває на поверхні, знаходиться в рівновазі (в обертовій опорній рамці) під трьома силами: його вага$mg$, відцентрова сила$mω^2 x$ і нормальна реакція$R$. Нормаль до поверхні робить кут$\theta$ з вертикаллю (а тангенс робить кут$\theta$ з горизонталлю), заданий

$$\tan \theta = \frac{ω^2x}{g}. \label{2.4.15}$$

Але нахил параболи$y = x^2 /(4q)$ такий$x/(2q)$, що поверхня дійсно парабола з підлогою прямої кишки$2q = g/ω^2$.

Це явище було використано в Канаді для створення успішного великого телескопа (діаметра$6 \ \text{m}$), в якому дзеркало являє собою обертається диск ртуті, який приймає ідеально параболоїдальну форму. Іншим прикладом є метод спінового лиття, який успішно використовується для виробництва великих, твердих скляних параболоїдальних дзеркал телескопа. У цьому процесі піч обертається навколо вертикальної осі, в той час як розплавлене скло охолоджується і з часом твердне до необхідного параболоїдного ефекту.

Вправа$\PageIndex{1}$

Дзеркала діаметром 6,5 метрів для подвійних телескопів Магеллана в Лас-Кампаньяс, Чилі, мають фокусне співвідношення$f/1.25$. Вони були зроблені за технікою спинового лиття в Дзеркальній лабораторії Університету Арізони. З якою швидкістю довелося б обертати піч, щоб досягти потрібного фокусного співвідношення? (Відповідь$= 7.4 \ \text{rpm}$.) Зверніть увагу, що$f/1.25$ це досить глибокий параболоїд. Якби це дзеркало було виготовлено традиційним шліфуванням з твердого диска, який обсяг матеріалу довелося б видалити, щоб вийшов потрібний параболоїд? (Відповідь - колосальні 5,4 кубічних метра, або близько 12 тонн!)

Полярне рівняння до параболи

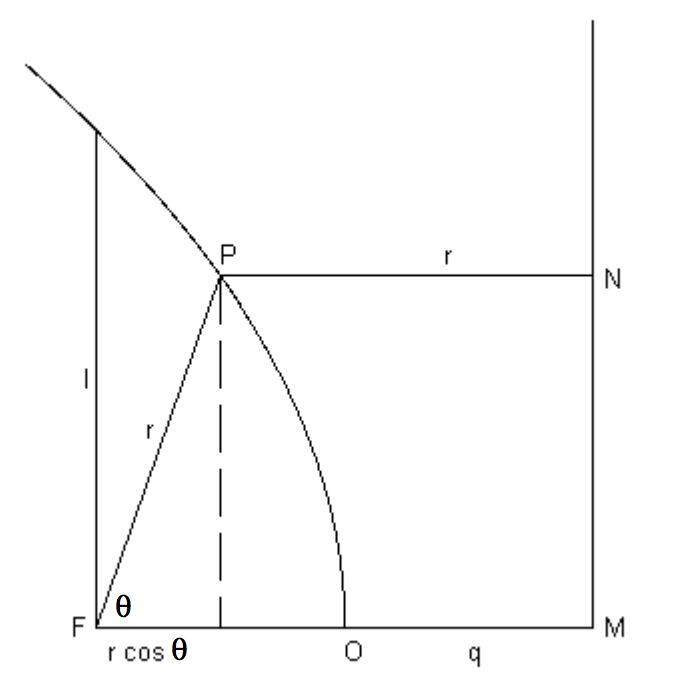
Як і у випадку з еліпсом, ми вибираємо фокус як полюс, а вісь параболи як початкову лінію. Орієнтуємо параболу так, щоб вершина була праворуч, як на малюнку$\text{II.27}$.

Згадуємо властивість focus-directrix,$\text{FP} = \text{PN}$. Також від визначення прямої кишки, так що$\text{FO}=\text{OM} = q$$\text{FM} = 2q = l$, довжина напівширокої прямої кишки. Тому відразу видно з малюнка$r \cos \theta + r = 2q = l$,$\text{II.27}$ що так, що полярне рівняння до параболи

$$r = \frac{l}{1+ \cos \theta}. \label{2.4.16}$$

$\text{FIGURE II.27}$

Це те саме, що і полярне рівняння до еліпса (Рівняння 2.3.36), з$e = 1$ параболою. Я дав різні похідні для еліпса та параболи; читач міг би поміняти два підходи та розробити рівняння 2.3.36 таким же чином, як ми розробили Рівняння$\ref{2.4.16}$.

Коли ми обговорюємо гіперболу, я попрошу вас показати, що її полярне рівняння також таке ж, як 2.3.36. Іншими словами, Рівняння 2.3.36 - це рівняння до конічного перерізу, і воно представляє еліпс, параболу або гіперболу відповідно до того, чи є$e<1, \ e=1 \ \text{or } e>1$.