2.2: Еліпс

Еліпс - це фігура, яку можна намалювати, встромивши дві шпильки в аркуш паперу, прив'язавши до шпильок довжину струни, натягнувши натягнуту олівцем струну і намалювавши отриману фігуру. Під час цього процесу сума двох відстаней від олівця до одного штифта і від олівця до іншого штифта залишається постійною і дорівнює довжині струни. Цей метод малювання еліпса дає нам формальне визначення, яке ми приймемо в цьому розділі, еліпса, а саме:

Еліпс - це локус точки, яка рухається таким чином, що сума її відстаней від двох нерухомих точок, які називаються вогнищами, є постійною (див. Рис. II.6).

\(\text{FIGURE II.6}\)

Назвемо суму цих двох відстаней (тобто довжини рядка)\(2a\). Ставлення відстані між осередками до довжини струни називається ексцентриситетом\(e\) еліпса, так що відстань між вогнищами дорівнює\(2ae\), і\(e\) є числом між 0 і 1.

Найдовша вісь еліпса - це його велика вісь, і трохи думки покаже, що його довжина дорівнює довжині рядка; тобто\(2a\). Найкоротша вісь - це незначна вісь, а її довжина зазвичай позначається\(2b\). Ексцентриситет пов'язаний із співвідношенням таким\(b/a\) чином, який ми коротко обговоримо.

Співвідношення

\[η = (a − b)/a\]

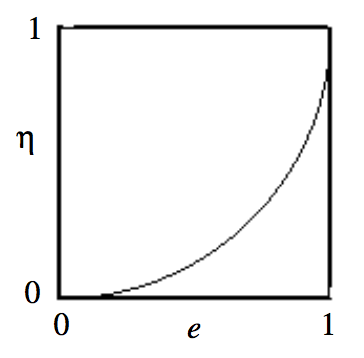
називається еліптичністю еліпса. Це лише альтернативна міра нециркулярності. Це пов'язано з ексцентриситетом, і ми отримаємо це відношення незабаром, теж. До цього часу\(\text{II.7}\) на малюнку зображено відношення між ними.

\(\text{FIGURE II.7}\)

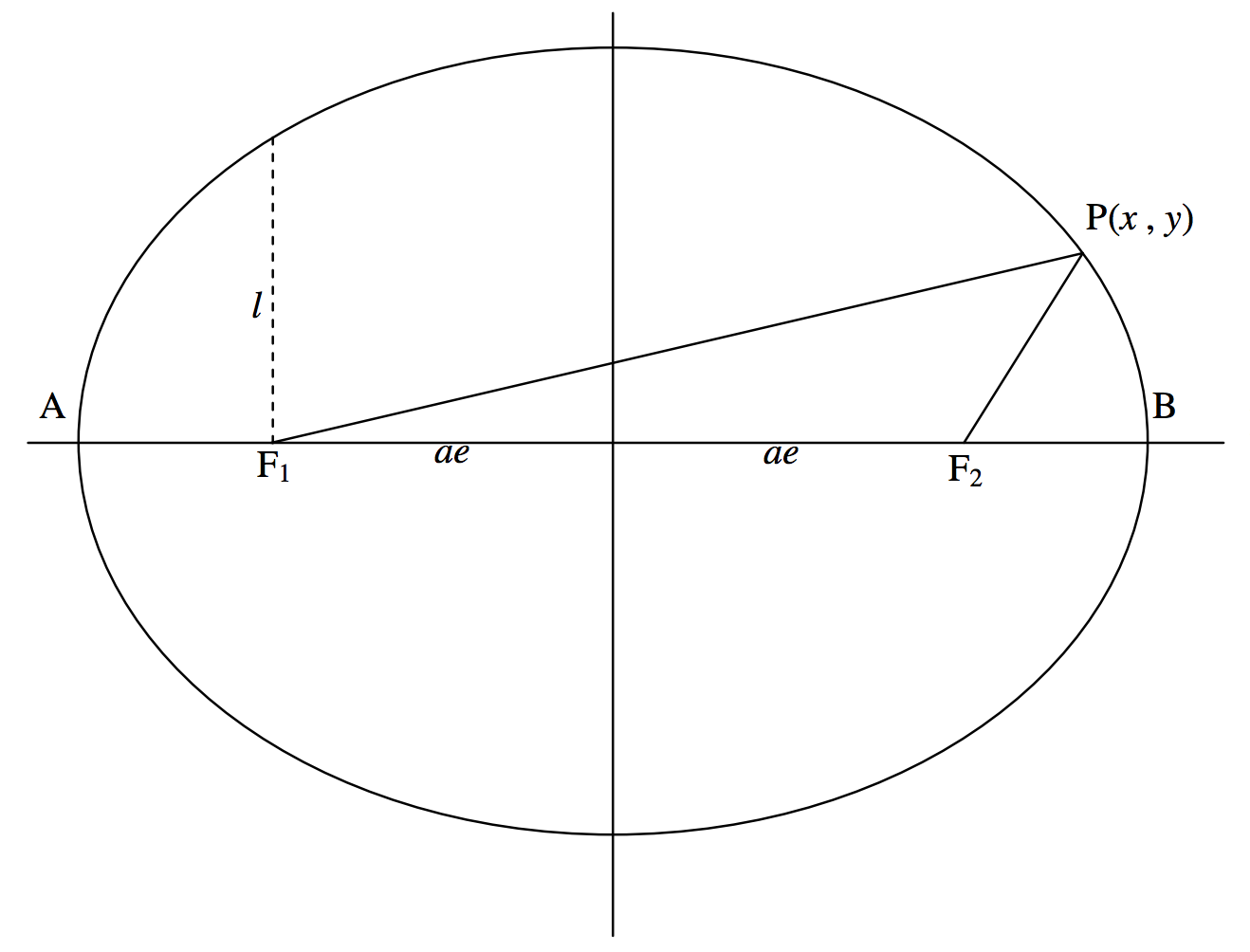
Ми використаємо наше визначення еліпса, щоб отримати його Рівняння в прямокутних координатах. Ми розмістимо два осередки на\(x\) осі -у координатах (−\(ae\), 0) та (\(ae\), 0) (див. Рис. II.8).

\(\text{FIGURE II.8}\)

Визначення цього вимагає\(\textbf{PF}_1 + \textbf{PF}_2 = 2a\). Тобто:

\[\left[ (x + ae)^2 + y^2 \right]^{\frac{1}{2}} + \left[ (x-ae)^2 + y^2 \right]^{\frac{1}{2}} = 2a, \label{2.3.1} \tag{2.3.1}\]

і це рівняння до еліпса. Читач повинен вміти, трохи трохи незручною алгебри, показати, що це можна написати зручніше, як

\[\frac{x^2}{a^2} + \frac{y^2}{a^2(1-e^2)} = 1 . \label{2.3.2} \tag{2.3.2}\]

Поставивши\(x = 0\), видно, що еліпс перетинає\(y\) -вісь на\(\pm a \sqrt{1-e^2}\) і, отже, що\(a \sqrt{1-e^2}\) дорівнює півмалій осі\(b\). Таким чином, ми маємо знайоме Рівняння до еліпса.

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.3.3} \tag{2.3.3}\]

а також важливе співвідношення між\(a\),\(b\) і\(e\):

\[b^2 = a^2 (1-e^2) \label{2.3.4} \tag{2.3.4}\]

Читач також тепер може вивести зв'язок між еліптичністю\(η\) та ексцентричністю\(e\):

\[η = 1 - \sqrt{(1-e^2)}. \label{2.3.5} \tag{2.3.5}\]

Це також може бути написано

\[e^2 = \sqrt{η(2-η)} \label{2.3.6} \tag{2.3.6}\]

або\[e^2 + (η -1)^2 = 1. \label{2.3.7} \tag{2.3.7}\]

Це показує, до речі, що графік\(η\) проти\(e\), який ми намалювали на малюнку\(\text{II.7}\), є частиною кола радіуса 1 по центру\(e = 0, \ η = 1\).

На малюнках\(\text{II.9}\) я намалював еліпси ексцентриситетів від 0,1 до 0,9 з кроком 0,1, а на малюнку\(\text{II.10}\) я намалював еліпси еліптичності від 0,1 до 0,9 з кроком 0,1. Ви можете виявити, що еліптичність дає вам краще уявлення, ніж ексцентриситет неокружності еліпса. Для вправи слід малювати в положеннях вогнищ кожного з цих еліпсів, і вирішити, чи дає ексцентриситет або еліптичність краще уявлення про «ексцентриситет» вогнищ. Відзначимо, що ексцентриситети орбіт Марса і Меркурія складають, відповідно, близько 0,1 і 0,2 (це самі ексцентричні з планетарних орбіт крім комет Плутона), і оку важко помітити, що вони взагалі відходять від кіл - хоча, коли осередки намальовані, очевидно що вогнища «екс-центричні».

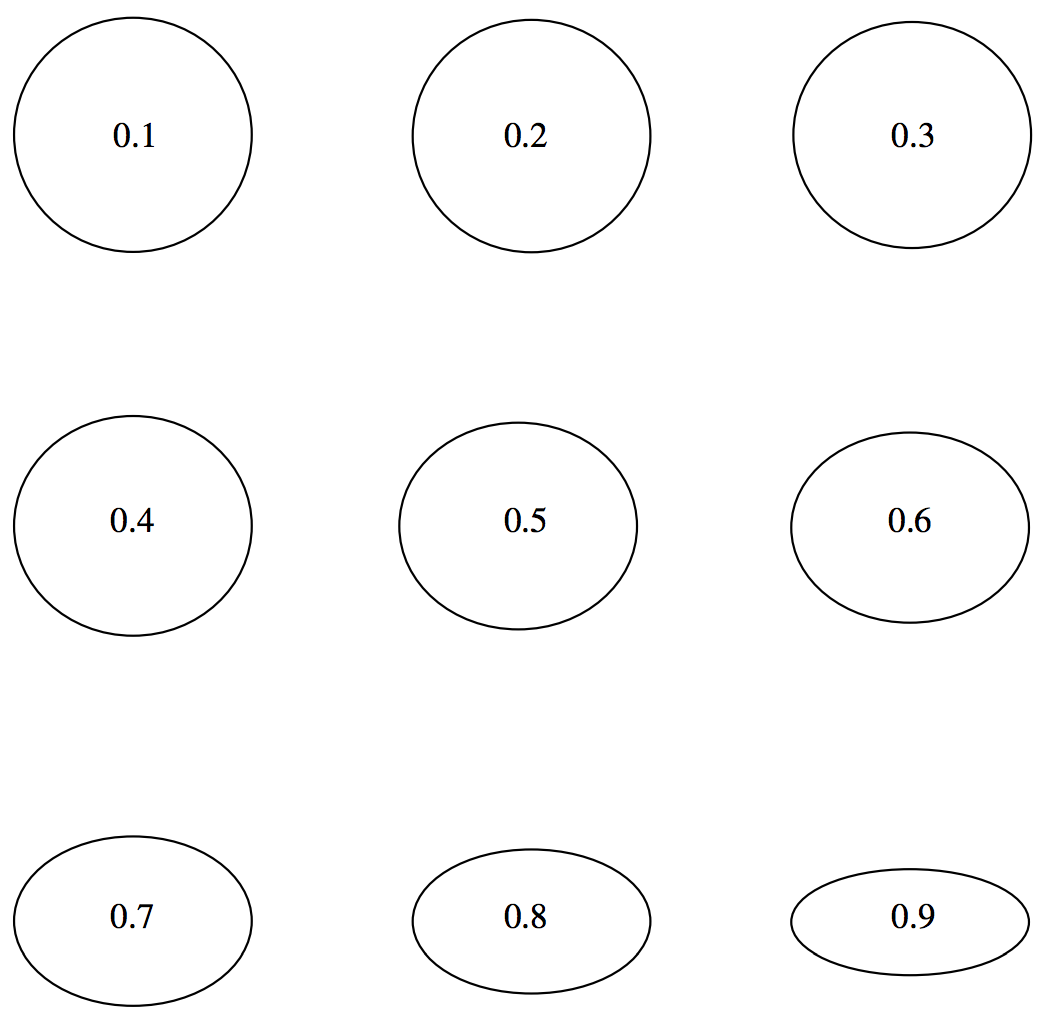
\(\text{FIGURE II.9}\): Число всередині кожного еліпса - це його ексцентриситет.

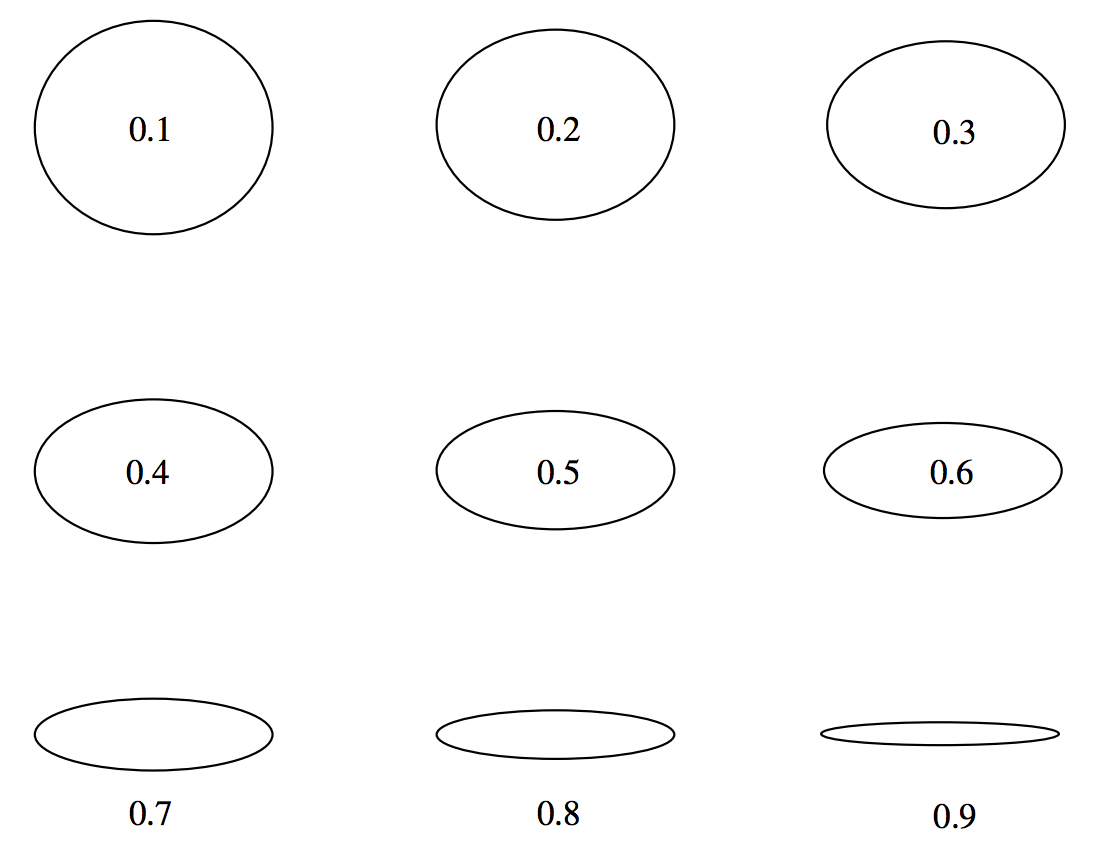
\(\text{FIGURE II.10}\): Фігура всередині або під кожним еліпсом - це його еліптичність.

У теорії планетарних орбіт Сонце буде знаходитися в одному фокусі. Припустимо, що це буде на\(\text{F}_2\) (див. Малюнок\(\text{II.8}\)). У цьому випадку відстань\(\text{F}_2 \ \text{B}\) дорівнює перигелієвій відстані\(q\), і дорівнює

\[q = a(1-e). \label{2.3.8} \tag{2.3.8}\]

Відстань\(\text{F}_2 \ \text{A}\) - це афелійна відстань Q (деякими вимовляється афелієм та афелієм іншими - і обидва мають захисні позиції), і вона дорівнює

\[Q = a(1 + e). \label{2.3.9} \tag{2.3.9}\]

Лінія, паралельна малій осі і проходить через вогнище, називається широкою прямою кишкою (множина: latera recta). Довжина semi latus прямої кишки зазвичай позначається\(l \) (іноді шляхом\(p\)). Його довжина отримується шляхом введення\(x = ae\) рівняння до еліпса, і буде легко виявлено, що

\[l = a(1-e^2). \label{2.3.10} \tag{2.3.10}\]

Довжина прямої кишки semi latus є важливою величиною в теорії орбіти. Буде встановлено, наприклад, що енергія планети тісно пов'язана з напівпровідною віссю\(a\) її орбіти, тоді як її кутовий імпульс тісно пов'язаний з напівстатевої прямої кишки.

Коло, діаметр якого є великою віссю еліпса, називається ексцентриковим колом або, бажано, допоміжним колом (фігурою\(\text{II.11}\)). Його рівняння

\[x^2 + y^2 = a^2 . \label{2.3.11} \tag{2.3.11}\]

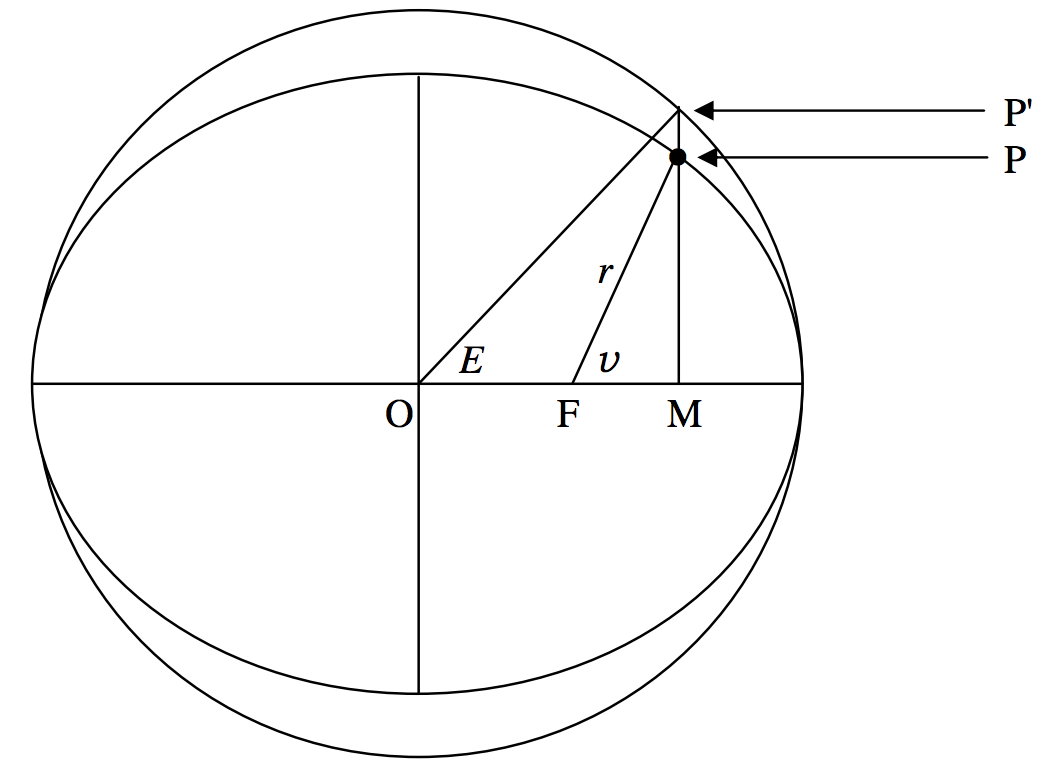
\(\text{FIGURE II.11}\)

В теорії орбіти кут\(v\) (позначається деякими\(f\) авторами) називається справжньою аномалією планети на її орбіті. Кут\(E\) називається ексцентричної аномалією, і важливо знайти зв'язок між ними.

Спочатку зауважимо, що, якщо ексцентрична аномалія є\(E\), абсциси\(\text{P}^\prime\) і з\(\text{P}\) є кожною\(a \cos E\). Ордината\(\text{P}^\prime\) є\(a \sin E\). Поставивши\(x = a \cos E\) в Рівняння до еліпса, ми відразу виявляємо, що ордината\(\text{P}\) є\(b \sin E\). Далі слід кілька відрахувань. Одна з них полягає в тому, що будь-яка точка, абсциса та ордината якої мають форму

\[x = a \cos E , \quad y = b \sin E \label{2.3.12} \tag{2.3.12}\]

знаходиться на еліпсі напіввеликої\(a\) осі та напівмалої осі\(b\). Ці два рівняння можна розглядати як параметричні рівняння до еліпса. Їх можна використовувати для опису еліпса так само легко, як

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.3.13} \tag{2.3.13}\]

і справді це рівняння\(E\) - елімінатор параметричних рівнянь.

Співвідношення\(\text{PM}/\text{P}^\prime \text{M}\) для будь-якої лінії, перпендикулярної до великої осі, дорівнює\(b/a\). Отже, площа еліпса в\(b/a\) рази перевищує площу допоміжного кола; а оскільки площа допоміжного кола є\(\pi a^2\), то випливає, що площа еліпса є\(\pi ab\).

На малюнку\(\text{II.11}\) відстань\(r\) називається вектором радіуса (векторами радіусів множини), а з теореми Піфагора його довжина задається

\[r^2 = b^2 \sin^2 E + a^2 (\cos E - e)^2 . \label{2.3.14} \tag{2.3.14}\]

Замінюючи\(\sin^2 E\) і\(1 − \cos^2 E\)\(a^2 (1 - e^2 )\) для\(b^2\), ми незабаром виявимо, що

\[r = a (1 - e \cos E ) \label{2.3.15} \tag{2.3.15}\]

Потім відразу випливає, що бажане співвідношення між\(v\) і\(E\) є

\[\cos v = \frac{\cos E - e}{1 - e \cos E} . \label{2.3.16} \tag{2.3.16}\]

З тригонометричних ідентичностей це також можна записати

\[\sin v = \frac{\sqrt{1-e^2} \sin E}{1-e \cos E} \tag{2.3.17a} \label{2.3.17a}\]

або\[\tan v = \frac{\sqrt{1-e^2} \sin E}{\cos E - e} \label{2.3.17b} \tag{2.3.17b}\]

або\[ \tan \frac{1}{2} v = \sqrt{\frac{1+e}{1-e}} \tan \frac{1}{2} E . \label{2.3.17c} \tag{2.3.17c}\]

Також можуть бути корисні зворотні формули:

\[\cos E = \frac{e+\cos v}{1+e \cos v} \label{2.3.17d} \tag{2.3.17d}\]

\[\sin E = \frac{\sin v \sqrt{1-e^2}}{e + \cos v} \label{2.3.17e} \tag{2.3.17e}\]

\[\tan E = \frac{\sin v \sqrt{1-e^2}}{e+ \cos v} \label{2.3.17f} \tag{2.3.17f}\]

\[\tan \frac{1}{2} E = \sqrt{\frac{1-e}{1+e}} \tan \frac{1}{2} v . \label{2.3.17g} \tag{2.3.17g}\]

Існує ряд різних геометричних властивостей еліпса, деякі, але не обов'язково всі, з яких можуть виявитися корисними в орбітальних розрахунках. Деякі з них ми опишемо в наступному.

Дотичні до еліпса

Знайдіть, де пряма\(y = mx + c\) перетинає еліпс

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 . \label{2.3.18} \tag{2.3.18}\]

Відповідь на це питання можна знайти, підставивши\(mx + c\)\(y\) в Рівняння на еліпс. Після деякої перестановки, квадратне рівняння в\(x\) результаті:

\[\left(a^2 m^2 + b^2 \right) x^2 + 2a^2 cmx + a^2 \left( c^2 - b^2 \right) = 0 . \label{2.3.19} \tag{2.3.19}\]

Якщо це рівняння має два дійсних кореня, коріння\(x\) - це координати двох точок, де лінія перетинає еліпс. Якщо він не має справжніх коренів, лінія пропускає еліпс. Якщо він має два збігаються реальних кореня, лінія дотична до еліпса. Умова для цього знаходить шляхом встановлення дискримінанту квадратного рівняння в нуль, з якого встановлено, що

\[c^2 = a^2 m^2 + b^2 . \label{2.3.20} \tag{2.3.20}\]

Таким чином, пряма лінія форми

\[y = mx \pm \sqrt{a^2 m^2 + b^2} \label{2.3.21} \tag{2.3.21}\]

дотична до еліпса.

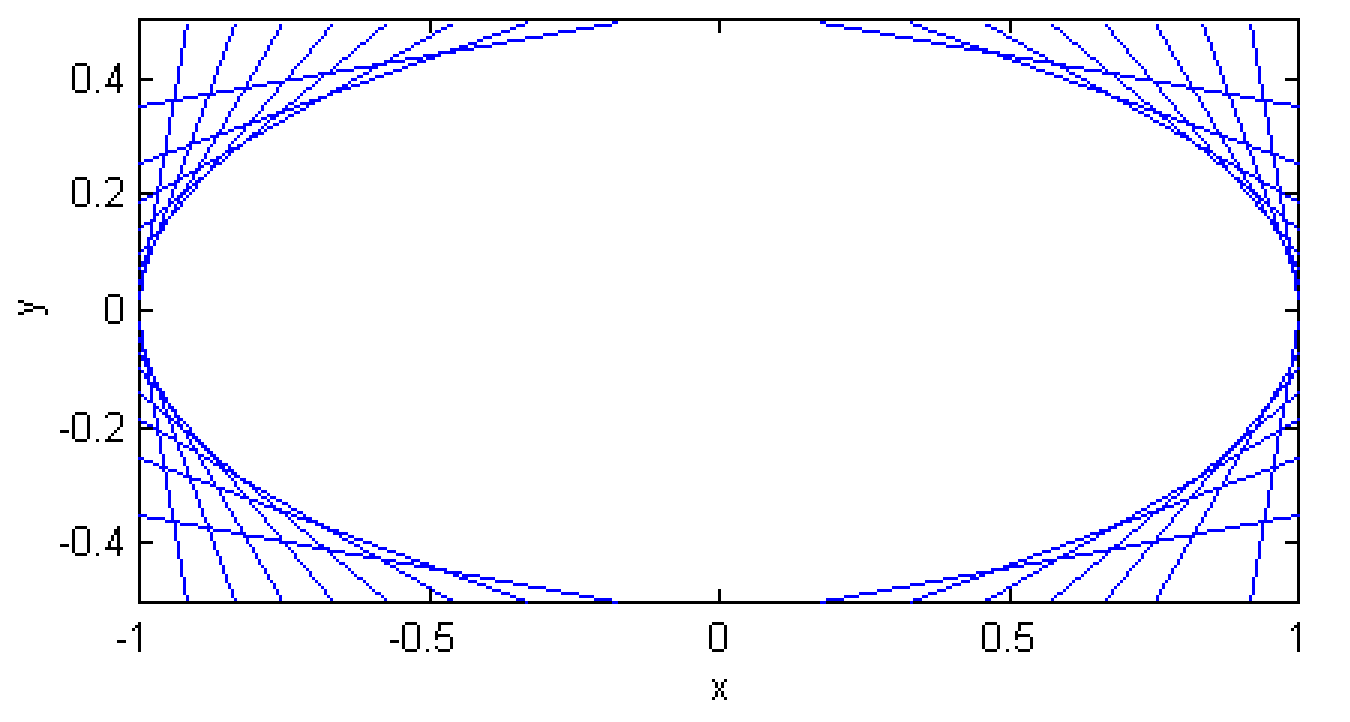
\(\text{II.12}\)На малюнку зображено кілька таких ліній, для\(a = 2b\) і\(\tan^{-1} \ m)\) нахилів (від\(0^\circ\) до\(180^\circ\) з кроком\(10^\circ\)

\(\text{FIGURE II.12}\)

Коло режисера

Рівняння, яке ми щойно вивели для дотичної до еліпса, можна переставити на читання

\[m^2 \left( a^2 - x^2 \right) + 2mx + b^2 - y^2 = 0. \label{2.3.22} \tag{2.3.22} \]

Тепер добуток нахилів двох ліній, які знаходяться під прямим кутом один до одного, є\(−1\) (Рівняння 2.2.17). Тому, якщо ми замінимо\(m\) у наведеному вище Рівняння на,\(−1/m\) ми отримаємо ще одну дотичну до еліпса, під прямим кутом до першого. Рівняння до цієї другої дотичної стає (після множення на\(m\))

\[m^2 \left( b^2 - y^2 \right) - 2mx + a^2 - x^2 = 0. \label{2.3.23} \tag{2.3.23}\]

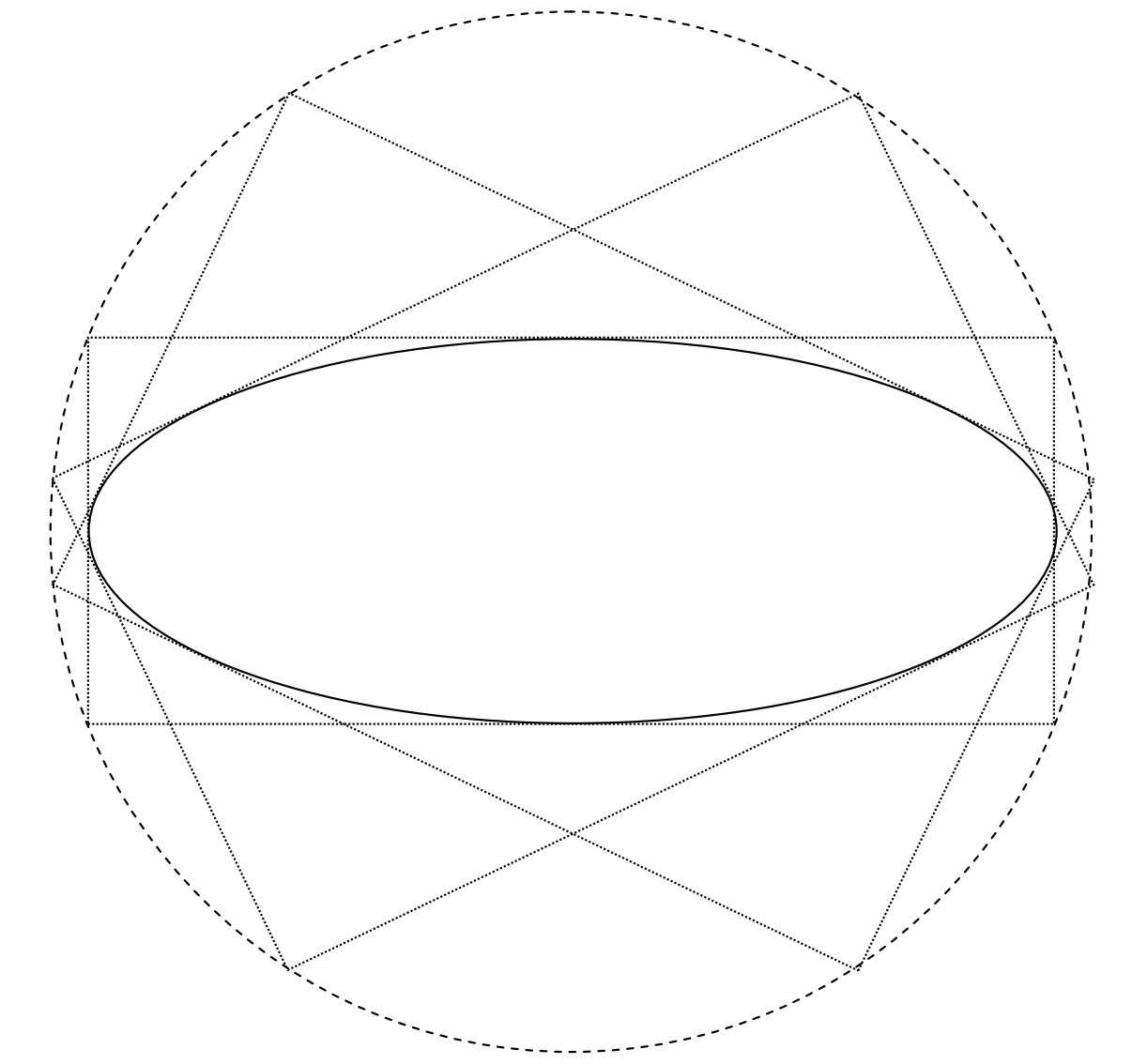
Якщо ми усунемо\(m\) з цих двох рівнянь, ми отримаємо рівняння в\(x\),\(y\) яке описує точку, де зустрічаються два перпендикулярні тангенси; тобто рівняння, яке опише криву, яка є локусом точки перетину двох перпендикулярних тангенсів. Виходить, що ця крива є окружністю радіуса\(\sqrt{a^2 + b^2}\), і називається вона директорським колом.

Це простіше, ніж може здатися спочатку усунути\(m\) з Рівняння. Ми просто повинні додати рівняння\(\ref{2.3.22}\) і\(\ref{2.3.23}\):

\[m^2 \left( a^2 + b^2 - x^2 - y^2 \right) + a^2 + b^2 - x^2 - y^2 = 0 . \label{2.3.24} \tag{2.3.24}\]

По-справжньому\(m\), це може бути тільки в тому випадку, якщо

\[x^2 + y^2 = a^2 + b^2 , \label{2.3.25} \tag{2.3.25}\]

який є необхідним локусом окружності директора радіуса\(\sqrt{a^2 + b^2}\). Вона проілюстрована на малюнку\(\text{II.13}\).

Тепер ми виведемо рівняння до лінії, яка є дотичною до еліпса в точці\((x_1 , \ y_1 )\).

\((x_1 , \ y_1 ) = (a \cos E_1 , b \sin E_1 )\)\((x_2 , \ y_2 ) = (a \cos E_2 , b \sin E_2 )\)Дозволяти і бути дві точки на еліпсі.

Лінія, що з'єднує ці дві точки

\[\frac{y-b\sin E_1}{x-a \cos E_1} = \frac{b ( \sin E_2 - \sin E_1 )}{a(\cos E_2 - \cos E_1 )} = \frac{2b \cos \frac{1}{2}(E_2 + E_1) \sin \frac{1}{2}(E_2 - E_1)}{-2a \sin \frac{1}{2} (E_2 + E_1) \sin \frac{1}{2}(E_2 - E_1)} = -\frac{b \cos \frac{1}{2} (E_2 + E_1)}{a \sin \frac{1}{2} (E_2 + E_1)}. \label{2.3.26} \tag{2.3.26}\]

\(\text{FIGURE II.13}\)

Тепер давайте\(E_2\) наблизитися\(E_1\), врешті-решт збігаючись з ним. Отримане рівняння

\[\frac{y-b\sin E}{x - a \cos E} = - \frac{b \cos E}{a \sin E} , \label{2.3.27} \tag{2.3.27}\]

в якому ми більше не розрізняємо\(E_1\) і\(E_2\), є Рівняння прямої, яка є дотичною до еліпса в\((a \cos E \ , b \sin E )\). Це можна написати

\[\frac{x \cos E}{a} + \frac{y \sin E}{b} = 1 \label{2.3.28} \tag{2.3.28}\]

або, з точки зору\((x_1 , \ y_1 )\),

\[\frac{x_1 x}{a^2} + \frac{y_1 y}{b^2} = 1, \label{2.3.29} \tag{2.3.29}\]

яка є дотичною до еліпса в\((x_1 , \ y_1 )\).

Цікава властивість дотичної до еліпса, доказ якого я залишаю читачеві, полягає в тому, що\(\text{F}_1 \text{P}\) і\(\text{F}_2 \text{P}\) зробити рівні кути з дотичною в\(\text{P}\). Якби внутрішня частина еліпса була дзеркалом, що відбиває\(\text{F}_1\), а точкове джерело світла було б розміщено на\(\text{F}_2\). (Подивіться на фігуру\(\text{II.6}\) або\(\text{II.8}\).) Це мало цікаве медичне застосування. У пацієнта є камінь в нирках. Пацієнта просять полежати в еліптичній ванні, з нирковим каменем при\(\text{F}_2\). Невеликий вибух детонується при\(\text{F}_1\); вибухонебезпечна звукова хвиля, що\(\text{F}_1\) виходить з, фокусується як імплозія на\(\text{F}_2\) і нирковий камінь при\(\text{F}_2\) руйнується. Не намагайтеся це вдома.

Директори

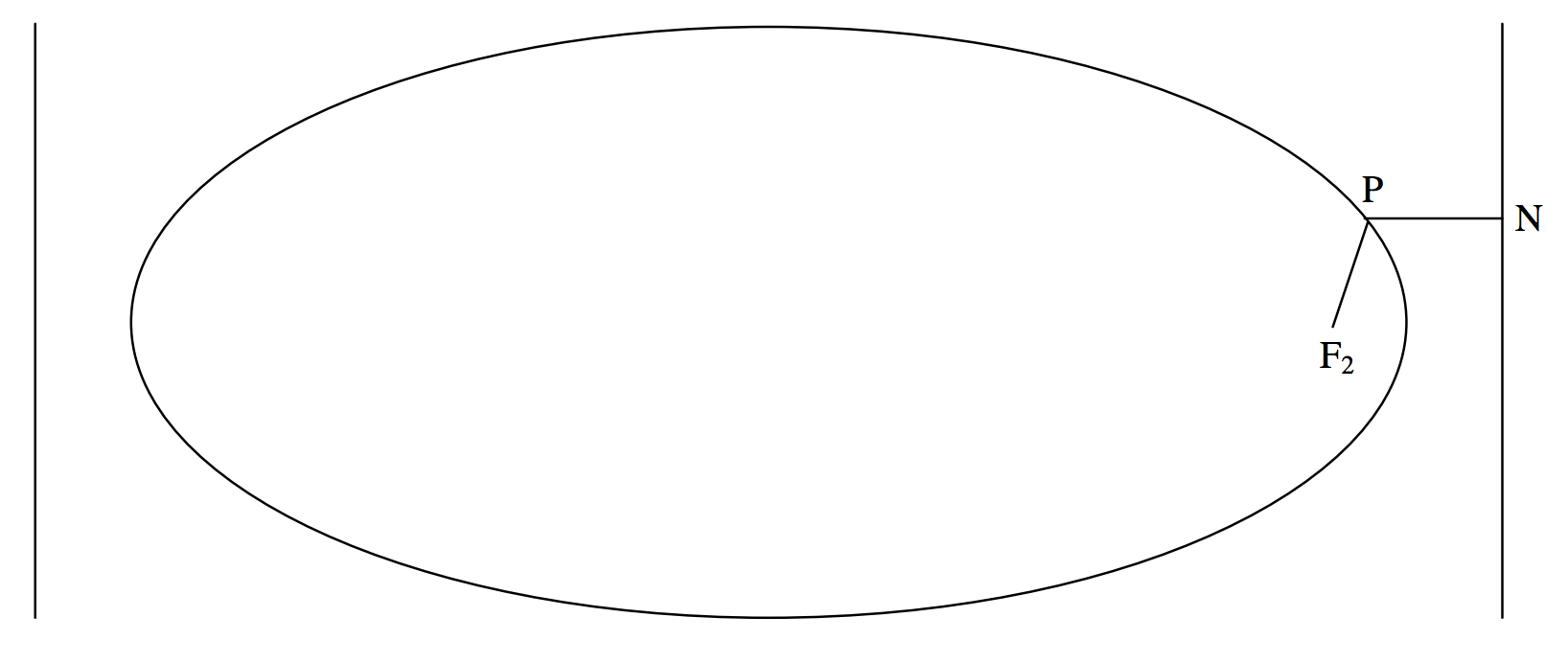
Дві лінії\(x = \pm a / e\) називаються директрисами (одниною директрисою) еліпса (фігура\(\text{II.14}\)).

\(\text{FIGURE II.14}\)

Еліпс має властивість, що для будь-якої точки\(\text{P}\) на еліпсі відношення відстані\(\text{PF}_2\) до фокусу до відстані\(\text{PN}\) до директриси є постійним і дорівнює ексцентриситету еліпса. Дійсно, ця властивість іноді використовується як визначення еліпса, і всі Рівняння і властивості, які ми маємо до сих пір похідні, можна вивести з такого визначення. Ми, однак, прийняли інше визначення, і властивість focus-directrix повинна бути виведена. Це просто, бо, (нагадуючи, що абциса\(\text{F}_2\) є\(ae\)) ми бачимо з малюнка\(\text{II.14}\), що квадрат потрібного співвідношення є

\[\frac{(x - a e)^2 + y^2}{(a/e-x)^2}. \label{2.3.30} \tag{2.3.30}\]

Про заміну

\[b^2 \left( 1 - \left( \frac{x}{a} \right)^2 \right) = a^2 \left( 1 - e^2 \right) \left( 1 - \left( \frac{x}{a} \right)^2 \right) = \left( 1 - e^2 \right) \left( a^2 - x^2 \right) \label{2.3.31} \tag{2.3.31}\]

бо\(y^2\), наведене вище вираз, як видно, звести до\(e^2\).

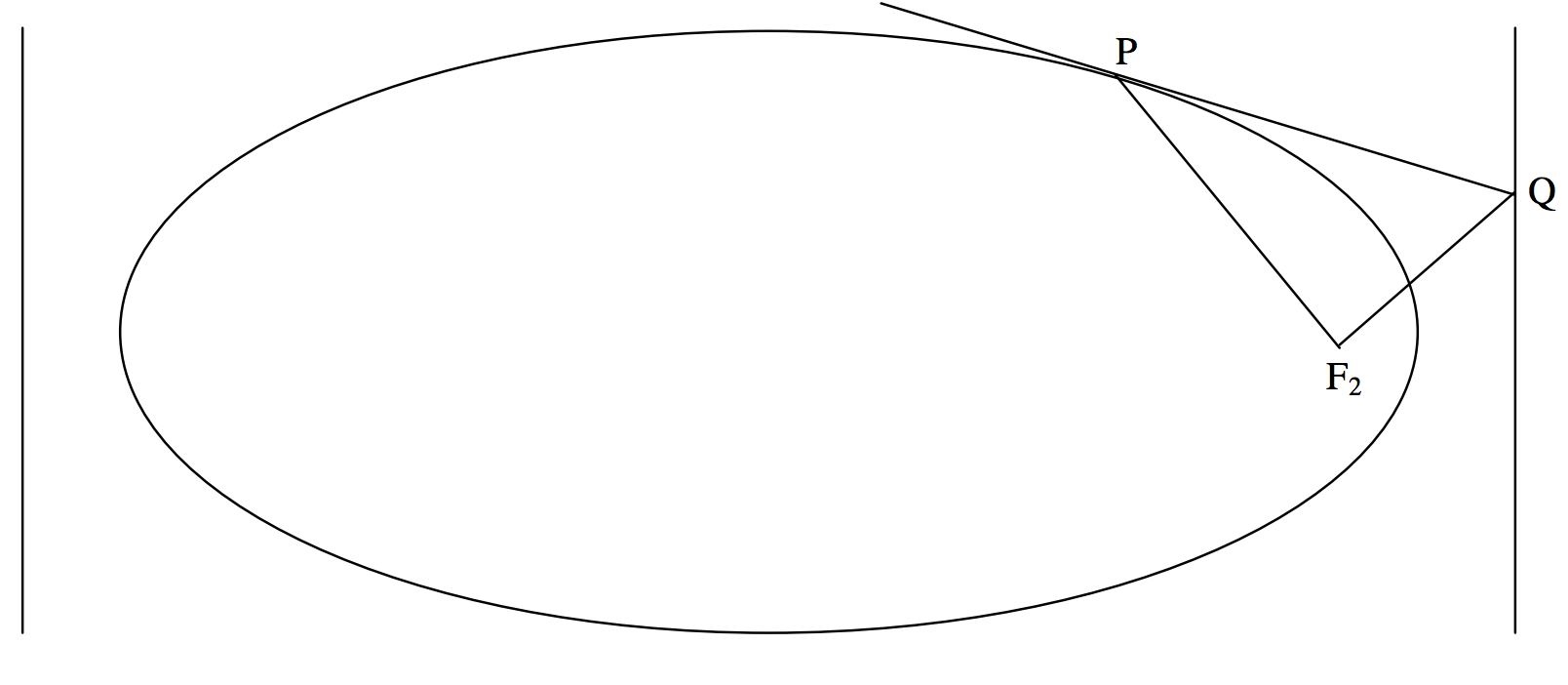
Ще одна цікава властивість фокусу та директриси, хоча властивість, ймовірно, не має великого застосування до теорії орбіти, полягає в тому, що якщо дотична до еліпса в точці\(\text{P}\) перетинає директрису в\(\text{Q}\), то\(\text{P}\) і\(\text{Q}\) субтенд прямий кут у фокусі. (Див. Малюнок\(\text{II.15}\)).

\(\text{FIGURE II.15}\)

Таким чином, тангенс\(\text{P} = (x_1 , \ y_1 )\) при

\[\frac{x_1 x}{a^2} + \frac{y_1 y }{b^2} = 1 \label{2.3.32} \tag{2.3.32}\]

і це просто показати, що вона перетинає директрису\(x = a/e\) в точці

\[\left( \frac{a}{e} , \frac{b^2}{y_1} \left( 1 - \frac{x_1}{ae} \right) \right) . \]

Координати фокусу\(\text{F}_2\) є\((ae, 0)\). Нахил лінії\(\text{PF}_2\) є,\((x_1 - ae )/y_1\) а нахил лінії\(\text{QF}_2\) дорівнює

\[\frac{\frac{b^2}{y_1} \left( 1 - \frac{x_1}{ae} \right)}{\frac{a}{e} - ae}. \]

Легко показати, що твір цих двох схилів є\(−1\), а значить, що\(\text{PF}_2\) і\(\text{QF}_2\) знаходяться під прямим кутом.

Сполучених діаметрів

Ліва рука малюнка\(\text{II.16}\) показує коло і два перпендикулярних діаметра. На малюнку правої руки показано, як виглядатиме коло при погляді під деяким косим кутом. Коло стало еліпсом, а діаметри вже не перпендикулярні. Діаметри називаються сполученими діаметрами еліпса. Один сполучений з іншим, а інший - сполучений з одним. Вони мають властивість - або визначення - що кожна бісекція всіх хорд паралельно іншій, оскільки ця властивість бісекції, яка, очевидно, утримується перпендикулярними діаметрами кола, незмінна в проекції.

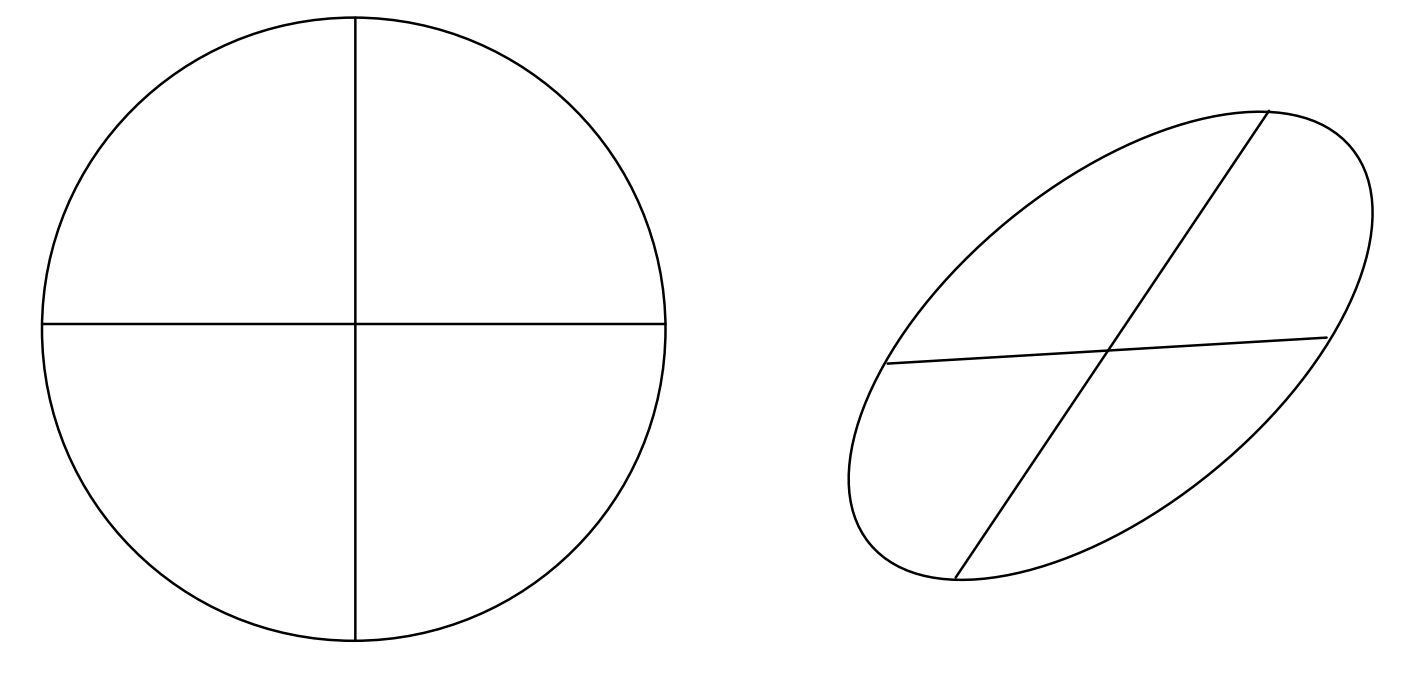
\(\text{FIGURE II.16}\)

Легко намалювати два сполучені діаметри еліпса ексцентриситету\(e\) або скориставшись цією останньою згаданою властивістю, або зазначивши, що добуток нахилів двох сполучених діаметрів є\(e^2 − 1\). Доказ цього залишається для задоволення читача.

Проблема сходів.

Жодна книга з елементарної прикладної математики не обходиться без проблеми сходів. Сходи довжиною\(a + b\) спирається на гладку вертикальну стіну і рівний горизонтальний підлогу. Конкретна сходинка знаходиться на відстані\(a\) від верхньої частини сходів і\(b\) знизу сходів. Покажіть, що, коли сходи ковзає, сходинка описує еліпс. (Цей результат підкаже інший спосіб малювання еліпса.) Див\(\text{II.17}\). Малюнок.

\(\text{FIGURE II.17}\)

Якщо ви не зробили цю проблему через одну хвилину, ось підказка. Нехай кут, який робить сходи з підлогою, в будь-який момент буде\(E\). Ось і закінчується підказка.

Читач може знати, що деякі геометричні властивості, які ми обговорювали в останніх кількох параграфах, більше представляють рекреаційний інтерес і можуть не мати великого прямого застосування в теорії орбіт. У наступному підрозділі ми повертаємося до властивостей і рівнянь, які дуже актуальні для орбітальної теорії - мабуть, найважливіше з усіх для розуміння комп'ютера орбіти.

Полярне рівняння до еліпса

Ми отримаємо рівняння в полярних координатах до еліпса, фокусом якого є полюс полярних координат, а велика вісь якого - початкова лінія\((\theta = 0^\circ )\) полярних координат. На малюнку\(\text{II.18}\) ми вказали кут\(\theta\) полярних координат, і читачеві може виникнути думка, що ми раніше використовували символ\(v\) для цього кута і називали його справжньою аномалією. Дійсно в даний час\(v\) і\(\theta\) ідентичні, але трохи пізніше ми розберемо їх між собою.

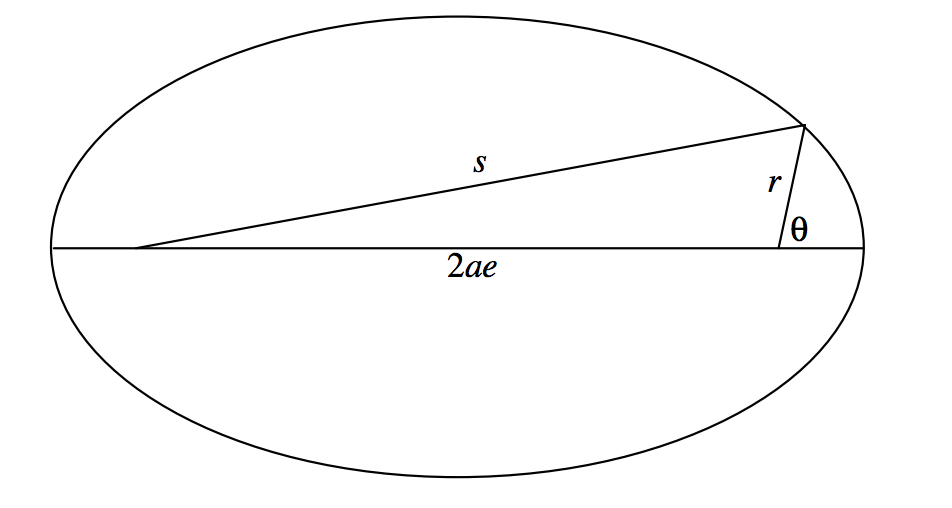
\(\text{FIGURE II.18}\)

З нашого визначення еліпса\(s = 2a − r\), і так

\[s^2 = 4a^2 - 4ar + r^2 . \label{2.3.33} \tag{2.3.33}\]

З формули косинуса для плоского трикутника

\[s^2 = 4a^2 e^2 + r^2 + 4aer \cos \theta . \label{2.3.34} \tag{2.3.34}\]

Про прирівнювання цих виразів ми незабаром отримаємо

\[a \left( 1 - e^2 \right) = r \left( 1 + e \cos \theta \right) . \label{2.3.35} \tag{2.3.35} \]

Ліва сторона дорівнює підлозі прямої кишки\(l\), і тому ми приходимо до полярного рівняння до еліпса, фокусуємося як полюс, велика вісь як початкова лінія:

\[r = \frac{1}{1+e \cos \theta}. \label{2.3.36} \tag{2.3.36}\]

Якщо велика вісь нахилена під кутом\(ω\) до початкової лінії (малюнка\(\text{II.19}\)), рівняння стає

\[r = \frac{l}{1 + e \cos (\theta - ω)} = \frac{l}{1+ e \cos v}. \label{2.3.37} \tag{2.3.37}\]

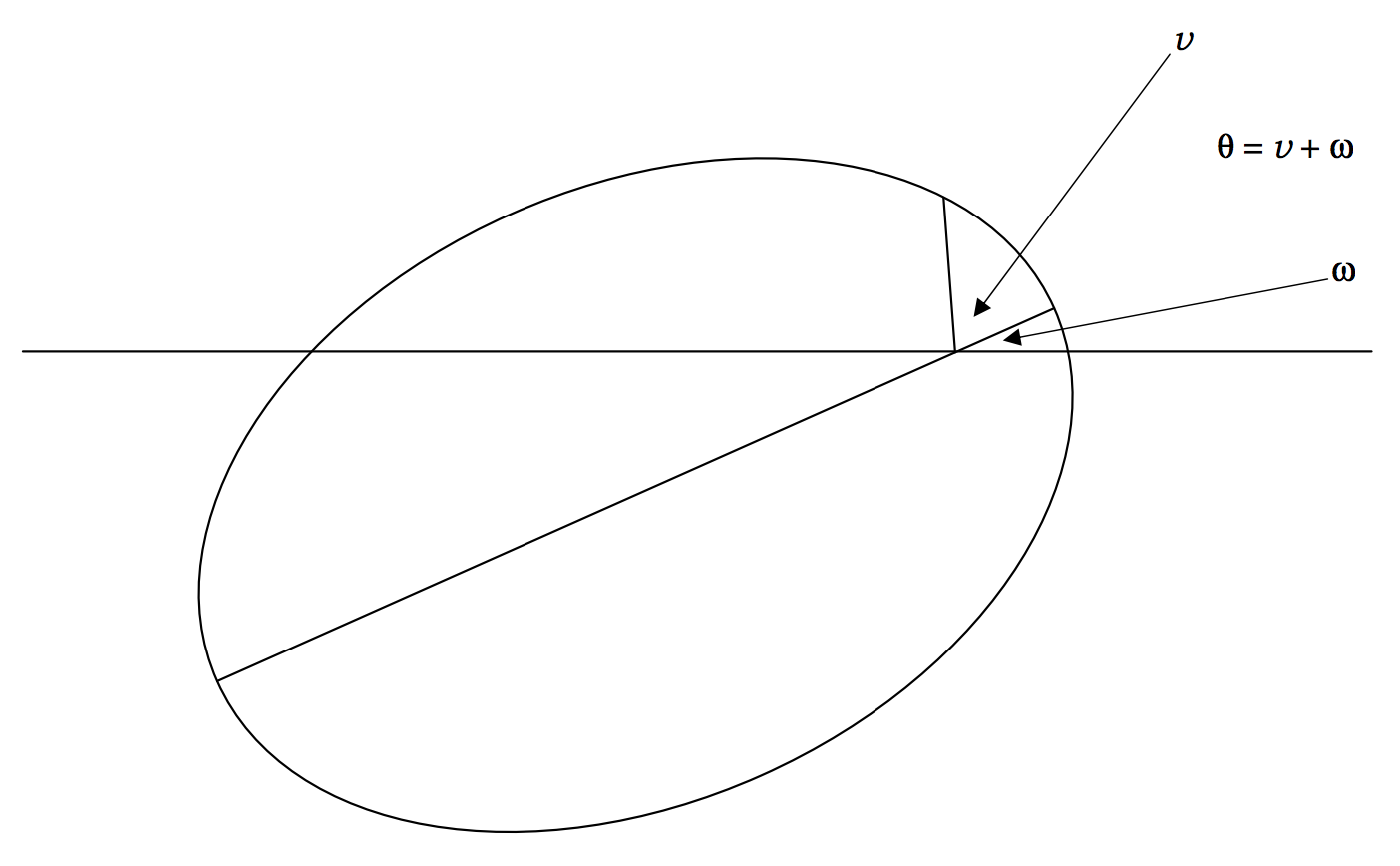
\(\text{FIGURE II.19}\)

Різниця між\(θ\) і\(v\) зараз очевидна. \(θ\)кут полярних\(ω\) координат, кут між великою віссю і початковою лінією (\(ω\)буде називатися в орбітальної теорії як «аргумент перигелія»), і\(v\), справжня аномалія, - кут між вектором радіуса і початковою лінією.