2.1: Пряма лінія

Можна подумати, що існує досить обмежена кількість, яка може бути написана про геометрію прямої лінії. Однак ми можемо керувати кількома рівняннями тут (у цьому розділі є 35 на прямій лінії), і ми повернемося для отримання додаткової інформації про цю тему в розділі 4.

Більшість читачів будуть знайомі з рівнянням для прямої лінії:

\[y = mx + c \label{2.2.1} \tag{2.2.1}\]

Нахил (або градієнт) лінії, яка є тангенсом кута, який він робить з\(x\) -віссю, є\(m\), а перехоплення на\(y\) -осі є\(c\). Існують різні інші форми, які можуть бути корисними, наприклад

\[\frac{x}{x_0} + \frac{y}{y_0} = 1 \label{2.2.2} \tag{2.2.2}\]

\[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1} \label{2.2.3} \tag{2.2.3}\]

які також можуть бути написані

\ begin {масив} {| c c | c}
x & y &
1\\ x_1 & y_1 & 1 & =0\
x_2 & y_2 & 1
\\\ мітка {2.2.4}
\ кінець {масив}

\[x \cos \theta + y \sin \theta = p \label{2.25} \tag{2.2.5}\]

Чотири форми проілюстровані на малюнку\(\text{II.1}\).

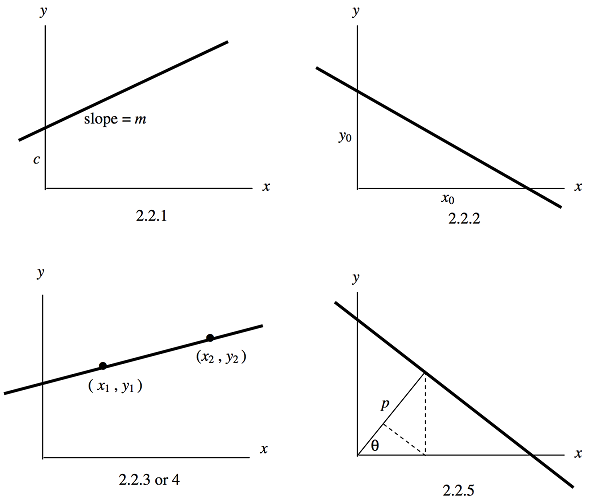
\(\text{FIGURE II.1}\)

Пряма лінія також може бути написана у вигляді

\[Ax + By + C = 0. \label{2.2.6} \tag{2.2.6}\]

Якщо\(C = 0\), лінія проходить через початок. Якщо\(C ≠ 0\), інформація не втрачається, а якась арифметика і алгебра збережені, якщо розділити Equation\ ref {2.2.6} на\(C\) і перепишемо його у вигляді

\[ax + by = 1. \label{2.2.7} \tag{2.2.7}\]

\(P (x , y)\)Дозволяти точка на лінії і\(P_0 (x_0 , y_0 )\) нехай точка в площині не обов'язково на лінії. Цікаво знайти перпендикулярну відстань між\(P_0\) і лінією. \(S\)Дозволяти бути квадратом відстані між\(P_0\) і\(P\). Тоді

\[S = (x-x_0)^2 + (y-y_0)^2 \label{2.2.8} \tag{2.2.8}\]

Ми можемо висловити це через одиничну змінну\(x\) шляхом підстановки на\(y\) з Рівняння\(\ref{2.2.7}\). Диференціація по\(S\) відношенню до\(x\) буде потім показати,\(S\) що найменше для

\[x = \frac{a+b(bx_0 - ay_0)}{a^2 + b^2} \label{2.2.9} \tag{2.2.9}\]

Відповідне значення для\(y\), знайдене з Рівняння\(\ref{2.2.7}\) і\(\ref{2.2.9}\), дорівнює

\[y = \frac{b+a(ay_0 - bx_0)}{a^2 + b^2}. \label{2.2.10} \tag{2.2.10}\]

Точка\(\text{P}\) описується рівняннями\(\ref{2.2.9}\) і\(\ref{2.2.10}\) є найближчою точкою до\(\text{P}_0\) лінії. Перпендикулярна відстань\(\text{P}\) від лінії дорівнює\(p = √S\) або

\[p = \frac{1-ax_0 - by_0}{\sqrt{a^2+b^2}}. \label{2.2.11} \tag{2.2.11}\]

Це позитивне, якщо\(\text{P}_0\) знаходиться на тій же стороні лінії, що і початок, і негативним, якщо він знаходиться на протилежній стороні. Якщо перпендикулярні відстані двох точок від прямої, розраховані з Рівняння\(\ref{2.2.11}\), мають протилежні знаки, вони знаходяться на протилежних сторонам прямої. Якщо\(p = 0\), або дійсно, якщо чисельник Рівняння\(\ref{2.2.11}\) дорівнює нулю, точка\(\text{P}_0 (x_0 , y_0 )\), звичайно, на прямій.

\(\text{A}(x_1 , y_1 ), \ \text{B}(x_2 , y_2 )\)\(\text{C}(x_3 , y_3 )\)Дозволяти і бути три точки в площині. Яка площа трикутника\(\text{ABC}\)? Один із способів відповісти на це пропонує малюнок\(\text{II.2}\).

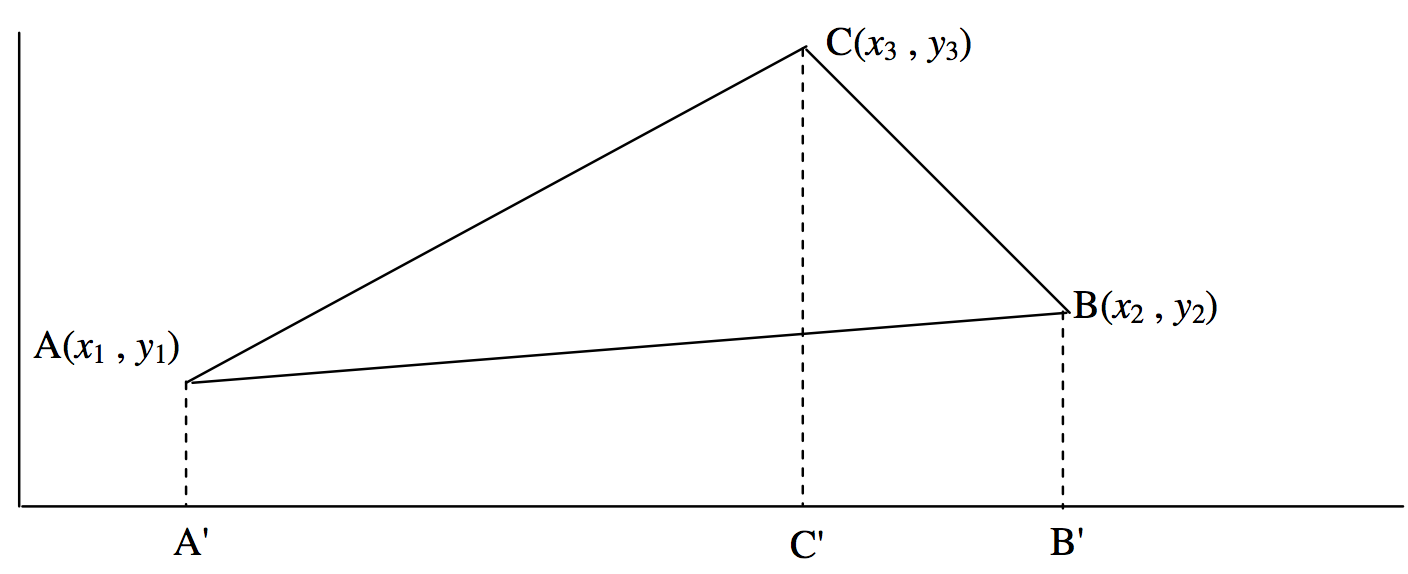
\(\text{FIGURE II.2}\)

Ми бачимо, що

площа трикутника\(\text{ABC}\) = площа трапеції\(\text{A}^\prime \text{ACC}^\prime\) (див. коментар*)
+ площа трапеції\(\text{C}^\prime \text{CBB}^\prime\)
− площа трапеції\(\text{A}^\prime \text{ABB}^\prime\).

\[ = \frac{1}{2} (x_3 - x_1) (y_3 + y_1) + \frac{1}{2} (x_2 - x_3)(y_2 + y_3) - \frac{1}{2} (x_2 - x_1) (y_2 + y_1) \]
\[ = \frac{1}{2} [x_1(y_2 - y_3) + x_2 (y_3 -y_1) + x_3(y_1 - y_2)]\]

\ begin {масив} {l r | c c c |}
& x_1 & x_2 & x_3\\
= &\ розрив {1} {2} & y_1 & y_2 & y_3\\
& 1 & 1\\\
\ мітка {2.2.12}\ тег {2.2.12}
\ кінець {масив}

* З моменту написання цього розділу мені стало відомо про різницю в американському/британському вживанні слова «трапеція». Мабуть, у британському вживанні «трапеція» означає чотирикутник з двома паралельними сторонами. У американському використанні трапеція означає чотирикутник без паралельних сторін, тоді як чотирикутник з двома паралельними сторонами є «трапецією». Як і у багатьох словах, у Канаді можна почути британські або американські звичаї. У вищезгаданому виведенні я мав намір британське використання. З цього слід навчитися тому, що ми завжди повинні дбати про те, щоб чітко зрозуміти себе, використовуючи такі неоднозначні слова, і не вважати, що читач буде тлумачити їх так, як ми маємо намір.

Читач може захотіти попрацювати альтернативним методом, використовуючи результати, які ми отримали раніше. Такий же результат вийде. У випадку, якщо алгебра виявиться трохи втомливою, може бути легше працювати за допомогою числового прикладу, такого як: обчислити площу трикутника\(\text{ABC}\)\(\text{A}\)\(\text{B}\), де,\(\text{C}\) - точки (2,3), (7,4), (5,6) відповідно. У другому способі відзначимо, що площа трикутника дорівнює\(\frac{1}{2} \times \text{base} \times \text{height}\). Таким чином, якщо ми можемо знайти довжину сторони BC, і перпендикулярну відстань\(\text{A}\) від\(\text{BC}\), ми можемо це зробити. Перший простий:

\[(\text{BC})^2 = (x_3 - x_2)^2 + (y_3 - y_2)^2 . \label{2.2.13} \tag{2.2.13}\]

Щоб знайти друге, ми можемо легко записати Рівняння до рядка\(\text{BC}\) з Рівняння\(\ref{2.2.3}\), а потім переписати його у формі\(\ref{2.2.7}\). Тоді Рівняння\(\ref{2.2.11}\) дозволяє нам знайти перпендикулярну відстань\(\text{A}\) від\(\text{BC}\), а решта легко.

Якщо визначник у Рівнянні\(\ref{2.2.12}\) дорівнює нулю, площа трикутника дорівнює нулю. Це означає, що три точки є колінеарними.

Кут між двома лініями

\[y = m_1 x + c_1 \label{2.2.14} \tag{2.2.14}\]

і\[ y = m_2 x + c_2 \label{2.2.15} \tag{2.2.15}\]

легко знайти, нагадавши, що кути, які вони роблять з\(x\) -віссю є\(\tan^{-1} \ m_1\) і\(\tan^{-1} \ m_2\) разом з елементарною формулою тригонометрії\(\tan( A − B) = (\tan A − \tan B) / (1+ \tan A \tan B)\). Тоді зрозуміло, що тангенс кута між двома лініями

\[\frac{m_2 - m_1}{1+ m_1 m_2} . \label{2.2.16} \tag{2.2.16}\]

Дві лінії знаходяться під прямим кутом один до одного, якщо

\[m_1 m_2 = -1 \label{2.2.17} \tag{2.2.17}\]

Лінія, яка розділяє кут між лініями, є місцем розташування точок, які знаходяться на рівній відстані від двох ліній. Для прикладу розглянемо два рядки

\[-2x + 5y = 1 \label{2.2.18} \tag{2.2.18}\]

\[30x - 10y = 1 \label{2.2.19} \tag{2.2.19}\]

Використовуючи рівняння\(\ref{2.2.11}\), ми бачимо, що точка\((x , y)\) рівновіддалена від цих двох ліній, якщо

\[\frac{1+2x-5y}{\sqrt{29}} = \pm \frac{1-30x+10y}{\sqrt{1000}}. \label{2.2.20} \tag{2.2.20}\]

Значення волі\(\pm\) стане очевидним незабаром. Результат вибору + та − відповідно у

\[-8.568x + 8.079y = 1 \label{2.2.21} \tag{2.2.21}\]

і\[2.656x + 2.817y = 1. \label{2.2.22} \tag{2.2.22}\]

Дві безперервні лінії на малюнку\(\text{II.3}\) - це лінії\(\ref{2.2.18}\) і\(\ref{2.2.19}\). Є дві бісектриси, представлені рівняннями\(\ref{2.2.21}\) і\(\ref{2.2.22}\), показані у вигляді пунктирних ліній на малюнку, і вони знаходяться під прямим кутом один до одного. Вибір знака + у Рівнянні\(\ref{2.2.20}\) (що в цьому випадку призводить до Рівняння\(\ref{2.2.21}\), бісектриса на малюнку\(\text{II.3}\) з додатним нахилом) дає бісектрису сектора, який містить початок.

Рівняння форми

\[ax^2 + 2hxy + by^2 = 0 \label{2.2.23} \tag{2.2.23}\]

може бути враховано на два лінійні фактори без постійного члена, і тому він являє собою дві лінії, що перетинаються біля початку. Залишається як вправа, щоб визначити кути, які дві лінії роблять один з одним і з\(x\) віссю, і показати, що лінії

\[x^2 + \left( \frac{a-b}{h} \right) xy - y^2 = 0 \label{2.2.24} \tag{2.2.24} \]

є бісектрисами\(\ref{2.2.23}\) і перпендикулярні один одному.

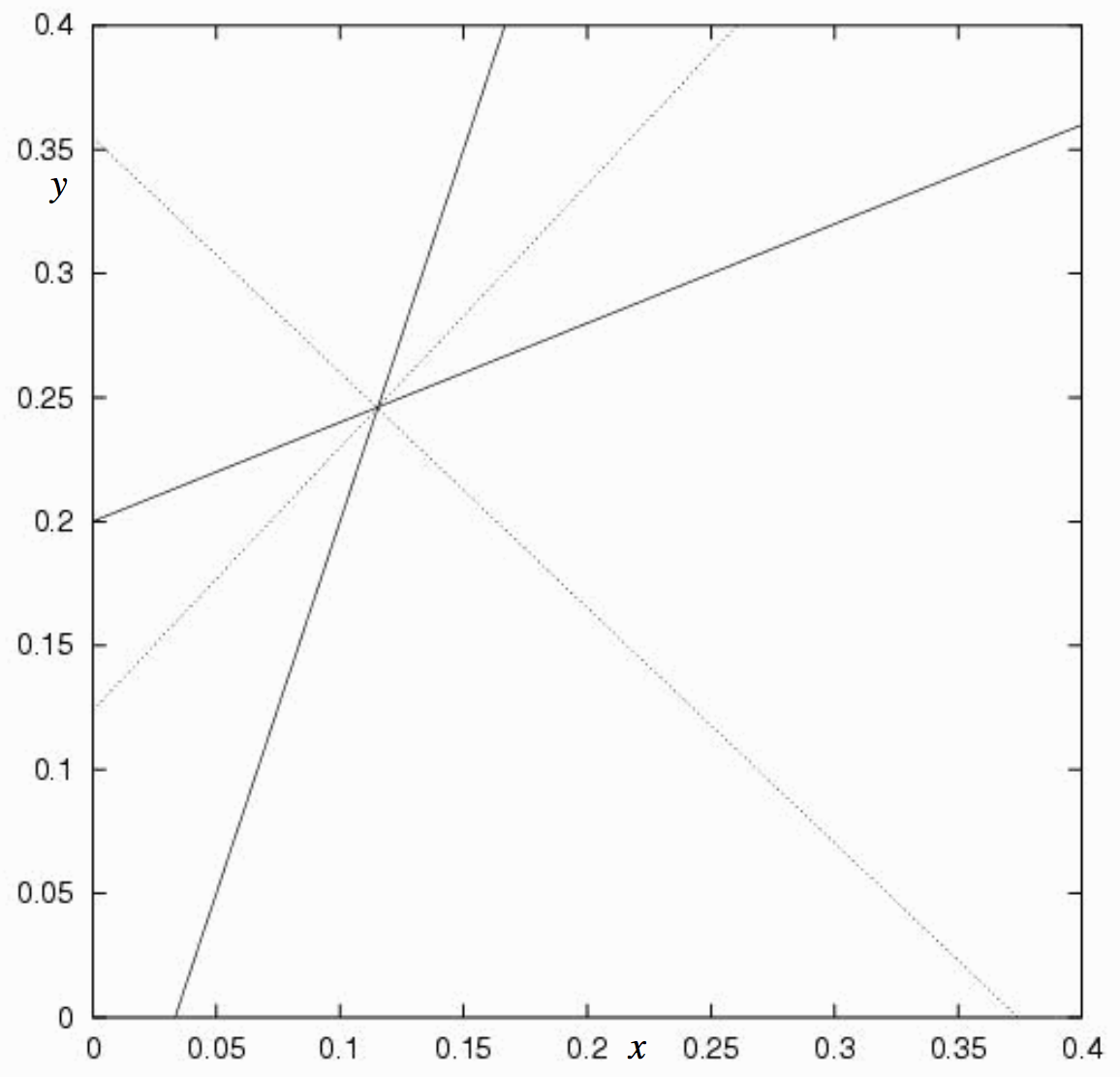
\(\text{FIGURE II.3}\)

Враховуючи рівняння до трьох прямих, чи можемо ми знайти площу трикутника, обмежену ними? Знайти загальний алгебраїчний вираз може бути трохи нудним, хоча читач може захотіти спробувати його, але числовий приклад простий. Для прикладу розглянемо лінії

\[x - 5y + 12 = 0, \label{2.2.25} \tag{2.2.25}\]

\[3x + 4y - 9 = 0, \label{2.2.26} \tag{2.2.26}\]

\[3x - y - 3 = 0. \label{2.2.27} \tag{2.2.27}\]

Розв'язуючи рівняння парами, незабаром з'ясовується, що вони перетинаються в точках (−0.15789, 2.36842), (1.4, 1.2) та (1.92857, 2.78571). Застосування Рівняння\(\ref{2.2.12}\) потім дає площу як 1,544. Трикутник малюється на малюнку\(\text{II.4}\). Виміряйте будь-яку сторону і відповідну висоту лінійкою і подивіться, чи дійсно площа близько 1,54.

Але тепер розглянемо три рядки

\[x - 5y + 12 = 0, \label{2.2.28} \tag{2.2.28}\]

\[3x + 4y - 9 = 0 , \label{2.2.29} \tag{2.2.29}\]

\[3x + 23y - 54 = 0. \label{2.2.30} \tag{2.2.30}\]

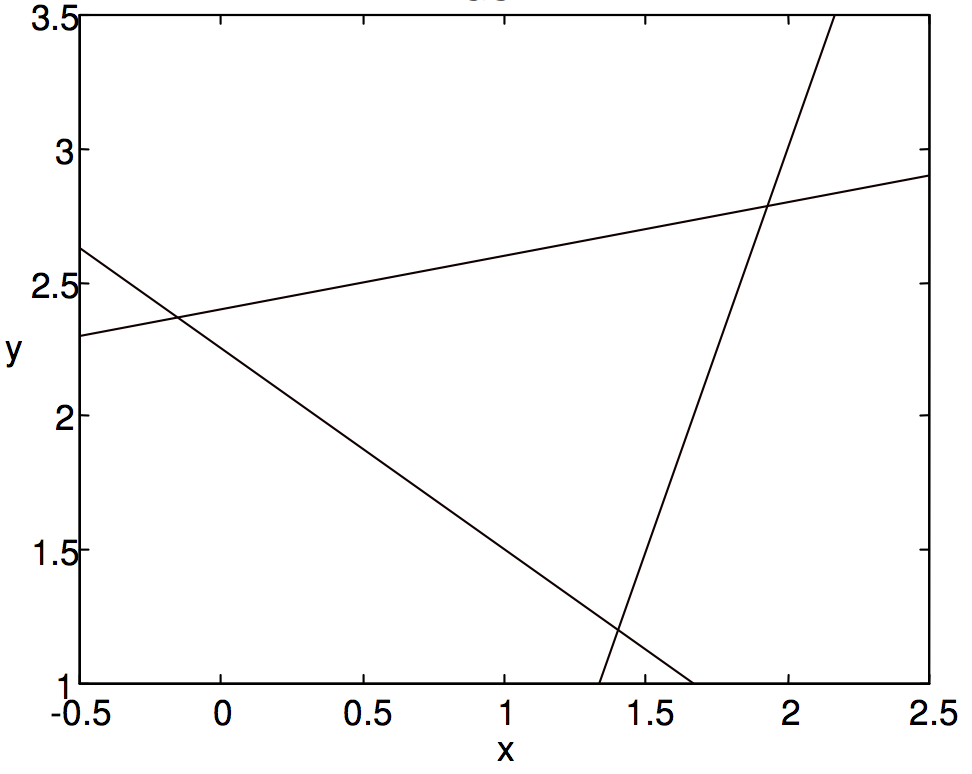
\(\text{FIGURE II.4}\)

Вирішуючи рівняння попарно, буде встановлено, що всі три лінії перетинаються в одній точці (будь ласка, зробіть це), а площа трикутника, звичайно, дорівнює нулю. Будь-яке з цих рівнянь є, по суті, лінійною комбінацією двох інших. Ви повинні намалювати ці три лінії точно на графічному папері (або за допомогою комп'ютера). Загалом, якщо три рядки

\[A_1 x + B_1 y + C_1 = 0 \label{2.2.31} \tag{2.2.31}\]

\[A_2 x + B_2y + C_2 = 0 \label{2.2.32} \tag{2.2.32}\]

\[A_3 x + B_3 y + C_3 = 0 \label{2.2.33} \tag{2.2.33}\]

вони будуть одночасними в одній точці, якщо

\ begin {масив} {| c c | c}
A_1 & B_1 & C_1\\
A_2 & B_2 & C_2 & = 0. \\
A_3 & B_3 & C_3\\
\ мітка {2.2.34}\ тег {2.2.34}
\ кінець {масив}

Таким чином, детермінант у Рівнянні\(\ref{2.2.12}\) забезпечує перевірку того, чи три точки є колінеарними, а детермінант у Рівнянні\(\ref{2.2.34}\) забезпечує перевірку того, чи три лінії є одночасними.

Нарешті - принаймні для цієї глави - може бути рідкісний привід записати Рівняння прямої в полярних координатах. З малюнка повинно бути видно\(\text{II.5}\), що рівняння

\[r = p \csc (\theta - \alpha) \ \text{or} \ r = p \csc (\alpha - \theta) \label{2.2.35} \tag{2.2.35}\]

опишіть пряму лінію, що проходить на відстані\(p\) від полюса і зробивши кут\(\alpha\) з початковою лінією. Якщо\(p = 0\), полярне рівняння є просто\(\theta = \alpha\).

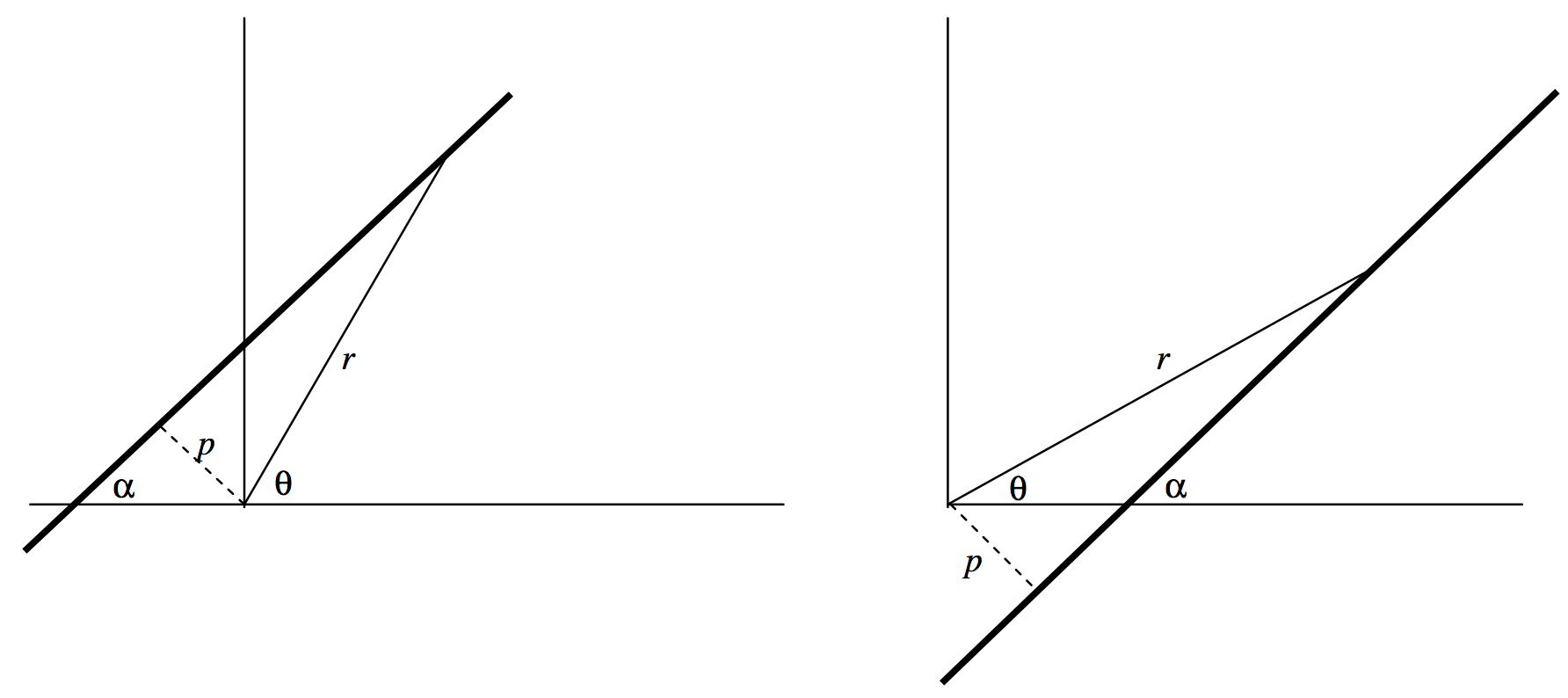
\(\text{FIGURE II.5}\)