1.10:1.10-Бесселівська інтерполяція

Last updated
Save as PDF

Page ID: 78098

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

За кілька днів до широкого використання високошвидкісних комп'ютерів широко використовувалося друковані таблиці загальних математичних функцій. Наприклад, таблиця функції Бесселя\(J_0 (x)\) вказувала б

\[J_0 (1.7) = 0.397 \ 984 \ 859 \nonumber\]

\[J_0(1.8) = 0.339 \ 986 \ 411 \nonumber\]

Якби хтось хотів функцію Бесселя\(x = 1.762\), потрібно було б інтерполювати між табличними значеннями.

Сьогодні було б простіше просто обчислити функцію Бесселя для будь-якого конкретного бажаного значення аргументу\(x\), і сьогодні менше потреби в друкованих таблицях або знати, як інтерполювати. Дійсно, більшість обчислювальних систем сьогодні мають внутрішні процедури, які дозволять обчислити простолюдні функції, такі як функції Бесселя, навіть якщо у вас є лише туманне уявлення про те, що таке функція Бесселя.

Однак потреба не зовсім минула. Наприклад, в орбітальних розрахунках нам часто потрібні геоцентричні координати Сонця. Вони не є тривіальними для обчислення неспеціалістів, і може бути простіше шукати їх в Астрономічному альманасі, де він зведений у таблиці на кожен день року, наприклад, 14 липня та 15 липня. Але, якщо потрібно\(y\) 14 липня 395, як інтерполювати?

В ідеальному світі таблична функція буде таблична через досить тонкі проміжки часу, так що лінійна інтерполяція між двома табличними значеннями була б достатньою для повернення функції до тієї ж кількості значущих цифр, що і табличні точки. Світ не досконалий, однак, і для досягнення такої досконалості інтервал табуляції повинен був би змінюватися, оскільки функція змінювалася більш-менш швидко. Отже, нам потрібно знати, як робити нелінійну інтерполяцію.

Припустимо, функція\(y(x)\)\(x = x_1\) зведена в таблицю в і\(x = x_2\), інтервал\(x_2 − x_1\) буття\(δx\). Якщо хтось бажає знайти значення\(y\) at\(x + \theta δx\), лінійна інтерполяція дає

\[y(x_1 + \theta \Delta x) = y_1 + \theta (y_2 - y_1) = \theta y_2 + (1-\theta) y_1 , \label{1.10.1} \tag{1.10.1}\]

де\(y_1 = y(x_1)\) і\(y_2 = y(x_2)\). Тут передбачається, що це дріб між\(0\) і\(1\); якщо\(\theta\) знаходиться поза цим діапазоном (що є негативним, або більше, ніж\(1\)), ми екстраполяція, а не інтерполяція, і це завжди небезпечно робити.

Давайте тепер розглянемо ситуацію, коли лінійна інтерполяція недостатньо хороша. Припустимо,\(y(x)\) що функція зведена в таблицю для чотирьох точок\(x_1, \ x_2, \ x_3, \ x_4\) аргументу\(x\), відповідні значення функції\(y_1, \ y_2, \ y_3, \ y_4\). Бажаємо оцінити\(y\) для того\(x = x_2 + \theta δx\),\(δx\) де інтервал\(x_2 - x_1\) або\(x_3 - x_2\) або\(x_4 - x_3\). Ситуація проілюстрована на малюнку\(\text{I.6A}\).

Можливим підходом було б пристосувати многочлен до чотирьох сусідніх точок:

\[y = a + bx + cx^2 + dx^3 . \]

Ми запишемо це рівняння для чотирьох сусідніх табличних точок і вирішуємо для коефіцієнтів, і, отже, ми можемо оцінити функцію для будь-якого значення\(x\), що нам подобається в інтервалі між\(x_1\) і\(x_4\). На жаль, це цілком може включати більше обчислювальних зусиль, ніж оцінка самої оригінальної функції.

альт
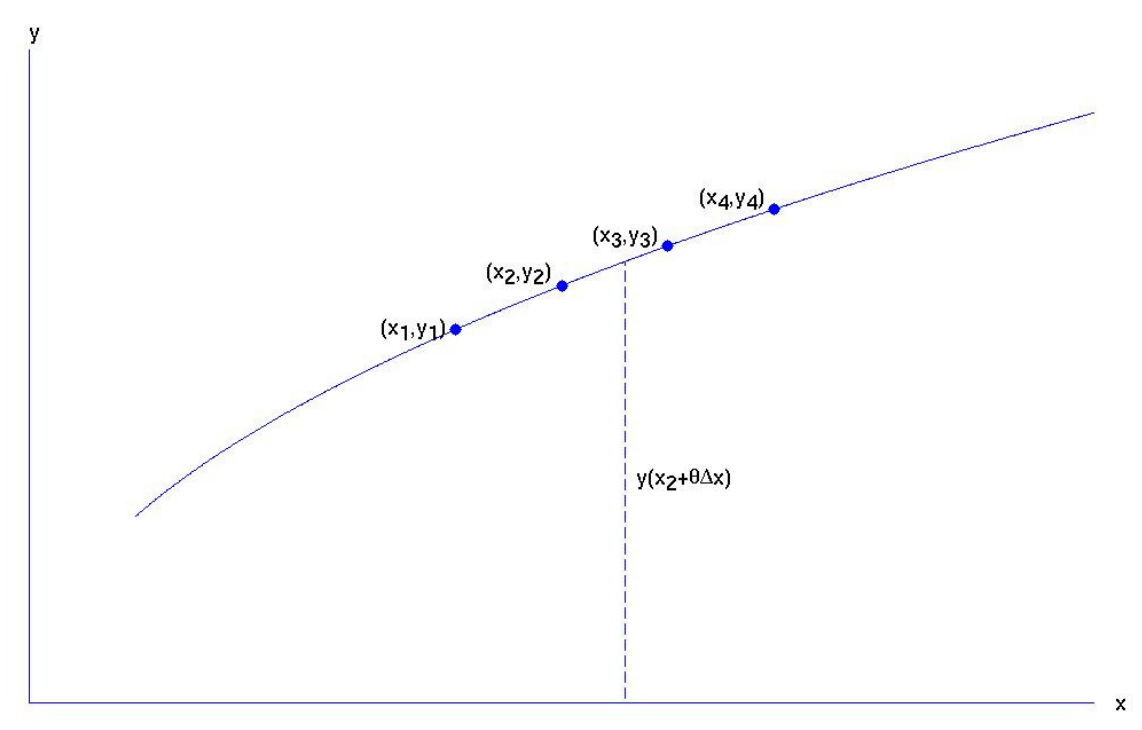
\(\text{FIGURE I.6A}\)

Задача була вирішена зручним чином з точки зору скінченно-різницевого числення, логічний розвиток якого передбачав би додаткову істотну главу, що виходить за рамки передбачуваної книги. Тому я просто надаю метод лише, без доказів.

Суть методу полягає в тому, щоб скласти таблицю відмінностей, як показано нижче. Перші дві колонки -\(x\) і\(y\). Записи в інших стовпцях - це відмінності між двома записами в стовпці відразу ліворуч. Таким чином, наприклад,\(δ_{4.5} = y_5 - y_4\)\(δ_4^2 = δ_{4.5} - δ_{3.5}\), і т.д.

альт

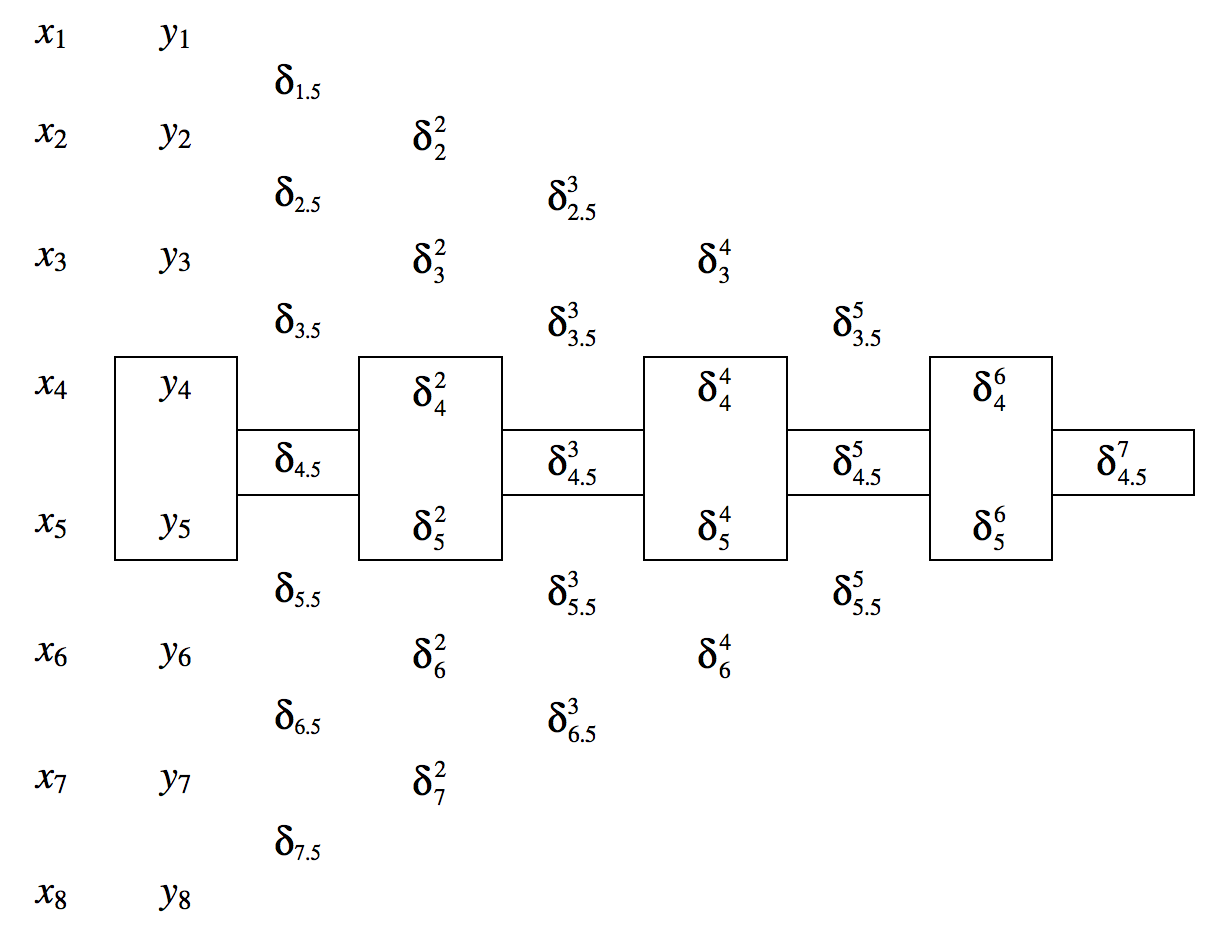
Давайте припустимо, що ми хочемо знайти\(y\) для значення\(x\), що є\(\theta\) часткою шляху від\(x_4\) до\(x_5\). Формула інтерполяції Бесселя

\[y(x) = \frac{1}{2} (y_4 + y_5) + B_1 δ_{4.5} + B_2 ( δ_4^2 + δ_5^2) + B_3 δ_{4.5}^3 + B_4 (δ_4^4 + δ_5^4) + ... \label{1.10.3} \tag{1.10.3}\]

Тут\(B_n\) наведені коефіцієнти інтерполяції Бесселя, а послідовні члени в дужках у розширенні - це суми чисел у графах таблиці.

Коефіцієнти Бесселя

\[B_n (\theta) = \frac{1}{2} \begin{pmatrix} \theta + \frac{1}{2}n - 1 \\ n \end{pmatrix} \quad \text{if n is even,} \label{1.10.4} \tag{1.10.4}\]

і\[B_n (\theta) = \frac{\theta - \frac{1}{2}}{n} \begin{pmatrix} \theta + \frac{1}{2}n - \frac{3}{2} \\ n-1 \end{pmatrix} \quad \text{if n is odd.} \label{1.10.5} \tag{1.10.5}\]

Позначення\(\begin{pmatrix} m \\ n \end{pmatrix}\) означає коефіцієнт х м в біноміальному розширенні\((1 + x)^n\).

Явно,

\[B_1 = \theta - \frac{1}{2} \label{1.10.6} \tag{1.10.6}\]

\[B_2 = \frac{1}{2} \theta ( \theta - 1 ) / 2! = \theta (\theta - 1) / 4 \label{1.10.7} \tag{1.10.7}\]

\[B_3 = (\theta - \frac{1}{2}) \theta ( \theta - 1) / 3! = \theta (0.5 + \theta (-1.5 + \theta ))/6 \label{1.10.8} \tag{1.10.8}\]

\[B_4 = \frac{1}{2} ( \theta + 1) \theta ( \theta - 1) ( \theta - 2) / 4 ! = \theta ( 2 + \theta ( -1 + \theta ( -2 + \theta ))) / 48 \label{1.10.0} \tag{1.10.9}\]

\[B_5 = (\theta - \frac{1}{2} ) ( \theta + 1) \theta ( \theta - 1) (\theta - 2) / 5 ! = \theta ( -1 + \theta ( 2.5 + \theta^2 (-2.5 + \theta )))/120 \label{1.10.10} \tag{1.10.10}\]

Читач повинен переконати його або себе, що формула інтерполяції, прийнята настільки, наскільки\(B_1\) це просто лінійна інтерполяція. Додавання послідовно вищих термінів ефективно підходить до кривої до все більшої кількості точок навколо бажаного значення і все більш точно відображає фактичну зміну\(y\) з\(x\).

альт

Наведена вище таблиця взята з Астрономічного альманаху за 1997 рік, і вона показує\(y\) координату Сонця протягом восьми днів поспіль у липні. Перші три стовпці відмінностей зведені в таблицю, і зрозуміло, що подальші стовпці відмінностей є необґрунтованими.

Якщо ми хочемо знайти значення\(y\), наприклад, для липня 4.746, ми маємо\(\theta = 0.746\) і перші три коефіцієнти Бесселя

\ begin {масив} {c c l}
B_1 & = & +0.246\\
B_2 & = & -0.047\ 371\
B_3 & = & -0.007\ 768\ 844\
\ nonumber
\ end {масив}

Читач може перевірити наступні\(y\) розрахунки за сумою перших 2, 3 і 4 членів Бесселівської інтерполяційної серії формули. Сума перших двох членів є результатом лінійної інтерполяції.

Сума перших 2-х членів,\(y = 0.909 \ 580 \ 299\)
Сума перших 3 членів,\(y = 0.909 \ 604 \ 723\)
Сума перших 4-х членів,\(y = 0.909 \ 604 \ 715\)

За умови, що таблиця не зведена в таблицю з невідповідними грубими інтервалами, потрібно рідко йти повз третього коефіцієнта Бесселя. У цьому випадку альтернативною та еквівалентною формулою інтерполяції (для\(t = t_4 + \theta \Delta t)\), яка дозволяє уникнути необхідності побудови таблиці різниць, є

\ begin {масив} {c c l}
y (t_4 +\ тета\ дельта t) & = & -\ frac {1} {6}\ тета [(2 -\ тета (3-\ тета)) y_3 + (1 -\ тета) y_6]\\
& & +\ frac {1} {2} [(2 +\ тета (-1 +\ тета (-2 +\ тета (-2)))) y_4 +\ тета (2 +\ тета (1 -\ тета)) y_5].
\ end {масив}

Читачі повинні перевірити, що це дає однакову відповідь, при цьому зазначивши, що вкладені дужки роблять розрахунок дуже швидким і їх легко запрограмувати або на калькуляторі, або на комп'ютері.

Вправа\(\PageIndex{1}\): Bessel Coefficients

З наведеної нижче таблиці побудуйте таблицю різниць до четвертих відмінностей. Обчисліть перші чотири коефіцієнти Бесселя для\(\theta = 0.73\). Звідси обчислити значення\(y\) for\(x = 0.273\).

\ begin {масив} {c c}
x & y\\
0.0 & + 0.381300\\
0.1 & + 0.285603\\
0.2 & + 0.190 092\\
0.3 & + 0,096327\\
0.4 & + 0,008 268\\
0.5 & - 0.067 725\\
\ кінець {масив}

Відповіді

\(B_1 = +0.23\)
\(B_2 - - 0.049275\)
\(B_3 = -7.5555 \times 10^{-3}\)
\(B_4 = +9.021841875 \times 10^{-3}\)
\(y = 0.121289738\)

Примітка: таблиця розраховувалася за формулою, а інтерпольована відповідь правильна до дев'яти значущих цифр.

Вправа\(\PageIndex{2}\): Linear Interpolation vs. Besselian Interpolation

З наведеної нижче таблиці використовуйте лінійну інтерполяцію та бесселівську інтерполяцію\(\sin 51^\circ\) для оцінки трьох значущих цифр.\(\sin x\)

\ begin {масив} {c c}
x^\ circ &\ sin х\
\\\
0 & 0.0\\
30 & 0.5\\
60 &\ sqrt {3} /2 - 0.86603\\
90 & 1.0\
\ end {масив}

Відповіді

За допомогою лінійної інтерполяції\(\sin 51^\circ = 0.634.\)
За бесселівської інтерполяцією,\(\sin 51^\circ = 0.776.\)

Правильне значення - 0,777. Ви повинні бути вражені - але в розділі 1.11 буде більше інтерполяції.