1.9: Нелінійні синхронні рівняння

Розглянуто два одночасних рівняння виду

$$f(x, \ y) = 0, \label{1.9.1}$$

$$g(x, \ y) = 0 \label{1.9.2}$$

в яких Рівняння не є лінійними.

Як приклад розв'яжемо Рівняння

$$x^2 = \frac{a}{b-\cos y} \label{1.9.3}$$

$$x^3 - x^2 = \frac{a(y-\sin y \cos y)}{\sin^3 y} , \label{1.9.4}$$

в яких$a$ і$b$ є константами, значення яких приймаються заданими в якомусь конкретному випадку.

Це може здатися штучно надуманою парою рівнянь, але насправді пара рівнянь, як це, з'являється в орбітальної теорії.

Ми пропонуємо тут два методи розв'язання рівнянь.

У першому ми зауважимо, що насправді$x$ можна виключити з двох рівнянь, щоб отримати одне рівняння в$y$:

$$F(y) = aR^3 - R^2 - 2SR - S^2 = 0, \label{1.9.5}$$

де $$R = 1/(b-\cos y) \label{1.9.5a} \tag{1.9.5a}$$

і $$S = (y - \sin y \cos y ) / \sin^3 y . \label{1.9.5b} \tag{1.9.5b}$$

Вирішити це можна звичайним методом Ньютона-Рафсона, який є багаторазовим застосуванням$y = y − F / F^\prime$. Похідне по відношенню$y$ до$F$

$$F^\prime = 3aR^2 R^\prime - 2RR^\prime - 2(S^\prime R + SR^\prime) - 2SS^\prime \label{1.9.6}$$

де $$R^\prime = -\frac{\sin y}{(b-\cos y)^2} \label{1.9.6a} \tag{1.9.6a}$$

і $$S^\prime = \frac{\sin y (1 - \cos 2y ) - 3\cos y (y- \frac{1}{2} \sin 2y)}{\sin^4 y} \label{1.9.6b} \tag{1.9.6b}$$

Незважаючи на те, що може здатися на перший погляд деякими досить складними рівняннями, буде встановлено, що процес Ньютона-Рафсона$y = y − F / F^\prime$, досить простий в програмуванні, хоча, для обчислювальних цілей,$F$ і$F^\prime$ краще написані як

$$F = -S^2 + R(-2S + R (-1 + aR)) , \label{1.9.7a} \tag{1.9.7a}$$

і

$$F^\prime = 3aR^2 R^\prime - 2(R+S)(R^\prime + S^\prime ) \label{1.9.7b} \tag{1.9.7b}$$

Давайте розглянемо конкретний приклад, скажімо з$a = 36$ і$b = 4$. Треба, звичайно, зробити перше припущення. У орбітальному додатку, описаному в главі 13, пропонуємо перше припущення. У даному випадку, з$a = 36$ і$b = 4$, одним із способів було б побудувати графіки рівнянь$\ref{1.9.3}$$\ref{1.9.4}$ і подивитися, де вони перетинаються. Ми зробили це на малюнку 1.4, з якого ми бачимо, що y повинен бути близьким до$0.6$.

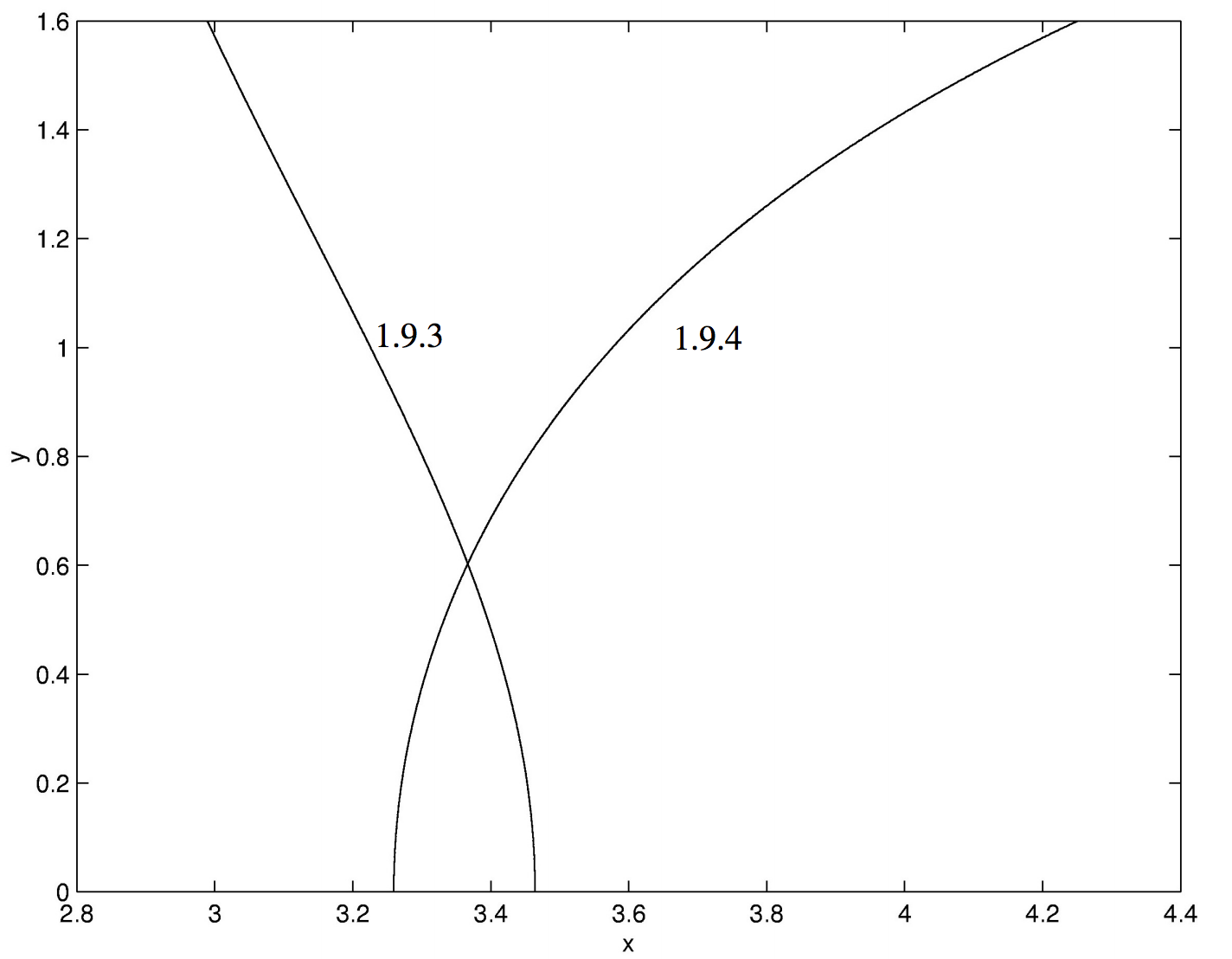
$\text{FIGURE 1.4}$
Рівняння$\ref{1.9.3}$ і$\ref{1.9.4}$ з$a=36$ і$b=4$.

З першим припущенням$y = 0.6$, збіжність до$y = 0.60292$ досягається в двох ітераціях, і будь-який з двох оригінальних рівнянь потім дає$x = 3.3666$.

Нам пощастило в цьому випадку в тому, що ми виявили, що ми змогли усунути одну зі змінних і так звести задачу до єдиного рівняння на одному невідомому. Однак будуть випадки, коли усунення одного з невідомих може бути значно складнішим або, у випадку двох одночасних трансцендентних рівнянь, неможливим алгебраїчними засобами. Наступний ітераційний метод, розширення техніки Ньютона-Рафсона, майже завжди може бути використаний. Ми описуємо його для двох рівнянь у двох невідомих, але його можна легко розширити до$n$ рівнянь у$n$ невідомих.

Рівняння, що підлягають розв'язанню

$$f(x, \ y) = 0 \label{1.9.8} \tag{1.9.8}$$

$$g(x, \ y) = 0 . \label{1.9.9} \tag{1.9.9}$$

Як і при розв'язанні одного рівняння, спочатку необхідно здогадатися про розв'язки. У деяких випадках це може бути зроблено графічними методами. Однак дуже часто, як це часто зустрічається з методом Ньютона-Рафсона, конвергенція відбувається стрімко навіть тоді, коли перше припущення дуже неправильне.

Припустимо, початкові здогадки є$x + h$$y + k$, де$x$,$y$ є правильними рішеннями,$h$ і$k$ є помилками нашого припущення. З розширення Тейлора першого порядку (або зі здорового глузду, якщо розширення Тейлора забуте),

$$f(x+h, y+k) \approx f(x,y) + hf_x + kf_y . \label{1.9.10} \tag{1.9.10}$$

Ось$f_x$ і$f_y$ часткові похідні і звичайно$f(x, \ y) = 0$. Ті самі міркування стосуються другого рівняння, тому ми приходимо до двох лінійних рівнянь у$h$ помилках$k$:

$$f_x h + f_y k = f , \label{1.9.11} \tag{1.9.11}$$

$$g_x h + g_y k = g. \label{1.9.12} \tag{1.9.12}$$

Вони можуть бути вирішені для$h$ і$k$:

$$h = \frac{g_y f - f_y g}{f_x g_y = f_y g_x}, \label{1.9.13} \tag{1.9.13}$$

$$k = \frac{f_x g - g_x f}{f_x g_y - f_y g_x}. \label{1.9.14} \tag{1.9.14}$$

Ці значення$h$ і потім$k$ віднімаються з першого припущення, щоб отримати кращу здогадку. Процес повторюється до тих пір, поки зміни$x$ не$y$ будуть настільки малі, як потрібно для конкретного додатка. Легко налаштувати комп'ютерну програму для вирішення будь-яких двох рівнянь; все, що зміниться від однієї пари рівнянь до іншої, - це визначення функцій$f$$g$ та їх часткових похідних.

У випадку з нашим прикладом ми маємо

$$f = x^2 - \frac{a}{b-\cos y} \label{1.9.15} \tag{1.9.15}$$

$$g = x^3 - x^2 - \frac{a(y-\sin y \cos y)}{\sin^3 y} \label{1.9.16} \tag{1.9.16}$$

$$f_x = 2x \tag{1.9.17} \label{1.9.17}$$

$$f_y = \frac{a\sin y}{(b- \cos y)^2} \label{1.9.18} \tag{1.9.18}$$

$$g_x = x(3x-2) \label{1.9.19} \tag{1.9.19}$$

$$g_y = \frac{a[3(y-\sin y \cos y) \cos y - 2\sin^3 y]}{\sin^4 y} \label{1.9.20} \tag{1.9.20}$$

У конкретному випадку де$a = 36$ і$b = 4$, ми можемо почати з першого припущення (з графіка - рис. I.4)$y = 0.6$ і звідси$x = 3.3$. Конвергенція до однієї частини в мільйон досягається за три ітерації, рішення є$x = 3.3666$,$y = 0.60292$.

Просте застосування цих міркувань виникає, якщо вам доведеться вирішити поліноміальне рівняння$f(z) = 0$, де немає реальних коренів, і всі рішення для$z$ є складними. Потім ви просто записуєте$z = x + iy$ і підставляєте це в поліноміальне рівняння. Потім зрівняйте дійсну і уявну частини окремо, щоб отримати два Рівняння виду

$$R(x, \ y ) = 0 \label{1.9.21} \tag{1.9.21}$$

$$I(x, \ y ) = 0 \label{1.9.22} \tag{1.9.22}$$

і розв'яжіть їх для x і y. наприклад, знайдіть коріння Рівняння

$$z^4 - 5z + 6 = 0 . \label{1.9.23} \tag{1.9.23}$$

Незабаром буде виявлено, що нам доведеться вирішити

$$R(x, \ y) = x^4 - 6x^2 y^2 + y^4 - 5x + 6 = 0 \label{1.9.24} \tag{1.9.24}$$

$$I(x, \ y) = 4x^3 - 4xy^2 - 5 = 0 \label{1.9.25} \tag{1.9.25}$$

Було помічено, що для отримання останнього рівняння ми розділили через$y$, що допустимо, оскільки ми знаємо$z$, що є складними. Ми також зауважимо, що$y$ тепер відбувається тільки як$y^2$, так це спростить речі, якщо ми дозволимо$y^2 = Y$, а потім вирішити Рівняння

$$f(x, Y) = x^4 - 6x^2 Y + Y^2 - 5x + 6 = 0 \label{1.9.26} \tag{1.9.26}$$

$$g(x,Y) = 4x^3 - 4xY - 5 = 0 \label{1.9.27} \tag{1.9.27}$$

Потім легко вирішити будь-яку з них$Y$ як функцію$x$ і, отже, графік двох функцій (рисунок$\text{I.5}$):

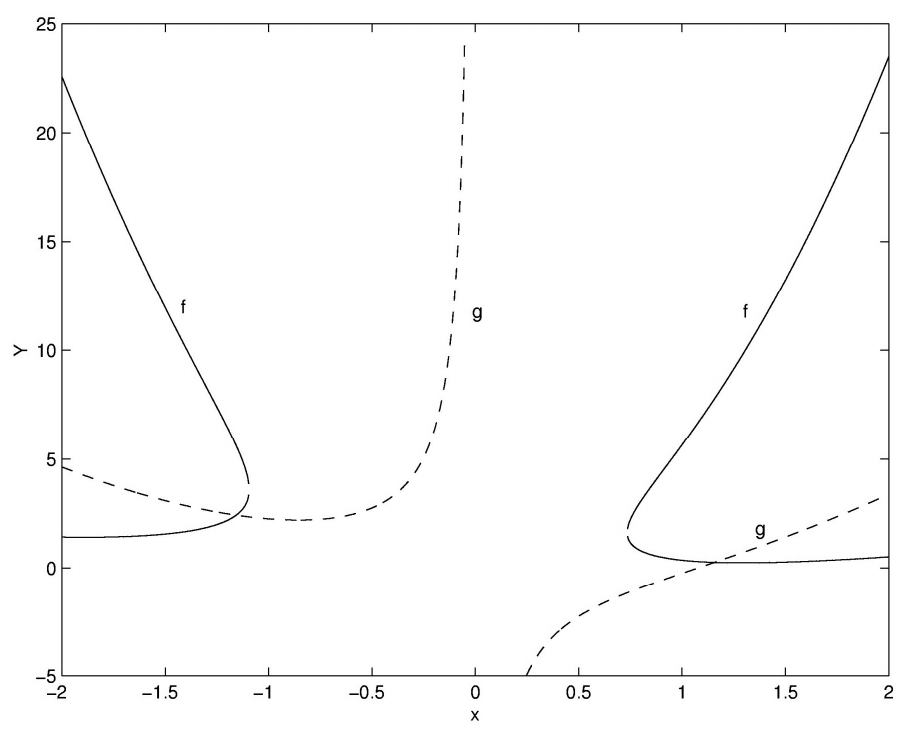
$\text{FIGURE I.5}$

Це дозволяє нам зробити перше припущення щодо рішень, а саме

$$x = -1.2, \quad Y = 2.4 \nonumber$$

і $$x= +1.2, \quad Y = 0.25818 \nonumber$$

Потім ми можемо вдосконалити рішення за допомогою розширеної техніки Ньютона-Рафсона для отримання

$$x = -1.15697, \quad Y = 2.41899 \nonumber$$

$$x = +1.15697, \quad Y = 0.25818 \nonumber$$

тому чотири рішення оригінального рівняння

$$z = -1.15697 \pm 1.55531i \nonumber$$

$$z = 1.15697 \pm 0.50812i \nonumber$$