1.2: Чисельна інтеграція

Є багато випадків, коли можна побажати інтегрувати вираз чисельно, а не аналітично. Іноді не вдається знайти аналітичний вираз для інтеграла, або, якщо можна, він настільки складний, що так само швидко інтегрується чисельно, як і таблиця аналітичного виразу. Або один може мати таблицю чисел для інтеграції, а не аналітичне рівняння. Багато комп'ютерів та програмованих калькуляторів мають внутрішні процедури інтеграції, які можна закликати (під загрозою), не маючи уявлення про те, як вони працюють. Передбачається, що читач цієї глави, однак, хоче мати можливість здійснити числове інтегрування, не закликаючи існуючу рутину, написану кимось іншим.

Існує багато різних методів числового інтегрування, але той, який відомий як Правило Сімпсона, легко програмується, швидкий у виконанні і, як правило, дуже точний. (Томас Сімпсон, 1710 - 1761, був англійським математиком, автором Нового трактату про флюксиони.)

Припустимо, у нас є функція\(y(x)\), яку ми хочемо інтегрувати між двома межами. Ми обчислюємо значення функції на двох межах і на півдорозі між ними, так що тепер ми знаємо три точки на кривій. Потім ми вписуємо параболу до цих трьох точок і знаходимо область під цим.

На малюнку\(y(x)\) - це функція\(\text{I.1}\), яку ми хочемо інтегрувати між межами\(x_2 − δx\) і\(x_2 + δx\). Іншими словами, ми хочемо обчислити площу під кривою. \(y_1\),\(y_2\) і\(y_3\) є значеннями

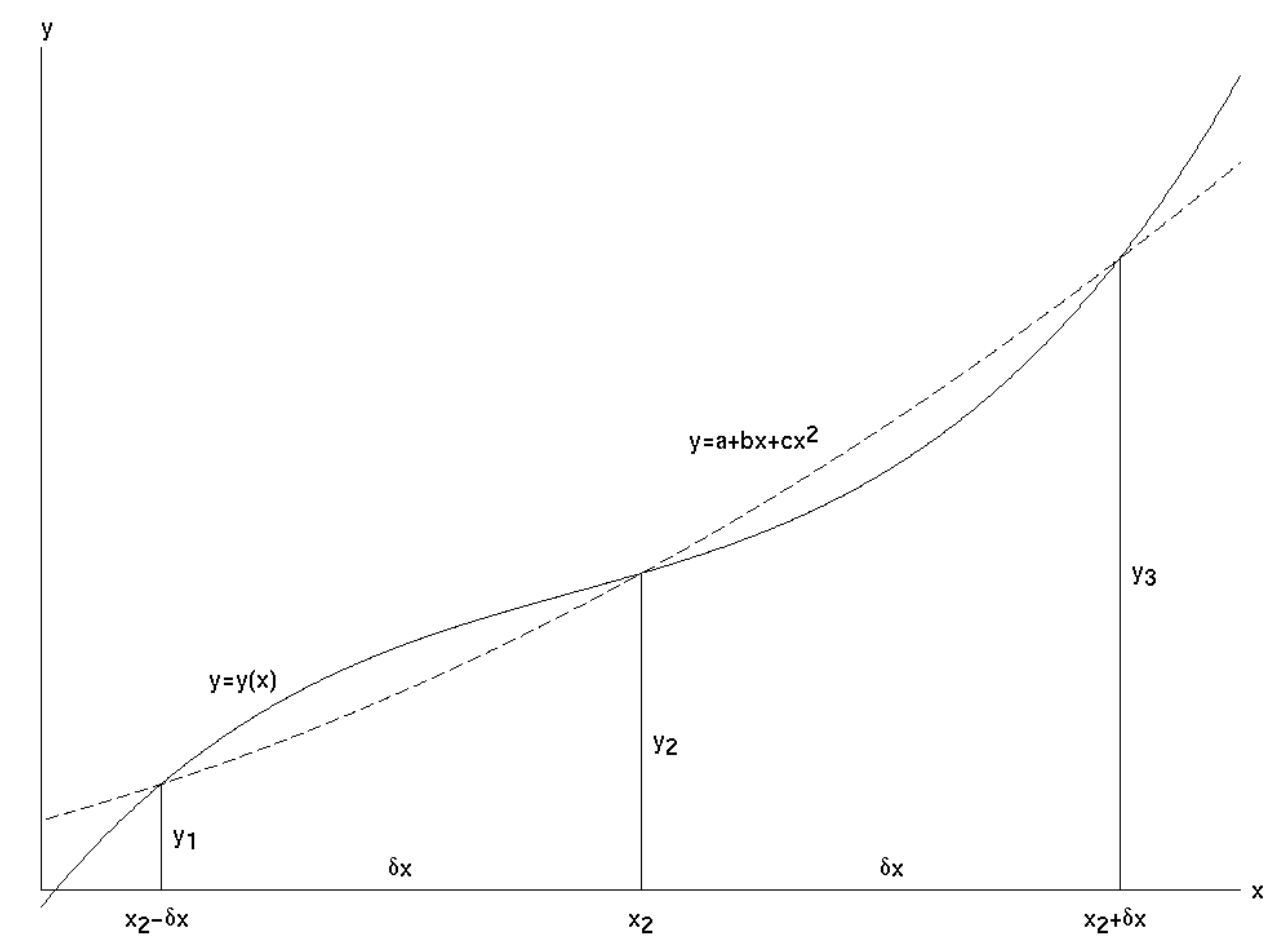
\(\text{FIGURE I.1}\)Правило Сімпсона дає нам область під параболою (пунктирною кривою), яка проходить через три точки на кривій\(y =y(x)\). Це приблизно дорівнює площі під\(y = y(x)\).

функція в\(x_2 - δ_x, \ x_2\) і\(x_2 + δ_x\), і\(y = a + bx + cx^2\) є параболою, що проходить через точки\((x_2 - δx, y_1)\),\((x_2, y_2)\) і\((x_2 + δx, y_3)\).

Якщо парабола повинна пройти через ці три точки, ми повинні мати

\[y_1 = a + b(x_2 - δx) + c(x_2 - δx)^2 \label{1.2.1}\]

\[y_2 = a + bx + cx^2 \label{1.2.2}\]

\[y_3 = a + b(x_2 + δx) + c(x_2 + δx)^2 \label{1.2.3}\]

Ми можемо вирішити ці рівняння, щоб знайти значення\(a\),\(b\) і\(c\). Це

\[a=y_2 - \frac{x_2(y_3-y_1)}{2δx} + \frac{x_2^2 (y_3 - 2y_2 + y_1)}{2(δx)^2} \label{1.2.4}\]

\[b = \frac{y_3 - y_1}{2δx} - \frac{x_2 (y_3 - 2y_2 + y_1)}{(δx)^2} \label{1.2.5}\]

\[c = \frac{y_3 - 2y_2 + y_1}{2(δx)^2} \label{1.2.6}\]

Тепер площа під параболою (яка приймається приблизно площею під\(y(x)\))

\[\int_{x_2-δx}^{x_2+δx} \left( a+bx + cx^2 \right) dx = 2 \left[ a+bx_2 + cx_2^2 + \frac{1}{3} c (δx)^2 \right] δx \label{1.2.7}\]

Про підстановку значень\(a\),\(b\) і\(c\), отримаємо для площі під параболою

\[\frac{1}{3} (y_1 + 4y_2 + y_3 ) δx \label{1.2.8}\]

і це формула, відома як Правило Сімпсона.

Для прикладу оцінимо\(\int_0^{\pi/2} \sin xdx\).

Ми будемо оцінювати функцію на нижній і верхній межі і на півдорозі між ними. Таким чином

\ begin {масив} {l l}
x= 0, & y=0\\
x =\ pi/4, & y=1/\ sqrt {2}\\
x =\ pi/2, & y=1\\
\ nonumber
\ end {масив}

Інтервал між послідовними значеннями\(x\) is\(δx = \pi/4\).

Звідси Правило Сімпсона дає область.

\[\frac{1}{3} \left( 0 + \frac{4}{\sqrt{2}}+ 1 \right) \frac{\pi}{4}\nonumber \]

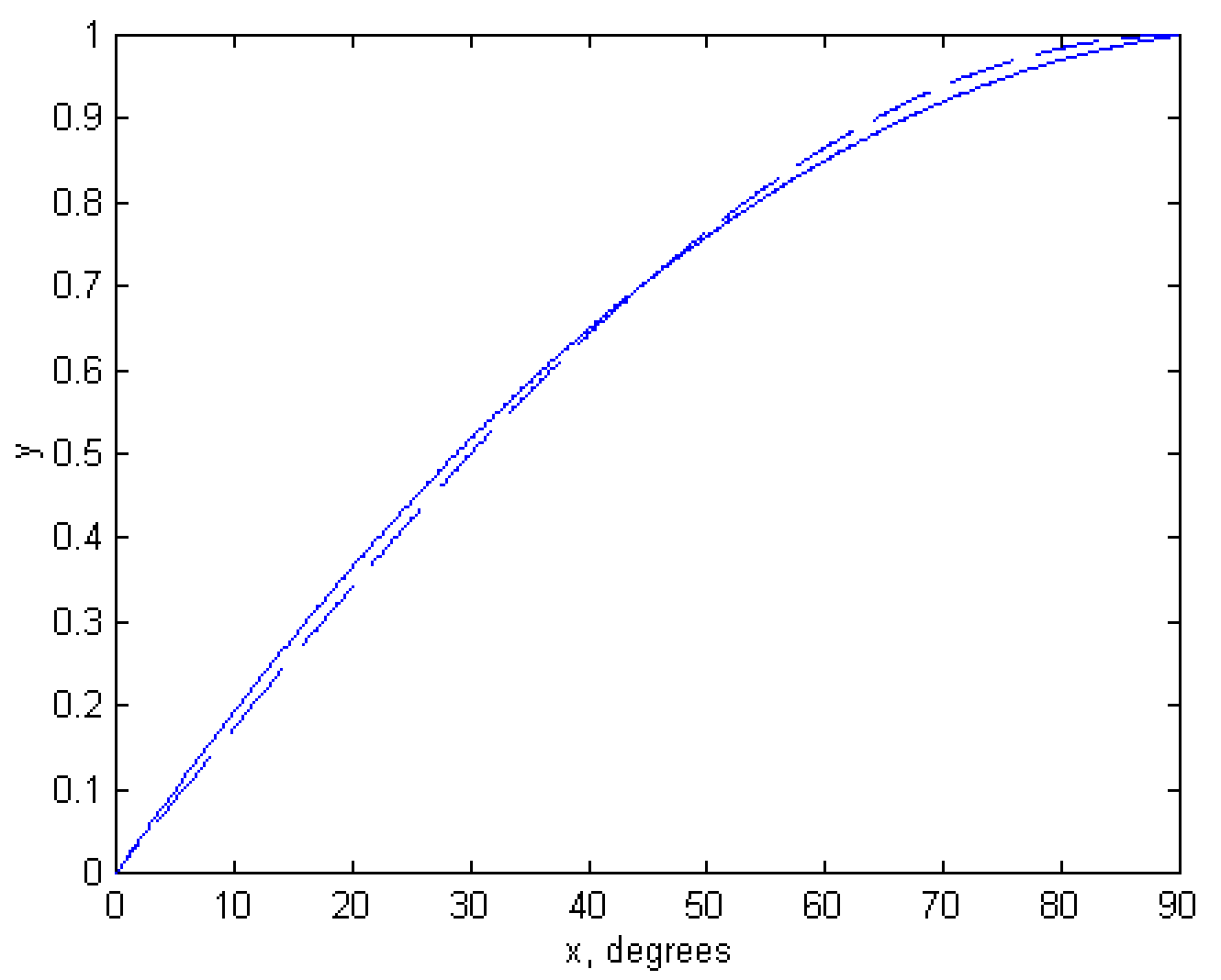
який, до трьох значущих цифр, є\(1.00\). Графіки\(\sin x\) і\(a + bx + cx^2\) наведені на малюнку\(\text{I.2a}\). Значення\(a\),\(b\) і\(c\), отримані з наведених вище формул, є

\[a=0, \quad b = \frac{\sqrt{32}-2}{\pi}, \quad c = \frac{8-\sqrt{128}}{\pi^2} \nonumber\]

\(\text{FIGURE I.2a}\)

Результат, який ми щойно отримали, досить вражаючий, і нам не завжди так щастить. Не всі функції можуть бути наближені так добре параболою. Але звичайно інтервал\(δx = \pi/4\) був смішно грубим. На практиці поділяємо інтервал на численні дуже малі інтервали. Наприклад, розглянемо інтеграл

\[\int_0^{\pi/4} \cos^{\frac{3}{2}} 2x \sin x\,dx .\nonumber\]

Розділимо інтервал\(0\)\(\pi/4\) на десять інтервалів ширини\(\pi /40\) кожен. Ми оцінимо функцію в кінцевих точках і дев'ять точок між ними, таким чином:

\ почати {масив} {c c}
х &\ cos^ {\ розрив {3} {2}} х\ sin xdx\\
0 & y_1 = 0,000\ 000\ 000\
\ pi/40 & y_2 = 0,077\ 014\ 622\\
pi/40 & y_3 = 0,145\ 091\ 486\
3\ pi/40 & y_3 4 = 0,196\ 339\ 002\\
4\ пі/ 40 & y_5 = 0,224\ 863\ 430\\
5\ пі/40 & y_6 = 0,227\ 544\ 930\\
6\ пі/40 & y_7 = 0,204\ 585\ 473\\
7\ пі/40 & y_8 = 0,159\ 828\ 877\\
8\ пі/40 & y_9 = 0.100\ 969\ 971\
9\ пі/40 & y_ {10} = 0,040\ 183 \ 066\\
10\ pi/40 & y_ {11} = 0.000\ 000\ 000\
\ nonumber
\ end {масив}

Інтеграл від\(0\) до\(2\pi /40\) є\(\frac{1}{3} (y_1 + 4y_2 + y_3) δx, \ δx\) інтервалом\(\pi/40\). Інтеграл від\(3\pi/40\) до\(4\pi/40\) є\(\frac{1}{3} ( y_3 +4y_4 +y_5 ) δx\). І так далі, поки ми не досягнемо інтеграла від\(8\pi/40\) до\(10\pi/40\). Коли ми складаємо всі ці вгору, ми отримуємо для інтеграла від\(0\) до\(\pi /4\),

\[\frac{1}{3} \left( y_1 + 4y_2 + 2y_3 + 4y_4 + 2y_5 + ... ... + 4y_{10} + y_{11} \right) δx \nonumber\]

\[=\frac{1}{3} [ y_1 + y_{11} + (y_2 + y_4 + y_6 + y_8 + y_{10} ) + 2(y_3 + y_5 + y_7 + y_9 ) ] δx, \nonumber\]

який доходить до\(0.108 \ 768 \ 816\).

Ми бачимо, що розрахунок досить швидкий, і він легко програмується (спробуйте!). Але наскільки хороша відповідь? Чи добре три значущі цифри? Чотири? П'ять?

Оскільки запрограмувати процедуру для комп'ютера досить легко, моя практика полягає в тому, щоб поділити інтервал послідовно на\(10\),\(100\),\(1000\) підінтервали, і подивитися, чи сходиться результат. У цьому прикладі, з\(N\) підінтервалами, я знайшов такі результати:

\ почати {масив} {r c}
N &\ текст {інтеграл}\
\
10 & 0.108\ 768\ 816\
100\ 709\ 621\
1000 & 0.108\ 709\ 709\ 709\ 709\ 466\\
10000 & 0.108\ 709\ 465\
\ nonномер
\ кінець { масив}

Це показує, що навіть при поділі курсу на десять інтервалів виходить досить непоганий результат, але працювати на більш значущі цифри все ж доведеться. Я використовував комп'ютер мейнфреймів, коли я робив розрахунок з\(10000\) інтервалами, і відповідь відображалася на моєму екрані в тому, що я б оцінив приблизно одну п'яту частку секунди.

Є ще два уроки, які слід витягти з цього прикладу. Один полягає в тому, що іноді зміна змінної зробить речі набагато швидше. Наприклад, якщо хтось робить один з (досить очевидних?) пробні заміни\(y = \cos x\),\(y = \cos 2x\) або\(y^2 = \cos 2x\), інтеграл стає

\[ \int_{1/\sqrt{2}}^1 (2y^2 - 1 )^{3/2} dy, \quad \int_0^1 \sqrt{\frac{y^3}{8(1+y)}} dy \quad \text{or} \quad \int_0^1 \frac{y^4}{\sqrt{2(1+y^2)}}dy. \nonumber\]

Мало того, що це дуже набагато швидше, щоб обчислити будь-який з цих integrands, ніж оригінальний тригонометричний вираз, але я знайшов відповідь\(0.108 \ 709 \ 465\) за правилом Сімпсона на третьому з них лише з\(100\) інтервалами\(10,000\), а не, відповідь з'являється на екрані, мабуть, миттєво. (Перші два вимагали ще кілька інтервалів.)

Щоб отримати приблизно одну п'яту частину секунди, може здатися невеликим моментом, але насправді обчислення пішли швидше в кілька сотень разів. Іноді чується про дуже великі обчислення, що включають величезні обсяги даних, що вимагають протягом ночі комп'ютер працює вісім годин або близько того. Якби швидкість і ефективність програмування можна було б збільшити в кілька сотень разів, як у цьому прикладі, все обчислення можна було б завершити менш ніж за хвилину.

Інший урок, який слід засвоїти, полягає в тому, що інтеграл робить, врешті-решт, мають явну алгебраїчну форму. Ви повинні спробувати знайти його не тільки для інтеграційної практики, але і переконати себе, що дійсно бувають випадки, коли числове рішення можна знайти швидше, ніж аналітичне! Відповідь, до речі, така\(\frac{\sqrt{18}\ln(1+\sqrt{2}) - 2}{16}.\)

Тепер ви можете виконати наступну інтеграцію чисельно, або вручну калькулятором або комп'ютером.

\[\int_0^2 \frac{x^2 dx}{\sqrt{2-x}} \nonumber\]

На перший погляд це може виглядати як просто чергова рутинна вправа, але ви дуже скоро знайдете невелику складність і задумаєтеся, що з цим робити. Складність полягає в тому, що на верхній межі інтеграції integrand стає нескінченним. Такого роду труднощі, які не рідко, часто можна подолати за допомогою зміни змінної. Наприклад, нехай\(x = 2 \sin^2 \theta\), і інтеграл стає

\[ 8 \sqrt{2} \int_0^{\pi/2} \sin^5 \theta d \theta \nonumber\]

і складність пішла. Читач повинен спробувати інтегрувати це чисельно за правилом Сімпсона, хоча також можна відзначити, що він має точну аналітичну відповідь, а саме\(\sqrt{8192}/15\).

Ось ще один приклад. Можна показати, що період коливання простого маятника довжини, що\(l\) розгойдується\(90^\circ\) по обидва боки вертикалі, дорівнює

\[P = \sqrt{\frac{8l}{g}} \int_0^{\pi/2} \sqrt{\sec \theta} d\theta . \nonumber\]

Як і в попередньому прикладі, integrand стає нескінченним на верхній межі. Я залишаю читачеві знайти відповідну зміну змінної таким чином, що integrand є кінцевим в обох межах, а потім інтегрувати його чисельно. (Якщо ви здаєтеся, див. Розділ 1.13.) На відміну від останнього прикладу, цей не має простого аналітичного рішення з точки зору елементарних функцій. Це може бути записано з точки зору спеціальних функцій (еліптичних інтегралів), але вони повинні бути оцінені чисельно в будь-якому випадку, так що це мало допомагає. Я роблю відповідь

\[P = 2.3607 \pi \sqrt{\frac{l}{g}} . \nonumber\]

Для іншого прикладу розглянемо

\[\int_0^\infty \frac{dx}{x^5 \left( e^{1/x} - 1\right)}\nonumber\]

Цей інтеграл зустрічається в теорії випромінювання чорноготіла. Щоб допомогти вам візуалізувати integrand, він і його перша похідна дорівнює нулю при\(x = 0\)\(x = \infty\) і вона досягає максимального значення\(21.201435\) at\(x = 0.201405\). Складність цього разу - нескінченна верхня межа. Але, як і в попередніх двох прикладах, ми можемо подолати труднощі, зробивши зміну змінної. Наприклад, якщо ми дозволимо\(x = \tan \theta\), інтеграл стає

\[\int_0^{\pi/2} \frac{c^3 \left(c^2 + 1 \right) d\theta}{e^c - 1}, \text{where } c=\cot \theta = 1/x. \nonumber\]

Integrand дорівнює нулю в обох межах і легко обчислюється між ними, і значення інтеграла тепер можна обчислити за правилом Сімпсона простим способом. Він також має точне аналітичне рішення\(\pi^4 /15\), а саме, хоча важко сказати, чи легше досягти цього шляхом аналізу або числового інтегрування.

Ось ще:

\[\int_0^\infty \frac{x^2 dx}{(x^2+9)(x^2+4)^2} \nonumber\]

Безпосередньою складністю є нескінченна верхня межа, але з цим легко впоратися, зробивши зміну змінної:\(x = \tan \theta\). Інтеграл тоді стає

\[\int_{\theta=0}^{\pi/2} \frac{t(t+1)d\theta}{(t+9)(t+4)^2} \nonumber\]

в якому\(t = \tan^2 \theta\). Верхня межа тепер кінцева, а integrand легко обчислити - крім, мабуть, верхньої межі. Однак після деяких початкових коливань читач, ймовірно, погодиться, що integrand дорівнює нулю у верхній межі. Цілісний вигляд виглядає так:

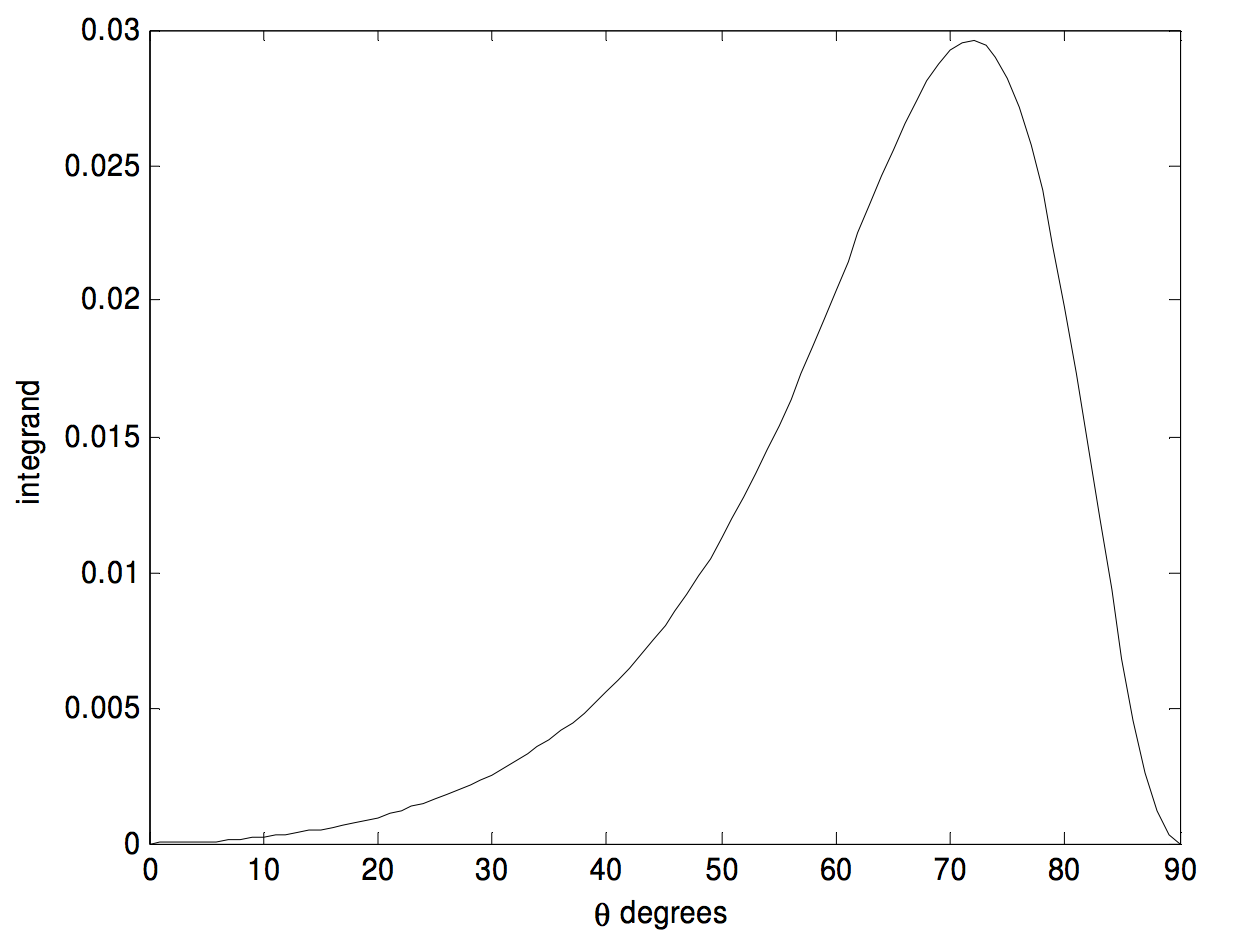
Він досягає максимуму\(0.029 \ 5917\) при\(\theta = 71^\circ .789 \ 962\). Правило Сімпсона легко дало мені відповідь\(0.015 \ 708\). Інтеграл має аналітичне рішення (спробуйте)\(\pi/200\).

Існують, звичайно, методи чисельного інтегрування, відмінні від правила Сімпсона. Я описую один тут без доказів. Я називаю це «семиточкова інтеграція». Це може здатися складним, але як тільки ви успішно запрограмували його для комп'ютера, ви можете забути деталі, і це часто навіть швидше і точніше, ніж правило Сімпсона. Ви оцінюєте функцію в\(6n + 1\) точках,\(n\) де ціле число, щоб були\(6n\) інтервали. Якщо, наприклад\(n = 4\), ви оцінюєте функцію в\(25\) точках, включаючи нижню і верхню межі інтеграції. Інтеграл тоді:

\[\int_a^b f(x)dx = 0.3 \times (\Sigma_1 + 2 \Sigma_2 + 5 \Sigma_3 + 6\Sigma_4)δx, \label{1.2.9}\]

де\(δx\) - розмір інтервалу, а

\[\Sigma_1 = f_1 + f_3 + f_5 + f_9 + f_{11} + f_{15} + f_{17} + f_{21} + f_{23} + f_{25} , \label{1.2.10}\]

\[\Sigma_2 = f_7 + f_{13} + f_{19} , \label{1.2.11}\]

\[\Sigma_3 = f_2 + f_6 + f_8 + f_{12} + f_{14} + f_{18} + f_{20} + f_{24} \label{1.2.12}\]

і\[\Sigma_4 = f_4 + f_{10} + f_{16} + f_{22} . \label{1.2.13}\]

Ось, звичайно,\(f_1 = f(a)\) і\(f_{25} = f(b)\). Ви можете спробувати це на функціях, які ми вже інтегрували за правилом Сімпсона, і подивитися, чи це швидше.

Давайте спробуємо одну останню інтеграцію, перш ніж перейти до наступного розділу. Давайте спробуємо

\[\int_0^{10} \frac{1}{1+8x^3} dx . \nonumber\]

Це може легко (!) бути інтегрованим аналітично, і ви можете показати, що це

\[\frac{1}{12} \ln \frac{147}{127} + \frac{1}{\sqrt{12}} \tan^{-1} \sqrt{507} + \frac{\pi}{\sqrt{432}} = 0.6039748 . \nonumber\]

Однак наша мета в цьому розділі - навчитися деяким навичкам числового інтегрування. Використовуючи правило Сімпсона, я отримав вищевказану відповідь до семи знаків після коми з\(544\) інтервалами. Однак при семиточковій інтеграції я використовував лише\(162\) інтервали для досягнення тієї ж точності, зменшення\(70%\). Так чи інакше, розрахунок на швидкому комп'ютері був майже миттєвим. Однак якби це була дійсно тривала інтеграція, більша ефективність інтеграції з семи точок могла б заощадити години. Також варто відзначити,\(x \times x \times x\) що обчислити швидше, ніж\(x^3\). Крім того, якщо ми зробимо підстановку y = 2x, інтеграл стає

\[\int_0^{20} \frac{0.5}{1+y^3} dy . \nonumber\]

Це зменшує кількість множень, які потрібно зробити від\(489\) до\(326\) — тобто подальше зменшення на третину. Але ми все ще не зробили все, що могли зробити. Давайте подивимося на функцію\(\frac{0.5}{1+y^3}\), на малюнку i.2b:

\(\text{FIGURE I2b}\)

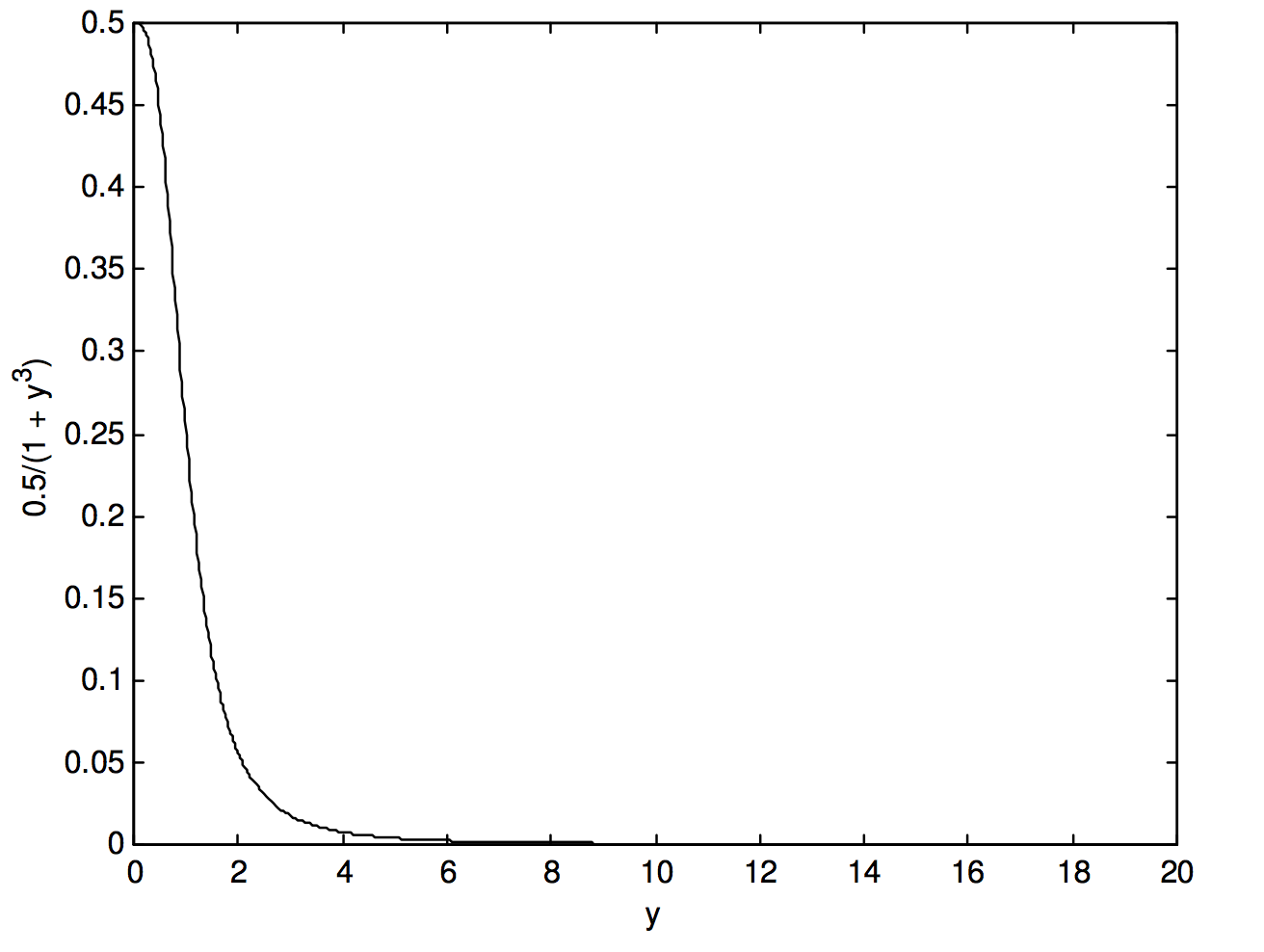
Ми бачимо, що крім того\(y = 6\), наші зусилля були значною мірою витрачені даремно. Нам не потрібні такі тонкі інтервали інтеграції. Я вважаю, що я можу отримати той самий рівень точності - тобто відповідь\(0.6039748\) - використовуючи 48 інтервалів від\(y = 0\) до\(6\) та\(24\) інтервалів від\(y = 6\) до\(20\). Таким чином, різними способами ми зменшили кількість разів, що функція повинна була бути оцінена від нашого оригіналу\(545\) до\(72\), а також зменшуючи кількість множень кожного разу на третину, скорочення часу обчислення на\(91%\). Цей останній приклад показує, що часто вигідно використовувати тонкі інтервали інтеграції лише тоді, коли функція швидко змінюється (тобто має великий нахил), і повертатися до більш грубих інтервалів, де функція змінюється лише повільно.

Гауссовий квадратурний метод чисельного інтегрування описаний в розділах 1.15 і 1.16.