1.14: Многочлени Лежандра

Last updated
Save as PDF

Page ID: 78058

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Розглянемо вираз

\[(1-2rx + r^2 ) ^{-1/2} , \label{1.14.1} \tag{1.14.1}\]

в якому\(|x|\) і\(|r|\) обидва менше або рівні одиниці. Подібні до цього вирази зустрічаються досить часто в теоретичній фізиці - наприклад, при обчисленні гравітаційних або електростатичних потенціалів тіл довільної форми. Див., наприклад, главу 5, розділи 5.11 і 5.12.

Розгорніть\(\ref{1.14.1}\) вираз біноміальною теоремою як ряд степеней\(r\). Це просто, хоча і не особливо легко, і ви можете розраховувати витратити кілька хвилин на отримання коефіцієнтів перших кількох повноважень\(r\). Ви виявите, що коефіцієнт of\(r^l\) - це поліноміальний вираз в\(x\) градусі\(l\). Дійсно, розширення набуває форми

\[(1 - 2rx + r^2 )^{-1/2} = P_0 (x) + P_1 (x) r + P_2 (x) r^2 + P_3 (x) r^3 ... \label{1.14.2} \tag{1.14.2}\]

Коефіцієнти послідовної степені\(r\) - це многочлени Лежандра; коефіцієнт\(r^l\), який є\(P_l(x)\), є поліномом Лежандра порядку\(l\), і він є поліномом у\(x\) включенні членів настільки ж високим, як\(x^l\). Ми вводимо ці многочлени в цьому розділі, тому що вони нам знадобляться в Розділі 1.15 про виведення гаусової квадратури.

Якщо ви сумлінно намагалися розширити вираження\(\ref{1.14.1}\), ви виявите, що

\[P_0 (x) = 1, \quad P_1 (x) = x, \quad P_2 (x) = \frac{1}{2} (3x^2 - 1), \label{1.14.3} \tag{1.14.3}\]

хоча ви, напевно, відмовилися від виснаження після цього і не взяли його далі. Якщо ви уважно подивитеся на те, як ви вивели перші кілька многочленів, ви, можливо, виявили для себе, що ви можете отримати наступний многочлен як функцію двох попередніх многочленів. Можливо, ви навіть виявили для себе наступне відношення рекурсії:

\[P_{l+1} = \frac{(2l+1)xP_l - lP_{l-1}}{l+1}. \label{1.14.4} \tag{1.14.4}\]

Це дозволяє нам дуже швидко отримати поліноми Лежандра вищого порядку, будь то чисельно або в алгебраїчній формі. Наприклад, поставити\(l = 1\) і показати, що Рівняння 1.12.4 призводить до\(P_2 = \frac{1}{2} (3x^2 - 1)\). Вам потім захочеться прорахувати\(P_3\), а потім\(P_4\), і все більше і більше. Інший спосіб їх генерувати - це формувати рівняння

\[P_{l+1} = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2 - 1)^l . \label{1.14.5} \tag{1.14.5}\]

Ось перші одинадцять многочленів Лежандра:

\ begin {масив} {l}
P_0 = 1\\
P_1 = х\\
P_2 =\ розриву {1} {2} (3x^2 - 1)\\
P_3 =\ розриву {1} {2} (5x^3 - 3x)\\
P_4 =\ розриву {1} {8} (35х^4 - 30х^2 + 3)\\
P_5 =\ гідророзрив {1} {16} (63х^5 - 70х^3 + 15x)\\
P_6 =\ гідророзриву {1} {16} ( 231x^6 - 315х^4 + 105х^2 - 5)\\
P_7 =\ розрив {1} {16} (429х^7 - 693х^5 + 315х^3 -35x)\\
P_8 =\ розрив {1} {128} (6435х^8 - 12012х^6 + 6930х^4 -1260x^2 + 35\\
P_9 =\ розрив {1} {128} (12155x^9 - 25740x^7 + 18018x^5 - 4620x^3 + 315x)\\
P_ {10} =\ розрив {1} {256} ( 46189 x^ {10} - 109395x^8 + 90090х^6 - 30030x^4 + 3465x^2 - 63)\
\ мітка {1.14.6}\ тег {1.14.6}
\ кінець {масив}

Поліноми з аргументом\(\cos \theta\) наведені в розділі 5.11 глави 5.

У наступному розділі ми також хочемо знати коріння Рівняння\(P_l = 0\) для\(l > 1\). Огляд форм цих многочленів швидко покаже, що всі непарні многочлени мають корінь нуля, а всі ненульові корені зустрічаються в позитивні/негативних парах. Прочитавши розділи 1.4 і 1.5, ми не матимемо труднощів у пошуку коренів цих Рівнянь. Коріння\(x_{l,i}\) наведені в наступній таблиці, де також перераховані певні коефіцієнти\(c_{l,i}\), які будуть пояснені в розділі 1.15.

коріння\(P_l = 0\)

\ begin {масив} {c c}
л & x_ {l, i} & c_ {л, я}\\
\
2 &\\\ 2 &\\ пм 0.577\ 350\ 190 & 1.000\ 000\ 000\ 00\\
\\
3 &\\ пм 0,774\ 596\ 669\ 241\ 555\ 555\ 555\ 555\ 56\
& 0.000 000\\ 000 000 & 0.888\ 888\ 888\ 89\\\
\
4 &\\ pm 0.861\ 136\ 311\ 594 & 0.347\ 854\ 845\ 14\\\
&\ pm 0,339\ 981\ 043\ 585 & 0,652\ 154\ 86\\\\
\
5 &\ пм 0,906\ 179\ 845\ 939 & 0,236\ 926\ 885\ 06\\
&\ Пм 0,538\ 469\ 310\ 106 & 0,478\ 628\ 670\ 50\\\
& 0.000\ 000\ 000 & 0.568\ 888\ 888\ 89\\\
\
6 &\ pm 0,932\ 469\ 514\ 203 & 0.171\ 324\ 492\ 38\\
& pm 0,661\ 209\ 386\ 466 & 0,360\ 761\ 573\ 05\\\
&\ вечора 0,238\ 619\ 186\ 083 & 0,467\ 913\ 934\ 57\\\
\
7 &\\ пм 0,949\ 107\ 912\ 343 & 0,129\ 484\ 966\ 17\\\
&\ пм 0,741\ 531\ 185\ 599 & 0,279\ 705\ 391\ 49\\
&\ пм 0,405\ 845\ 151\ 377 & 0,381\ 830\ 050\ 50\\
& 0,000\ 000\ 000 & 0,417\ 959\ 183\ 68\\\\
8 &
\\ пм 0,960\ 289\ 856\ 498 & 0,101\ 228\ 536\ 29\\\\
& пм 0,796\ 666\ 477\ 414 & 0,222 \ 381\ 034\ 45\\\
&\ Пм 0,525\ 532\ 409\ 916 & 0,313\ 706\ 645\ 88\\\
&\ вечора 0,183\\ 434\ 642\ 496 & 0,362\ 683\ 783\ 38\\
\\
9 &\ пм 0,968\ 160\ 239\ 508\ 0,081\ 274\ 388\ 36\
&\ вечора 0 .836\ 031\ 107\ 327 & 0,180\ 648\ 160\ 69\\
&\ вечора 0.613\ 371\ 432\ 701 & 0.260\ 610\ 696\ 40\\
&\\ pm 0,324\ 423\ 404 & 0,312\ 347\ 077\ 04\\
& 0,000 000 000\ 000\ 000\ 0,330\ 239\ 355\ 00\\
\ \
10 &\ вечора 0.973\ 906\ 528\ 517 & 0.066\ 671\ 343\ 99\\ &\\
&\\ &\\ вечора 0,865\ 063\ 366\ 689 & 0.149\ 451\ 349\ 64\\
&\ pm 0,679\ 568\ 299\ 086\ 362\ 24\\
&\ pm 0,433\ 395\ 394\ 129 & 0,269\ 266\ 719\ 47\\\
&\ вечора 0,148\ 874\ 338\ 982 & 0,295\ 524\ 224\ 66\
\\
11\\ пм 0,978\ 658\ 146 & 0,055\ 668\ 567\ 12\\
&\\ пм 0,887\ 062\ 599\ 768 & 0,125\ 580\ 369\ 46\\\
&\ пм 0. 730\ 152\ 005\ 574 & 0,186\ 290\ 210\ 93\\
&\\\ вечора 0,519\ 096\ 129\ 207 & 0,233\ 764\ 59\\\
&\ пм 0,269\ 543\ 155\ 952 & 0,262\ 804\ 544\ 51\\
& 0,000\ 000\ 000\ 000\\ 0,272\ 086\ 78\\
\\
12 &\ вечора 0,981\ 560\ 634\ 247 & 0,047\ 175\ 336\ 39\\\
&\ вечора 0.904\ 117\ 256\ 370 & 0.106\ 939\ 325\ 99\\
&\\ вечора 0,769\ 902\ 674\ 194 & 0.160\ 328\ 54\\
&\ pm 0,587\ 317\ 954\ 954\ 954\ 957\ 287 & 0.203\ 167\ 426\ 72\\\
&\ вечора 0,367\ 831\ 498\ 998 & 0,233\ 492\ 536\ 54\\\ &\ пм 0,125\ 233\ 408\ 511
& 0,249\ 147\ 045\ 81\\\\
13 &\ пм 0,984\ 183\ 054
\ 719 & 0,040\ 004\ 77\\\\\ пм 0,984\ 183\ 054\ 719\ 484\ 004\ 77\\\
\\ пм 0. 917\ 598\ 399\ 223 & 0,092\ 121\ 499\ 84\\
&\ вечора 0,801\ 578\ 090\ 733 & 0,138\ 873\ 510\ 22\\ &\\ пм 0,642\ 349\ 339\ 440
& 0,178\ 980\ 76\\\ &\ пм 0,448\ 492\ 751\ 036\
880\ 880\ 76\\ пм 0,448\ 492\ 751\ 036\ 8207 16\ 047\ 54\\
&\ вечора 0.230\ 458\ 315\ 955 & 0.226\ 283\ 180\ 26\\
& 0.000\ 000\ 000\ 000 & 0.232\ 551\ 553\\ 23\
\\\
14 &\\ pm 0,986\ 283\ 808\ 697 & 0.035\ 460\ 33\\
\\ pm 0,928\ 434\ 883\ 664 & 0.080 \ 158\ 087\ 16\\\
&\ вечора 0,827\ 201\ 315\ 070 & 0,121\ 518\ 570\ 69\\\
&\\\ вечора 0,687\ 904\ 812 & 0,17\ 203\ 167\ 16\\
&\ вечора 0.515\ 636\ 358 & 0.185\ 538\ 397\\\\
&\\ pm 0.319\ 112\ 368\ 928 & 0,205\ 198\ 463\ 72\\\
&\ вечора 0,18\ 054\ 948\ 707 & 0,215\ 263\ 853\\ 46\\
\
15 &\ пм 0,987\ 992\ 518\ 020 & 0,030\ 753\ 242\ 00\\
&\ пм 0,937\ 273\ 392\ 401 & 0,070\ 366\ 047\ 49\\
&\ вечора 0.848\ 206\ 583\ 410 & 0.107\ 159\ 220\ 47\\
&\ вечора 0.724\ 417\ 731\ 360 & 0.139\ 570\ 677\ 93\\
&\\ pm 0.570\ 972\ 172\ 609 & 0.166\ 205\ 82\\
&\ pm 0.394\ 151\ 347\ 078\ 0.186\ 161 \ 000\ 02\\\
&\ вечора 0.201\ 194\ 093\ 997 & 0.198\ 431\ 485\ 33\\\
& 0.000\ 000\ 000 & 0.202\ 578\ 241\ 92\\\
\
16 &\ pm 0,989\ 400\ 934\ 992 & 0,027\ 152\ 459\ 41\\
&\\\ pm 0,944\ 575\ 023\ 073 & 0,062\ 253\ 523\ 94\\
&\ вечора 0,865\ 631\ 202\ 388\ 158\ 511\ 68\\\
&\ пм 0,755\ 408\ 408\ 355 & 0,124\ 628\ 971\ 26\\
&\ пм 0,617\ 876\ 244\ 403 & 0.149\ 595\ 995\ 88\ 82\\
& ;\ вечора 0,458\ 016\ 777\ 657 & 0.169\ 156\ 519\ 39\\
&\\ &\ вечора 0.281\ 603\ 550\ 779 & 0.182\ 603\ 415\ 04\\
&\ pm 0,095\ 012\ 509\ 838 & 0.189\ 450\ 610\ 46\\\
\
17 &\ pm 0,990\ 575\ 475\ 315 & 0,024\ 148\ 302\ 87\\\
&\ вечора 0,950\ 675\ 521\ 769 & 0,055\ 459\ 529\ 38\\\\
&\ вечора 0,880\ 239\ 153\ 727 & 0,085\ 036\ 148\ 32\\
&\\ пм 0,781\ 514\ 003\ 897 & 0,111\ 883\ 847\ 19\\\
& Пм 0,657\ 671\ 159\ 217 & 0,135\ 136\ 368\ 47\\\
&\ вечора 0.512\ 690\ 537\ 086 & 0.154\ 045\ 761\ 08\\
&\ вечора 0.351\ 763\ 454 & 0.168\ 004\ 102\\\\
&\\\ pm 0.178\ 484\ 181\ 496 & 0.176 000\ 562\ 705\ 37\\\\
& 0.000\ 000\ 000 & 0.179\ 446\ 470\ 35\\
\ кінець {масив}

Для інтересу малюю графіки многочленів Лежандра в цифрах\(\text{I.7}\) і\(\text{I.8}\).

Малюнок\(\text{I.7}\). Многочлени Лежандра для парних\(\text{I}\)
альт

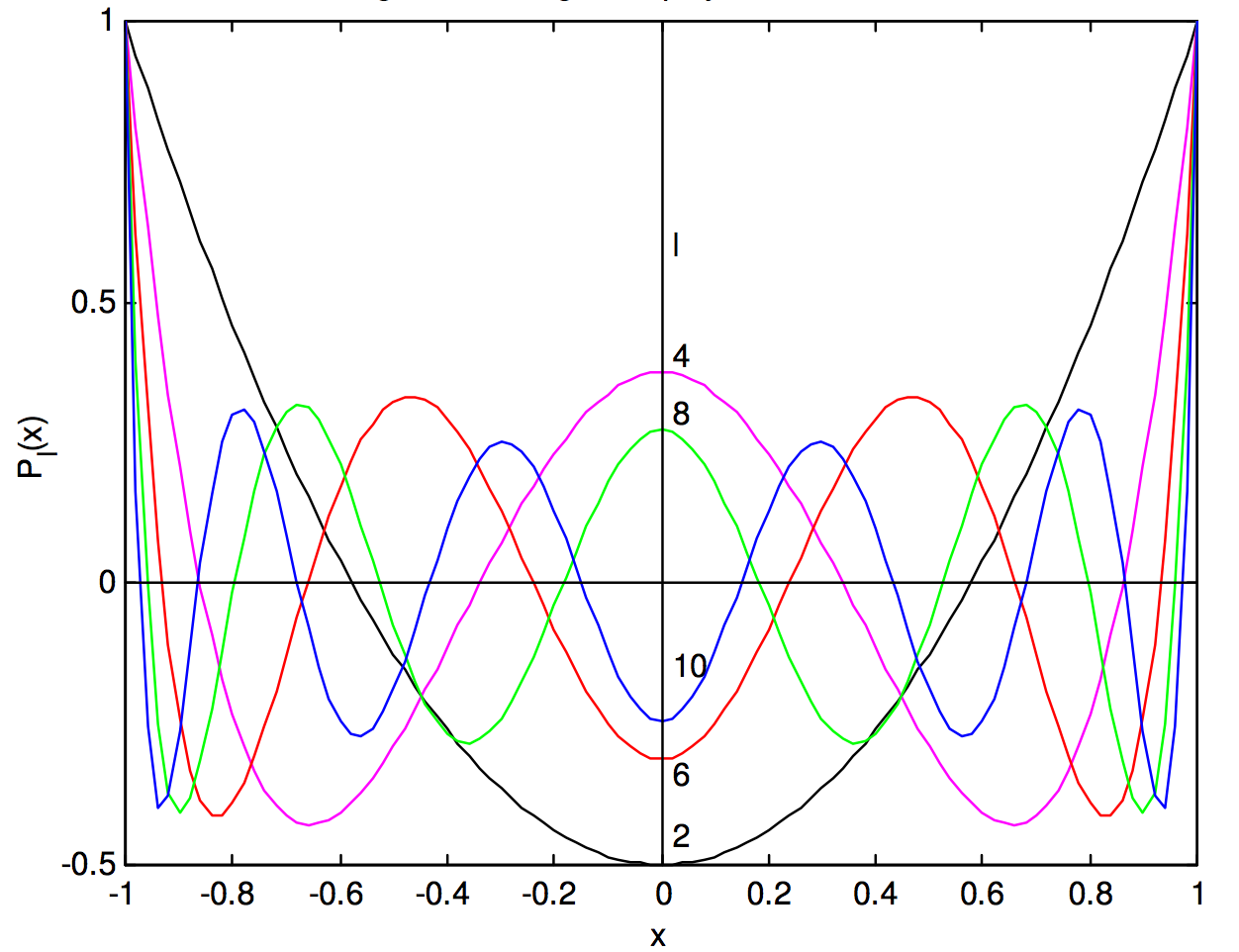
Малюнок\(\text{I.8}\). Многочлени Лежандра для непарних\(\text{I}\)
альт

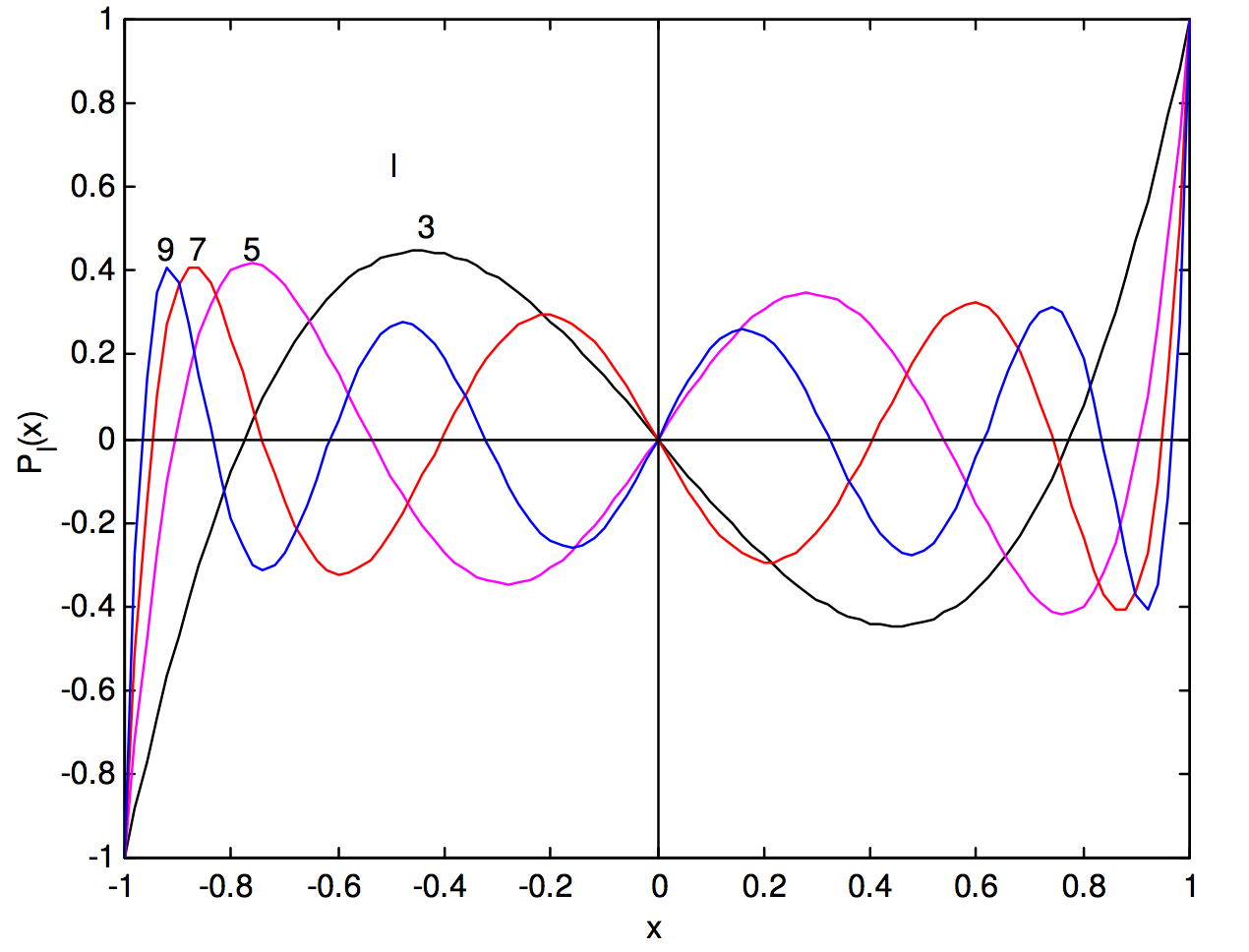
Для подальшого інтересу слід легко перевірити шляхом підстановки, що поліноми Лежандра є розв'язками диференціального рівняння

\[(1-x^2)y^{\prime \prime} - 2xy^\prime + l(l+1) y = 0. \label{1.14.7} \tag{1.14.7}\]

Поліноми Лежандра - це розв'язки цього та пов'язаних рівнянь, які з'являються при вивченні коливань твердої сфери (сферичні гармоніки) та у розв'язанні рівняння Шредінгера для воднеподібних атомів, і вони відіграють велику роль у квантовій механіці.