7.21: Ефект Зеємана

Коли гарячий газ, який випромінює або поглинає спектральні лінії, поміщається в магнітне поле, лінії розщеплюються на кілька компонентів. Це відомо як ефект Зеемана, відкритий в 1896 році голландським спектроскопістом П.Зееманом.

Якщо ми почнемо з мислення атома з нульовим ядерним спіном, буде нагадано, що кожен енергетичний рівень, крім тих, що мають,$J = 0$ вироджується. Тобто існують$2J + 1$ хвильові функції, або власні стани, або просто стани, кожен з яких описується квантовим числом$M$, яке йде від$−J$ до$+J$, і кожне з цих станів має точно таку ж енергію. При поміщенні атома в зовнішнє магнітне поле це виродження видаляється, і кожен стан має трохи різну енергію. Це відбувається з обома рівнями, які беруть участь у формуванні лінії (якщо тільки один з рівнів не має$J = 0$), в результаті чого лінія, яка з'єднує два рівні, розділяється на ряд компонентів. Нагадаємо, що лінія з'єднує два рівні. Аналогічним чином компонент (Zeeman) приєднується до двох станів. Так само, як множник - це сукупність рядків, що з'єднують два члени, так і лінія - це сукупність компонентів, що з'єднують два рівні. При відсутності магнітного поля всі стани всередині рівня мають однакову енергію, а всі складові, що складають лінію, мають однакову довжину хвилі. Термін описується$LS$. Його кратність є$2 \text{min} \left\{ L , S \right\} +1$ і його статистична вага$(2L +1)( 2S +1)$. Рівень описується$LSJ$. Його виродження і статистична вага є$2J + 1$. Стан описується$LSJM$. Він не вироджений; його статистична вага є$1$.

У розділах 9, 10 і 11 цієї глави я пішов на деякі труднощі, щоб переконати вас, що електрон - це не тверда прядильна сфера, яка рухається по круговій орбіті навколо ядра. Швидше я описав електрони в терміні хвильових функцій, які описують амплітуду ймовірностей, а квантові числа були власними значеннями певних операторів і були обмежені певними значеннями в результаті граничних умов. Яку модель ми використовуємо для опису поведінки атомів, залежить від нашої мети, і, якби нашою метою було отримати досвід у тонкощах квантових механічних обчислень, нам довелося б активно брати участь в алгебрі кетів, операторів і власних функцій. Однак наша теперішня мета полягає в тому, щоб ознайомитись досить описовим способом зі спектроскопією та описом явищ Зеемана без наміру виконувати квантові механічні розрахунки. Буде зручно повернутися до моделі електрона, якщо не як тверда, обертається, орбітальна частинка, принаймні як сутність, яка має атрибути орбітального та спінового кутового імпульсу, а отже, і магнітного моменту.

Зокрема, нагадаємо, що орбітальний електрон має орбітальний момент моменту$\sqrt{l(l +1)}\hbar$, де$\hbar=h/(2\pi )$ має значення$1.055 \times 10^{−34} \text{J s}$. Тепер, якщо взяти магнітогиричне відношення орбітального електрона бути$e/ (2m)$, магнітний момент орбітального електрона є$\sqrt{l(l+1)}\cdot \dfrac{e \hbar}{2m}$. (Ті, хто заперечує проти цього простого лікування - і є деякі досить очевидні заперечення - не матимуть альтернативи, окрім як зробити належну квантову механічну деривацію, хоча результат однаковий.) У будь-якому випадку величина$\dfrac{e\hbar}{2m}$, одиниця магнітного моменту, називається магнетоном Бора, а його значення -$9.274 \times 10^{−24} \ \text{N m T}^{−1}$ або$\text{A m}^2$. Я використовую символ$\mu_B$ для позначення магнетона Бора. Таким чином, орбітальний момент імпульсу електрона є$\sqrt{l(l +1)}\hbar$ і його магнітний момент є$\sqrt{l(l+1)}\mu_B$ Магнітогирическое відношення орбітального електрона (не беручи до уваги внесок в кутовий імпульс і магнітний момент від його спіна)$\mu_B / \hbar = e/ (2m) = 8.794 \times 10^{10} \ \text{C kg}^{-1}$, або, якщо ми згодні висловити Кутовий імпульс в одиницях$\hbar$ і магнітний момент в одиницях магнетонів Бора, магнітогирическое відношення орбітального електрона (все ще не враховуючи внески спіна) становить$1$. Спіновий кутовий імпульс електрона є$\sqrt{s(s+1)}\hbar$, де$s =1/2$, і його магнітний момент (дуже близький до)$2\sqrt{s(s+1)}\hbar$, так що його магнітогирическое відношення є справедливим$e/m$, або, в одиницях$\mu$ і$\hbar$, це$2$. (Точне значення магнітогирического відношення, в одиницях$\mu_B / \hbar$, трохи більше$2$, і є однією з найбільш точно відомих з фундаментальних фізичних констант. Його значення в 2000 році дається як 2,002 319 304 374.)

При обговоренні ефекту Зеемана нам потрібно знати магнітогирическое співвідношення атома на заданому рівні, оскільки це визначає спосіб розщеплення рівнів в магнітному полі. Ставлення магнітного моменту в одиницях моменту$\mu_B$ до моменту моменту в одиницях відоме як коефіцієнт розщеплення Ланде і, як правило, позначається символом$g$.$\hbar$ Це магнітогирическое відношення в одиницях$e/(2m)$, або$8.794 \times 10^{10} \ \text{C kg}^{-1}$. Магнітогиричне відношення, або коефіцієнт розщеплення Ланде атома на заданому рівні залежить від кута між векторами$\textbf{L}$$\textbf{S}$ і, отже$\textbf{J}$, від їх результуючої, і, хоча я цього не роблю тут, неважко показати, що у випадку$LS$ -зчеплення Ланде коефіцієнт розщеплення має значення

$$g = 1 + \dfrac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)}. \label{7.21.1} \tag{7.21.1}$$

(Ця формула розраховується з використанням$2$ наближеного значення магнітогиричного співвідношення електрона, а не більш точного$2.00232$. Точніше, вона повинна бути написана

$$g = 1 + 1.00232 \dfrac{J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}. \label{7.21.2} \tag{7.21.2}$$

Формули для$g$ -фактора для інших схем зв'язку є, але я їх тут не наводжу, так як на практиці зв'язок між електронними кутовими моментами в складних атомах зазвичай є проміжною між ідеалізованими крайностями, і розрахунок доводиться робити чисельно. Однак у багатьох найлегших атомах чиста$LS$ -зв'язок є хорошим наближенням. $g$Значення -можна знайти експериментально зі спостережень ефекту Зеемана, і, на додаток до правила інтервалу Ланде, згаданого раніше, це дає ще одне хороше вказівку на те, наскільки близький рівень до$LS$ -зчеплення.

Проблема. $^5 \text{P}_1 - \ ^5 \text{D}_0^\text{o}$Лінія$\text{Fe}_\text{ I}$ at часто$617.33 \ \text{nm}$ використовується для дослідження магнітних полів у сонячних плямах. Найсильніша лінія мультиплету, що включає цей рядок, є$^5\text{P}_3 - \ ^5 \text{D}_4^\text{o}$. Обчисліть$g$ -фактор для кожного з чотирьох згаданих рівнів.

Невеликий момент, який слід зробити, полягає в наступному. З того, що ми говорили, магнітний момент атома (виключаючи ядерний спін, якщо такий є) має величину$\mu = g\mu_B \sqrt{J (J +1)}$. (Це випливає з визначення того$g$, яке відношення магнітного моменту в одиницях магнетона Бора - тобто$\mu/\mu_B$ - до мотового моменту в одиницях$\hbar$.) У векторній формі це повинно бути записано$\boldsymbol{\mu} = −g \mu_B \textbf{J}$, де$\textbf{J}$ безрозмірний вектор величини$\sqrt{J(J +1)}$ і знак мінус виникає через негативного електронного заряду, причому вектори магнітного моменту і кутового імпульсу спрямовані протилежно.

Коли ефект Зеемана був вперше досліджений, лінії були розділені лише на три компоненти, і це називалося нормальним ефектом Зеемана. Пізніше спостерігалися більш складні закономірності, і це називалося аномальним ефектом Зеемана. Як ми зараз це розуміємо, так званий «нормальний» ефект Зеемана - це лише ефект Зеемана, який спостерігається на лініях, що з'єднують рівні зі спином$S = 0$, які мають простіший візерунок Зеемана, ніж інші лінії. Крім експерименту Штерна-Герлаха, саме вивчення «аномального» розщеплення Зеемана породило відкриття електронного спіна.

Зараз ми можемо почати дивитися на те, як розділяються рівні енергії при наявності магнітного поля. Розглянемо, наприклад,$^1 \text{P}_1$ рівень ($L, \ S, \ J = 1, 0, 1$). Фактор Ланде є$1$. (Зверніть увагу, що для будь-якого рівня, в якому S = 0 і, отже, в якому$J$ і$L$ обов'язково рівні, Equation$\ref{7.21.1}$ (або\ ref {7.21.2}) показує це$g = 1$.)

Магнітний момент є$\boldsymbol{\mu} = −g \mu_B \textbf{J} = −\mu_B \textbf{J}$. Енергія магніту - це магнітне поле є$−\boldsymbol{\mu} \cdot \textbf{B}$, тому в даному випадку воно є$\mu_B \textbf{J}\cdot \textbf{B}$. Але$\textbf{J}\cdot \textbf{B}$ дорівнює$B$ раз складової$\textbf{J}$ в ту сторону$\textbf{B}$, яка є$M$. Таким чином, енергія стану$M$ в магнітному полі є$\mu_B MB$. Існує три значення$M \ (−1, \ 0, \ 1)$. Розщеплення рівня на три його стану лінійно пропорційно магнітному полю$B$, а поділ між сусідніми станами -$\mu_B B$.

Якщо розглядати$^1 \text{D}_2$ рівень, знову ж таки$g = 1$, і держави мають однаковий інтервал, за винятком того, що цього разу є п'ять станів, з$M = −2$ до$+2$.

Тепер розглянемо рядок$^1 \text{P}_1 − \ ^1 \text{D}_2$. Це сукупність всіх переходів, що з'єднують три стани в одному з п'ятьма станами в іншому. Не всі переходи можливі, однак, тому в лінійці немає п'ятнадцяти складових. Правила вибору (які будуть розглянуті в розділі 7.24) обмежують тільки можливі переходи до тих, для яких$\Delta M = 0$ або$\pm 1$. На малюнку VII.1 показані енергетичні рівні восьми станів і дев'ять можливих переходів, які їх з'єднують.

Буде видно, що дев'ять компонентів знаходяться в трьох групах по три, і що, оскільки відстані на двох рівнях однакові (що, в свою чергу, є результатом$S = 0$), всі три лінії в даній групі мають точно таку ж довжину хвилі (хоча я їх трохи розділив). Отже, ви побачите в спектрі, мабуть, лише три компоненти Zeeman, повний

$\text{FIGURE VII.1}$

дев'ять не будучи повністю відокремлені. Це те, що називалося «нормальним» ефектом Зеемана. Однак$S \neq 0$, як тільки$g$ -значення двох рівнів будуть різними, інтервали станів на двох рівнях будуть різними, всі компоненти будуть повністю розділені, і ми бачимо «аномальний» ефект Зеемана, хоча насправді нічого аномального в цьому немає. У певному сенсі «нормальний» ефект Зеемана є винятковим. На малюнку$\text{VII.2}$ я намалював схематично (із збільшенням довжини хвилі лінійно вправо) візерунок Зеемана для$^2 \text{S}_{\dfrac{1}{2}} - \ ^2 \text{P}_{\dfrac{3}{2}}$. Коефіцієнти розщеплення для$\text{S}$ рівнів$\text{P}$ і є, відповідно,$2$ і$4/3$. Буває, що в цьому випадку всі шість компонентів Zeeman однаково розташовані, хоча це не завжди так; точний шаблон компонентів Zeeman варіюється від рядка до рядка.

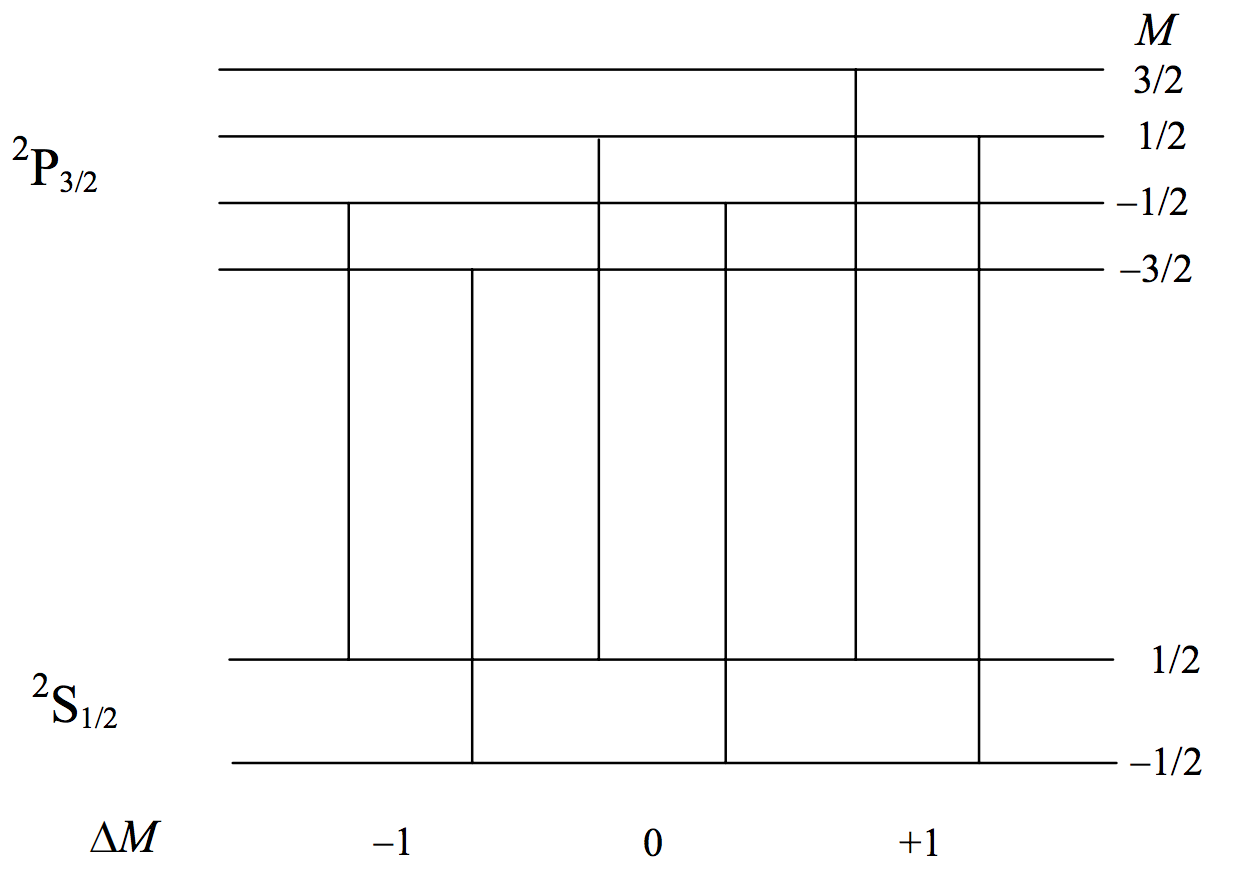
$\text{FIGURE VII.2}$