32.1: Комплексні числа
- Page ID
- 26787
Реальні числа
Давайте подумаємо про звичайні числа, викладені на лінії, яка йде до нескінченності як в позитивному, так і в негативному напрямках. Ми могли б почати з взяття розтягнення лінії біля початку (тобто точка, що представляє число нуль) і покласти в цілі числа наступним чином:

Далі, ми могли б додати в раціональні числа, такі як ½, 23/11 і т.д., то ірраціональні\(\sqrt{2}\), як, потім числа\(\pi\), як, і так далі, так що будь-яке число ви можете думати про має своє місце на цьому рядку. Тепер давайте візьмемо трохи іншу точку зору, і думати про числа, як представлені вектором від походження до цього числа, так що 1
і, наприклад, —2 представлений:

Зверніть увагу, що якщо число помножити на —1, відповідний вектор повертається на 180 градусів. У картинках,
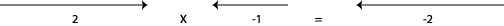
«Вектор» 2 повертається\(\pi\), або 180 градусів, коли ви помножите його на —1.
Які квадратні коріння у 4?
Рішення
Ну, 2, очевидно, але також —2, тому що множення вектора зворотного вказівки —2 на —2 не тільки подвоює його довжину, але й повертає його на 180 градусів, тому тепер він вказує в позитивному напрямку. Ми, здається, винайшли важкий спосіб заявити, що множення двох негативів дає позитив, але мислення з точки зору повороту векторів через 180 градусів окупиться незабаром.
Розв'язування квадратних рівнянь
При розв'язанні стандартного квадратного рівняння
\[ax^2 + bx + c = 0 \label{A.1} \]
ми знаходимо рішення бути:
\[ x =\dfrac{-b \pm \sqrt{b^2-ac}}{2a} \label{A.2} \]
Проблема з цим полягає в тому, що іноді вираз всередині квадратного кореня є негативним. Що це означає? Для деяких проблем у фізиці це означає, що рішення не існує. Наприклад, якщо я кидаю м'яч прямо вгору на 10 метрів в сек, і запитати, коли він досягне висоти 20 метрів, приймаючи g = 10 м за сек 2, рішення квадратного рівняння за час t має негативне число всередині квадратного кореня, а це означає, що м'яч не добирається до 20 метрів, тому питання насправді не має сенсу.
Однак ми виявимо, що є й інші проблеми в широких областях фізики, де негативні числа всередині квадратних коренів мають важливе фізичне значення. З цієї причини нам потрібно придумати схему їх тлумачення.
Найпростішим квадратним рівнянням, яке доставляє неприємності, є:
\[x^2 + 1 = 0 \label{A.3} \]
рішення, що є
\[x = \pm \sqrt{-1}\label{A.4} \]
Що це означає? Ми щойно бачили, що квадрат позитивного числа є позитивним, а квадрат негативного числа також позитивний, оскільки множення одного негативного числа, яке вказує назад, на інший, який перетворює будь-який вектор через 180 градусів, дає позитивний вектор. Інший спосіб сказати те ж саме - розглядати сам знак мінус, -, як оператор, який повертає число, до якого він застосовується через 180 градусів. Тепер в ньому\((-2)\times (-2)\) є два таких обертання, що дають повні 360 градусів назад до позитивної осі.
Щоб зрозуміти квадратний корінь негативного числа, нам потрібно знайти те, що при множенні на себе дає негативне число. Давайте сконцентруємося на даний момент на квадратному корені —1, з квадратного рівняння вище. Подумайте про —1 як оператор, який діє на вектор 1, тому — повертає вектор на 180 градусів. Нам потрібно знайти квадратний корінь цього оператора, оператор якого застосовується двічі, дає обертання на 180 градусів. Поставте так, це досить очевидно, що оператор, який ми хочемо, обертає вектор від 1 до 90 градусів.
Але якщо ми візьмемо позитивне число, наприклад, 1, і повернути його вектор через 90 градусів тільки, це не число взагалі, принаймні в нашому первісному сенсі, так як ми покласти всі відомі числа на одному рядку, і ми тепер повернувся 1 від цієї лінії. Нове число, створене таким чином, називається чистим уявним числом, і позначається символом\(i\).
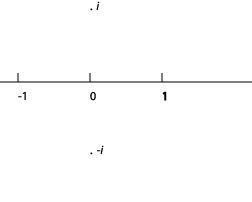
Після того, як ми знайшли квадратний корінь —1, ми можемо використовувати його, щоб записати квадратний корінь будь-якого іншого від'ємного числа - наприклад,\(2i\) квадратний корінь\(–4\). Складання дійсного числа з вихідного рядка з уявним числом (кратним i) дає комплексне число. Очевидно, комплексні числа заповнюють всю двовимірну площину. Беручи звичайні декартові координати, будь-яка точка\(P\) на площині може бути записана як\((x, y)\) де точка досягається від початку, йдучи\(x\) одиниць у напрямку позитивної дійсної осі, то y одиниць у напрямку\(i\), визначеному, іншими словами, \(y\) вісь.
Таким чином, точку P з координатами (x, y) можна ідентифікувати комплексним числом z, де
\[z = x + iy. \label{A.5} \]
Площину часто називають комплексною площиною, і представлення комплексних чисел таким чином іноді називають діаграмою Арганда.
Візуалізуючи комплексні числа як двовимірні вектори, зрозуміло, як скласти два з них разом. Якщо z 1 = х 1 + ii 1, а z 2 = х 2 + iy 2, то z 1 + z 2 = (х 1 + х 2) + i (у 1 + у 2). Реальні частини та уявні частини додаються окремо, так само, як і векторні компоненти.
Множення двох комплексних чисел разом не має зовсім такої простої інтерпретації. Це, однак, досить просто - застосовуються звичайні алгебраїчні правила, при цьому i 2 замінено там, де воно з'являється на - 1. Так, наприклад, помножити z 1 = х 1 + iy 1 на z 2 = х 2 + iy 2,
\[z_1z_2 = (x_1 + iy_1)( x_2 + iy_2) = (x_1x_2 - y_1y_2) + i(x_1y_2 + x_2y_1). \label{A.6} \]
Полярні координати
Деякі властивості комплексних чисел найлегше зрозуміти, якщо вони представлені за допомогою полярних координат\(r, \theta\) замість знаходження\((x, y)\)\(z\) в комплексній площині.
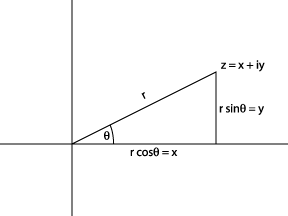
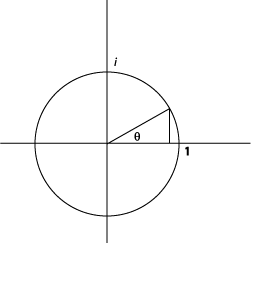
Зверніть увагу, що\(z = x + iy\) можна записати\(r(\cos \theta + i \sin \theta)\) з наведеної вище схеми. Насправді це уявлення призводить до більш чіткої картини множення двох комплексних чисел:
\[\begin{align} z_1z_2 &= r_2 ( \cos(\theta_1 + i\sin \theta_1) r_2( \cos(\theta_2 + i\sin \theta_2) \label{A.7} \\[4pt] & = r_1r_2 \left[ (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2) \right] \label{A.8} \\[4pt] & = r_1r_2 \left[ \cos(\theta_1+\theta_2) + i\sin (\theta_1+\theta_2) \right] \label{A.9} \end{align} \]
Отже, якщо
\[ z = r(cos \theta + i\sin \theta ) = z_1z_2 \label{A.10} \]
потім
\[r = r_1r_2 \label{A.11} \]
і
\[\theta=\theta_1\theta_2 \label{A.12} \]
Тобто, щоб помножити разом два комплексні числа, ми множимо r - звані модулі - і додаємо фази, ті. Модуль\(r\) часто позначається\(|z|\) і називається мод z, фаза\(\theta\) \(\theta\)іноді називають arg z. Наприклад\(|i| = 1\),\(\text{arg}\; i = \pi/2\).
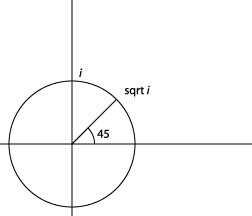
Тепер ми бачимо, що, хоча нам довелося ввести ці комплексні числа, щоб мати a\(\sqrt{-1}\), нам не потрібно вводити нові типи чисел, щоб отримати\(\sqrt{-1}\), або\(\sqrt{i}\). Зрозуміло\(|\sqrt{i}|=1\),,\( arg \sqrt{i} = 45°\). Він знаходиться на окружності одиниці радіусу по центру у початку координат, під 45 °, а квадрат його просто подвоює кут.
Одиничне коло
Насправді це коло, яке називається одиничним колом - відіграє важливу роль у теорії комплексних чисел, і кожна точка на колі має форму.
\[ z = \cos \theta + i \sin \theta = Cis(\theta) \label{A.13} \]
Оскільки всі точки на одиничному колі мають\(|z| = 1\), за визначенням, множення будь-яких двох з них разом просто означає додавання кутів, тому наша нова функція\(Cis(\theta)\) задовольняє
\[ Cis(\theta_1)Cis(\theta_2)=Cis(\theta_1+\theta_2). \label{A.14} \]
Але це саме те, як множення працює для експонентів! Тобто,
\[a^{\theta_1}a^{\theta_2} = a^{\theta_1+\theta_2} \label{A.15} \]
для\(a\) будь-якої константи, яка настійно говорить про те, що, можливо, наша функція\(Cis(\theta\) не що інше, як якась постійна\(a\) піднята до влади\(\theta\), тобто
\[ Cis(\theta) = a^{\theta}\label{A.16} \]
Виходить зручно писати\(a^{\theta} = e^{(\ln a)\theta} = e^{A \theta}\), де\(A = \ln a\). Цей рядок міркувань змушує нас писати
\[\cos \theta + i\sin \theta = e^{A\theta} \label{A.17} \]
Тепер, щоб вищевказана «формула додавання» працювала на множення,\(A\) повинна бути постійною, незалежною від\(\theta\). Тому ми можемо знайти значення А, вибираючи,\(\theta\) для яких речей прості. Ми беремо\(\theta\), щоб бути дуже малим - в цьому обмеженні:
\[ \cos \theta = 1 \nonumber \]
\[ \sin \theta = \theta \nonumber \]
\[ e^{A\theta} = 1+ A\theta \nonumber \]
з ми скидаємо умови замовлення\(\theta^2\) і вище.
Підстановка цих значень у рівняння\ ref {A.17} дає\(\theta\)
Так ми знаходимо:
\[ (\cos \theta + i \sin \theta) e ^{i \theta} \label{A.18} \]
Щоб перевірити цей результат, розгортаємо\(e^{i \theta}\):
\[ \begin{align} e^{i \theta} &= 1 + i\theta + \dfrac{(i\theta)^2}{2!} + \dfrac{(i\theta)^3}{3!} + \dfrac{(i\theta)^4}{4!} + \dfrac{(i\theta)^5}{5!} ... \label{A.19a} \\[4pt] &= 1 + i\theta - \dfrac{\theta^2}{2!} - \dfrac{i\theta^3}{3!} +\dfrac{\theta^4}{4!} +\dfrac{i\theta^5}{5!} ... \label{A.19b} \\[4pt] &= \left( 1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} \right) + i \left(\theta - \dfrac{i\theta^3}{3!}+\dfrac{i\theta^5}{5!} \right) \label{A.19c} \\[4pt] &= \cos \theta + i\sin \theta \label{A.19d} \end{align} \]
Ми пишемо\(= \cos \theta + i\sin \theta\) в Equation\ ref {a.19d}, оскільки ряди в дужках є саме рядами Тейлора для\(\cos \theta\) і\(\sin \theta\) підтверджують наше рівняння для\(e^{i\theta}\). Змінюючи знак\(\theta\), легко помітити, що
\[ e^{-i \theta} = \cos \theta - i\sin \theta \label{A.20} \]
так дві тригонометричні функції можуть бути виражені через експоненціальні числа комплексних чисел:
\[\cos (\theta) = \dfrac{1}{2} \left( e^{i\theta} + e^{-i \theta} \right) \nonumber \]
\[\sin (\theta) = \dfrac{1}{2i} \left( e^{i\theta} - e^{-i \theta} \right) \nonumber \]
Формула Ейлера стверджує, що будь-яке комплексне число може бути записано:
\[e^{i \theta} = \cos \theta + i\sin \theta \nonumber \]