9.8: Кислотно-лужні рівноваги
- Page ID
- 21007
Дуже багато процесів передбачають перенесення протонів, або кислотно-лужних типів реакцій. Оскільки багато біологічних систем залежать від ретельно контрольованого рН, ці типи процесів надзвичайно важливі. Показник рН визначається
\[ pH \equiv -\log a(\ce{H^{+}}) \approx -\log [\ce{H^{+}}] \label{eq1}\]
де\(a\) - активність іонів гідронію і\([\ce{H^{+}}]\) справжня концентрація іонів гідронію (як в моль/л).
Дисоціація слабкої кислоти у воді регулюється рівновагою, визначеною
\[HA(aq) \rightleftharpoons H^+(aq) + A^-(aq)\]
Постійна рівноваги для такої реакції\(K_a\),, приймає форму
\[K_a = \dfrac{[H^+][A^-]}{[HA]} \label{eq3}\]
Як і у випадку з усіма термодинамічними константами рівноваги, концентрації замінюються діяльністю, а постійна рівноваги безроздільна. Однак, якщо всі види ведуть себе ідеально (мають коефіцієнти одиничної активності), одиниці можуть бути використані як дуже корисний посібник при вирішенні завдань.
Приклад\(\PageIndex{1}\): Acetic Acid
Що таке рН 0,200 М розчину HoAc (оцтової кислоти)? (К а = 1,8 х 10 -5 М)
Рішення:
Тут дуже до речі стане в нагоді стіл ICE!
| \([HOAc]\) | \([H^+]\) | \([OAc^-]\) | |
|---|---|---|---|
| I початковий | \ ([HoAC]\) ">0,200 М | \ ([H^+]\) ">0 | \ ([ОАС ^-]\) ">0 |
| C Зміна | \ ([HoAC]\) ">-x | \ ([H ^ +]\) ">+х | \ ([ОАС ^-]\) ">+х |
| E рівновага | \ ([HoAC]\) ">0,200 М - х | \ ([H ^ +]\) ">х | \ ([ОАС ^-]\) ">х |
Потім проблему рівноваги можна встановити як
\[ K_a = \dfrac{[H^+][OAc^-]}{[HOAc]}\]
Підстановка значень, які відомі
\[ 1.8 \times 10^{-5} =\dfrac{ x^2}{0.200 \, M -x}\]
Це дає квадратне рівняння, і, таким чином, два значення\(x\) яких задовольняють співвідношення.
\[x_1 = -0.001906 \,M\]
\[x_2 = 0.001888 \,M\]
Негативний корінь фізично не має сенсу, оскільки концентрації\(H^+\) і\(OAc^-\) не можуть бути негативними. Використовуючи значення\(x_2\) as\([H^+]\), pH потім обчислюється (через Equation\ ref {eq1}), щоб бути
\[ pH \approx -\log_{10} (0.001888) = 2.72\]
Автоіонізація води
Вода є дуже важливим розчинником, оскільки молекули води мають великі дипольні моменти, які створюють сприятливі взаємодії з іонними сполуками. Вода також має велику діелектричну проникність, яка гасіння електричного поля, що генерується іонами в розчині, роблячи порівняльні взаємодії з водою більш сприятливими, ніж з іншими іонами в розчині у багатьох випадках. Але вода також дисоціює на іони через реакцію
\[H_2O(l) \rightleftharpoons H^+(aq) + OH^-(aq) \label{eqA}\]
Константа рівноваги, що регулює цю дисоціацію, сильно залежить від температури. Дані нижче представлені Бандурою та Львовом (Bandura & Lviv, 2006)
| Т (°C) | 0 | 25 | 50 | 75 | 100 |
|---|---|---|---|---|---|
| пК ш | 14,95 | 13,99 | 13.26 | 12.70 | 12.25 |
З цих даних можна побудувати ділянку фургона Гоффа.
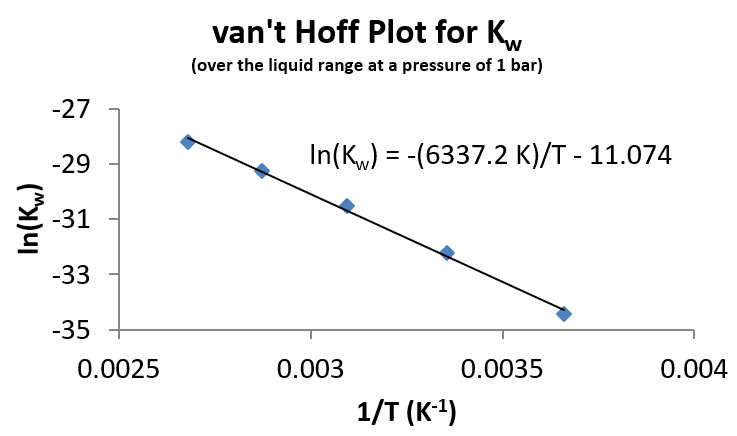
Існує певна кривизна лінії, що свідчить про деяку (хоча і малу) залежність температури\(\Delta H_{rxn}\) для рівняння\ ref {eQa}. Однак з підгонки цих даних значення\(\Delta H_{rxn}\) може бути визначено рівним 52,7 кДж/моль. Особливо слід зазначити, що дисоціація носить ендотермічний характер, тому підвищення температури призведе до більшого ступеня дисоціації.
Приклад\(\PageIndex{2}\): Neutral Water
Який рН нейтральної води при 37° C (нормальна температура тіла людини)? Нейтральна вода без надлишку\([OH^-]\) або навпаки.\([H^+]\)
Рішення:
З найбільш підходящої лінії на графіку Ван Гоффа Figure\(\PageIndex{1}\)\(K_w\) можна обчислити значення:
\[ \ln (K_w) = - \dfrac{6338 \,K}{310\,K} - 11.04\]
\[ K_w= 2.12 \times 10^{-14}\,M^2\]
Так як\(K_w\) дає продукт\([H^+]\) і\([OH^-]\) (який повинен бути рівним в нейтральному розчині),
\[H^+] = \sqrt{2.12 \times 10^{-14}\,M^2} = 1.456 \times 10^{-7}\,M\]
А рН задається (Рівняння\ ref {eq1}):
\[ pH = -\log_{10} (1.456 \times 10^{-7}) = 6.84\]
Примітка: Це трохи менше, ніж рН 7,00, який зазвичай вважається «нейтральним». Але рН 7,00 є нейтральним лише при 25° C! При більш високих температурах нейтральний рН є меншим значенням через ендотермічну природу води з автоіонізацією. Хоча він має вищу\([H^+]\) концентрацію, він також має вищий\([OH^-]\) і на тому ж рівні, тому він все ще технічно нейтральний.
Гідроліз слабкої основи
Гідроліз визначається як реакція з водою, яка розщеплює молекулу води. Гідроліз слабкої основи визначає постійну рівноваги K b.
\[A^- + H_2O \rightleftharpoons HA + OH^-\]
Для цієї реакції константа рівноваги\(K_b\) задається
\[ K_b = \dfrac{[HA][OH^-]}{[A^-]} \]
Концентрація (або активність) чистої сполуки H 2 O не включається в вираз рівноваги, оскільки, будучи чистою сполукою в стандартному стані, вона має одиничну активність протягом усього процесу встановлення рівноваги. Далі слід зазначити, що коли K b поєднується з виразом для K a для слабкої кислоти HA (Equation\ ref {eq3}),
\[K_a K_b = \left( \dfrac{[H^+][A^-]}{[HA]} \right) \left( \dfrac{[HA][OH^-]}{[A^-]} \right) = [H^+][OH^-] = K_w \]
Як наслідок, якщо хтось знає\(K_a\) слабку кислоту, він також знає\(K_b\) її кон'югатну основу, оскільки продукт призводить до\(K_w\).
Приклад\(\PageIndex{3}\):
Що таке рН 0,150 М розчину КФ? (Для ВЧ, рК а = 3,17 при 25° C)
Рішення:
Проблема пов'язана з гідролізом кон'югатного підстави HF, F -. Реакція гідролізу
\[F^- + H_2O \rightleftharpoons HF + OH^-\]
Стіл ICE тут в порядку.
| \(F^-\) | \(HF\) | \(OH^-\) | |
|---|---|---|---|
| I початковий | \ (F^-\) ">0,150 М | \ (HF\) ">0 | \ (ОХ ^-\) ">0 |
| C Зміна | \ (F^-\) ">-х | \ (ВЧ\) ">+х | \ (ОХ^-\) ">+х |
| E рівновага | \ (F^-\) ">0,150 М - х | \ (ВЧ\) ">х | \ (ОХ^-\) ">х |
Отже, вираз\(K_b\) для
\[ K_b = \dfrac{K_w}{K_a} = \dfrac{1.0 \times 10^{-14} M^2}{10^{3.17} M} = \dfrac{x^2}{1.50 \,M-x}\]
При цьому мале значення\(K_b\) страхує, що значення х буде мізерно малим в порівнянні з 0,150 М. У цій межі значення\(x\) (яке дорівнює [ОН -])
\[ x = [OH^-] = 1.49 \times 10^{-6}\,M\]
\([H^+]\)Так дається
\[ [H^+] =\dfrac{K_w}{[OH^-]} = \dfrac{10^{-14} M^2}{1.49 \times 10^{-6} M} = 6.71 \times 10^{-9} \,M\]
А рН задається (Рівняння\ ref {eq1}):
\[ pH = -\log_{10} (6.71 \times 10^{-9}) = 8.17\]
Примітка: рН цього сольового розчину трохи основний. Цього слід очікувати, оскільки KF можна вважати, що утворюється в реакції слабкої кислоти (HF) з сильною основою (КОН). У змаганні за контроль рН сильна база закінчується перемогою битви.
