Skip to main content
LibreTexts - Ukrayinska

1.18: Склеювання в діатоміці

  1. Last updated
  2. Save as PDF
  • Page ID
    17607

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

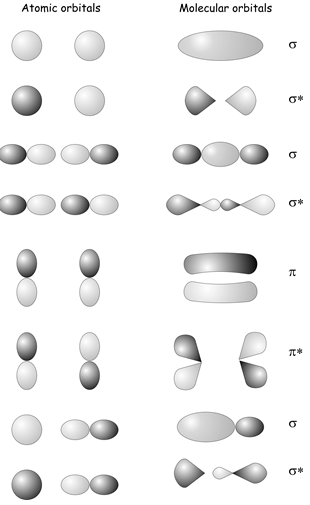    альтВи вже будете знайомі з ідеєю побудови молекулярних орбіталів з лінійних комбінацій атомних орбіталів з попередніх курсів, що охоплюють зв'язок у двоатомних молекулах. Розглядаючи симетрії\(s\) and \(p\) orbitals on two atoms, we can form bonding and antibonding combinations labeled as having either \(\sigma\) або\(\pi\) симетрію залежно від того, чи нагадують вони\(s\) or \(p\) orbitals when viewed along the bond axis (see diagram below). In all of the cases shown, only atomic orbitals that have the same symmetry when viewed along the bond вісь\(z\) can form a chemical bond e.g. two \(s\) orbitals, two \(p_z\) orbitals , or an \(s\) and a \(p_z\) can form a bond, but a \(p_z\) and a \(p_x\) or an \(s\) and a \(p_x\) or a \(p_y\) cannot. It turns out that the rule that determines whether or not two atomic orbitals can bond is that they must belong to the same symmetry species within the point group of the molecule.

    Ми можемо довести це математично для двох атомних орбіталів\(\phi_i\) і, дивлячись\(\phi_j\) на інтеграл перекриття між двома орбіталями.

    \[S_{ij} = \langle \phi_i|\phi_j \rangle = \int \phi_i^* \phi_j d\tau \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \text(18.1)\]

    Для того щоб скріплення було можливим, цей інтеграл повинен бути ненульовим. Добуток двох функцій\(\phi_1\) і\(\phi_2\) перетворюється як прямий добуток їх симетрії виду тобто\(\Gamma_{12}\) =\(\Gamma_1 \otimes \Gamma_2\). Як пояснювалося вище, для того, щоб інтеграл перекриття був ненульовим,\(\Gamma_{12}\) повинен містити повністю симетричне нескорочуване подання (\(A_{1g}\) for a homonuclear diatomic, which belongs to the point group \(D_{\infty h}\)). As it happens, this is only possible if \(\phi_1\)і\(\phi_2\) належати до того ж нескорочуваного представництво. Ці ідеї зведені для двоатомного в таблиці нижче.

    \[\begin{array}{lllll} \hline \text{First Atomic Orbital} & \text{Second Atomic Orbital} & \Gamma_1 \otimes \Gamma_2 & \text{Overlap Integral} & \text{Bonding?} \\ \hline s \: (A_{1g}) & s \: (A_{1g}) & A_{1g} & \text{Non-zero} & \text{Yes} \\ s \: (A_{1g}) & p_x \: (E_{1u}) & E_{1u} & \text{Zero} & \text{No} \\ s \: (A_{1g}) & p_z \: (A_{1u}) & A_{1u} & \text{Zero} & \text{No} \\ p_x \: (E_{1u}) & p_x \: (E_{1u}) & A_{1g} + A_{2g} + E_{2g} & \text{Non-zero} & \text{Yes} \\ p_X \: (E_{1u}) & p_z \: (A_{1u}) & E_{1g} & \text{Zero} & \text{No} \\ p_z \: (A_{1u}) & p_z \: (A_{1u}) & A_{1g} & \text{Non-zero} & \text{Yes} \end{array} \tag{18.2}\]