17.4: Рівняння Нернста

Last updated
Save as PDF

Page ID: 22473

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Пов'язати потенціали клітин до змін вільної енергії
Використовуйте рівняння Нернста для визначення потенціалів клітин в нестандартних умовах
Виконуйте розрахунки, які передбачають перетворення між потенціалами клітин, зміни вільної енергії та константи рівноваги

Тепер ми продовжимо електрохімію, визначивши взаємозв'язок між\(E^\circ_\ce{cell}\) і термодинамічними величинами, такими як Δ G° (вільна енергія Гіббса) і K (постійна рівноваги). У гальванічних елементах хімічна енергія перетворюється в електричну енергію, яка може виконувати роботу. Електромонтажні роботи - це твір переданого заряду, помножене на різницю потенціалів (напруга):

\[\mathrm{electrical\: work=volts \times (charge\: in\: coulombs)=J} \nonumber \]

Заряд на 1 моль електронів задається постійною Фарадея (F)

\[ \begin{align*} F &=\dfrac{6.022 \times 10^{23}\:e^-}{mol} \times \dfrac{1.602 \times 10^{−19}\:C}{e^-} \\[4pt] &=9.648 \times 10^4\:\dfrac{C}{mol} \\[4pt] &=9.648 \times 10^4\:\dfrac{J}{V⋅mol} \end{align*} \nonumber \]

Тому

\[\mathrm{total\: charge=(number\: of\: moles\: of\: e^-)} \times F=nF \nonumber \]

У цьому рівнянні\(n\) вказується кількість молів електронів для збалансованої окислювально-відновної реакції. Виміряний потенціал комірки - це максимальний потенціал, який може виробляти комірка, і пов'язаний з електромонтажними роботами (w _ele)

\[E_\ce{cell}=\dfrac{−w_\ce{ele}}{nF}\hspace{40px}\ce{or}\hspace{40px}w_\ce{ele}=−nFE_\ce{cell} \nonumber \]

Негативний знак для роботи говорить про те, що електромонтажні роботи виконуються системою (гальванічним елементом) на оточення. У попередньому розділі вільна енергія була визначена як енергія, яка була доступна для роботи. Зокрема, зміна вільної енергії було визначено з точки зору максимальної роботи (\(w_{max}\)), яка, для електрохімічних систем, є\(w_{ele}\).

\[\begin{align*} ΔG&=w_\ce{max}=w_\ce{ele} \\[4pt] &=−nFE_\ce{cell} \end{align*} \nonumber \]

Ми можемо перевірити, що ознаки правильні, коли усвідомлюємо, що\(n\) і\(F\) є позитивними константами і що гальванічні елементи, які мають позитивні потенціали клітин, включають спонтанні реакції. Таким чином, спонтанні реакції, які мають\(ΔG < 0\), повинні мати\(E_{cell} > 0\). Якщо всі реагенти і продукти знаходяться в своїх стандартних станах, це стає

\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]

Це забезпечує спосіб співвідносити стандартні потенціали клітин з константами рівноваги, оскільки

\[ΔG°=−RT\ln K \nonumber \]

\[−nFE^\circ_\ce{cell}=−RT\ln K \nonumber \]

або

\[ E^\circ_\ce{cell}=\dfrac{RT}{nF}\ln K \nonumber \]

Більшу частину часу електрохімічні реакції протікають при стандартній температурі (298,15 К). Терміни збору при цій температурі дають

\[\begin{align*} E^\circ_\ce{cell}&=\dfrac{RT}{nF}\:\ln K \\[4pt] &=\dfrac{\left(8.314\:\dfrac{\ce{J}}{\textrm{K⋅mol}}\right)(298.15\:K)}{n \times 96,485\: \textrm{C/V⋅mol}}\:\ln K \\[4pt] &=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K \end{align*} \nonumber \]

де\(n\) - кількість молів електронів. Логарифм у рівняннях, що включають потенціали клітин, часто виражається за допомогою логарифмів основи 10 (тобто\(\log_{10}\) або просто\(\log\)), що змінює константу в 2,303 рази:

\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]

Таким чином, якщо Δ G°, K, або\(E^\circ_\ce{cell}\) відомо або може бути обчислене, інші дві величини можуть бути легко визначені. Відносини зображені графічно на малюнку\(\PageIndex{1}\).

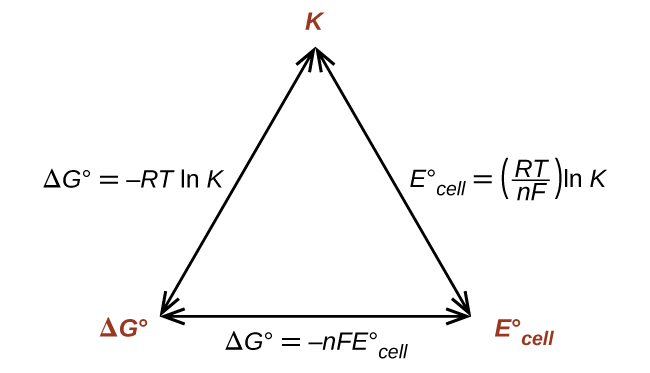
Малюнок\(\PageIndex{1}\): Відносини між ΔG°, K і *\(E^\circ_\ce{cell}\).* Враховуючи будь-яку з трьох величин, інші дві можна обчислити, тому будь-яка з величин може бути використана для визначення того, чи був процес спонтанним.

З огляду на будь-яку одну з величин, можна обчислити дві інші.

Приклад\(\PageIndex{1}\): Equilibrium Constants, Potentials, & Free Energy Changes

Що таке стандартна зміна вільної енергії Гіббса та постійна рівноваги для наступної реакції при 25° C?

\[\ce{2Ag+}(aq)+\ce{Fe}(s)⇌\ce{2Ag}(s)+\ce{Fe^2+}(aq) \nonumber \]

Отже, розрідження

Реакція передбачає окислювально-відновну реакцію, тому стандартний потенціал клітини можна розрахувати, використовуючи дані таблиці Р1.

\ [\ почати {вирівнювати*}
&\ textrm {анод (окислення):}\ ce {Fe} (s) ⟶\ ce {Fe^2+} (aq) +\ ce {2e-}\ hspace {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0.447\: V}\ nonumber\
&\ textrm {катод (зменшення):} 2\ раз (\ ce {Ag+} (q) +\ ce {e-} ⟶\ ce {Ag} (s))\ hspace {40px} E^\ circ_ {\ ce {Ag+/Ag}} =\ mathrm {0.7996\ : V}\ номер\\
&E^\ circ_\ ce {комірка} =Е^\ circ_\ ce {катод} −E^\ circ_\ ce {анод} =Е^\ circ_ {\ ce {Ag+/Ag}} −E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {+1.247\ V:}\ nonumber
\ end {вирівнювати*}\ nonumber\]

Пам'ятайте, що потенціал осередку для катода не множиться на два при визначенні стандартного потенціалу осередку. При n = 2 константа рівноваги тоді

\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]

\[\begin{align*} K&=10^{n \times E^\circ_\ce{cell}/\mathrm{0.0592\: V}} \\[4pt] &=10^{2 \times \mathrm{1.247\: V/0.0592\: V}} \\[4pt] &=10^{42.128} \\[4pt] &=1.3 \times 10^{42}\end{align*} \nonumber \]

Стандартна вільна енергія тоді

\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]

\[ΔG°=\mathrm{−2 \times 96,485\:\dfrac{J}{\textrm{V⋅mol}} \times 1.247\: V=−240.6\:\dfrac{kJ}{mol}} \nonumber \]

Перевірте свою відповідь: Позитивний стандартний потенціал клітини означає спонтанну реакцію, тому стандартна зміна вільної енергії повинна бути негативною, а постійна рівноваги повинна бути >1.

Вправа\(\PageIndex{1}\)

Що таке стандартна зміна вільної енергії Гіббса і постійна рівноваги для наступної реакції при кімнатній температурі? Чи є реакція спонтанною?

\[\ce{Sn}(s)+\ce{2Cu^2+}(aq)⇌\ce{Sn^2+}(aq)+\ce{2Cu+}(aq) \nonumber \]

Відповідь: Спонтанний; n = 2\(E^\circ_\ce{cell}=\mathrm{+0.291\: V}\);\(ΔG°=\mathrm{−56.2\:\dfrac{kJ}{mol}}\);;\(K = 6.8 \times 10^9\).

Тепер, коли встановлено зв'язок між вільною енергією та потенціалами клітин, слідують нестандартні концентрації. Нагадаємо, що

\[ΔG=ΔG°+RT\ln Q \nonumber \]

де\(Q\) - коефіцієнт реакції (див. Розділ про основи рівноваги). Перетворення в потенціали клітин:

\[−nFE_\ce{cell}=−nFE^\circ_\ce{cell}+RT\ln Q \label{nernst1A} \]

або

\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \label{nernst1B} \]

Рівняння\ ref {NernSt1b} - узагальнене рівняння Нернста, яке застосовується при будь-якій температурі. Однак його можна спростити для реакцій, що відбуваються при 25° C (298,15 K), переписуючи його як

\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0257\: V}}{n}\:\ln Q \label{nernst2A} \]

або

\[ E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\log_{10} Q \label{nernst2B} \]

Якщо температура не дорівнює 298,15 К, необхідно перерахувати потенціал за допомогою Equation\ ref {NernSt1b}. За допомогою рівняння Нернста можна обчислити потенціал клітини в нестандартних умовах. Це коригування необхідно, оскільки потенціали, визначені в різних умовах, матимуть різні значення.

Приклад\(\PageIndex{2}\): Cell Potentials at Nonstandard Conditions

Розглянемо наступну реакцію при кімнатній температурі:

\[\ce{Co}(s)+\ce{Fe^2+}(aq,\:1.94\:M)⟶\ce{Co^2+}(aq,\: 0.15\:M)+\ce{Fe}(s) \nonumber \]

Чи є процес спонтанним?

Рішення

Існує два шляхи вирішення проблеми. Якби термодинамічна інформація в таблиці Т1 була доступна, можна було б обчислити зміну вільної енергії. Якщо зміна вільної енергії негативна, процес відбувається спонтанно. Інший підхід, який ми будемо використовувати, вимагає інформації, подібної до наведеної в таблиці P1. Використовуючи ці дані, можна визначити потенціал клітини. Якщо потенціал клітини позитивний, процес спонтанний. Збір інформації з таблиці Р1 і проблеми,

\ [\ почати {вирівнювати*}
&\ textrm {Анод (окислення):}\ ce {Co} (s) ⟶\ ce {Co^2+} (q) +\ ce {2e-}\ hspace {40px} E^\ circ_ {\ ce {Co^2+/Co}} =\ mathrm {−0.28\: V}\\
&\ textrm {Катод (зменшення):}\ ce {Fe^2+} (aq) +\ ce {2e-} ⟶\ ce {Fe} (s)\ hпростір {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0.447\: V}\\
&E^\ circ_\ ce {осередок} =E^\ circ_\ ce {катод} −E^\ circ_\ ce {анод} =\ матхрм {−0,447\: V) = −0.28\: V}
\ кінець {вирівнювати*}\ номер\]

Процес не є спонтанним при стандартних умовах. Використовуючи рівняння Нернста та концентрації, зазначені в задачі і\(n = 2\),

\[Q=\ce{\dfrac{[Co^2+]}{[Fe^2+]}}=\dfrac{0.15\:M}{1.94\:M}=0.077 \nonumber \]

Тепер ми можемо вставити їх у рівняння Нернста при кімнатній температурі (Equation\ ref {NernSt2b})

\[\begin{align*} E_\ce{cell} &=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \\[4pt] &=\mathrm{−0.17\: V−\dfrac{0.0592\: V}{2}\:\log 0.077} \\[4pt] &=\mathrm{−0.17\: V+0.033\: V=−0.14\: V} \end{align*} \nonumber \]

Процес є (досі) неспонтанним.

Вправа\(\PageIndex{2}\)

Який потенціал клітини для наступної реакції при кімнатній температурі?

\[\ce{Al}(s)│\ce{Al^3+}(aq,\:0.15\:M)║\ce{Cu^2+}(aq,\:0.025\:M)│\ce{Cu}(s) \nonumber \]

Які значення n і Q для загальної реакції? Чи спонтанна реакція в цих умовах?

Відповідь: n = 6; Q = 1440; E _{клітина} = +1,97 В, спонтанна.

Нарешті, ми коротко розглянемо особливий тип клітини, який називається концентраційною клітиною. У концентраційній комірці електроди - це один і той же матеріал, а напівклітини відрізняються лише концентрацією. Оскільки один або обидва відсіки не є стандартними, потенціали клітин будуть нерівні; отже, буде різниця потенціалів, яку можна визначити за допомогою рівняння Нернста.

Приклад\(\PageIndex{3}\): Concentration Cells

Який клітинний потенціал концентраційної клітини описується

\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\: 0.10\:M)║\ce{Zn^2+}(aq,\: 0.50\:M)│\ce{Zn}(s) \nonumber \]

Отже, розрідження

З наданої інформації:

\ [\ почати {вирівнювати*}
&\ textrm {Анод:}\ ce {Zn} (s) ⟶\ ce {Zn^2+} (aq,\: 0.10\ :M) +\ ce {2e-}\ hspace {40px} E^\ circ_\ ce {анод} =\ mathrm {−0.7618\: V}\\
&\ textrm {Катод де:}\ ce {Zn ^ 2+} (aq,\: 0.50\ :M) +\ ce {2e-} ⟶\ ce {Zn} (s)\ hspace {40px} E^\ circ_\ ce {катод} =\ mathrm {−0.7618\: V}\\
& підсилювач;\ верхня лінія {\ textrm {Загальний:}\ ce {Zn^2+} (q,\: 0.50\ :M) ⟶\ ce {Zn^2+} (q,\: 0.10\ :M)\ hspace {40px} E^\ circ_\ ce {комірка} =\ mathrm {0.000\ V}}
\ кінець {align*}\ nonumber\]

Стандартний потенціал комірки дорівнює нулю, оскільки анод і катод включають однакову реакцію; змінюється лише концентрація Zn ² ⁺. Підставляючи в рівняння Нернста,

\[E_\ce{cell}=\mathrm{0.000\: V−\dfrac{0.0592\: V}{2}\:\log\dfrac{0.10}{0.50}=+0.021\: V} \nonumber \]

і процес відбувається спонтанно при цих умовах.

Перевірте свою відповідь: У концентраційній комірці стандартний потенціал клітини завжди дорівнюватиме нулю. Для отримання позитивного потенціалу клітини (спонтанний процес) коефіцієнт реакції Q повинен бути <1. Q < 1 в даному випадку, тому процес є спонтанним.

Вправа\(\PageIndex{3}\)

Яке значення Q для попередньої концентраційної комірки призведе до напруги 0,10 В? Якщо концентрація іона цинку на катоді становила 0,50 М, яка була концентрація на аноді?

Відповідь: Q = 0.00042; [Zn ² ⁺] _кішка = 2,1\ раз 10 ⁻⁴ М.

Резюме

Електромонтажні роботи (w _ele) - це негатив добутку сумарного заряду (Q) і потенціалу клітини (Е _{осередок}). Загальний заряд можна обчислити як кількість молів електронів (n), що перевищує константу Фарадея (F = 96 485 C/моль e ⁻). Електромонтажні роботи - це максимальна робота, яку може виробляти система і так дорівнює зміні вільної енергії. Таким чином, все, що можна зробити з або до вільної зміни енергії, також може бути зроблено з потенціалом клітини або з ним. Рівняння Нернста пов'язує потенціал клітини в нестандартних умовах з логарифмом частки реакції. Концентраційні клітини експлуатують цей зв'язок і виробляють позитивний потенціал клітини, використовуючи напівклітини, які відрізняються лише концентрацією їх розчинених речовин.

Ключові рівняння

\(E^\circ_\ce{cell}=\dfrac{RT}{nF}\:\ln K\)
\(E^\circ_\ce{cell}=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
\(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \hspace{40px} \textrm{(Nernst equation)}\)
\(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathit{0.0257\: V}}{n}\:\ln Q=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
Δ G = − _{клітина} NFe
\(ΔG^∘=−nFE^\circ_\ce{cell}\)
\(w_\ce{ele}=w_\ce{max}=−nFE_\ce{cell}\)

Глосарій

концентрація клітини: гальванічний елемент, в якому два півклітини однакові, за винятком концентрації розчинених речовин; спонтанний, коли загальна реакція - це розведення розчиненої речовини

електромонтажні роботи (з _еле): від'ємний від загального заряду, що умножує потенціал клітини; дорівнює w _max для системи, і так дорівнює зміні вільної енергії (Δ G)

Константа Фарадея (F): заряд на 1 моль електронів; F = 96,485 С/моль е ⁻

Рівняння Нернста: рівняння, яке пов'язує логарифм реакційного коефіцієнта (Q) з нестандартними потенціалами клітин; може бути використано для зв'язку констант рівноваги зі стандартними потенціалами клітин