9.3: Стехіометрія газоподібних речовин, сумішей та реакцій
- Page ID
- 22728
↑
- Використовуйте ідеальний закон газу для обчислення щільності газу та молярних мас
- Виконати стехіометричні розрахунки за участю газоподібних речовин
- Державний закон Далтона про парціальні тиски і використання його в розрахунках за участю газоподібних сумішей
Вивчення хімічної поведінки газів було частиною основи, мабуть, самої фундаментальної хімічної революції в історії. Французький дворянин Антуан Лавуазьє, який широко вважається «батьком сучасної хімії», змінив хімію з якісної на кількісну науку завдяки своїй роботі з газами. Він відкрив закон збереження речовини, відкрив роль кисню в реакціях горіння, визначив склад повітря, пояснив дихання з точки зору хімічних реакцій і багато іншого. Він став жертвою Французької революції, гільйотинованої в 1794 році. Про його смерть математик і астроном Жозеф Луї Лагранж сказав: «Мафії знадобилося лише мить, щоб зняти голову; століття не вистачить, щоб її відтворити».
Як описано в попередньому розділі цього тексту, ми можемо звернутися до хімічної стехіометрії для відповідей на багато питань, які задають «Скільки?» Відповісти на питання можна масами речовин або обсягами розчинів. Однак відповісти на це питання можна і іншим способом: з обсягами газів. Ми можемо використовувати ідеальне рівняння газу, щоб зв'язати тиск, об'єм, температуру та кількість молів газу. Тут ми об'єднаємо ідеальне рівняння газу з іншими рівняннями, щоб знайти щільність газу та молярну масу. Розберемося з сумішами різних газів, і розрахуємо кількість речовин в реакціях за участю газів. Цей розділ не представить жодного нового матеріалу чи ідей, але надасть приклади додатків та способи інтеграції концепцій, які ми вже обговорювали.
Щільність газу
Нагадаємо, що щільність газу - це його відношення маси до обсягу,\(ρ=\dfrac{m}{V}\). Тому, якщо ми зможемо визначити масу якогось об'єму газу, ми отримаємо його щільність. Щільність невідомого газу може використовуватися для визначення його молярної маси і тим самим допомогти в його ідентифікації. Ідеальний закон газу, PV = nRT, надає нам засіб отримання такої математичної формули, щоб пов'язати щільність газу з його об'ємом у доказі, показаному в прикладі\(\PageIndex{1}\).
Використовуйте PV = nRT, щоб отримати формулу для щільності газу в г/л
S рішення
\[PV = nRT \nonumber \]
Перевпорядкувати, щоб отримати (моль/л):
\[\dfrac{n}{v}=\dfrac{P}{RT} \nonumber \]
Помножте кожну сторону рівняння на молярну масу,. При розмноженні родимок на в г/моль отримують г:
\[(ℳ)\left(\dfrac{n}{V}\right)=\left(\dfrac{P}{RT}\right)(ℳ) \nonumber \]
\[ℳ/V=ρ=\dfrac{Pℳ}{RT} \nonumber \]
Було виявлено, що газ має щільність 0,0847 г/л при 17,0° C і тиск 760 торр. Яка його молярна маса? Що таке газ?
- Відповідь
-
\[ρ=\dfrac{Pℳ}{RT} \nonumber \]
\[\mathrm{0.0847\:g/L=760\cancel{torr}×\dfrac{1\cancel{atm}}{760\cancel{torr}}×\dfrac{\mathit{ℳ}}{0.0821\: L\cancel{atm}/mol\: K}×290\: K} \nonumber \]
= 2,02 г/моль; отже, газ повинен бути водень (Н 2, 2,02 г/моль)
Ми повинні вказати як температуру, так і тиск газу при розрахунку його щільності, оскільки кількість молів газу (і, отже, маса газу) в літрі змінюється з температурою або тиском. Щільність газу часто повідомляється в STP.
Використовуючи закон ідеального газу та щільність газового циклопропану, газ, який колись використовувався з киснем як загальний анестетик, складається з 85,7% вуглецю та 14,3% водню за масою. Знайдіть емпіричну формулу. Якщо 1,56 г циклопропану займає об'єм 1,00 л при 0,984 атм і 50° С, яка молекулярна формула циклопропану?
Рішення
Стратегія:
Спочатку вирішуйте емпіричну задачу формули за допомогою методів, розглянутих раніше. Припустімо 100 г і перетворюємо відсоток кожного елемента в грами. Визначити кількість молів вуглецю і водню в 100-г пробі циклопропану. Розділіть на найменшу кількість молів, щоб співвіднести кількість молів вуглецю до кількості молів водню. На останньому кроці зрозумійте, що найменшим цілим числовим співвідношенням є емпірична формула:
\[\mathrm{85.7\: g\: C×\dfrac{1\: mol\: C}{12.01\: g\: C}=7.136\: mol\: C\hspace{20px}\dfrac{7.136}{7.136}=1.00\: mol\: C} \nonumber \]
\[\mathrm{14.3\: g\: H×\dfrac{1\: mol\: H}{1.01\: g\: H}=14.158\: mol\: H\hspace{20px}\dfrac{14.158}{7.136}=1.98\: mol\: H} \nonumber \]
Емпірична формула - СН 2 [емпірична маса (ЕМ) 14,03 г/емпірична одиниця].
Далі використовуйте рівняння щільності, пов'язане із законом ідеального газу, для визначення молярної маси:
\[d=\dfrac{Pℳ}{RT}\hspace{20px}\mathrm{\dfrac{1.56\: g}{1.00\: L}=0.984\: atm×\dfrac{ℳ}{0.0821\: L\: atm/mol\: K}×323\: K} \nonumber \]
= 42,0 г/моль\(\dfrac{ℳ}{Eℳ}=\dfrac{42.0}{14.03}=2.99\), так (3) (СН 2) = C 3 H 6 (молекулярна формула)
Ацетилен - паливо, яке використовується зварювальними пальниками, складається з 92,3% С і 7,7% Н по масі. Знайдіть емпіричну формулу. Якщо 1,10 г ацетилену займає об'єм 1,00 л при 1,15 атм і 59,5 °С, яка молекулярна формула ацетилену?
- Відповідь
-
Емпірична формула, CH; Молекулярна формула, C 2 H 2
Молярна маса газу
Ще одне корисне застосування закону ідеального газу передбачає визначення молярної маси. За визначенням, молярна маса речовини - це відношення його маси в грамах, м, до його кількості в молі, n:
\[ℳ=\mathrm{\dfrac{grams\: of\: substance}{moles\: of\: substance}}=\dfrac{m}{n} \nonumber \]
Ідеальне рівняння газу можна переставити, щоб виділити n:
\[n=\dfrac{PV}{RT} \nonumber \]
а потім поєднується з рівнянням молярної маси для отримання:
\[ℳ=\dfrac{mRT}{PV} \nonumber \]
Це рівняння може бути використано для отримання молярної маси газу з вимірювань його тиску, об'єму, температури та маси.
Приблизну молярну масу летючої рідини можна визначити за допомогою:
- Нагрівання зразка рідини в колбі з крихітним отвором у верхній частині, яке перетворює рідину в газ, який може вийти через отвір
- Зняття колби з тепла в той момент, коли останній біт рідини стане газом, в цей час колба буде заповнена тільки газоподібним зразком під тиском навколишнього середовища
- Герметизація колби і дозвіл газоподібного зразка конденсуватися в рідину, а потім зважування колби для визначення маси зразка (рис.\(\PageIndex{1}\))

За допомогою цієї процедури зразок хлороформного газу масою 0,494 г збирають у колбу об'ємом 129 см 3 при 99,6 °С при атмосферному тиску 742,1 мм рт.ст. Яка приблизна молярна маса хлороформу?
Рішення
Так як
\[ℳ=\dfrac{m}{n} \nonumber \]
і
\[n=\dfrac{PV}{RT} \nonumber \]
підставляючи і переставляючи дає
\[ℳ=\dfrac{mRT }{PV} \nonumber \]
потім
\[ℳ=\dfrac{mRT}{PV}=\mathrm{\dfrac{(0.494\: g)×0.08206\: L⋅atm/mol\: K×372.8\: K}{0.976\: atm×0.129\: L}=120\:g/mol} \nonumber \]
Зразок фосфору, який важить 3,243 × 10 −2 г, надає тиск 31,89 кПа в колбі 56,0 мл при 550° С Які молярна маса і молекулярна формула пари фосфору?
- Відповідь
-
124 г/моль Р 4
Тиск суміші газів: закон Дальтона
Якщо вони хімічно не вступають в реакцію один з одним, окремі гази в суміші газів не впливають на тиск один одного. Кожен окремий газ в суміші чинить той самий тиск, який він чинив би, якби він був присутній один в ємності (рис.\(\PageIndex{2}\)). Тиск, який чинить кожен окремий газ в суміші, називається її парціальним тиском. Це спостереження узагальнено законом Дальтона парціальних тисків: Загальний тиск суміші ідеальних газів дорівнює сумі парціальних тисків складових газів:
\[P_{Total}=P_A+P_B+P_C+...=\sum_iP_i \nonumber \]
У рівнянні Р Загальний - сумарний тиск суміші газів, Р А - парціальний тиск газу А; P B - парціальний тиск газу B; P C - парціальний тиск газу С; і так далі.

Парціальний тиск газу А пов'язаний із загальним тиском газової суміші через її мольну фракцію (X), одиницю концентрації, визначену як кількість молів компонента розчину, поділеного на загальну кількість молів всіх компонентів:
\[P_A=X_A×P_{Total}\hspace{20px}\ce{where}\hspace{20px}X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
де P A, X A, і n A - парціальний тиск, моль фракція, і число молів газу A відповідно, а n Всього - число молів всіх компонентів в суміші.
Судина об'ємом 10,0 л містить 2,50 × 10 −3 моль H 2, 1,00 × 10 −3 моль He та 3,00 × 10 −4 моль Ne при 35° C.
- Які парціальні тиски кожного з газів?
- Що таке сумарний тиск в атмосферах?
Рішення
Гази поводяться самостійно, тому парціальний тиск кожного газу можна визначити за ідеальним рівнянням газу, використовуючи\(P=\dfrac{nRT}{V}\):
\[P_\mathrm{H_2}=\mathrm{\dfrac{(2.50×10^{−3}\:mol)(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=6.32×10^{−3}\:atm} \nonumber \]
\[P_\ce{He}=\mathrm{\dfrac{(1.00×10^{−3}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=2.53×10^{−3}\:atm} \nonumber \]
\[P_\ce{Ne}=\mathrm{\dfrac{(3.00×10^{−4}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=7.58×10^{−4}\:atm} \nonumber \]
Загальний тиск задається сумою парціальних тисків:
\[P_\ce{T}=P_\mathrm{H_2}+P_\ce{He}+P_\ce{Ne}=\mathrm{(0.00632+0.00253+0.00076)\:atm=9.61×10^{−3}\:atm} \nonumber \]
Колба 5,73 л при 25 °С містить 0,0388 моль N 2, 0,147 моль СО та 0,0803 моль H 2. Яке загальний тиск в колбі в атмосферах?
- Відповідь
-
1,137 атм
Ось ще один приклад цього поняття, але має справу з розрахунками моль фракції.
Газова суміш, яка використовується для анестезії, містить 2,83 моль кисню, О 2 і 8,41 моль закису азоту, N 2 O. Загальний тиск суміші становить 192 кПа.
- Які мольні фракції O 2 і N 2 O?
- Які парціальні тиски O 2 і N 2 O?
Рішення
Мольова фракція задається
\[X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
і парціальний тиск
\[P_A = X_A \times P_{Total} \nonumber \]
Для O 2,
\[X_{O_2}=\dfrac{n_{O_2}}{n_{Total}}=\mathrm{\dfrac{2.83 mol}{(2.83+8.41)\:mol}=0.252} \nonumber \]
і
\[P_{O_2}=X_{O_2}×P_{Total}=\mathrm{0.252×192\: kPa=48.4\: kPa} \nonumber \]
Для N 2 О,
\[X_{N_2O}=\dfrac{n_{N_2O}}{n_{Total}}=\mathrm{\dfrac{8.41\: mol}{(2.83+8.41)\:mol}=0.748} \nonumber \]
і
\[P_{N_2O}=X_{N_2O}×P_{Total}=\mathrm{(0.748)×192\: kPa = 143.6 \: kPa} \nonumber \]
Який тиск суміші 0,200 г Н 2, 1,00 г N 2 і 0,820 г Ar в ємності об'ємом 2,00 л при 20 °C?
- Відповідь
-
1,87 атм
Збір газів над водою
Простий спосіб збору газів, які не вступають в реакцію з водою, - це захоплення їх у пляшку, наповнену водою і перевернуту в посуд, наповнену водою. Тиск газу всередині пляшки можна зробити рівним тиску повітря зовні шляхом підняття або опускання пляшки. Коли рівень води однаковий як всередині, так і зовні пляшки (рис.\(\PageIndex{3}\)), тиск газу дорівнює атмосферному тиску, яке можна виміряти за допомогою барометра.
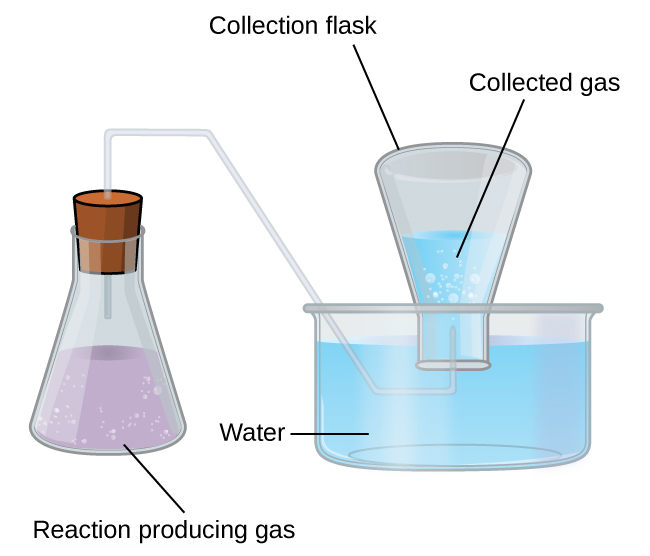
Однак є ще один фактор, який ми повинні враховувати, коли вимірюємо тиск газу цим методом. Вода випаровується і завжди є газоподібна вода (водяна пара) над зразком рідкої води. У міру збору газу над водою він насичується водяною парою і загальний тиск суміші дорівнює парціальному тиску газу плюс парціальний тиск водяної пари. Таким чином, тиск чистого газу дорівнює загальному тиску мінус тиск водяної пари - це називається «сухим» тиском газу, тобто тиском лише газу, без водяної пари.
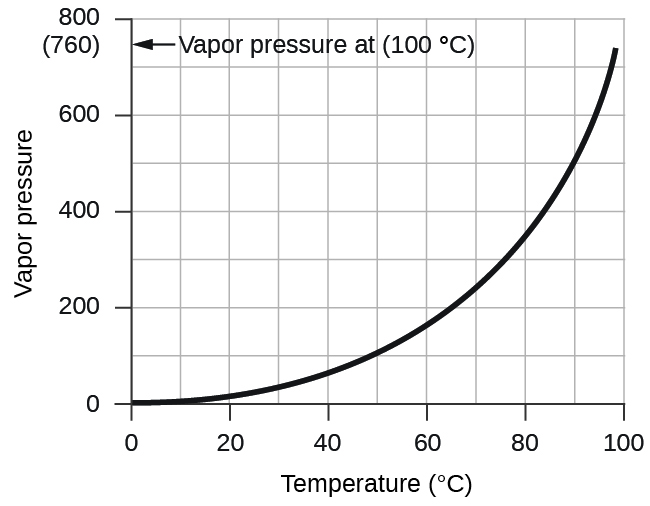
Тиск пари води, що представляє собою тиск, що чиниться водяною парою в рівновазі з рідкою водою в закритій ємності, залежить від температури (рис.\(\PageIndex{4}\)); більш детальну інформацію про температурну залежність водяної пари можна знайти в табл.\(\PageIndex{1}\), а пари про тиск буде розглянуто більш докладно в наступному розділі про рідини.
| Температура (°C) | Тиск (торр) | Температура (°C) | Тиск (торр) | Температура (°C) | Тиск (торр) | ||
|---|---|---|---|---|---|---|---|
| —10 | 1,95 | 18 | 15.5 | 30 | 31.8 | ||
| -5 | 3.0 | 19 | 16.5 | 35 | 42.2 | ||
| —2 | 3.9 | 20 | 17.5 | 40 | 55.3 | ||
| 0 | 4.6 | 21 | 18.7 | 50 | 92.5 | ||
| 2 | 5.3 | 22 | 19.8 | 60 | 149.4 | ||
| 4 | 6.1 | 23 | 21.1 | 70 | 233.7 | ||
| 6 | 7.0 | 24 | 22.4 | 80 | 355.1 | ||
| 8 | 8.0 | 25 | 23.8 | 90 | 525.8 | ||
| 10 | 9.2 | 26 | 25.2 | 95 | 633.9 | ||
| 12 | 10.5 | 27 | 26.7 | 99 | 733.2 | ||
| 14 | 12.0 | 28 | 28.3 | 100.0 | 760.0 | ||
| 16 | 13,6 | 29 | 30.0 | 101.0 | 787.6 |
Якщо 0,200 л аргону збирається над водою при температурі 26° C і тиску 750 торр в системі, подібній до наведеної на малюнку\(\PageIndex{3}\), що таке парціальний тиск аргону?
Рішення
Згідно із законом Дальтона, загальний тиск в пляшці (750 торр) - це сума парціального тиску аргону і парціального тиску газоподібної води:
\[P_\ce{T}=P_\ce{Ar}+P_\mathrm{H_2O} \nonumber \]
Перестановка цього рівняння для розв'язання для тиску аргону дає:
\[P_\ce{Ar}=P_\ce{T}−P_\mathrm{H_2O} \nonumber \]
Тиск водяної пари над зразком рідкої води при 26° С становить 25,2 торр (Додаток Е), так:
\[P_\ce{Ar}=\mathrm{750\:torr−25.2\:torr=725\:torr} \nonumber \]
Зразок кисню, зібраний над водою при температурі 29,0 °С і тиску 764 торр, має об'єм 0,560 л. Який обсяг мав би сухий кисень за тих же умов температури і тиску?
- Відповідь
-
0.583 Л
Хімічна стехіометрія і гази
Хімічна стехіометрія описує кількісні співвідношення між реагентами і продуктами в хімічних реакціях. Раніше ми вимірювали кількості реагентів та продуктів, використовуючи маси для твердих тіл та об'ємів у поєднанні з молярністю для розчинів; тепер ми також можемо використовувати обсяги газу для позначення кількостей. Якщо ми знаємо об'єм, тиск і температуру газу, ми можемо використовувати ідеальне рівняння газу, щоб обчислити, скільки молів газу присутній. Якщо ми знаємо, скільки молів газу задіяно, ми можемо обчислити обсяг газу при будь-якій температурі і тиску.
Закон Авогадро переглянуто
Іноді ми можемо скористатися спрощеною особливістю стехіометрії газів, яку тверді речовини та розчини не виявляють: всі гази, які демонструють ідеальну поведінку, містять однакову кількість молекул в однаковому обсязі (при однаковій температурі та тиску). Таким чином, співвідношення обсягів газів, що беруть участь в хімічній реакції, задаються коефіцієнтами в рівнянні для реакції за умови, що обсяги газу вимірюються при однаковій температурі і тиску.
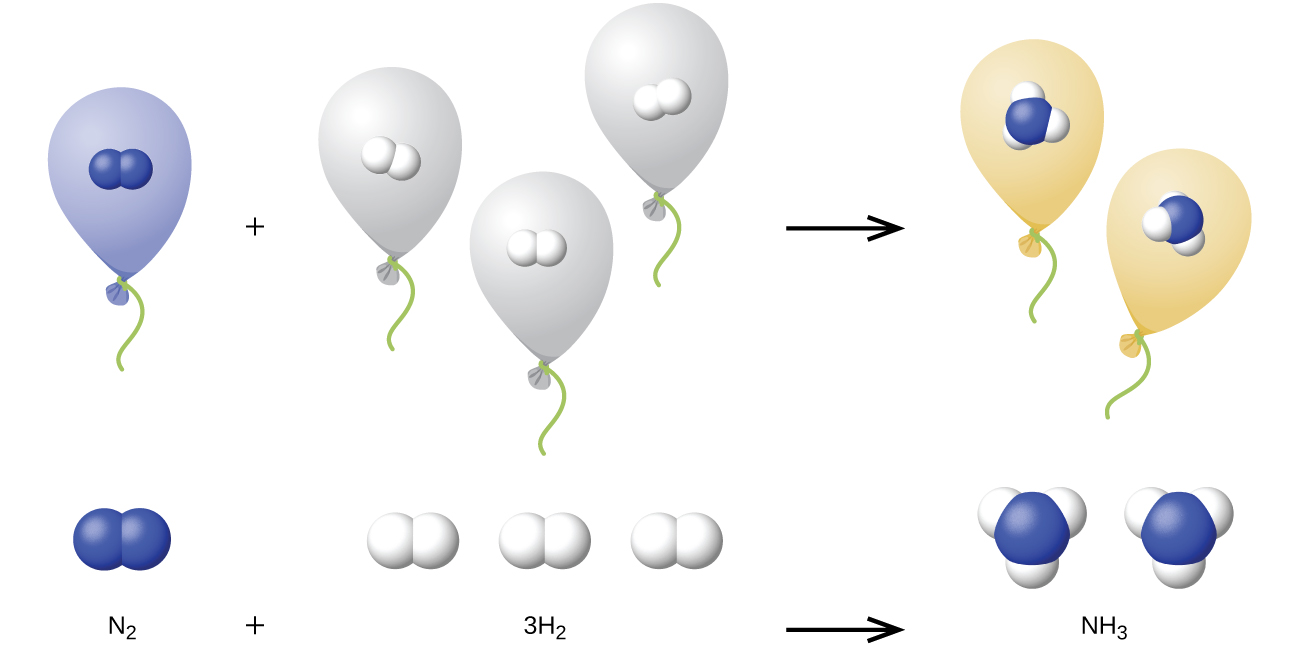
Ми можемо поширити закон Авогадро (що обсяг газу прямо пропорційний кількості молів газу) на хімічні реакції з газами: Гази об'єднуються або реагують у певних і простих пропорціях за обсягом, за умови, що всі обсяги газу вимірюються при однаковій температурі і тиску. Наприклад, оскільки азотні та водневі гази реагують на отримання газу аміаку відповідно до
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
заданий обсяг газу азоту реагує з триразовим об'ємом водню газу, щоб виробляти в два рази більше обсягу аміачного газу, якщо тиск і температура залишаються постійними.
Пояснення цьому проілюстровано на рис\(\PageIndex{4}\). Згідно із законом Авогадро, рівні обсяги газоподібних N 2, H 2 і NH 3 при однаковій температурі і тиску містять однакову кількість молекул. Оскільки одна молекула N 2 реагує з трьома молекулами H 2 для отримання двох молекул NH 3, необхідний об'єм H 2 втричі перевищує об'єм N 2, а обсяг виробленого NH 3 в два рази перевищує об'єм N 2.
Пропан, С 3 Н 8 (г), використовується в газових грилі для забезпечення тепла для приготування їжі. Який об'єм O 2 (g), виміряний при 25° C і 760 torr, необхідний для реагування з 2,7 л пропану, виміряного в тих же умовах температури і тиску? Припустимо, що пропан піддається повному згорянню.
Рішення
Співвідношення обсягів С 3 Н 8 і О 2 буде дорівнює відношенню їх коефіцієнтів в збалансованому рівнянні для реакції:
\ [\ почати {вирівняти}
&\ ce {C3H8} (г) +\ ce {5O2} (г) ⟶ &&\ ce {3CO2} (г) +\ ce {4H2O} (л)\
\ ce {&1\: обсяг + 5\: томи &3\: томи + 4\: томи}
\ кінець {вирівнювання}\ номер\]
З рівняння бачимо, що один обсяг С 3 Н 8 буде реагувати з п'ятьма обсягами О 2:
\[\mathrm{2.7\cancel{L\:C_3H_8}×\dfrac{5\: L\:\ce{O2}}{1\cancel{L\:C_3H_8}}=13.5\: L\:\ce{O2}} \nonumber \]
Обсяг 13,5 л О 2 буде потрібно для реакції з 2,7 л С 3 Н 8.
Ацетиленовий бак для оксиацетиленового зварювального пальника забезпечує 9340 л ацетиленового газу, C 2 H 2, при 0° C і 1 атм. Скільки резервуарів кисню, кожен з яких забезпечує 7,00 × 10 3 л O 2 при 0° C і 1 атм, буде потрібно для спалювання ацетилену?
\[\ce{2C2H2 + 5O2⟶4CO2 + 2H2O} \nonumber \]
- Відповідь
-
3.34 резервуари (2,34 × 10 4 л)
Аміак є важливим добривом і промисловим хімічним речовиною. Припустимо, що було виготовлено обсяг 683 мільярдів кубічних футів газоподібного аміаку, виміряний при 25° C і 1 атм. Який обсяг Н 2 (г), виміряний при тих же умовах, знадобився для приготування цієї кількості аміаку реакцією з N 2?
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
Рішення
Оскільки рівні обсяги H 2 і NH 3 містять однакові числа молекул і кожні три молекули Н 2, які реагують, виробляють дві молекули NH 3, співвідношення об'ємів H 2 і NH 3 буде дорівнює 3:2. Два томи NH 3, в даному випадку в одиницях мільярда футів 3, будуть сформовані з трьох томів H 2:
\[\mathrm{683\cancel{billion\:ft^3\:NH_3}×\dfrac{3\: billion\:ft^3\:H_2}{2\cancel{billion\:ft^3\:NH_3}}=1.02×10^3\:billion\:ft^3\:H_2} \nonumber \]
Виробництво 683 мільярдів футів 3 з NH 3 вимагало 1020 мільярдів футів 3 H 2. (При 25° C і 1 атм це обсяг куба з довжиною краю приблизно 1,9 милі.)
Який об'єм O 2 (g), виміряний при 25° C і 760 торр, необхідний для реагування з 17,0 л етилену, C 2 H 4 (g), виміряного в тих же умовах температури і тиску? Продукція - СО 2 і водяна пара.
- Відповідь
-
51.0 Л
Який об'єм водню при 27 °С і 723 торр можна отримати при реакції 8,88 г галію з надлишком соляної кислоти?
\[\ce{2Ga}(s)+\ce{6HCl}(aq)⟶\ce{2GaCl3}(aq)+\ce{3H2}(g) \nonumber \]
Уціон грунту
Щоб перевести з маси галію в обсяг Н 2 (г), нам потрібно зробити приблизно так:

Перші дві конверсії:
\[\mathrm{8.88\cancel{g\: Ga}×\dfrac{1\cancel{mol\: Ga}}{69.723\cancel{g\: Ga}}×\dfrac{3\: mol\:H_2}{2\cancel{mol\: Ga}}=0.191\:mol\: H_2} \nonumber \]
Нарешті, ми можемо скористатися ідеальним газовим законом:
\[V_\mathrm{H_2}=\left(\dfrac{nRT}{P}\right)_\mathrm{H_2}=\mathrm{\dfrac{0.191\cancel{mol}×0.08206\: L\cancel{atm\:mol^{−1}\:K^{−1}}×300\: K}{0.951\:atm}=4.94\: L} \nonumber \]
Діоксид сірки є проміжним продуктом при отриманні сірчаної кислоти. Який обсяг SO 2 при 343° C і 1,21 атм утворюється при спалюванні l.00 кг сірки в кисні?
- Відповідь
-
1,30 × 10 3 Л
Тонка шкіра нашої атмосфери утримує землю від крижаної планети і робить її придатною для життя. Насправді це пов'язано з менш ніж 0,5% молекул повітря. З енергії сонця, яка досягає землі, майже\(\dfrac{1}{3}\) відбивається назад у космос, а решта поглинається атмосферою та поверхнею землі. Частина енергії, яку поглинає земля, повторно випромінюється у вигляді інфрачервоного (ІЧ) випромінювання, частина якого проходить назад через атмосферу в космос. Однак більша частина цього ІЧ-випромінювання поглинається певними речовинами в атмосфері, відомими як парникові гази, які повторно випромінюють цю енергію у всіх напрямках, затримуючи частину тепла. Це підтримує сприятливі умови життя - без атмосфери середня глобальна температура 14° C (57° F) становила б близько -19° C (-2° F). Основними парниковими газами (ПГ) є водяна пара, вуглекислий газ, метан та озон. З часів промислової революції людська діяльність збільшувала концентрації парникових газів, які змінили енергетичний баланс і значно змінюють клімат землі (рис.\(\PageIndex{6}\)).
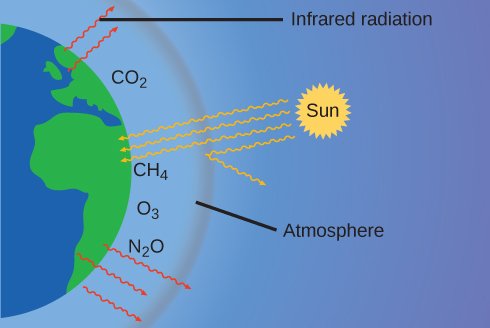
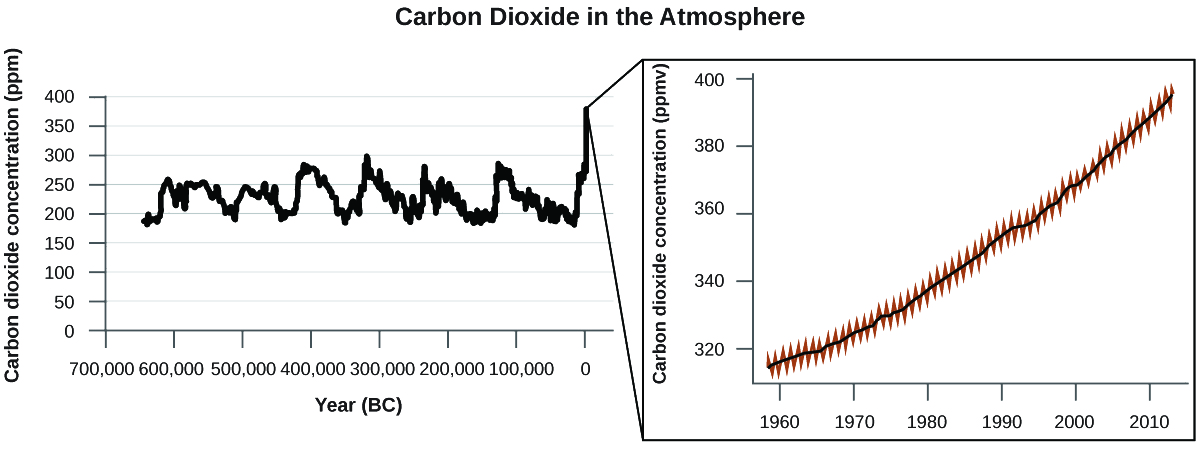
З багатьох джерел є вагомі докази того, що більш високі атмосферні рівні CO 2 викликані людською діяльністю, при цьому спалювання\(\dfrac{3}{4}\) викопного палива становить приблизно недавнє збільшення CO 2. Достовірні дані крижаних сердечників показують, що концентрація CO 2 в атмосфері знаходиться на найвищому рівні за останні 800 000 років; інші дані свідчать про те, що вона може бути на найвищому рівні за 20 мільйонів років. В останні роки концентрація CO 2 зросла з історичних рівнів нижче 300 ppm до майже 400 ppm сьогодні (рис.\(\PageIndex{7}\)).
Резюме
Закон ідеального газу може бути використаний для отримання ряду зручних рівнянь, що стосуються безпосередньо виміряних величин до властивостей, що представляють інтерес для газоподібних речовин і сумішей. Відповідна перестановка рівняння ідеального газу може бути здійснена, щоб дозволити розрахунок щільності газу та молярних мас. Закон Дальтона парціальних тисків може бути використаний для зв'язку виміряних тисків газу для газових сумішей з їх складами. Закон Авогадро може бути використаний в стехіометричних розрахунках для хімічних реакцій за участю газоподібних реагентів або продуктів.
Ключові рівняння
- P Всього = П А+П Б + П С +... = i П i
- Р А = Х А П Всього
- \(X_A=\dfrac{n_A}{n_{Total}}\)
Виноски
- «Цитати Джозеф-Луї Лагранжа», останній модифікований лютий 2006 року, доступ до лютого 10, 2015, www-history.mcs.st-andrews.ac... /Lagrange.html
Резюме
- Закон Дальтона парціальних тисків
- загальний тиск суміші ідеальних газів дорівнює сумі парціальних тисків складових газів.
- моль фракція (X)
- одиниця концентрації визначається як відношення молярної кількості компонента суміші до загальної кількості молів всіх компонентів суміші
- парціальний тиск
- тиск, що чиниться окремим газом в суміші
- тиск пари води
- тиск, що чиниться водяною парою в рівновазі з рідкою водою в закритій ємності при певній температурі
