9.4: Випіт і дифузія газів

Last updated
Save as PDF

Page ID: 22738

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

↑

Цілі навчання

Визначте та поясніть випіт та дифузію
Державний закон Грема і використовувати його для обчислення відповідних властивостей газу

Якщо ви коли-небудь були в кімнаті, коли була доставлена гаряча піца, ви були обізнані про те, що газоподібні молекули можуть швидко поширюватися по всій кімнаті, про що свідчить приємний аромат, який незабаром досягає вашого носа. Хоча газоподібні молекули рухаються з величезною швидкістю (сотні метрів в секунду), вони стикаються з іншими газоподібними молекулами і рухаються в самих різних напрямках, перш ніж досягти бажаної мети. При кімнатній температурі газоподібна молекула буде відчувати мільярди зіткнень в секунду. Середній вільний шлях - це середня відстань, яку молекула проходить між зіткненнями. Середній вільний шлях збільшується зі зменшенням тиску; загалом середній вільний шлях для газоподібної молекули буде в сотні разів більше діаметра молекули

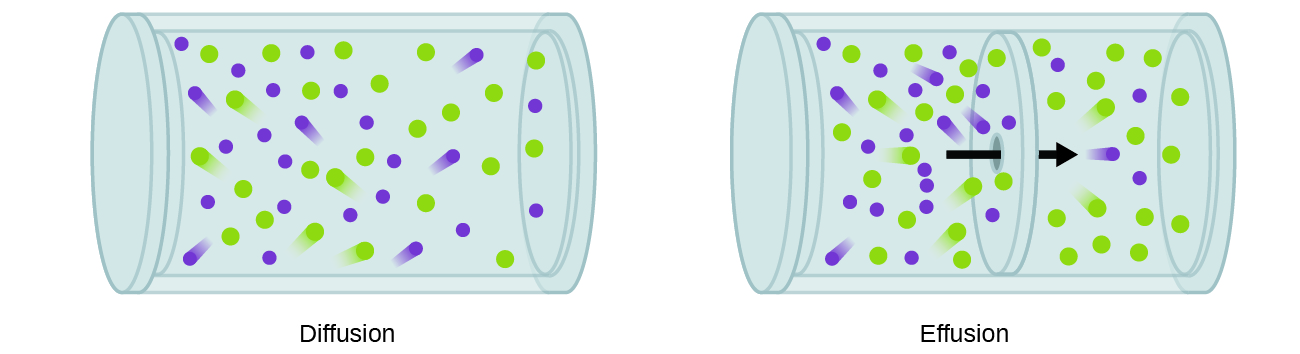
Взагалі ми знаємо, що при введенні зразка газу в одну частину закритого контейнера його молекули дуже швидко розходяться по всій ємності; цей процес, за допомогою якого молекули розсіюються в просторі у відповідь на відмінності в концентрації, називається дифузією (показаний на рис.\(\PageIndex{1}\)) . Газоподібні атоми або молекули, звичайно, не знають жодного градієнта концентрації, вони просто рухаються випадковим чином - області з вищою концентрацією мають більше частинок, ніж регіони менших концентрацій, і тому відбувається чистий рух видів від областей високої до низької концентрації. У закритому середовищі дифузія в кінцевому підсумку призведе до однакових концентрацій газу по всьому, як показано на малюнку\(\PageIndex{1}\). Газоподібні атоми і молекули продовжують рухатися, але оскільки їх концентрації однакові в обох лампочках, швидкості передачі між цибулинами рівні (чистий перенос молекул не відбувається).

Малюнок\(\PageIndex{1}\): (а) Спочатку розділені два гази, H ₂ _{і O 2}. (б) Коли запірний кран відкритий, вони змішуються між собою. Легший газ, Н ₂, проходить через отвір швидше, ніж О ₂, тому відразу після відкриття запірного крана більше молекул Н ₂ переміщається в сторону O ₂, ніж молекули O ₂ переміщаються в сторону Н ₂. (c) Через короткий час як повільніше рухаються молекули O ₂, так і більш швидкі молекули H ₂ розподілилися рівномірно по обидва боки судини.

Нас часто цікавить швидкість дифузії, кількість газу, що проходить через якусь площу в одиницю часу:

\[\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}} \nonumber \]

Швидкість дифузії залежить від декількох факторів: градієнта концентрації (збільшення або зменшення концентрації від однієї точки до іншої); кількості площі поверхні, доступної для дифузії; і відстані, яку повинні пройти частинки газу. Зверніть увагу також, що час, необхідний для дифузії, обернено пропорційний швидкості дифузії, як показано в рівнянні швидкості дифузії.

Процес, що включає рух газоподібних видів, схожих на дифузію, - це випіт, вихід молекул газу через крихітний отвір, такий як точкове отвір у повітряній кулі, у вакуум (рис.\(\PageIndex{1}\)). Хоча швидкість дифузії та випоту залежать від молярної маси задіяного газу, їх швидкості не рівні; однак співвідношення їх швидкостей однакові.

Малюнок\(\PageIndex{2}\): Дифузія відбувається, коли молекули газу розсіюються по всій ємності. Випіт виникає, коли газ проходить через отвір, менший за середній вільний шлях частинок, тобто середня відстань, пройдена між зіткненнями. Ефективно це означає, що за раз проходить тільки одна частинка.

Якщо суміш газів помістити в ємність з пористими стінками, гази стікають через невеликі отвори в стінках. Більш легкі гази проходять через невеликі отвори швидше (з більшою швидкістю), ніж важчі (рис.\(\PageIndex{2}\)). У 1832 році Томас Грем вивчив швидкості випоту різних газів і сформулював закон Грема випоту: Швидкість випоту газу обернено пропорційна квадратному кореню маси його частинок:

\[\textrm{rate of effusion}∝\dfrac{1}{\sqrt{ℳ}} \nonumber \]

Це означає, що якщо два гази А і В знаходяться при однаковій температурі і тиску, то співвідношення швидкостей їх випоту обернено пропорційно відношенню квадратних коренів мас їх частинок:

\[\dfrac{\textrm{rate of effusion of B}}{\textrm{rate of effusion of A}}=\dfrac{\sqrt{ℳ_\ce{A}}}{\sqrt{ℳ_\ce{B}}} \nonumber \]

Малюнок\(\PageIndex{3}\): Повітряна куля, наповнена повітрям (синій), залишається повноцінним протягом ночі. Повітряна куля, наповнена гелієм (зеленим), частково здувається, оскільки менші, легкі атоми гелію стікають через невеликі отвори в гумі набагато легше, ніж важчі молекули азоту та кисню, що знаходяться в повітрі. (кредит: модифікація роботи Марка Отта)

Приклад\(\PageIndex{1}\): Applying Graham’s Law to Rates of Effusion

Обчисліть відношення швидкості випоту водню до швидкості випоту кисню.

Рішення

З закону Грема, ми маємо:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{\sqrt{1.43\cancel{g\: L^{−1}}}}{\sqrt{0.0899\cancel{g\: L^{−1}}}}=\dfrac{1.20}{0.300}=\dfrac{4}{1}} \nonumber \]

Використання молярних мас:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{32\cancel{g\: mol^{−1}}}{2\cancel{g\: mol^{−1}}}=\dfrac{\sqrt{16}}{\sqrt{1}}=\dfrac{4}{1}} \nonumber \]

Водень витікає в чотири рази швидше, ніж кисень.

Вправа\(\PageIndex{1}\)

При певному тиску і температурі газ азот витікає зі швидкістю 79 мл/с.Використовуючи той же апарат при однаковій температурі і тиску, з якою швидкістю буде стікати діоксид сірки?

Відповідь: 52 мл/с

Ось ще один приклад, роблячи точку про те, як визначення часу відрізняється від визначення ставок.

Приклад\(\PageIndex{2}\): Effusion Time Calculations

Це займає 243 с для 4,46 × 10 ⁻⁵ моль Xe, щоб стікати через крихітний отвір. За тих же умов, скільки часу знадобиться 4,46 × 10 ⁻⁵ моль Ne для стікання?

Рішення

Важливо протистояти спокусі використовувати час безпосередньо, і пам'ятати, як ставка відноситься до часу, а також як вона відноситься до маси. Нагадаємо визначення швидкості випоту:

\[\textrm{rate of effusion}=\dfrac{\textrm{amount of gas transferred}}{\textrm{time}}\nonumber \]

і поєднайте його із законом Грема:

\[\dfrac{\textrm{rate of effusion of gas Xe}}{\textrm{rate of effusion of gas Ne}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Щоб отримати:

\[\dfrac{\dfrac{\textrm{amount of Xe transferred}}{\textrm{time for Xe}}}{\dfrac{\textrm{amount of Ne transferred}}{\textrm{time for Ne}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Відзначивши, що сума A = кількість B, і рішення для часу для Ne:

\[\dfrac{\dfrac{\cancel{\textrm{amount of Xe}}}{\textrm{time for Xe}}}{\dfrac{\cancel{\textrm{amount of Ne}}}{\textrm{time for Ne}}}=\dfrac{\textrm{time for Ne}}{\textrm{time for Xe}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}} \nonumber \]

і підставляють значення:

\[\mathrm{\dfrac{time\: for\: Ne}{243\:s}=\sqrt{\dfrac{20.2\cancel{g\: mol}}{131.3\cancel{g\: mol}}}=0.392}\nonumber \]

Нарешті, вирішіть бажану кількість:

\[\mathrm{time\: for\: Ne=0.392×243\:s=95.3\:s}\nonumber \]

Зверніть увагу, що ця відповідь є розумною: оскільки Ne легше, ніж Xe, швидкість випоту для Ne буде більшою, ніж для\(\ce{Xe}\), а це означає, що час випоту для Ne буде меншим, ніж для Xe.

Вправа\(\PageIndex{2}\)

Повітряна куля, наповнена гелієм, здувається до\(\dfrac{2}{3}\) початкового об'єму за 8.0 годин. Скільки часу знадобиться ідентична повітряна куля, наповнена такою ж кількістю молів повітря (= 28,2 г/моль), щоб здути до\(\dfrac{1}{2}\) початкового об'єму?

Відповідь: 32 год

Нарешті, ось ще один приклад, який показує, як розрахувати молярну масу за даними швидкості випоту.

Приклад\(\PageIndex{3}\): Determining Molar Mass Using Graham’s Law

Невідомий газ випливає в 1,66 рази швидше, ніж СО ₂. Яка молярна маса невідомого газу? Чи можете ви зробити розумне припущення щодо його ідентичності?

Рішення

З закону Грема, ми маємо:

\[\mathrm{\dfrac{rate\: of\: effusion\: of\: Unknown}{rate\: of\: effusion\: of\: CO_2}}={\sqrt{ℳ_\mathrm{CO_2}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Підключіть відомі дані:

\[\dfrac{1.66}{1}=\dfrac{\sqrt{44.0\:\ce{g/mol}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Вирішити:

\[ℳ_{Unknown}=\mathrm{\dfrac{44.0\:g/mol}{(1.66)^2}=16.0\:g/mol} \nonumber \]

Газом цілком міг бути СН ₄, єдиний газ з цією молярною масою.

Вправа

Газ водень стікає через пористу ємність в 8,97 разів швидше, ніж невідомий газ. Оцініть молярну масу невідомого газу.

Відповідь: 163 г/моль

Застосування: Використання дифузії для збагачення урану

Газоподібна дифузія була використана для отримання збагаченого урану для використання на атомних електростанціях та озброєнні. Природний уран містить лише 0,72% ²³⁵ U, виду урану, який є «ділиться», тобто здатним підтримувати ланцюгову реакцію ядерного поділу. Ядерні реактори вимагають палива, яке становить 2— 5% ²³⁵ U, а ядерні бомби потребують ще більших концентрацій. Один із способів збагачення урану до бажаних рівнів - скористатися законом Грема. У газоподібному дифузійному збагачувальному заводі гексафторид урану (UF ₆, єдине з'єднання урану, яке досить летюче для роботи) повільно перекачується через великі циліндричні судини, звані дифузорами, які містять пористі бар'єри з мікроскопічними отворами. Процес є одним з дифузій, оскільки інша сторона бар'єру не евакуйована. Молекули ²³⁵ UF ₆ мають вищу середню швидкість і розсіюють через бар'єр трохи швидше, ніж важчі молекули ²³⁸ UF ₆. Газ, який пройшов через бар'єр, трохи збагачений в ²³⁵ UF ₆ і залишковий газ трохи виснажується. Невелика різниця в молекулярних масах між ²³⁵ UF ₆ і ²³⁸ UF ₆ лише близько 0,4% збагачення, досягається в одному дифузорі (рис.\(\PageIndex{4}\)). Але шляхом підключення багатьох дифузорів в послідовності ступенів (званих каскадом), можна досягти бажаного рівня збагачення.

Малюнок\(\PageIndex{4}\): У дифузорі газоподібний UF ₆ перекачується через пористий бар'єр, який частково відокремлює ²³⁵ UF ₆ від ²³⁸ UF ₆ UF ₆ повинен пройти через багато великих дифузорних установок для досягнення достатнього збагачення в ²³⁵У.

Широкомасштабне відділення газоподібного ²³⁵ UF ₆ від ²³⁸ UF ₆ було вперше зроблено під час Другої світової війни, на установці атомної енергії в Оук-Рідж, штат Теннессі, в рамках Манхеттенського проекту (розробка першої атомної бомби). Хоча теорія проста, це вимагало подолання багатьох складних технічних проблем, щоб змусити її працювати на практиці. Бар'єр повинен мати крихітні, рівномірні отвори (близько ^10-6 см в діаметрі) і бути досить пористим для отримання високих витрат. Всі матеріали (бар'єр, трубки, поверхневі покриття, мастильні матеріали та прокладки) повинні бути в змозі містити, але не реагувати з, високореактивний і корозійний UF ₆.

Оскільки газоподібні дифузійні установки вимагають дуже великої кількості енергії (для стиснення газу до необхідних високих тисків і проганяти його через каскад дифузора, для видалення тепла, що утворюється під час стиснення тощо), зараз він замінюється технологією газової центрифуги, яка вимагає набагато менше енергії. Нинішня гаряча політична проблема полягає в тому, як заперечити цю технологію Ірану, щоб запобігти виробництву достатньої кількості збагаченого урану, щоб вони могли використовувати для виготовлення ядерної зброї.

Резюме

Газоподібні атоми і молекули вільно і безладно рухаються через простір. Дифузія - це процес, за допомогою якого газоподібні атоми і молекули переносяться з областей відносно високої концентрації в області відносно низької концентрації. Випіт - це подібний процес, при якому газоподібні види переходять з контейнера у вакуум через дуже маленькі отвори. Швидкості випоту газів обернено пропорційні квадратним кореням їх щільності або квадратним кореням мас їх атомів/молекул (закон Грема).

Ключові рівняння

\(\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}}\)
\(\dfrac{\textrm{rate of effusion of gas B}}{\textrm{rate of effusion of gas A}}=\dfrac{\sqrt{m_B}}{\sqrt{m_A}}=\dfrac{\sqrt{ℳ_B}}{\sqrt{ℳ_A}}\)

Резюме

дифузії: рух атома або молекули з області відносно високої концентрації до відносно низької концентрації (розглядається в цьому розділі стосовно газоподібних видів, але застосовується до видів у будь-якій фазі)

виділення: перенесення газоподібних атомів або молекул з контейнера у вакуум через дуже маленькі отвори

Закон Грема випоту: швидкості дифузії і випоту газів обернено пропорційні квадратним кореням їх молекулярних мас

означає вільний шлях: середня відстань, яку молекула рухається між зіткненнями

швидкість дифузії: кількість газу, що дифундує через задану площу протягом заданого часу