6.3: Закон Далтона
- Page ID
- 19139
Переконайтеся, що ви добре розумієте наступні основні ідеї, які були представлені нижче.
- Один моль газу займає обсяг 22,4 л при СТП (стандартна температура і тиск, 273К, 1 атм = 103 кПа.)
- Вищевказаний факт дозволяє співвіднести вимірювану властивість щільності газу з його молярною масою.
- Склад суміші газів зазвичай виражається термінами мольних фракцій; будьте впевнені, що знаєте, як їх розрахувати.
- Закон Дальтона про парціальний тиск говорить, що кожен газ у суміші діє незалежно, тому загальний тиск газу, який чинить на стінки контейнера, є лише сумою парціальних тисків окремих компонентів.
Хоча всі гази уважно дотримуються ідеального закону газу PV = nRT при відповідних умовах, кожен газ також є унікальною хімічною речовиною, що складається з молекулярних одиниць, які мають певні маси. У цьому уроці ми побачимо, як ці молекулярні маси впливають на властивості газів, які відповідають закону ідеального газу. Після цього ми розглянемо гази, які містять більше одного виду molecula— іншими словами, суміші газів. Почнемо з огляду молярного об'єму та принципу E.V.E.N., який є центральним у нашому розумінні газових сумішей.
Молярний об'єм газу
Ви нагадаєте, що молярна маса чистої речовини - це маса 6,02 х 10 23 (число Авогадро) частинок або молекулярних одиниць цієї речовини. Молярні маси зазвичай виражаються в одиницях грамів на моль (g моль —1) і часто називаються молекулярною масою s. як було пояснено в попередньому уроці, рівні обсяги газів, виміряні при однаковій температурі і тиску, містять рівні числа молекул (це Принцип «НАВІТЬ», більш формально відомий як закон Авогадро. ) Стандартна температура і тиск: 273K, 1 атм
Величина цього обсягу, звичайно, буде залежати від температури і тиску, тому в якості засобу зручного порівняння прийнято визначати набір умов Т = 273 К і Р = 1 атм в якості стандартної температури і тиску, зазвичай позначається як STP. Підставляючи ці значення в ідеальне рівняння стану газу і рішення для V виходить обсяг 22,414 л на 1 моль.
Який би об'єм одного моля повітря був при 20° C на вершині Mauna Kea, Hawa'ii (висота 4,2 км), де тиск повітря становить приблизно 60 кПа?

Скорія та шлакові конуси на вершині Мауна-Кеа взимку. (Громадське надбання; USGS)
Рішення
Застосовуйте закони Бойла і Чарльза як послідовні поправочні коефіцієнти до стандартного тиску на рівні моря 101,3 кПа:

Стандартний молярний об'єм 22,4 л моль —1 - це значення, яке варто запам'ятати, але пам'ятайте, що воно дійсне тільки при STP. Молярний об'єм при інших температурах і тисках можна легко знайти за простою пропорцією. Молярний об'єм речовини може сказати нам щось про те, скільки місця займає кожна молекула, як показує наступний приклад.
Оцініть середню відстань між молекулами в газі при тиску 1 атм і 0°С.
Рішення
Враховуйте 1 см 3 обсягу газу, який буде містити
\[\dfrac{6.02 \times 10^{23} \;mol^{–1}}{22,400\; cm^3 \;mol^{–1}} = 2.69 \times 10^{19} cm^{-3} \nonumber\]
Обсяг на молекулу (не такий, як обсяг молекули, який для ідеального газу дорівнює нулю!) це просто взаємне це, або\(3.72 \times 10^{-20}\, cm^3\). Припустимо, що молекули рівномірно розподілені так, що кожна займає уявну коробку, що має цей обсяг. Середня відстань між центрами молекул буде визначатися довжиною цього ящика, який є кубовим коренем обсягу на молекулу:
\[(3.72 \times 10^{–20})^{1/3} = 3.38 \times 10^{–7}\, cm = 3.4\, nm \nonumber\]
В умовах, при яких застосовується ідеальна модель газу (тобто майже завжди, якщо ви не інженер хімік, що займається високими тисками), «молекула - це молекула», тому обсяг кількості молекул Авогадро буде незалежним від складу газу. Причина, звичайно, в тому, що обсяг газу в основному порожній простір; обсяги самих молекул мізерно малі.
Молярна маса і щільність газу
Молекулярна маса (молярна маса) будь-якого газу - це маса, виражена в грамах, кількості його молекул Авогадро. Це вірно незалежно від того, чи складається газ з одного молекулярного виду або являє собою суміш. Для суміші газів молярна маса буде залежати і від молярних мас її компонентів, і від фракційного достатку кожного виду молекули в суміші. Термін «середня молекулярна маса» часто використовується для опису молярної маси газової суміші.
Середня молярна маса (\(\bar{m}\)) суміші газів - це всього лише сума мольних часток кожного газу, помножена на молярну масу цієї речовини:
\[\bar{m}=\sum_i \chi_im_i\]
Знайдіть середню молярну масу сухого повітря, об'єм-склад якого становить O 2 (21%), N 2 (78%) і Ar (1%).
Рішення
Середня молекулярна маса - це моль-фракційна зважена сума молекулярних мас її компонентів. Кротові фракції, звичайно, такі ж, як і об'ємні фракції (принцип E.V.E.N.)
\[m = (0.21 \times 32) + (0.78 \times 28) + (0.01 \times 20) = 28 \nonumber\]
Молярні обсяги всіх газів однакові при вимірюванні при однаковій температурі і тиску. Однак молярні маси різних газів будуть відрізнятися. Це означає, що різні гази матимуть різну щільність (різну масу на одиницю об'єму). Якщо ми знаємо молекулярну масу газу, ми можемо обчислити його щільність.
Газ гексафторид урану UF 6 використовується в ізотопному збагаченні природного урану. Обчисліть його щільність на СТП.
Рішення
Молекулярна маса UF 6 становить 352.
\[\dfrac{352\; g \;mol^{–1}}{22.4\, L\, mol^{–1}} = 15.7\; g\; L^{–1} \nonumber\]
Примітка: немає необхідності шукати «формулу» для цього розрахунку; просто об'єднайте молярну масу і молярний об'єм таким чином, щоб одиниці вийшли правильно.
Що ще важливіше, якщо ми можемо виміряти щільність невідомого газу, ми маємо зручний засіб оцінки його молекулярної маси. Це один з багатьох важливих прикладів того, як макроскопічне вимірювання (зроблене на об'ємній речовині) може дати мікроскопічну інформацію (тобто про об'єкти молекулярного масштабу).
Щільність газу в даний час вимірюється в промисловості за допомогою електромеханічних пристроїв, таких як вібраційний очерет, які можуть забезпечувати безперервні, он-лайн записи в конкретних місцях, як всередині трубопроводів. Визначення молекулярної маси газу за його щільністю відоме як метод Дюма, після того, як його розробив французький хімік Жан Дюма (1800-1840). Один просто вимірює вагу відомого обсягу газу і перетворює цей обсяг в його еквівалент STP, використовуючи закони Бойла і Чарльза. Вага газу, розділений на його обсяг STP, дає щільність газу, а щільність, помножена на 22,4 моль -1, дає молекулярну масу. Зверніть увагу на приклади розрахунків щільності газу, показані тут і в вашому підручнику. Очікується, що ви будете проводити розрахунки такого роду, перетворюючи між молекулярною масою і щільністю газу.
Обчисліть приблизну молярну масу газу, виміряна щільність якого становить 3,33 г/л при 30°C і 780 торр.
Рішення
Знайдіть обсяг, який був би зайнятий 1 л газу на СТП; зверніть увагу, що корекція до 273 К зменшить гучність, а корекція до 1 атм (760 торр) збільшить його:
\[V=(1.00 \mathrm{L})\left(\frac{273}{303}\right)\left(\frac{780}{760}\right)=0.924 \mathrm{L} \nonumber\]
Кількість молів газу становить
\[n = \dfrac{0.924\, L}{22.4\, L\, mol^{–1}}= 0.0412\, mol \nonumber\]
Таким чином, молекулярна маса
\[\dfrac{33\, g\, L^{–1}}{0.0412\, mol\, L^{–1}} = 80.7\, g\, mol^{–1} \nonumber\]
Щільність газової суміші
Вимірювання щільності газу можуть бути корисним засобом оцінки складу суміші двох різних газів; це широко робиться в промислових хімічних операціях, в яких склад газових потоків повинен постійно контролюватися.
Знайдіть склад суміші\(\ce{CO2}\) (44 г/моль) і метану\(\ce{CH4}\) (16 г/моль), яка має щільність STP 1,214 г/л.
Рішення
Щільність суміші цих двох газів буде прямо пропорційна її складу, варіюючись між чистим метаном і чистим СО 2. Почнемо з пошуку цих двох щільностей:
Для СО 2:
(44 г/моль) ÷ (22,4 л/моль) = 1,964 г/л
Для СН 4:
(16 г/моль) ÷ (22,4 л/моль) = 0,714 г/л
Якщо х - мольна частка СО 2 і (1— х) - мольна частка CH 4, ми можемо записати
1,964 х + 0,714 (1—х) = 1,214
(Чи має це сенс? Зверніть увагу, що якщо х = 0, щільність буде чистим CH 4, тоді як якби це було 1, це було б чистим CO 2.)
Розширення вищевказаного рівняння і розв'язування для х дає мольні частки 0,40 для CO 2 і 0,60 для CH 4.
Висловлювання складу газової суміші
Оскільки більша частина обсягу, зайнятого газом, складається з порожнього простору, ніщо не заважає двом або більше видам газів займати однаковий об'єм. Однорідні суміші такого роду взагалі відомі як розчини, але до них прийнято відносити просто як газоподібні суміші. Вказати склад газоподібних сумішей можна різними способами, але найпоширеніші - за обсягами і за мольними фракціями.
Об'ємні фракції
З Закону Авогадро ми знаємо, що «рівні обсяги містять рівну кількість молекул». Це означає, що обсяги газів, на відміну від твердих речовин і рідин, є адитивними. Так що якщо перегороджена ємність має два об'єми газу А в одній секції і один моль газу В в іншій (обидва при однаковій температурі і тиску), а перегородку прибираємо, обсяг залишається незмінним.
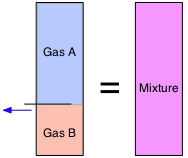
Об'ємні фракції часто називають частковими обсягами:
\[V_i = \dfrac{v_i}{\sum v_i}\]
Не дозволяйте цьому типу позначення відкласти вас! Знак підсумовування σ (грец. Sigma) просто означає скласти v (обсяги) кожного газу. Таким чином, якщо Газ А є речовиною "i -го», як у виразі безпосередньо вище, підсумовування проходить від i =1 до i =2. Зауважте, що ми можемо використовувати часткові обсяги для визначення складу суміші, навіть якщо вона ніколи не була зроблена шляхом об'єднання чистих газів.
Коли ми говоримо, що повітря, наприклад, становить 21 відсоток кисню та 78 відсотків азоту за обсягом, це те саме, що сказати, що ці самі відсотки молекул у повітрі складаються з O 2 та N 2. Аналогічно в 1,0 моль повітря знаходиться 0,21 моль O 2 і 0,78 моль N 2 (інший 0,1 моль складається з різних слідових газів, але в основному є неоном.) Зверніть увагу, що ви ніколи не могли припустити подібної еквівалентності з сумішами рідин або твердих речовин, до яких принцип E.V.E.N. не застосовується.
Дроби кротів
Ці два останні числа (0,21 і 0,78) також виражають мольні фракції кисню і азоту в повітрі. Моль фракція означає саме те, що вона говорить: фракція молекул, які складаються з конкретної речовини. Це виражається алгебраїчно
\[X_i = \dfrac{n_i}{\sum_i n_i}\]
так що у випадку кисню в повітрі його моль фракція
\[ X_{O_2} = \dfrac{n_{O_2}}{n_{O_2}+n_{N_2}+n_{Ar}}= \dfrac{0.21}{1}=0.21 \nonumber\]
Суміш\(O_2\) і закису азоту\(N_2O\), іноді використовується як м'який анестетик в стоматологічній хірургії. Певна суміш цих газів має щільність 1,482 г L —1 при 25 і 0,980 атм. Яким був моль-відсоток\(N_2O\) в цій суміші?
Рішення
Спочатку знайдіть щільність газу, яку мав би на STP:
\[\left(1.482 \mathrm{g} \mathrm{L}^{-1}\right) \times\left(\frac{298}{273}\right)\left(\frac{1}{980}\right)=1.65 \mathrm{g} \mathrm{L}^{-1}\nonumber \]
Молярна маса суміші становить (1,65 г Л —1) (22,4 л моль —1) = 37,0 г моль —1. Молекулярні маси\(O_2\) і\(N_2\) складають 32 і 44 відповідно. 37,0 дорівнює 5/12 різниці між молярними масами двох чистих газів. Оскільки щільність газової суміші прямо пропорційна її середній молярній масі, мольна частка важчого газу в суміші також становить 5/12:
\[\dfrac{37-32}{44-32}=\dfrac{5}{12}=0.42 \nonumber\]
Що таке мольна фракція вуглекислого газу в суміші, що складається з рівних мас СО 2 (MW=44) і неону (MW=20,2)?
Рішення
Припустимо будь-яку довільну масу, наприклад 100 г, знайдіть еквівалентні числа молів кожного газу, а потім підставляємо в визначення мольного дробу:
- n СО2 = (100 г) ÷ (44 г моль —1) = 2,3 моль
- n Ne = (100 г) ÷ (20,2 г моль —1) = 4,9 моль
- X Ne = (2,3 моль) ÷ (2,3 моль + 4,9 моль) = 0,32
Закон Дальтона парціальних тисків
Ідеальне рівняння стану газу застосовується до сумішей так само, як і до чистих газів. Саме з газовою сумішшю, звичайним повітрям Бойл, Гей-Люссак і Чарльз робили свої ранні експерименти. Єдина нова концепція, яка нам потрібна для того, щоб мати справу з газовими сумішами - парціальний тиск, концепція, придумана відомим англійським хіміком Джоном Далтоном (1766-1844). Дальтон міркував, що низька щільність і висока стисливість газів свідчить про те, що вони складаються здебільшого з порожнього простору; з цього випливає, що коли два і більше різних газів займають один і той же обсяг, вони поводяться цілком незалежно.
Внесок, який кожен компонент газоподібної суміші вносить у загальний тиск газу, відомий як парціальний тиск цього газу. Сам Далтон висловив цей закон простим і яскравим способом, показаним зліва.
Звичайний спосіб заявити Закон Дальтона про парціальний тиск є
Загальний тиск газу - це сума парціальних тисків його складових
який виражається алгебраїчно як
\[P_{total}=P_1+P_2+P_3 ... = \sum_i P_i\]
або, еквівалентно
\[ P_{total} = \dfrac{RT}{V} \sum_i n_i\]
Існує також подібний зв'язок, заснований на об'ємних частках, відомий як закон Амагата часткових обсягів. Він точно аналогічний закону Дальтона, в тому, що в ньому зазначено, що загальний обсяг суміші - це всього лише сума часткових обсягів її компонентів. Але є дві важливі відмінності: закон Амагата діє лише для ідеальних газів, які повинні бути з однаковою температурою та тиском. Закон Дальтона не має жодного з цих обмежень. Хоча закон Амагата здається інтуїтивно очевидним, він іноді виявляється корисним у застосуваннях хімічної інженерії. Ми не будемо використовувати його в цьому курсі.
Розрахуйте масу кожного компонента, присутнього в суміші фтору (МВт) і ксенону (МВт 131,3), що міститься в 2,0-літрової колбі. Парціальний тиск становить 350 мм.рт.ст, а загальний тиск - 724 мм.рт.ст при 25°C.
Рішення
З закону Дальтона парціальний тиск F 2 дорівнює (724 — 350) = 374 торр:
Фракції кротів
\[\chi_{Xe} = \dfrac{350}{724} = 0.48 \nonumber\]
і
\[\chi_{F_2} = \dfrac{374}{724} = 0.52 \nonumber\]
Загальна кількість молів газу становить
\[n=\dfrac{P V}{R T}=\frac{(724 / 60)(2)}{(.082)(298)}=0.078 \mathrm{mol}\nonumber\]
Маса\(Xe\) є
\[(131.3\, g\, mol^{–1}) \times (0.48 \times 0.078\, mol) = 4.9\, g \nonumber\]
Три колби, що мають різні обсяги і містять різні гази при різному тиску, з'єднані запірними кранами, як показано на малюнку. Коли запірні крани відкриваються,
- Яким буде тиск в системі?
- Який газ буде найбільш рясний в суміші?
Припустимо, що температура рівномірна і що обсяг сполучних трубок мізерно малий.
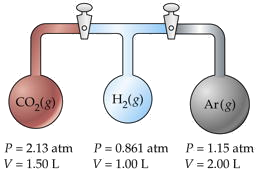
Рішення
Хитрість тут полягає в тому, щоб відзначити, що загальна кількість молів n T і температура залишаються незмінними, тому ми можемо використовувати закон Бойла PV = постійний. Опрацюємо деталі тільки для СО 2, позначаються індексами а.
Для СО 2,
П а В а = (2,13 атм) (1,50 л) = 3,19 л-атм.
Додаючи фотоелектричні продукти для кожного окремого контейнера, отримуємо
\[\sum P_iV_i = 6.36 L-atm = n_T RT. \nonumber\]
Цю суму ми будемо називати Р 1 В 1. Після відкриття запірних кранів і змішання газів нові умови позначають П 2 В 2.
З закону Бойля,
= 6,36 л атм. V 2 = σ В i = 4,50 Л.Розв'язуючи для кінцевого тиску Р 2 отримуємо
(6,36 л атм)/(4,50 л) = 1,41 атм.
Для СО 2 це працює до (3,19/ РТ)/(6,36/ РТ) = 0,501. Оскільки це перевищує 0,5, ми знаємо, що це найпоширеніший газ у кінцевій суміші.
Застосування закону Дальтона: Збір газів над водою
Поширеним лабораторним методом збору газоподібного продукту хімічної реакції є проведення його в перевернуту трубку або пляшку, наповнену водою, отвір якої занурюють в більшу ємність з водою. Таке розташування називається пневматичним жолобом, і широко використовувалося в перші часи хімії. Коли газ надходить у пляшку, він витісняє воду і потрапляє в пастку у верхній частині.
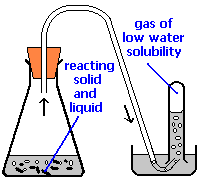
Обсяг газу можна спостерігати за допомогою каліброваної шкали на балоні, але як щодо його тиску? Загальний тиск, що обмежує газ, - це саме тиск атмосфери, що передає свою силу через воду. (Точний розрахунок також повинен був би враховувати висоту водяного стовпа в перевернутій трубі.) Але сама рідка вода завжди знаходиться в рівновазі зі своєю парою, тому простір у верхній частині трубки являє собою суміш двох газів: газу, що збирається, і газоподібного Н 2 О. Парціальний тиск Н 2 О відомий як тиск пари води і воно залежить від температури. Для того, щоб визначити кількість газу, який ми зібрали, ми повинні використовувати Закон Дальтона, щоб знайти парціальний тиск цього газу.
Кисневий газ був зібраний над водою, як показано вище. Атмосферний тиск було 754 мм.рт.ст, температура 22°C, а об'єм газу 155 мл. Тиск пари води при 22° C становить 19,8 торр. Використовуйте цю інформацію для оцінки кількості\(O_2\) вироблених родимок.
Рішення
З закону Далтона,\(P_{O_2} = P_{total} – P_{H_2O} = 754 – 19.8 = 734 \; torr = 0.966\; atm\).
\[n=\frac{P V}{R T}=\frac{0.966 \mathrm{atm} \times(0.155 \mathrm{L})}{\left(.082 \mathrm{L} \mathrm{atm} \mathrm{mol}^{-1} \mathrm{K}^{-1}\right)(295 \mathrm{K})}=.00619 \mathrm{mol}\nonumber\]
Застосування закону Далтона: підводне плавання
Наші дихальні системи призначені для підтримки належної концентрації кисню в крові, коли парціальний тиск O 2 становить 0,21 атм, його нормальне значення рівня моря. Нижче поверхні води тиск збільшується на 1 атм за кожне збільшення глибини на 10,3 м; таким чином аквалангіст на 10,3 м відчуває в цілому тиск 2 атм, що тисне на тіло. Для того, щоб легені не руйнувалися, повітря, яким дихає дайвер, також повинен бути приблизно під таким же тиском.
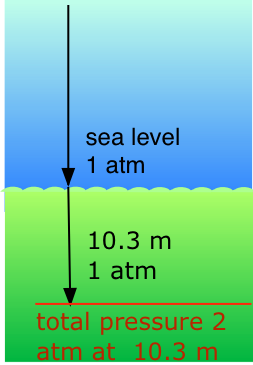
Але при загальному тиску в 2 атм парціальний тиск\(O_2\) в звичайному повітрі становило б 0,42 атм; на глибині 100 футів (близько 30 м)\(O_2\) тиск 0,8 атм було б занадто високим для здоров'я. З цієї причини повітряна суміш у резервуарах під тиском, які носять аквалангісти, повинна містити меншу частку\(O_2\). Цього можна досягти найбільш просто шляхом підвищення вмісту азоту, але високий парціальний тиск N 2 також може бути небезпечним, що призводить до стану, відомого як наркоз азоту. Кращим розріджувачем для стійкого глибокого занурення є гелій, який має дуже незначну схильність до розчинення в крові навіть при високому тиску.
