8.11: Парціальний тиск і закон Далтона

Ідеальний закон газу також може бути перебудований, щоб показати, що тиск газу пропорційний кількості газу:

$$P=\frac{RT}{V}\,n\label{1}$$

Таким чином, коефіцієнт RT/V може бути використаний для перетворення кількості речовини та тиску в контейнері заданого об'єму та температури.

Рівняння також$\ref{1}$ корисно в роботі з ситуацією, коли два або більше газів обмежені в одному контейнері (тобто однаковому об'ємі). Припустимо, наприклад, що у нас було 0,010 моль газу в 250-мл контейнері при температурі 32°С.

$$\begin{align}P & =\frac{RT}{V}\,n =\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.010 mol}\\ & =\text{1}\text{.00 atm}\end{align} \nonumber$$

Тепер припустимо, що ми наповнили ту ж ємність 0,004 моль Н ₂ (г) при тій же температурі. Тиск був би

$$\begin{align}p_{\text{H}_{\text{2}}} & =\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.004 mol}\\ & =\text{0}\text{.40 atm}\end{align} \nonumber$$

Якщо покласти 0,006 моль N ₂ в ємність,

$$p_{\text{N}_{\text{2}}}=\frac{\text{0}\text{.0820 liter atm mol}^{-\text{1}}\text{ K}^{-\text{1}}\,\times \text{ 305 K}}{\text{0}\text{.250 liter}}\,\times \text{ 0}\text{.006 mol}=\text{0}\text{.60 atm} \nonumber$$

Тепер припустимо, що ми поміщаємо як 0,004 моль H ₂, так і 0,006 моль N ₂ в ту ж колбу разом. Яким би був тиск? Оскільки ідеальний закон газу залежить не від того, який газ у нас є, а лише від кількості будь-якого газу, тиск (0,004 + 0,006) моль, або 0,010 моль, було б саме тим, що ми отримали в нашому першому розрахунку. Але це лише сума тиску, яке H ₂ чинив би, якби він зайняв один контейнер плюс тиск N ₂, якби це був єдиний присутній газ. Тобто,

$$P_{total} = p_{\text{H}_{2}} + p_{\text{N}_{2}} \nonumber$$

На малюнку нижче показано поняття парціального тиску більш конкретно, показуючи тиск кожного газу окремо в контейнері, а потім показуючи комбінований тиск газів після змішування.

Малюнок$\PageIndex{1}$: Вище на малюнку показано, як працює закон Дальтона парціального тиску. Поодинці Водень має тиск 0,4 атм, в той час як Азот має тиск 0,6 атм. При розміщенні в одній ємності загальний тиск становить 1 атм, при цьому кожен газ вносить свій парціальний тиск. Зображення кредитів: OpenStax коледж

Ми щойно розробили приклад закону Далтона парціального тиску (названий на честь Джона Далтона, його першовідкривача). Цей закон говорить, що в суміші двох і більше газів загальний тиск - це сума парціальних тисків всіх складових. Парціальний тиск газу - це тиск, який буде чинити газ, якби він зайняв контейнер сам по собі. Парціальний тиск представлено малої літерою р.

Закон Дальтона парціальних тисків найчастіше зустрічається, коли газ збирається шляхом витіснення води, як показано на малюнку 2.

Малюнок$\PageIndex{2}$: Загальний тиск, що чиниться вологим газом, дорівнює сумі парціального тиску самого газу + тиску пари води при цій температурі. (При 20° C тиск пари води становить 17,3 мм рт.ст.)

Ілюстрація тонкої вузької труби занурений у воду і подається в нижній частині вимірювальної трубки. Бульбашки видно, що виходять з гирла трубки.

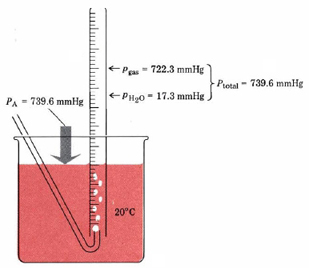
Оскільки газ прокинувся через воду, він містить деякі молекули води і, як кажуть, «мокрий». Загальний тиск цього мокрого газу - це сума парціального тиску самого газу і парціального тиску водяної пари, яку він містить. Останнє парціальний тиск називається тиском пари води. Це залежить тільки від температури експерименту і може бути отримано з довідника або з таблиці 1.

ТАБЛИЦЯ$\PageIndex{1}$: Тиск пари води в залежності від температури.

Температура (°C)	Тиск пари (мм рт.ст.)	Тиск пари (кПа)
0	4.6	0,61
5	6.5	0,87
10	9.2	1.23
15	12.8	1.71
20	17.5	2.33
25	23.8	3.17
30	31.8	4.24
50	92.5	12.33
70	233.7	31.16
75	289.1	38.63
80	355.1	47.34
85	433.6	57.81
90	525.8	70.10
95	633.9	84.51
100	760.0	101.32

Приклад$\PageIndex{1}$: Volume of Hydrogen

Припустимо, 0,321 г металу цинку дозволяється вступати в реакцію з надлишком соляної кислоти (водний розчин газу HCl) за рівнянням

$$\text{Zn} (s) + 2 \text{HCL} (aq) \rightarrow \text{Zn} \text{Cl}_{2} (aq) + \text{H}_{2} (g) \nonumber$$

Отриманий водневий газ збирається над водою при 25° C, тоді як барометричний тиск становить 745,4 мм рт.ст. Який обсяг вологого водню буде збиратися?

Розчин З табл. 1 знаходимо, що при 25°C тиск пари води становить 23,8 мм рт. ст. Відповідно

р _{Н 2} = р _{загальна} — р _{Н 2 О} = 754 мм рт.ст. — 23,8 мм рт.ст. = 721,6 мм рт. ст.

Це повинно бути перетворено на одиниці, сумісні R:

$$p_{\text{H}_{\text{2}}}=\text{721}\text{.6 mmHg }\times \,\frac{\text{1 atm}}{\text{760 mmHg}}=\text{0}\text{.949 atm} \nonumber$$

Дорожня карта для цієї проблеми є

$$m_{\text{Zn}}\xrightarrow{M_{\text{Zn}}}n_{\text{Zn}}\xrightarrow{S\left( \text{H}_{\text{2}}\text{/Zn} \right)}n_{\text{H}_{\text{2}}}\xrightarrow{RT/P}V_{\text{H}_{\text{2}}} \nonumber$$

Таким чином

$$\begin{align}V_{\text{H}_{\text{2}}} & =\text{0}\text{.321 g Zn }\times \,\frac{\text{1 mol Zn}}{\text{65}\text{.38 g Zn}}\,\times \,\frac{\text{1 mol H}_{\text{2}}}{\text{2 mol Zn}}\,\times \,\frac{\text{0}\text{.0820 liter atm}}{\text{1 K mol H}_{\text{2}}}\,\times \,\frac{\text{293}\text{0.15 K}}{\text{0}\text{.987 atm}}\\ & =\text{0}\text{.126 liter}\end{align} \nonumber$$