4.3: Оптимізація

Часткові похідні розповідають нам щось про те, де поверхня має локальні максимуми та мінімуми. Пам'ятайте, що навіть в однозмінних випадках були критичні точки, які не були ні максимумами, ні мінімумами — це також справедливо для функцій багатьох змінних. Насправді, як і слід було очікувати, ситуація ще складніше.

Другі похідні

Коли ви знайдете часткову похідну функції двох змінних, ви отримуєте ще одну функцію з двох змінних — ви також можете взяти її часткові похідні. Ми робили це раніше, в налаштуваннях однієї змінної. У однозмінній налаштуванні друга похідна давала інформацію про те, як граф був вигнутий. У налаштуванні з двома змінними другі часткові похідні дають деяку інформацію про те, як поверхня вигнута, коли ви подорожуєте по поперечних перерізах - але це не дуже повна інформація про всю поверхню.

Уявіть, що у вас є поверхня, яка скуйовджену навколо точки, як те, що відбувається біля кнопки на переповненому дивані, або затиснутий шматок тканини, або зморшкувата шкіра біля великого пальця, коли ви робите кулак. Прямо в цей момент, у кожному напрямку ви рухаєтесь, станеться щось інше - воно може збільшуватися, зменшуватися, кривитися вгору, кривою вниз... Проста фраза, як увігнута вгору або увігнута вниз, не може описати все, що може статися на поверхні.

Як не дивно, однак, існує ще другий тест похідних, який може допомогти вам вирішити, чи є точка локальним максимумом або мінімальним чи ні, тому ми все ще хочемо знайти другі похідні.

Другі часткові похідні

Припустимо$f(x,y)$ is a function of two variables. Then it has four другі часткові похідні: $$\begin{align*} f_{xx} & = \frac{\partial}{\partial x}\left(f_x\right)=\left(f_x\right)_x & f_{xy} & = \frac{\partial}{\partial y}\left(f_x\right)=\left(f_x\right)_y\\ f_{yx} & = \frac{\partial}{\partial x}\left(f_y\right)=\left(f_y\right)_x & f_{yy} & = \frac{\partial}{\partial y}\left(f_y\right)=\left(f_y\right)_y \end{align*} \nonumber$$ $f_{xy}$ and $f_{yx}$ are called the змішані (другі) часткові похідні$f$.

Позначення Лейбніца для другої часткової похідної трохи заплутано, і ми не будемо використовувати його так часто: $$\begin{align*} f_{xx} & = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2 f}{\partial x^2} & f_{xy} & = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2 f}{\partial y \partial x}\\ f_{yx} & = \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2 f}{\partial x \partial y} & f_{yy} & = \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2 f}{\partial y^2} \end{align*} \nonumber$$

Зверніть увагу, що порядок змінних для змішаних часткових йде справа наліво в позначенні Лейбніца замість зліва направо.

Приклад$\PageIndex{1}$

Знайдіть всі чотири часткові похідні$f(x,y)=x^2-4xy+4y^2$.

Рішення

Ми повинні почати з пошуку (перших) часткових похідних: $$\begin{align*} f_x(x,y) & = 2x-4y \\ f_y(x,y) & = -4x+8y \end{align*} \nonumber$$

Тепер ми готові взяти другі часткові похідні: $$\begin{align*} f_{xx}(x,y) & = \frac{\partial}{\partial x}(2x-4y)=2 \\ f_{xy}(x,y) & = \frac{\partial}{\partial y}(2x-4y)=-4 \\ f_{yx}(x,y) & = \frac{\partial}{\partial x}(-4x+8y)=-4 \\ f_{yy}(x,y) & = \frac{\partial}{\partial y}(-4x+8y)=8 \end{align*} \nonumber$$

Можливо, ви помітили, що дві змішані часткові похідні були рівними в цьому останньому прикладі. Виявляється, це не випадковість — це теорема!

Теорема про змішані часткові похід

Якщо$f$, $f_x$, $f_y$, $f_{xy}$, and $f_{yx}$ are all continuous (no breaks in their graphs), then $$f_{xy}=f_{yx}. \nonumber$$

Насправді, поки$f$ і всі його відповідні часткові похідні є неперервними, змішані частки рівні, навіть якщо вони більш високого порядку, і навіть якщо функція має більше двох змінних.

Ця теорема означає, що заплутані позначення Лейбніца для другої похідної не є великою проблемою - майже в кожній ситуації змішані частки рівні, тому порядок, в якому ми їх обчислюємо, не має значення.

Приклад$\PageIndex{2}$

Знайти$\frac{\partial^2 f}{\partial x \partial y}$ для$f(x,y)=\frac{e^{x+y}}{y^3+y}+y\ln(y)$.

Рішення

Перші часткові похідні ми вже знайшли в попередньому прикладі: $$\begin{align*} \frac{\partial f}{\partial x} & = \frac{1}{y^3+y}e^{x+y} \\ \frac{\partial f}{\partial y} & = \frac{\left( e^{x+y}(1) \right)\left( y^3+y \right)-\left( e^{x+y} \right)\left( 3y^2+1 \right)}{\left( y^3+y \right)^2}+\left( 1 \right)\left( \ln(y) \right)+\left( y \right)\left( \frac{1}{y} \right) \end{align*} \nonumber$$

Тепер нам потрібно знайти змішану часткову похідну. Теорема говорить$\frac{\partial f^2}{\partial x \partial y}=\frac{\partial f^2}{\partial y \partial x}$, що, тому не має значення, чи знайдемо ми часткову похідну щодо$y$ або часткову$\frac{\partial f}{\partial y}$ похідну щодо$x$.$\frac{\partial f}{\partial x}$ Що б ви хотіли зробити?

Схоже, буде простіше обчислити змішану часткову, знайшовши часткову похідну щодо$y$ - вона все ще виглядає$\frac{\partial f}{\partial x}= \frac{1}{y^3+y}e^{x+y}$ брудною, але виглядає менш безладно: $$\frac{\partial f^2}{\partial y \partial x}= \frac{\partial}{\partial y}\left(\frac{1}{y^3+y}e^{x+y}\right)=\frac{\left(e^{x+y}\right)\left(y^3+y\right)-\left(e^{x+y}\right)\left(3y^2+1\right)}{\left(y^3+y\right)^2} \nonumber$$

Якби ми вирішили зробити це іншим способом, ми б опинилися в тому ж місці. Врешті-решт...

Локальні максимуми, локальні мінімуми та точки сідла

Давайте коротко розглянемо задачі max-min в одній змінній.

Локальний макс - це точка на кривій, яка вище всіх сусідніх точок. Місцевий хв нижче всіх довколишніх точок. Ми знаємо, що локальний max або min може відбуватися тільки в критичних точках, де похідна дорівнює нулю або невизначена. Але ми також знаємо, що не всі критичні точки є макс або хв, тому нам також потрібно перевірити їх за допомогою першого похідного або другого похідного тесту.

Ситуація з функцією двох змінних багато в чому однакова. Так само, як і в випадку з однією змінною, першим кроком є пошук критичних точок, місць, де обидві часткові похідні або нульові, або невизначені.

Визначення: Локальний максимум і Мінімум

• $f$має локальний максимум,$(a, b)$ якщо$f(a, b) \geq f(x, y)$ для всіх точок$(x, y)$ поблизу$(a, b)$.
• $f$має локальний мінімум,$(a, b)$ якщо$f(a, b) \leq f(x, y)$ для всіх точок$(x, y)$ поблизу$(a, b)$.

Критичною точкою для функції$f(x, y)$ є точка$(x, y)$ (або$(x, y, f(x, y))$), де обидва наступні є істинними:

1. $f_x=0$або не визначено, і
2. $f_y=0$або не визначено.

Так само, як і в випадку з однією змінною, локальний макс або хв$f$ може відбуватися лише в критичній точці.

Так само, як і в налаштуванні однієї змінної, не всі критичні точки є локальними max або min. Для функції двох змінних критичною точкою може бути локальний max, локальний min або точка сідла.

Точка на поверхні є локальним максимумом, якщо вона вища за всі точки поблизу; точка є локальним мінімумом, якщо вона нижча за всі точки поблизу.

Точка сідла - це точка на поверхні, яка є мінімумом на деяких шляхах і максимумом уздовж деяких інших. Це називається так, тому що він має форму трохи як сідло, яке ви могли б використовувати для їзди на коні. Ви можете побачити точку сідла, зробивши кулак - між кісточками вказівного та середнього пальців ви можете побачити місце, яке є мінімальним, коли ви йдете через кісточки, але максимум, коли ви йдете вздовж вашої руки до пальців.

Ось зображення точки сідла з декількох різних кутів. Це поверхня$f(x,y)=5x^2-3y^2+10$, і над початком є точка сідла. Лінії показують, як виглядає поверхня над осями$x$ - і$y$ -. Зверніть увагу, як точка над початком, де лінії перетинаються, є локальним мінімумом в одному напрямку, але локальним максимумом в іншому напрямку.

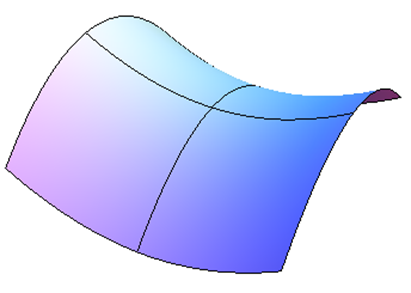
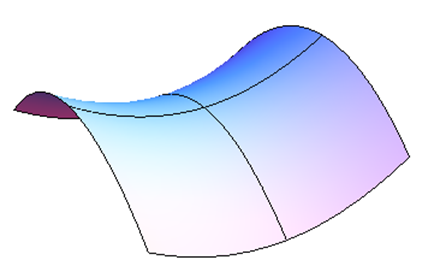
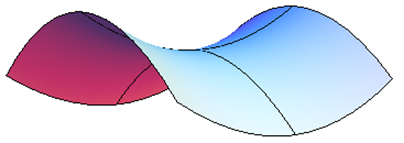
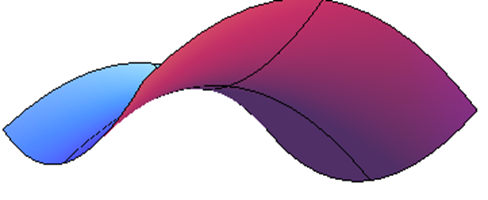
Другий похідний тест

Так само, як і в випадку з однією змінною, нам знадобиться спосіб перевірити критичні точки, щоб побачити, чи є вони локальними max або min. Існує другий тест похідних для функцій двох змінних, який може допомогти, але, як і в випадку з однією змінною, він не завжди дасть відповідь.

Другий тест похідних для функцій двох змінних

1. Знайти всі критичні точки$f(x,y)$.
2. Обчислити $$D(x,y)=\left(f_{xx}\right)\left(f_{yy}\right)-\left(f_{xy}\right)\left(f_{yx}\right),\nonumber$$ і оцінити його в кожній критичній точці.
   1. Якщо$D \gt 0$, то$f$ має локальний max або min в критичній точці. Щоб побачити який, подивіться на знак$f_{xx}$:
      • Якщо$f_{xx}\gt 0$, то$f$ має локальний мінімум в критичній точці.
      • Якщо$f_{xx}\lt 0$, то$f$ має локальний максимум в критичній точці.
   2. Якщо$D \lt 0$ потім$f$ має сідлову точку в критичній точці.
   3. Якщо$D = 0$, може бути локальний max, локальний min, або ні (тобто тест непереконливий).

Приклад$\PageIndex{3}$

Знайти всі локальні максимуми, мінімуми та точки сідла для функції $$f(x,y)=x^3+y^3+3x^2-3y^2-8. \nonumber$$

Рішення

Для початку нам знадобляться часткові похідні:$f_x=3x^2+6x$ і$f_y=3y^2-6y$.

Критичні точки - це місця, де обидва вони дорівнюють нулю (жодна з них ніколи не визначена):$f_x=3x^2+6x=3x(x+2)=0$ коли$x = 0$ чи коли$x = -2$. $f_y=3y^2-6y=3y(y-2)=0$коли$y = 0$ або коли$y = 2$.

Зібравши їх разом, отримуємо чотири критичні точки: (0, 0), (-2, 0), (0, 2) і (-2, 2).

Тепер, щоб класифікувати їх, ми будемо використовувати другий похідний тест. Нам знадобляться всі другі часткові похідні: $$f_{xx}=6x+6,\ f_{yy}=6y-6,\ f_{xy}=f_{yx}=0.\nonumber$$

Тоді $$D(x,y)=(6x+6)(6y-6)-(0)(0)=(6x+6)(6y-6). \nonumber$$

Тепер подивіться на кожну критичну точку по черзі:

• В (0, 0):$D(0,0)=(6(0)+6)(6(0)-6)=(6)(-6)=-36 \lt 0$, Таким чином, є точка сідла в (0, 0).
• При (-2, 0):$D(-2,0)=(6(-2)+6)(6(0)-6)=(-6)(-6)=36 \gt 0$ і$f_{xx}(-2,0)=6(-2)+6=-6 \lt 0$, так є локальний максимум при (-2, 0).
• В (0, 2):$D(0,2)=(6(0)+6)(6(2)-6)=(6)(6)=36 \gt 0$ і$f_{xx}(0,2)=6(0)+6=6 \gt 0$, таким чином, існує локальний мінімум на (0, 2).
• В (-2, 2):$D(-2,2)=(6(-2)+6)(6(2)-6)=(-6)(6)=-36 \lt 0$, Отже, є ще одна точка сідла на (-2, 2).

Приклад$\PageIndex{4}$

Знайти всі локальні максимуми, мінімуми та точки сідла для функції $$z=9x^3+\frac{y^3}{3}-4xy. \nonumber$$

Рішення

Нам знадобляться всі часткові похідні та другі часткові похідні, тому давайте обчислимо їх все спочатку: $$\begin{align*} z_x & = 27x^2-4y,\quad z_y= y^2-4x,\\ z_{xx} & = 54x,\quad z_{xy}=z_{yx}= -4,\quad z_{y}= 2y. \end{align*} \nonumber$$

Тепер, щоб знайти критичні точки: Нам потрібно обидві$z_x$ і$z_y$ бути нульовими (жодна з них ніколи не визначена), тому нам потрібно вирішити цей набір рівнянь одночасно: $$\begin{align*} z_x & = 27x^2-4y=0 \\ z_y & = y^2-4x=0 \end{align*} \nonumber$$

Можливо, минув деякий час, як ви вирішували системи рівнянь. Одним з методів розв'язку є метод заміщення — вирішити одне рівняння для однієї змінної і підставити в інше рівняння:\[ \left.\begin{align*} 27x^2-4y & = 0 \\ y^2-4x & = 0 \end{align*}\right\} \to \text{Solve $y^2-4x=0$ for $x=\frac{y^2}{4}$ $\dots$} \nonumber \]... потім підставити в інше рівняння: $$\begin{align*} 27\left(\frac{y^2}{4}\right)^2-4y & = 0 \\ \frac{27}{16}y^4-y & = 0 \end{align*} \nonumber$$

Тепер у нас є лише одне рівняння в одній змінній для вирішення. Факторинг$y$ дає $$y\left(\frac{27}{16}y^3-1\right)=0, \nonumber$$ так$y=0$ або$\frac{27}{16}y^3-1=0$, даючи$y=\sqrt[3]{\frac{1}{27/16}}=\frac{\sqrt[3]{4}}{3}$.

Підключення до рівняння,$x=\frac{y^2}{4}$ щоб знайти,$x$ дає нам дві критичні точки: (0,0) і$\left(\frac{4}{9},\frac{4}{3}\right)$.

Тепер протестуємо їх. Спочатку обчислити $$\begin{align*} D(x,y) & = (f_{xx})(f_{yy})-(f_{xy})(f_{yx}) \\ & = (54x)(2y)-(-4)(-4) \\ & = 108xy-16 \end{align*} \nonumber$$ Потім оцінити$D$ в двох критичних точках:

• В (0,0):$D(0,0) = -16 \lt 0$, Таким чином, є точка сідла в (0, 0).
• За адресою$\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right)$:$D\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right) =16(\sqrt[3]{4}-1) \gt 0$, і$f_{xx}\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right) \gt 0$, значить, є локальний мінімум на$\left(\frac{4}{9},\frac{\sqrt[3]{4}}{3}\right)$.

Прикладна оптимізація

Приклад$\PageIndex{5}$

Компанія виробляє два продукти. Рівняння попиту для двох продуктів наведені нижче. $p_1$,$p_2$,$q_1$, і$q_2$ є ціни та кількості для Продукції 1 і 2. $$\begin{align*} q_1 & = 200-3p_1-p_2 \\ q_2 & = 150-p_1-2p_2 \end{align*} \nonumber$$

Рішення

Знайдіть ціну, яку компанія повинна стягувати за кожен товар, щоб максимізувати загальний дохід. Що таке максимальний дохід?

Виручка все ще цінова$\cdot$ кількість. Якщо ми продаємо два продукти, то загальний дохід буде сумою доходів від двох продуктів: $$\begin{align*} R(p_1,p_2) & = p_1q_1+p_2q_2 \\ & = p_1(200-3p_1-p_2)+p_2(150-p_1-2p_2) \\ & = 200p_1-3p_1^2-2p_1p_2+150p_2-2p_2^2 \end{align*} \nonumber$$

Це функція двох змінних, двох цін, і нам потрібно оптимізувати її (так само, як і в попередніх прикладах). Спочатку знаходимо критичні точки. Позначення тут стає трохи важко дивитися, але повісити там - це те саме, що ми робили раніше. $$R_{p_1}=200-6p_1-2p_2 \ \text{ and } \ R_{p_2}=150-2p_1-4p_2. \nonumber$$

Рішення їх одночасно дає одну критичну точку$(p_1, p_2)=(25,25)$

Щоб підтвердити, що це дає максимальний дохід, нам потрібно використовувати Second Derivative Test. Знайдіть всі другі похідні: $$R_{p_1 p_2}=-6,\ R_{p_2 p_2}=-4,\ \text{ and }\ R_{p_1 p_2}=R_{p_2 p_1}=-2. \nonumber$$

Так$D(25,25)=(-6)(-4)-(-2)(-2) \gt 0$ і$R_{p_1 p_2}(25,25) \lt 0$, так це дійсно локальний максимум.

Таким чином, для максимізації доходу компанія повинна стягувати 25 доларів за одиницю за обидва продукти. Це дасть максимальний дохід у розмірі 4375 доларів.