14.3: Часткові похідні

Цілі навчання

• Обчисліть часткові похідні функції двох змінних.
• Обчисліть часткові похідні функції більше двох змінних.
• Визначте похідні вищого порядку функції двох змінних.
• Поясніть значення рівняння з частинними похідними і наведіть приклад.

Тепер, коли ми розглянули межі і неперервність функцій двох змінних, можна приступати до вивчення похідних. Пошук похідних функцій двох змінних є ключовим поняттям у цій главі, з такою кількістю застосувань у математиці, науці та техніці, як диференціація однозмінних функцій. Однак ми вже бачили, що межі та безперервність багатоваріантних функцій мають нові проблеми і вимагають нової термінології та ідей для їх вирішення. Це також переходить у диференціацію.

Похідні функції двох змінних

При вивченні похідних функцій однієї змінної виявлено, що однією інтерпретацією похідної є миттєва швидкість зміни$y$ як функції позначення$x.$ Лейбніца для похідної є,$dy/dx,$ що означає, що$y$ є залежною змінною і$x$ незалежна змінна. Для функції$z=f(x,y)$ з двох змінних,$x$ і$y$ є незалежними змінними і$z$ є залежною змінною. Це викликає відразу два питання: Як ми адаптуємо позначення Лейбніца для функцій двох змінних? Крім того, що таке тлумачення похідної? Відповідь криється в часткових похідних.

Визначення: Часткові похідні

$f(x,y)$Дозволяти бути функцією двох змінних. Тоді часткова$f$ похідна щодо$x$, написана як$∂f/∂x,$, або$f_x,$ визначається як

$$\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1}$$

Часткова$f$ похідна щодо$y$, написана як$∂f/∂y$, або$f_y,$ визначається як

$$\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2}$$

Це визначення показує вже дві відмінності. По-перше, змінюється позначення, в тому сенсі, що ми все ще використовуємо версію позначення Лейбніца, але$d$ в оригінальному позначенні замінюється символом$∂$. (Цей округлий зазвичай$“d”$ називають «частковим», тому$∂f/∂x$ говорять як «часткове щодо»$x$.)$f$ Це перший натяк на те, що ми маємо справу з частковими похідними. По-друге, тепер у нас є дві різні похідні, які ми можемо взяти, оскільки є дві різні незалежні змінні. Залежно від того, яку змінну ми виберемо, ми можемо придумати різні часткові похідні взагалі, і часто робити.

Приклад$\PageIndex{1}$: Calculating Partial Derivatives from the Definition

Використовувати визначення часткової похідної як межі для обчислення$∂f/∂x$ та$∂f/∂y$ для функції

$$f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber$$

Рішення

Спочатку розрахуйте$f(x+h,y).$

$$\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \nonumber$$

Далі підставляємо це в Equation\ ref {pd1} і спрощуємо:

\ [\ почати {вирівнювати*}\ dfrac {f} {x} &=\ lim_ {h→0}\ dfrac {f (x+h, y) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2+2xh+h^2−3хy−2y^2y^2y^2−4x−−−4h+5y−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2+2h+h^2−3xy−3hy−2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y^2y −5y+12} {h}\
&=\ lim_ {h→0}\ dfrac {2 xh+h^2−3hy−4h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (2x+h−3y−4)} {h}\\
&=\ lim_ {h→0} (2x+h−3y−4)\\
&= 2x−3y−4. \ end {вирівнювати*}\]

Для розрахунку спочатку$\dfrac{∂f}{∂y}$ розрахуйте$f(x,y+h):$

$$\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}$$

Далі підставляємо це в Equation\ ref {pd2} і спрощуємо:

\ [\ почати {вирівнювати*}\ dfrac {f} {y} &=\ lim_ {h→0}\ dfrac {f (x, y+h) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2−3xy−3xh+2y^2y^2y^2h+2h^2h 4x+5y+5h−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2−3xy−3xh+2y^2y^2h+2h^2h ^2−4h+5y+5y+5y+5h−12x^2xy-2y^2y^2y^2h^2y^2h+2h^2h^2h^2h^2h+2h^2h^2h^2h^2+4x−5y+12} {h}\\
&=\ lim_ {h→0}\ dfrac {−3xh+4yh+2h^2+5h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (−3x+4y+2h+5)} {h}\\
&=\ lim_ {h→0} (−3x+4y+2h+5)\\
&= 3x+4y+4y+5\}\]

Вправа$\PageIndex{1}$

Використовувати визначення часткової похідної як межі для обчислення$∂f/∂x$ та$∂f/∂y$ для функції

$$f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber$$

Підказка

Використовуйте рівняння\ ref {pd1} та\ ref {pd2} з визначення частинних похідних.

Відповідь

$\dfrac{∂f}{∂x}=8x+2y+3$

$\dfrac{∂f}{∂y}=2x−2y−2$

Ідея, яку слід пам'ятати при обчисленні часткових похідних, полягає в тому, щоб розглядати всі незалежні змінні, крім змінної, щодо якої ми диференціюємо, як константи. Потім приступайте до диференціації як з функцією однієї змінної. Щоб зрозуміти, чому це правда, спочатку виправте$y$ та визначте$g(x)=f(x,y)$ як функцію$x$. Тоді

$$\begin{align*} g′(x) &=\lim_{h→0}\dfrac{g(x+h)−g(x)}{h} \\[6pt] &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\[6pt] &=\dfrac{∂f}{∂x}. \end{align*}$$

Те ж саме справедливо і для обчислення часткової$f$ похідної по відношенню до$y$. Цього разу зафіксуйте$x$ і визначте$h(y)=f(x,y)$ як функцію$y$. Тоді

$$\begin{align*} h′(x) &=\lim_{k→0}\dfrac{h(x+k)−h(x)}{k} \\[6pt] &=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k} \\[6pt] &=\dfrac{∂f}{∂y}. \end{align*}$$

Застосовуються всі правила диференціації.

Приклад$\PageIndex{2}$: Calculating Partial Derivatives

Обчисліть$∂f/∂x$ і$∂f/∂y$ для наступних функцій, утримуючи протилежну змінну постійну, потім диференціюючи:

1. $f(x,y)=x^2−3xy+2y^2−4x+5y−12$
2. $g(x,y)=\sin(x^2y−2x+4)$

Рішення:

а. для обчислення$∂f/∂x$ розглядайте змінну$y$ як константу. Потім$f(x,y)$ диференціюйте щодо$x$ використання суми, різниці та правил влади:

$$\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}$$

Похідні третього, п'ятого та шостого членів є нульовими, оскільки вони не містять змінної$x$, тому вони розглядаються як постійні терміни. Похідна від другого члена дорівнює коефіцієнту$x$, який є$−3y$. Обчислення$∂f/∂y$:

$$\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \nonumber$$

Це ті самі відповіді, отримані в прикладі$\PageIndex{1}$.

б. для обчислення$∂g/∂x,$ розглядати змінну y як константу. Потім$g(x,y)$ диференціюйте щодо$x$ використання правила ланцюга та правила влади:

$$\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}$$

Для обчислення$∂g/∂y,$ трактуйте змінну$x$ як константу. Потім$g(x,y)$ диференціюйте щодо$y$ використання правила ланцюга та правила влади:

$$\begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \nonumber$$

Вправа$\PageIndex{2}$

Розрахувати$∂f/∂x$ і$∂f/∂y$ для функції

$$f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber$$

утримуючи протилежну змінну постійну, потім диференціюючи.

Підказка

Використовуйте рівняння\ ref {pd1} та\ ref {pd1} з визначення частинних похідних.

Відповідь

$\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)$

$\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)$

Як ми можемо інтерпретувати ці часткові похідні? Нагадаємо, що графік функції двох змінних є поверхнею в$R^3$. Якщо зняти межу з визначення часткової похідної щодо$x$, то різницевий коефіцієнт залишається:

$$\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber$$

Це нагадує різницевий коефіцієнт для похідної функції однієї змінної, за винятком наявності$y$ змінної. Малюнок$\PageIndex{1}$ ілюструє поверхню, описану довільною функцією$z=f(x,y).$

Малюнок$\PageIndex{1}$: Січна лінія, що проходить через точки$(x,y,f(x,y))$ і$(x+h,y,f(x+h,y)).$

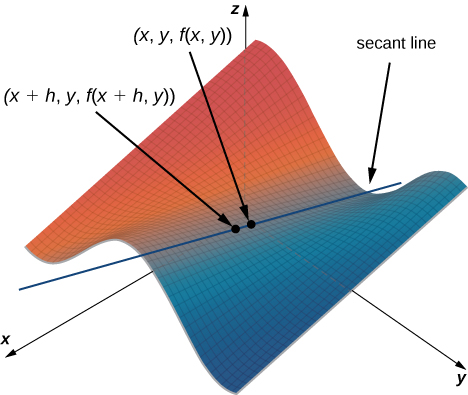
На$\PageIndex{1}$ малюнку значення$h$ позитивне. Якщо$f(x,y)$ графувати і$f(x+h,y)$ для довільної точки,$(x,y),$ то нахил січної лінії, що проходить через ці дві точки, задається

$$\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber$$

Ця лінія паралельна$x$ -осі. Тому нахил січної лінії являє собою середню швидкість зміни функції, коли ми$f$ рухаємося паралельно$x$ -осі. У міру$h$ наближення до нуля нахил січної лінії наближається до нахилу дотичної лінії.

Якщо ми вирішимо змінити$y$ замість$x$ того ж інкрементного значення$h$, то січна лінія паралельна$y$ -осі і так дотична лінія. Тому$∂f/∂x$ являє собою нахил дотичної лінії, що проходить через точку,$(x,y,f(x,y))$ паралельну$x$ -осі, і$∂f/∂y$ являє собою нахил дотичної лінії, що проходить через точку,$(x,y,f(x,y))$ паралельну$y$ -осі. Якщо ми хочемо знайти нахил дотичної лінії, що проходить через ту ж точку в будь-якому іншому напрямку, то нам потрібно те, що називається спрямованими похідними.

Тепер ми повернемося до ідеї контурних карт, яку ми ввели в Функції декількох змінних. Ми можемо використовувати контурну карту для оцінки часткових похідних функції$g(x,y)$.

Приклад$\PageIndex{3}$: Partial Derivatives from a Contour Map

Використовуйте карту контурів$(\sqrt{5},0)$ для оцінки$∂g/∂x$ в точці функції

$$g(x,y)=\sqrt{9−x^2−y^2}. \nonumber$$

Рішення

Рисунок$\PageIndex{2}$ представляє контурну карту для функції$g(x,y)$.

Малюнок$\PageIndex{2}$: Контурна карта для функції$g(x,y)=\sqrt{9−x^2−y^2}$, використовуючи$c=0,1,2,$ та$3 (c=3$ відповідає початковій точці).

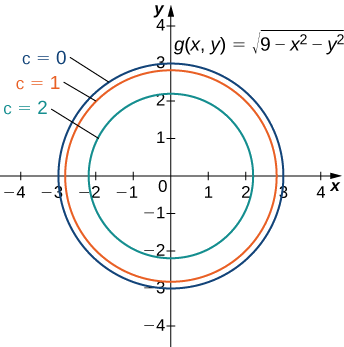
Внутрішнє коло на карті контуру відповідає,$c=2$ а наступне коло відповідає$c=1$. Перше коло задається рівнянням$2=\sqrt{9−x^2−y^2}$; друге коло задається рівнянням$1=\sqrt{9−x^2−y^2}$. Перше рівняння спрощує до,$x^2+y^2=5$ а друге рівняння спрощує до$x^2+y^2=8.$$x$ -перехоплення першого кола є$(\sqrt{5},0)$ і$x$ -перехоплення другого кола є$(2\sqrt{2},0)$. Оцінити величину$∂g/∂x$ оціненого в точці можна$(\sqrt{5},0)$ за формулою нахилу:

$$\begin{align*} \left.\dfrac{∂g}{∂x}\right|_{(x,y) = (\sqrt{5},0)} &≈ \dfrac{g(\sqrt{5},0)−g(2\sqrt{2},0)}{\sqrt{5}−2\sqrt{2}} \\ &= \dfrac{2−1}{\sqrt{5}−2\sqrt{2}} \\ &=\dfrac{1}{\sqrt{5}−2\sqrt{2}} ≈−1.688. \end{align*}$$

Щоб обчислити точне значення$∂g/∂x$ оцінюється в точці$(\sqrt{5},0)$, почнемо з знаходження за$∂g/∂x$ допомогою правила ланцюга. Спочатку перепишемо функцію як

$$g(x,y)=\sqrt{9−x^2−y^2}=(9−x^2−y^2)^{1/2} \nonumber$$

а потім диференціювати по відношенню до,$x$ утримуючи$y$ постійну:

$$\begin{align*} \dfrac{∂g}{∂x} &=\dfrac{1}{2}(9−x^2−y^2)^{−1/2}(−2x) \\[4pt] &=−\dfrac{x}{\sqrt{9−x^2−y^2}}. \end{align*}$$

Далі оцінюємо цей вираз за допомогою$x=\sqrt{5}$ і$y=0$:

\ [\ почати {вирівнювати*}\ dfrac {g} {x} _ {(x, y) = (\ sqrt {5} ,0)} &=−\ dfrac {\ sqrt {5}} {\ sqrt {9− (\ sqrt {5}) ^2− (0) ^2}}\\ [4pt]
&= −\ dfrac {\ sqrt {5}} {\ sqrt {4}}\\ [4pt]
&=−\ drac {\ sqrt {5}} {2} ≈−1.118. \ end {вирівнювати*}\ nonumber\]

Кошторис для часткової похідної відповідає нахилу січної лінії, що проходить через точки$(\sqrt{5},0,g(\sqrt{5},0))$ і$(2\sqrt{2},0,g(2\sqrt{2},0))$. Він являє собою наближення до нахилу дотичної лінії до поверхні через точку$(\sqrt{5},0,g(\sqrt{5},0)),$, яка паралельна$x$ -осі.

Вправа$\PageIndex{3}$

Використовуйте карту контурів для оцінки$∂f/∂y$ в точці$(0,\sqrt{2})$ для функції

$$f(x,y)=x^2−y^2.\nonumber$$

Порівняйте це з точною відповіддю.

Підказка

Створіть контурну карту для$f$ використання значень$c$ від$−3$ до$3$. Яка з цих кривих проходить через точку$(0,\sqrt{2})?$

Відповідь

Використовуючи криві, відповідні$c=−2$ і$c=−3,$ отримуємо

\ [\ begin {вирівнювати*}\ ліворуч. \ dfrac {f} {y}\ право|_ {(x, y) = (0,\ sqrt {2})} &≈\ dfrac {f (0,\ sqrt {3}) −f (0,\ sqrt {2})} {\ sqrt {3}}\\ [4pt]
&=\ dfrac {−−3− (−2)} {\ sqrt {3} −\ sqrt {2}} ⋅\ drac {\ sqrt {3} +\ sqrt {3}} {\ sqrt {3} +\ sqrt {2}}\\ [4pt]
&=−\ sqrt {3} −\ sqrt {2} ≈−3.146. \ end {вирівнювати*}\]

Точна відповідь

$$\left. \dfrac{∂f}{∂y} \right|_{(x,y)=(0,\sqrt{2})}=(−2y|_{(x,y)=(0,\sqrt{2})}=−2\sqrt{2}≈−2.828. \nonumber$$

Функції більше двох змінних

Припустимо, у нас є функція трьох змінних, таких як$w=f(x,y,z).$ Ми можемо обчислити часткові похідні щодо будь-якої$w$ з незалежних змінних, просто як розширення визначень для часткових похідних функцій двох змінних.

Визначення: Часткові похідні

$f(x,y,z)$Дозволяти бути функцією трьох змінних. Потім часткова$f$ похідна по відношенню до$x$, написана як$∂f/∂x,$ або$f_x,$ визначається бути

$$\dfrac{∂f}{∂x}=f_x(x,y,z)=\lim_{h→0}\dfrac{f(x+h,y,z)−f(x,y,z)}{h}. \label{PD2a}$$

Часткова$f$ похідна щодо$y$, написана як$∂f/∂y$$f_y$, або, визначається як

$$\dfrac{∂f}{∂y}=f_y(x,y,z)=\lim_{k→0}\dfrac{f(x,y+k,z)−f(x,y,z)}{k.} \label{PD2b}$$

Часткова$f$ похідна щодо$z$, написана як$∂f/∂z$$f_z$, або, визначається як

$$\dfrac{∂f}{∂z}=f_z(x,y,z)=\lim_{m→0}\dfrac{f(x,y,z+m)−f(x,y,z)}{m}. \label{PD2c}$$

Ми можемо обчислити часткову похідну функції трьох змінних, використовуючи ту саму ідею, яку ми використовували для функції двох змінних. Наприклад, якщо у нас є функція$f$$x,y$, і, і ми хочемо обчислити$z$$∂f/∂x$, то ми ставимося до двох інших незалежних змінних так, ніби вони є константами, а потім диференціювати по відношенню до$x$.

Приклад$\PageIndex{4}$: Calculating Partial Derivatives for a Function of Three Variables

Використовувати граничне визначення частинних похідних$∂f/∂x$ для обчислення функції

$$f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z. \nonumber$$

Потім знайдіть$∂f/∂y$ і$∂f/∂z$ встановивши інші дві змінні постійну і диференціюючи відповідно.

Рішення:

Спочатку ми обчислюємо$∂f/∂x$ за допомогою Equation\ ref {PD2a}, потім обчислимо дві інші часткові похідні, утримуючи інші змінні постійними. Щоб використовувати рівняння для пошуку$∂f/∂x$, нам спочатку потрібно обчислити$f(x+h,y,z):$

\ [\ почати {вирівнювати*} f (x+h, y, z) &= (x+h) ^2−3 (x+h) y+2y^2−4 (x+h) z+5yz ^2−12 (x+h) +4y−3z\\ [4pt]
&= x^2+2xh+h^2−3xy-2y^2−4xz−4гц+5yz^2−12х−12х+4y−3z\ end {align*}\ nonumber\]

і нагадаємо, що$f(x,y,z)=x^2−3xy+2y^2−4zx+5yz^2−12x+4y−3z.$ Далі ми підставляємо ці два вирази в рівняння:

\ [\ почати {вирівнювати*}\ dfrac {f} {x} &=\ lim_ {h→0}\ ліворуч [\ dfrac {x^2+2xh+h^2−3hy−3hy^2y^2y^2y^2y^2y^2−x−2y^2y^2−2y^2y^2−2y^2y^2−2y^2−2y^2y^2−2y^2y^2−2y^2y^2−2y^2y^2−2y^2y^2−24xz+5yz^2−12x+4y−3z} {h}\ праворуч]\\ [4pt]
&=\ lim_ {h→0}\ ліворуч [\ dfrac {2xh+h^2−3hy−4h−12h} {h}\ праворуч]\\\ [4pt]
&=\ lim_ {h → 0}\ ліворуч [\ dfrac {ч (2х+ч−3р−4з−12) )} {h}\ праворуч]\\ [4pt]
&=\ lim_ {h→0} (2x+h−3y−4z−12)\\ [4pt]
&=2x−3y−4z−12. \ end {вирівнювати*}\ nonumber\]

Потім знаходимо$∂f/∂y$ за допомогою утримання$x$ і$z$ постійної. Тому будь-який термін, який не включає змінну,$y$ є постійним, а його похідна дорівнює нулю. Ми можемо застосувати правила суми, різниці та потужності для функцій однієї змінної:

\ [\ почати {вирівнювати*} &\ dfrac {} {y}\ ліворуч [x^2−3xy+2y^2−4x+5yz^2−12x+4y−3z\ праворуч]\\ [4pt]
&=\ dfrac {} {y} [x^2] −\ dfrac {} {y} [x^2] −\ dfrac {y} [3xy] +\ dfrac {} {y} [2y^2] −\ dfrac {y} {y} [4xz] +\ dfrac {y} [5yz^2] −\ dfrac {y} [12x] +\ dfrac {} {y} [4y] −\ dfrac {} z} [3z]\\ [4pt]
&=0−3x+4y−0+5z^2−0+4−0 \\ [4пт]
&=−3х+4й+5з^2+4. \ end {вирівнювати*}\]

Для обчислення$∂f/∂z,$ утримуємо$x$ і$y$ константу і застосовуємо правила суми, різниці та потужності для функцій однієї змінної:

\ [\ почати {вирівнювати*} &\ dfrac {} {z} [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z]\\ [4pt]
&=\ dfrac {z} {z} [x^2] −\ dfrac {} {z} [3xy] +\ dfrac c {} {z} [2y^2] −\ dfrac {z} [4xz] +\ dfrac {z} [5yz^2] −\ dfrac {} {z} [12x] +\ dfrac {} {z} [4y] −\ dfrac {} {z} [3z]\\ [4pt]
&=0−0+0−4x+10yz−0+0−3\\ [4pt]
&=−4x+10yz−3\ кінець {align*}\]

Вправа$\PageIndex{4}$

Використовувати граничне визначення частинних похідних$∂f/∂x$ для обчислення функції

$$f(x,y,z)=2x^2−4x^2y+2y^2+5xz^2−6x+3z−8.\nonumber$$

Потім знайдіть$∂f/∂y$ і$∂f/∂z$ встановивши інші дві змінні постійну і диференціюючи відповідно.

Підказка

Використовуйте стратегію в попередньому прикладі.

Відповідь

$\dfrac{∂f}{∂x}=4x−8xy+5z^2−6,\dfrac{∂f}{∂y}=−4x^2+4y,\dfrac{∂f}{∂z}=10xz+3$

Приклад$\PageIndex{5}$: Calculating Partial Derivatives for a Function of Three Variables

Обчисліть три часткові похідні наступних функцій.

1. $f(x,y,z)=x^2y−4xz+y^2x−3yz$
2. $g(x,y,z)=\sin(x^2y−z)+\cos(x^2−yz)$

Рішення

У кожному випадку розглядайте всі змінні як константи, крім тієї, часткову похідну якої ви обчислюєте.

а.

\ [\ почати {вирівнювати*}\ dfrac {f} {x} &=\ dfrac {} {x}\ ліворуч [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ праворуч]\\ [6pt]
&=\ dfrac {\ dfrac {} {x} (x−3yz} z+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {x} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(2xy−4z) (x−3yz) − (x^2y4x−z+y^2) (1)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {2x^2y−6xy^2z−4xz+12yz^2−x^2y+4xz−y^2} {(x−3yz) ^2}\\ [6пт]
&=\ dfrac {x^2y−6xy^2z−4xz+12yz^2+4xz−y^2} {3yz) ^2}\ кінець {вирівнювати*}\]

\ [\ почати {вирівнювати*}\ dfrac {f} {y} &=\ dfrac {} {y}\ ліворуч [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ праворуч]\\ [6pt]
&=\ dfrac {\ dfrac {} {y} (x−3yz}\ праворуч]\ [6pt] &=\ dfrac {\ dfrac {} {y} (x−3yz} z+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {y} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(x^2+2y) (x−3yz) − (x^2yz) − (x^2y4x−z+y^2) (−3z)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^3x^2yz+2xy−6y^2z+3x^2yz−12xz^2xz^2y^2z} {(x−3yz) ^2}\\ [6пт]
&=\ dfrac {x^3xy−3y^2y^2z^2z^2} {(x−3yz) ^2} {(x−3yz) ^2}\ end {вирівнювати*}\]

\ [\ почати {вирівнювати*}\ dfrac {f} {z} &=\ dfrac {} {z}\ ліворуч [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ праворуч]\\ [6pt]
&=\ dfrac {\ dfrac {} {z} (x−3yz} z+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {z} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(−4x) (x−3yz) − (x^2y−4xz+y ^ 2) (−3y)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {−4x^2+12xyz+3x^2y^2yz+3y^3} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {−4x^2+3x^2y^2y^3} {(x−3yz) ^2}\ кінець {align*}\

б.

\ [\ почати {вирівнювати*}\ dfrac {f} {x} &=\ dfrac {} {x}\ ліворуч [\ sin (x^2y−z) +\ cos (x^2−yz)\ праворуч]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {x} (x^^2y−z) 2y−z) − (\ sin (x^2−yz))\ dfrac {} {x} (x^2−yz)\\ [6pt]
&=2xy\ cos (x^2y−z) −2x\ sin (x^2−yz)\ кінець {вирівнювати*}\]

\ [\ почати {вирівнювати*}\ dfrac {f} {y} &=\ dfrac {} {y} [\ sin (x^2y−z) +\ cos (x^2−yz)]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {y} (xx2^y−z)) − (\ sin (x^2−yz))\ dfrac {} {y} (x^2−yz)\\ [6pt]
&=x^2\ cos (x^2y−z) +z\ sin (x^2−yz)\ end {align*}\]

\ [\ почати {вирівнювати*}\ dfrac {f} {z} &=\ dfrac {} {z} [\ sin (x^2y−z) +\ cos (x^2−yz)]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {z} (xx2^y−z)) − (\ sin (x^2−yz))\ dfrac {} {z} (x^2−yz)\\ [6pt]
&=−\ cos (x^2y−z) +y\ sin (x^2−yz)\ кінець {align*}\ nonumber\]

Вправа$\PageIndex{5}$

Розрахувати$∂f/∂x, ∂f/∂y,$ і$∂f/∂z$ для функції

$$f(x,y,z)=\sec(x^2y)−\tan(x^3yz^2). \nonumber$$

Підказка

Використовуйте стратегію в попередньому прикладі.

Відповідь

$\dfrac{∂f}{∂x}=2xy\sec(x^2y)\tan(x^2y)−3x^2yz^2\sec^2(x^3yz^2)$

$\dfrac{∂f}{∂y}=x^2\sec(x^2y)\tan(x^2y)−x^3z^2\sec^2(x^3yz^2)$

$\dfrac{∂f}{∂z}=−2x^3yz\sec^2(x^3yz^2)$

Часткові похідні вищого порядку

Розглянемо функцію

$$f(x,y)=2x^3−4xy^2+5y^3−6xy+5x−4y+12. \nonumber$$

Його частковими похідними є

$$\dfrac{∂f}{∂x}=6x^2−4y^2−6y+5 \nonumber$$

і

$$\dfrac{∂f}{∂y}=−8xy+15y^2−6x−4. \nonumber$$

Кожна з цих часткових похідних є функцією двох змінних, тому ми можемо обчислити часткові похідні цих функцій. Так само, як і у випадку з похідними однозмінних функцій, ми можемо назвати ці похідні другого порядку, похідні третього порядку і так далі. Взагалі їх називають частковими похідними вищого порядку. Існує чотири часткові похідні другого порядку для будь-якої функції (за умови, що всі вони існують):

\ [\ почати {вирівнювати*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ ліворуч [\ dfrac {f} {x}\ праворуч]\
\ [4pt]\ dfrac {^2f} {yx} &=\ dfrac {} {y}\ лівий\ dfrac {f} {x}\ праворуч]\\ [4pt]
\ dfrac {^2f} {xy} &=\ dfrac {x}\ ліворуч [\ dfrac {f} {y}\ праворуч]\\ [4pt]
\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ лівий [\ dfrac {f} {y}\ праворуч]. \ end {вирівнювати*}\]

Альтернативним позначенням для кожного є$f_{xx},f_{xy},f_{yx},$ і$f_{yy}$, відповідно. Часткові похідні вищого порядку, обчислені відносно різних змінних, таких як$f_{xy}$ і$f_{yx}$, прийнято називати змішаними частинними похідними.

Приклад$\PageIndex{6}$: Calculating Second Partial Derivatives

Обчислити всі чотири секундні часткові похідні для функції

$$f(x,y)=xe^{−3y}+\sin(2x−5y).\label{Ex6e1}$$

Рішення:

Щоб розрахувати$\dfrac{∂^2f}{∂x^2}$ і$\dfrac{∂^2f}{∂y∂x}$, спочатку обчислюємо$∂f/∂x$:

$$\dfrac{∂f}{∂x}=e^{−3y}+2\cos(2x−5y). \label{Ex6e2}$$

Для обчислення$\dfrac{∂^2f}{∂x^2}$ диференціюють$∂f/∂x$ (Equation\ ref {Ex6E2}) щодо$x$:

\ [\ почати {вирівнювати*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ ліворуч [\ dfrac {f} {x} {x} {x} {f} {f} +2\ cos (2x−5y)]\ [6pt]
&=−4\ sin (2x−5y).
\ end {вирівнювати*}\ nonumber\]

Для обчислення$\dfrac{∂^2f}{∂y∂x}$ диференціюють$∂f/∂x$ (Equation\ ref {Ex6E2}) щодо$y$:

\ [\ почати {вирівнювати*}\ dfrac {^2f} {y\, x} &=\ dfrac {} {y}\ ліворуч [\ dfrac {f} {x}\ праворуч]\\ [6pt]
&=\ dfrac {} {y} [e^ {−3y} +2\ cos (2x-5y)\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {вирівнювати*}\ nonumber\]

Щоб розрахувати$\dfrac{∂^2f}{∂x∂y}$ і$\dfrac{∂^2f}{∂y^2}$, спочатку обчислити$∂f/∂y$:

$$\dfrac{∂f}{∂y}=−3xe^{−3y}−5\cos(2x−5y). \label{Ex6e5}$$

Для обчислення$\dfrac{∂^2f}{∂x∂y}$ диференціюють$∂f/∂y$ (Equation\ ref {ex6e5}) щодо$x$:

\ [\ почати {вирівнювати*}\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ ліворуч [\ dfrac {f} {y}\ праворуч]\\ [6pt]
&=\ dfrac {} {x} [−3xe^ {−3y} −5\ cos (2x5−y)]\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {вирівнювати*}\ nonumber\]

Для обчислення$\dfrac{∂^2f}{∂y^2}$ диференціюють$∂f/∂y$ (Equation\ ref {ex6e5}) щодо$y$:

\ [\ почати {вирівнювати*}\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ ліворуч [\ dfrac {f} {y} {y} {y} {f} {f} {−3y} −5\ cos (2x5−y)]\\ [6pt]
&=9xe^ {−3y} −25\ sin (2x−5y).
\ end {вирівнювати*}\ nonumber\]

Вправа$\PageIndex{6}$

Обчислити всі чотири секундні часткові похідні для функції

$$f(x,y)=\sin(3x−2y)+\cos(x+4y).\nonumber$$

Підказка

Виконайте ті ж дії, що і в попередньому прикладі.

Відповідь

$\dfrac{∂^2f}{∂x^2}=−9\sin(3x−2y)−\cos(x+4y)$

$\dfrac{∂^2f}{∂y∂x}=6\sin(3x−2y)−4\cos(x+4y)$

$\dfrac{∂^2f}{∂x∂y}=6\sin(3x−2y)−4\cos(x+4y)$

$\dfrac{∂^2f}{∂y^2}=−4\sin(3x−2y)−16\cos(x+4y)$

На цьому етапі ми повинні помітити, що як у$\PageIndex{6}$ прикладі, так і в контрольно-пропускній пункті це було правда$\dfrac{∂^2f}{∂y∂x}=\dfrac{∂^2f}{∂x∂y}$. При певних умовах це завжди вірно. По суті, це прямий наслідок наступної теореми.

Рівність змішаних частинних похідних (теорема Клеро)

Припустимо,$f(x,y)$ що визначено на відкритому диску$D$, який містить точку$(a,b)$. Якщо функції$f_{xy}$ і$f_{yx}$ безперервні$D$, то$f_{xy}=f_{yx}$.

Теорема Клеро гарантує, що до тих пір, поки змішані похідні другого порядку є неперервними, порядок, в якому ми вибираємо диференціювати функції (тобто яка змінна йде спочатку, потім друга і так далі) не має значення. Він також може бути поширений на похідні вищого порядку. Доказ теореми Клеро можна знайти в найсучасніших книгах з числення.

Дві інші часткові похідні другого порядку можна обчислити для будь-якої функції$f(x,y).$. Часткова похідна$f_{xx}$ дорівнює частковій похідній по відношенню до$x$, і$f_{yy}$ дорівнює частковій похідній по$f_y$ відношенню до$y$.$f_x$

Рівняння з частинними по

Раніше ми вивчали диференціальні рівняння, в яких невідома функція мала одну незалежну змінну. Рівняння з частинними похідними - це рівняння, яке включає в себе невідому функцію більш ніж однієї незалежної змінної і однієї або декількох її частинних похідних. Прикладами рівнянь з частинними похі

$$\underset{\text{heat equation in two dimensions}}{u_t=c^2(u_{xx}+u_{yy})} \nonumber$$

$$\underset{\text{wave equation in two dimensions}}{u_{tt}=c^2(u_{xx}+u_{yy})} \nonumber$$

$$\underset{\text{Laplace’s equation in two dimensions}} {u_{xx}+u_{yy}=0} \nonumber$$

У теплових і хвильових рівняннях невідома функція$u$ має три незалежні змінні:$t$,$x$, а$y$ with$c$ - довільна константа. Незалежні змінні$x$ і$y$ вважаються просторовими змінними, а змінна$t$ представляє час. У рівнянні Лапласа невідома функція$u$ має дві незалежні змінні$x$ і$y$.

Приклад$\PageIndex{7}$: A Solution to the Wave Equation

Переконайтеся, що

$$u(x,y,t)=5\sin(3πx)\sin(4πy)\cos(10πt) \nonumber$$

це рішення хвильового рівняння

$$u_{tt}=4(u_{xx}+u_{yy}). \label{Ex7Eq2}$$

Рішення

Спочатку розраховуємо$u_{tt},u_{xx},$ і$u_{yy}:$

\ [\ почати {вирівнювати*} u_ {tt} (x, y, t) &=\ dfrac {} {t}\ ліворуч [\ dfrac {u} {t} {t} {t} {t} {t}\ sin (3πx)\ sin (4πy) (−10π\ sin) (−10π\ sin πt))]\\ [6pt]
&=\ dfrac {} {t}\ ліворуч [−50π\ sin (3πx)\ sin (4πy)\ sin (10πt)\ право]\\ [6пт]
&= −500π^2\ sin (3πx)\ грін (4πy)\ cos (10πt)\
кінець {вирівнювати*}\]

\ [\ почати {вирівнювати*} u_ {xx} (x, y, t) &=\ dfrac {} {x}\ ліворуч [\ dfrac {u} {x}\ праворуч]\\ [6pt]
&=\ dfrac {} {x}\ ліворуч [15π\ cos (3πx)\ sin (4πy)\ cos (4πy)\ cos (4πy)\ cos (10πy) t)\ праворуч]\\ [6pt]
&=−45π^2\ sin (3πx)\ sin (4πy)\ cos (10πt)\ кінець {align*}\]

\ [\ почати {вирівнювати*} u_ {yy} (x, y, t) &=\ dfrac {} {y}\ лівий [\ dfrac {u} {y} {u} {u} {y} {y}\ лівий [5\ sin (3πx) (4π\ cos (4πy)\ cos (4πy)\ cos (4πy) (10πt)\ праворуч]\\ [6пт]
&=\ dfrac {} {y}\ ліворуч [20π\ sin (3πx)\ cos (4πy)\ cos (10πt)\ право]\\ [6пт]
&= −80π^2\ sin (3πx)\ sin (4πy)\ cos (
10πт). \ end {вирівнювати*}\ nonumber\]

Далі ми підставляємо кожну з них в праву частину Equation\ ref {Ex7Eq2} і спрощуємо:

\ [\ почати {вирівнювати*} 4 (u_ {xx} +u_ {yy}) &= 4 (−45π^2\ sin (3πx)\ sin (4πy)\ cos (10πt) +−80π^2\ sin (3πx)\ sin (4πy)\ cos (10πt))\ [6пт]
&= 4 (125π-y)\ cos (10πt))\ [6pt] &4 (125π^^ 2\ sin (3πx)\ sin (4πy)\ cos (10πt))\\ [6пт]
&=−500π^2\ sin (3πx)\ sin (4πy)\ cos (10πt)\\ [6pt]
&=u_ {tt}. \ end {вирівнювати*}\]

Це перевіряє рішення.

Вправа$\PageIndex{7}$: A Solution to the Heat Equation

Переконайтеся, що

$$u(x,y,t)=2\sin \left(\dfrac{x}{3} \right)\sin\left(\dfrac{y}{4} \right)e^{−25t/16} \nonumber$$

це рішення рівняння тепловіддачі

$$u_t=9(u_{xx}+u_{yy}). \nonumber$$

Підказка

Обчисліть часткові похідні і підставити в праву частину.

Відповідь

ТАБ

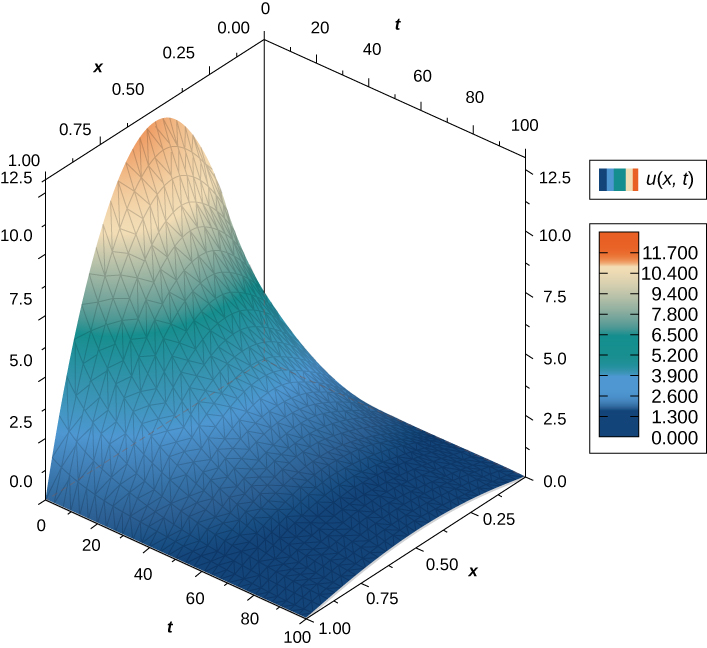
Оскільки розв'язання двовимірного рівняння теплопровідності є функцією трьох змінних, створити візуальне уявлення рішення непросто. Ми можемо графікувати рішення для фіксованих значень$t,$, які складають знімки розподілів тепла у фіксований час. Ці знімки показують, як тепло розподіляється по двовимірній поверхні з плином часу. Графік попереднього рішення за часом$t=0$ відображається на рисунку$\PageIndex{3}$. З часом крайнощі вирівнюються, наближаючись до нуля, коли наближається до нескінченності.$t$

Малюнок$\PageIndex{3}$

Якщо розглядати рівняння теплоємності в одному вимірі, то можна проводити графік рішення з плином часу. Рівняння теплоти в одному вимірі стає

$$u_t=c^2u_{xx}, \nonumber$$

де$c^2$ являє собою теплову дифузійність розглянутого матеріалу. Розв'язок цього диференціального рівняння можна записати у вигляді

$$u_m(x,t)=e^{−π^2m^2c^2t}\sin(mπx) \nonumber$$

де$m$ - будь-яке натуральне число. Графік використання цього рішення$m=1$ відображається на малюнку$\PageIndex{4}$, де початковий розподіл температури по дроту довжини$1$ задається$u(x,0)=\sin πx.$ Зауваження, що з плином часу провід охолоджується. Це видно тому, що зліва направо найвища температура (яка виникає посередині дроту) знижується і змінює колір з червоного на синій.

Рисунок$\PageIndex{4}$: Графік розв'язку рівняння теплоємності в одному вимірі за часом.

Лорд Кельвін і епоха Землі

Протягом кінця 1800-х років вчені нової галузі геології прийшли до висновку, що Землі має бути «мільйони і мільйони» років. Приблизно в цей же час Чарльз Дарвін опублікував свій трактат про еволюцію. Думка Дарвіна полягала в тому, що еволюції потрібно багато мільйонів років, і він висловив сміливе твердження, що крейдяні поля Weald, де були знайдені важливі скам'янілості, були наслідком$300$ мільйонної ерозії.

Малюнок$\PageIndex{5}$: (а) Вільям Томсон (лорд Кельвін), 1824-1907 рр., був британським фізиком та інженером-електриком; (б) Кельвін використовував рівняння дифузії тепла для оцінки віку Землі (кредит: модифікація роботи НАСА).

У той час видатний фізик Вільям Томсон (лорд Кельвін) використовував важливе рівняння з частинними похідними, відоме як рівняння дифузії тепла, щоб оцінити вік Землі, визначивши, скільки часу знадобиться Землі, щоб охолонути від розплавленої породи до того, що ми мали в той час. Його висновок становив діапазон від 20 до 400 мільйонів років, але, швидше за все, близько 50 мільйонів років. Протягом багатьох десятиліть проголошення цієї незаперечної ікони науки погано сиділи ні у геологів, ні з Дарвіном.

• Прочитайте статтю Кельвіна про оцінку віку Землі.

Кельвін зробив розумні припущення, грунтуючись на тому, що було відомо свого часу, але він також зробив кілька припущень, які виявилися неправильними. Одне невірне припущення полягало в тому, що Земля тверда і що охолодження, отже, відбувалося лише через провідність, отже, виправдовуючи використання рівняння дифузії. Але найсерйознішою помилкою було прощення - упущення того факту, що Земля містить радіоактивні елементи, які постійно постачають тепло під мантією Землі. Відкриття радіоактивності наблизилося до кінця життя Кельвіна, і він визнав, що його розрахунок доведеться змінити.

Кельвін використовував просту одновимірну модель, застосовану лише до зовнішньої оболонки Землі, і вивів вік з графіків та приблизно відомого градієнта температури поблизу поверхні Землі. Давайте розглянемо більш підходящий варіант рівняння дифузії в радіальних координатах, який має вигляд

$$\dfrac{∂T}{∂t}=K\left[\dfrac{∂^2T}{∂^2r}+\dfrac{2}{r}\dfrac{∂T}{∂r}\right] \label{kelvin1}$$ .

Тут температура як функція$r$ (вимірюється від центру Землі), а час$t. K$ - теплопровідність - для розплавленої гірської породи, в даному випадку.$T(r,t)$ Стандартним методом розв'язання такого рівняння з частинними похідними є поділ змінних, де ми виражаємо рішення як добуток функцій, що містять кожну змінну окремо. У цьому випадку ми б записували температуру як

$$T(r,t)=R(r)f(t). \nonumber$$

1. Підставляємо цю форму в Equation\ ref {kelvin1} і, зазначивши, що$f(t)$ є постійною по відношенню до відстані$(r)$ і$R(r)$ є постійною по відношенню до часу$(t)$, показати, що $$\dfrac{1}{f}\dfrac{∂f}{∂t}=\dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]. \nonumber$$
2. Це рівняння представляє поділ змінних, які ми хочемо. Ліва сторона є лише функцією,$t$ а права сторона є лише функцією$r$, і вони повинні бути рівними для всіх значень$r$ і$t$. Тому вони обидва повинні дорівнювати константі. Давайте назвемо це постійним$−λ^2$. (Зручність такого вибору видно на заміні.) Отже, у нас є $$\dfrac{1}{f}\dfrac{∂f}{∂t}=−λ^2 \text{and} \dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]=−λ^2. \nonumber$$
3. Тепер ми можемо перевірити шляхом прямої підміни для кожного рівняння, що розв'язки$f(t)=Ae^{−λ^2t}$ і$R(r)=B\left(\dfrac{\sin αr}{r}\right)+C\left(\dfrac{\cos αr}{r}\right)$, де$α=λ/\sqrt{K}$. Зверніть увагу, що$f(t)=Ae^{+λn^2t}$ це також дійсне рішення, тому ми могли б вибрати$+λ^2$ для нашої постійної. Чи можете ви зрозуміти, чому це не буде дійсним для цього випадку зі збільшенням часу?
4. Давайте тепер застосуємо граничні умови.
   1. Температура повинна бути кінцевою в центрі Землі,$r=0$. Яка з двох констант,$B$ або, отже$C$, повинна бути нульовою, щоб тримати$R$ кінцевий на$r=0$? (Нагадаємо, що$\sin(αr)/r→α=$ як$r→0$, але$\cos(αr)/r$ поводиться зовсім по-іншому.)
   2. Кельвін стверджував, що коли магма досягає поверхні Землі, вона дуже швидко остигає. Людина може часто торкатися поверхні протягом тижнів течії. Тому поверхня досягла помірної температури дуже рано і залишалася майже постійною при температурі поверхні$T_s$. Для простоти поставимо$T=0$ на$r=R_E$ і знайдемо α таке, що це температура там за весь час$t$. (Кельвін прийняв значення, щоб бути$300K≈80°F$. Ми можемо додати цю$300K$ константу до нашого рішення пізніше.) Щоб це було true, аргумент синуса повинен дорівнювати нулю$r=R_E$. Зверніть увагу, що α має нескінченний ряд значень, які задовольняють цій умові. Кожне значення$α$ представляє дійсне рішення (кожне зі своїм значенням для$A$). Загальне або загальне рішення - це сума всіх цих рішень.
   3. При цьому$t=0,$ ми припускаємо, що вся Земля була при початковій гарячій температурі$T_0$ (Кельвін взяв це приблизно$7000K$.) Застосування цієї граничної умови передбачає більш досконале застосування коефіцієнтів Фур'є. Як зазначається в частині b. Кожне значення$α_n$ являє собою дійсне рішення, а загальне рішення є сумою всіх цих розв'язків. Це призводить до послідовного рішення: $$T(r,t)=\left(\dfrac{T_0R_E}{π}\right)\sum_n\dfrac{(−1)^{n−1}}{n}e^{−λn^2t}\dfrac{\sin(α_nr)}{r} \nonumber$$ де$\; α_n=nπ/R_E$.

Зверніть увагу на те, як значення$α_n$ походять від граничної умови, застосованої в частині b. термін$\dfrac{−1^{n−1}}{n}$ є константою$A_n$ для кожного члена ряду, визначеного з застосування методу Фур'є. Дозволивши$β=\dfrac{π}{R_E}$, вивчити перші кілька термінів цього рішення, показаного тут, і зауважте, як$λ^2$ в експоненціальній призводить до того, що вищі терміни швидко зменшуються з плином часу:

$$T(r,t)=\dfrac{T_0R_E}{πr}\left(e^{−Kβ^2t}(\sinβr)−\dfrac{1}{2}e^{−4Kβ^2t}(\sin2βr)+\dfrac{1}{3}e^{−9Kβ^2t}(\sin3βr)−\dfrac{1}{4}e^{−16Kβ^2t}(\sin4βr)+\dfrac{1}{5}e^{−25Kβ^2t}(\sin5βr)...\right). \nonumber$$

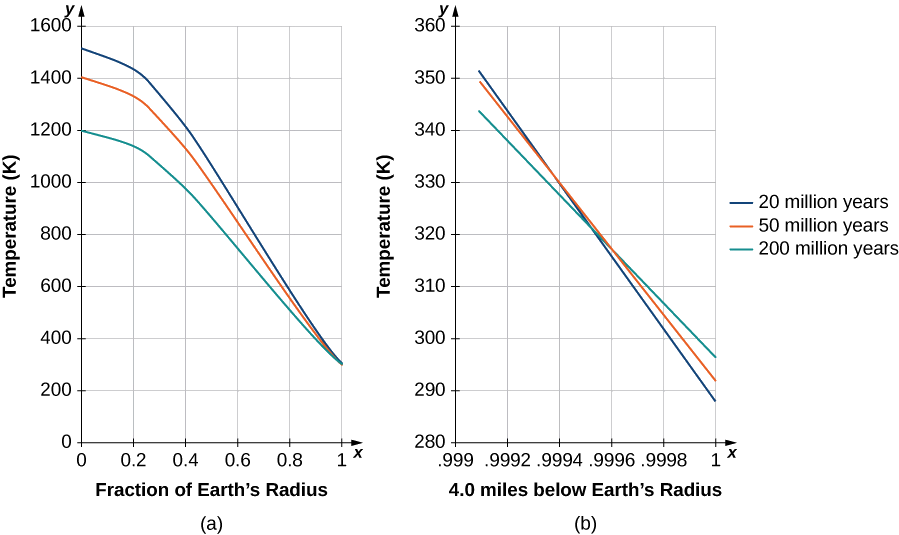
Найближчий час для точності потрібні$t=0,$ багато термінів розв'язання. Вставляючи значення для провідності$K$ і$β=π/R_E$ для часу, що наближається лише тисячі років, лише перші кілька термінів вносять значний внесок. Кельвіну потрібно було лише подивитися на розчин поблизу поверхні Землі (рис.$\PageIndex{6}$) і через довгий час визначити, який час найкраще дав оцінений температурний градієнт, відомий за його епоху ($1°F$збільшення на$50ft$). Він просто вибрав діапазон разів з градієнтом, близьким до цього значення. На малюнку$\PageIndex{6}$ розчини наносяться і масштабуються, з доданою температурою$300−K$ поверхні. Зверніть увагу, що центр Землі був би відносно прохолодним. У той час вважалося, що Земля повинна бути твердою.

Малюнок$\PageIndex{6}$: Температура проти радіальної відстані від центру Землі. (a) Результати Кельвіна, побудовані в масштабі. (b) Крупний план результатів на глибині$4.0$ миль нижче поверхні Землі.

Епілог

20 травня 1904 року фізик Ернест Резерфорд виступив у Королівському інституті, щоб оголосити переглянутий розрахунок, який включав внесок радіоактивності як джерела тепла Землі. За власними словами Резерфорда:

«Я зайшов у кімнату, яка була напівтемною, і тепер помітив лорда Кельвіна в аудиторії, і зрозумів, що мене чекають неприємності в останній частині моєї промови, присвяченій віку Землі, де мої погляди суперечили його. До мого полегшення Кельвін міцно заснув, але коли я підійшов до важливого моменту, я побачив, як стара птиця сідає, відкрила око і півня вусано поглянула на мене.

Потім прийшло раптове натхнення, і я сказав, що Господь Кельвін обмежив вік Землі, за умови, що не було виявлено нового джерела [тепла]. Це пророче висловлювання посилалося на те, що ми зараз розглядаємо сьогодні ввечері, радій! Ось! Старий хлопчик сяяв на мене».

Резерфорд розрахував вік для Землі близько 500 мільйонів років. Сьогодні прийняте значення віку Землі становить близько 4,6 мільярда років.

Ключові концепції

• Часткова похідна - це похідна, що включає функцію більш ніж однієї незалежної змінної.
• Щоб обчислити часткову похідну щодо заданої змінної, розглядайте всі інші змінні як константи і використовуйте звичайні правила диференціації.
• Часткові похідні вищого порядку можуть обчислюватися так само, як і похідні вищого порядку.

Ключові рівняння

Часткова похідна$f$ по відношенню до$x$ $$\dfrac{∂f}{∂x}=\displaystyle{\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h}} \nonumber$$

Часткова похідна$f$ по відношенню до$y$ $$\dfrac{∂f}{∂y}=\displaystyle{\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}} \nonumber$$

Глосарій

часткові похідні вищого порядку

часткові похідні другого порядку або вище, незалежно від того, чи є вони змішаними частковими похідними

змішані часткові похідні

часткові похідні другого порядку або вище, у яких щонайменше дві диференціації мають відношення до різних змінних

часткова похідна

похідна функції більш ніж однієї незалежної змінної, в якій всі змінні, крім однієї, утримуються постійними

рівняння в частинних по

рівняння, яке включає в себе невідому функцію більше, ніж одна незалежна змінна і один або кілька його часткових похідних