2.12: Неявна диференціація та пов'язані з ними ставки

неявна диференціація

У нашій роботі до цих пір функції, які нам потрібно було диференціювати, були або вказані явно\( y=x^2+e^x \), наприклад, або можна було отримати явну формулу для них, наприклад, рішення,\( y^3-3x^2=5 \) щоб отримати\( y=\sqrt[3]{5+3x^2} \). Іноді, однак, у нас буде\(x\) рівняння\(y\), яке або важко, або неможливо вирішити явно\(y\), наприклад\( y+e^y=x^2 \). У будь-якому випадку, ми все ще можемо знайти,\(y' = f'(x)\) використовуючи неявну диференціацію.

Ключова ідея неявної диференціації полягає в тому, щоб припустити, що\(y\) це функція,\(x\) навіть якщо ми не можемо явно вирішити для\(y\). Це припущення не вимагає жодної роботи, але нам потрібно бути дуже обережним, щоб ставитися\(y\) як до функції, коли ми диференціюємо та використовуємо правило ланцюга.

Приклад\(\PageIndex{1}\)

Припустимо, що\(y\) є функцією\(x\). Розрахувати

1. \( \frac{d}{dx}\left( y^3 \right) \)
2. \( \frac{d}{dx}\left( x^3y^2 \right) \)
3. \( \frac{d}{dx}\left( \ln(y) \right) \)

Рішення

1. Нам потрібно правило ланцюга, оскільки y є функцією x:\[ \frac{d}{dx}\left( y^3 \right)=3y^2\frac{dy}{dx}\overset{\text{or}}{=}3y^2y' \nonumber \]
2. Нам потрібно скористатися правилом продукту і Правилом ланцюга:\[ \begin{align*} \frac{d}{dx}\left( x^3y^2 \right) & = x^3\frac{d}{dx}\left( y^2 \right)+y^2\frac{d}{dx}\left( x^3\right) \\ & = x^32y\frac{dy}{dx}+y^23x^2 \\ \overset{\text{or}}{=}& 2x^3yy'+3y^2x^2 \end{align*} \nonumber \]
3. Ми знаємо\( \frac{d}{dx}\left( \ln(x) \right) =\frac{1}{x} \), тому ми використовуємо це і правило ланцюга:\[ \frac{d}{dx}\left( \ln(y) \right)=\frac{1}{y}\cdot y' \nonumber \]

неявна диференціація

Визначити\(y'\), differentiate each side of the defining equation, treating \(y\) as a function of \(x\), and then algebraically solve for \(y'\).

(Останній приклад у наступному відео стає досить брудним - не хвилюйтеся занадто сильно, якщо ви не можете слідувати всім спрощенням в кінці.)

Приклад\(\PageIndex{2}\)

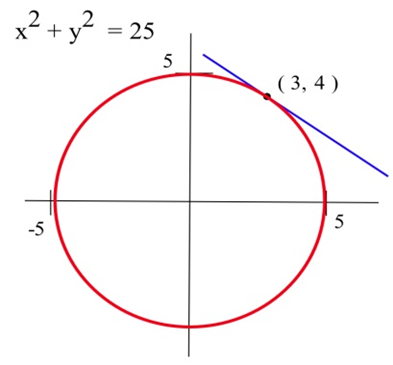
Знайдіть нахил дотичної лінії до кола\(x^2 + y^2 = 25\) в точці (3,4) за допомогою неявної диференціації.

Рішення

Ми диференціюємо кожну сторону рівняння,\(x^2 + y^2 = 25\) а потім вирішуємо для\(y'\):\[ \begin{align*} \frac{d}{dx}\left(x^2+y^2\right) & = \frac{d}{dx}(25)\\ 2x+2yy' & = 0 \end{align*} \nonumber \]

Вирішуючи для\(y'\), ми маємо\( y'=-\frac{2x}{2y}=-\frac{x}{y} \), і, в точці (3,4),\[y'=-\frac{3}{4}.\nonumber \]

У попередньому прикладі було б легко явно вирішити для\(y\), і тоді ми могли б диференціювати,\(y\) щоб отримати\(y'\). Тому що ми могли б явно вирішити для\(y\), у нас був вибір методів для обчислення\(y'\). Іноді, однак, ми не можемо явно вирішити для\(y\), і єдиним способом визначення\(y'\) є використання неявної диференціації.

Пов'язані тарифи

Якщо кілька змінних або величин пов'язані один з одним і деякі змінні змінюються з відомою швидкістю, то ми можемо використовувати похідні, щоб визначити, наскільки швидко інші змінні повинні змінюватися.

Ось посилання на приклади, використані у відео в цьому розділі: Пов'язані тарифи.

Приклад\(\PageIndex{3}\)

Припустимо, межа міста приблизно кругла, і радіус цього кола збільшується зі швидкістю 0,1 миль щороку. Дізнайтеся, як швидко площа міста збільшується, коли радіус становить 5 миль.

Рішення

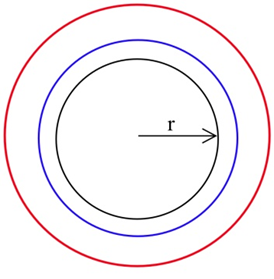
Ми могли б отримати приблизну відповідь, обчисливши площу кола, коли радіус становить 5 миль (\( A = \pi r^2 = \pi (5 \text{ miles})^2 \approx 78.6 \text{ miles}^2 \)) і 1 рік потому, коли радіус на 0,1 фута більше, ніж раніше (\(A = \pi r^2 = \pi (5.1 \text{ miles})^2 \approx 81.7 \text{ miles}^2\)), а потім знаходячи\[ \frac{\Delta \text{Area}}{\Delta \text{time}}=\frac{81.7 \text{ mi}^2 - 78.6 \text{ mi}^2}{1 \text{ year}} = 3.1 \text{ mi}^2/\text{yr}.\nonumber \] Ця приблизна відповідь являє собою середнє зміна площі протягом 1-річного періоду, коли радіус збільшився з 5 миль до 5,1 миль, і відповідав би січному нахилу на графіку площі.

Однак, щоб знайти точну відповідь, нам потрібні похідні. У цьому випадку і радіус, і площа є функціями часу:\[r(t)=\text{ radius at time } t \qquad A(t)=\text{ area at time } t\nonumber \]

Ми знаємо, як швидко змінюється радіус, що є твердженням про похідну:\( \frac{dr}{dt}=0.1\frac{\text{mile}}{\text{year}} \). Ми також знаємо, що\(r = 5\) в наш момент інтерес.

Ми шукаємо, наскільки швидко збільшується площа, що є\( \frac{dA}{dt} \).

Тепер нам потрібно рівняння, що стосується наших змінних, яке є рівнянням площі:\[A=\pi r^2.\nonumber \]

Беручи похідну обох сторін цього рівняння щодо\(t\), можна використовувати неявну диференціацію:\[ \begin{align*} \frac{d}{dt}\left( A \right) & = \frac{d}{dt}\left( \pi r^2 \right)\\ \frac{dA}{dt} & = \pi 2r\frac{dr}{dt} \end{align*} \nonumber \]

Підключення значень, які ми знаємо для\(r\) і\(\frac{dr}{dt}\),\[ \frac{dA}{dt}=\pi 2(5\text{ miles})\left(0.1\frac{\text{miles}}{\text{year}}\right)=\pi\frac{\text{miles}^2}{\text{year}}\nonumber \]

Таким чином, площа міста збільшується приблизно на 3.14 квадратних миль на рік, коли радіус 5 миль.

Пов'язані тарифи

При роботі з пов'язаною проблемою ставок,

1. Намалюйте малюнок (якщо є можливість).
2. Визначте величини, які змінюються, і призначте їм змінні.
3. Знайдіть рівняння, яке пов'язує ці величини.
4. Диференціюйте обидві сторони цього рівняння щодо часу.
5. Підключіть будь-які відомі значення для змінних або швидкості зміни.
6. Вирішуйте за потрібною ставкою.

Приклад\(\PageIndex{4}\)

Компанія визначила криву попиту на свій товар\( q=\sqrt{5000-p^2} \),\(p\) де ціна в доларах,\(q\) а кількість у мільйоні. Якщо погодні умови призводять до зростання ціни на 2 долари на тиждень, знайдіть швидкість, з якою попит змінюється, коли ціна становить 40 доларів.

Рішення

Кількість змінюється є\(p\) і\(q\), і ми припускаємо, що вони обидві функції часу\(t\), у тижнях. У нас вже є рівняння, що стосується величин, тому ми можемо неявно диференціювати його. \[ \begin{align*} \frac{d}{dt}(q) & = \frac{d}{dt}\left(5000-p^2\right)^{1/2} \\ \frac{dq}{dt} & = \frac{1}{2}\left(5000-p^2\right)^{-1/2}\frac{d}{dt}\left(5000-p^2\right) \\ \frac{dq}{dt} & = \frac{1}{2}\left(5000-p^2\right)^{-1/2}\left(-2p\frac{dp}{dt}\right) \end{align*} \nonumber \]

Використовуючи дану інформацію, ми знаємо, що ціна зростає на 2 долари на тиждень, коли ціна становить 40 доларів, даючи\( \frac{dp}{dt}=2 \) коли\(p = 40\). Підключивши ці значення,\[ \frac{dq}{dt} = \frac{1}{2}\left(5000-40^2\right)^{-1/2}\left(-2(40)(2)\right) \approx -1.37 \nonumber \]

Попит падає на 1,37 мільйона позицій на тиждень.

Приклад\(\PageIndex{5}\)

Загальна добова вартість виготовлення\(x\) виробів в день становить\(TC(x) = 300,000 + 4x + \frac{200,000}{x}\). Якщо виробництво нарощувалося на 20 одиниць на день, знайдіть швидкість, з якою загальна щоденна вартість збільшується, якщо вони в даний час виробляють 2000 найменувань.

Рішення

Кількість змінюється є\(x\) і\(TC\), і ми припускаємо, що вони обидві функції часу\(t\), у днях. У нас вже є рівняння, що стосується величин, тому ми можемо неявно диференціювати його. \[ \begin{align*} \frac{d}{dt}(TC) & = \frac{d}{dt}\left(300,000 + 4x + 200,000x^{-1}\right) \\ \frac{d TC}{dt} & = 4\frac{dx}{dt} - 200,000x^{-2}\frac{dx}{dt}\\ \frac{d TC}{dt} & = \left(4 - \frac{200,000}{x^2}\right)\frac{dx}{dt}\\ \end{align*} \nonumber \]

Ми знаємо, що кількість вироблених збільшується на 20 одиниць на тиждень, коли виробництво становить 2000 одиниць, даючи\( \frac{dx}{dt}=20 \) коли\(x = 2000\). Підключивши ці значення,\[ \frac{d TC}{dt} = \left(4 - \frac{200,000}{2000^2}\right)(20) = 79 \nonumber \]

Загальна щоденна вартість збільшується на 79 доларів щодня.