1.2: Основні класи функцій
- Page ID
- 62324
- Обчисліть нахил лінійної функції і інтерпретувати її значення.
- Розпізнати ступінь многочлена.
- Знайдіть коріння квадратичного многочлена.
- Опишіть графіки основних непарних і парних поліноміальних функцій.
- Визначте раціональну функцію.
- Опишіть графіки силових і кореневих функцій.
- Поясніть різницю між алгебраїчними та трансцендентними функціями.
- Графік - кусково визначена функція.
- Намалюйте графік функції, яка була зрушена, розтягнута або відбита від початкового положення графіка.
Ми вивчили загальні характеристики функцій, тому тепер давайте розглянемо деякі конкретні класи функцій. Почнемо з розгляду основних властивостей лінійних і квадратичних функцій, а потім узагальнюємо, щоб включити поліноми вищого ступеня. Поєднуючи кореневі функції з поліномами, ми можемо визначити загальні алгебраїчні функції та відрізнити їх від трансцендентних функцій, які ми розглянемо далі в цій главі. Закінчуємо розділ прикладами кусково визначених функцій і розглянемо, як намалювати графік функції, яка була зрушена, розтягнута або відбита від початкової форми.
Лінійні функції та нахил
Найпростіший тип функції для розгляду - це лінійна функція. Лінійні функції мають вигляд\(f(x)=ax+b\), де\(a\) і\(b\) є константами. На малюнку\(\PageIndex{1}\) ми бачимо приклади лінійних функцій, коли a є додатним, негативним і нулем. Зверніть увагу\(a>0\), що якщо, графік лінії піднімається зі\(x\) збільшенням. Іншими словами,\(f(x)=ax+b\) збільшується на\((−∞, ∞)\). Якщо\(a<0\), графік лінії падає у міру\(x\) збільшення. У цьому випадку\(f(x)=ax+b\) зменшується на\((−∞, ∞)\). Якщо\(a=0\), лінія горизонтальна.
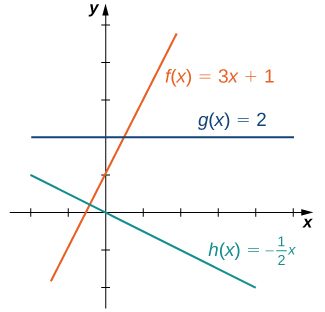
Як пропонує Рисунок\(\PageIndex{1}\), графік будь-якої лінійної функції є лінією. Однією з відмінних рис лінії є її нахил. Нахил - це зміна\(y\) для кожної одиниці зміни в\(x\). Ухил вимірює як крутизну, так і напрямок лінії. Якщо нахил позитивний, лінія вказує вгору при русі зліва направо. Якщо нахил негативний, лінія вказує вниз при русі зліва направо. Якщо ухил дорівнює нулю, лінія горизонтальна. Щоб розрахувати нахил лінії, нам потрібно визначити співвідношення зміни в\(y\) порівнянні зі зміною\(x\). Для цього вибираємо будь-які дві точки\((x_1,y_1)\) і\((x_2,y_2)\) на лінії і обчислюємо\(\dfrac{y_2−y_1}{x_2−x_1}\). На малюнку ми бачимо\(\PageIndex{2}\), що це співвідношення не залежить від обраних пунктів.
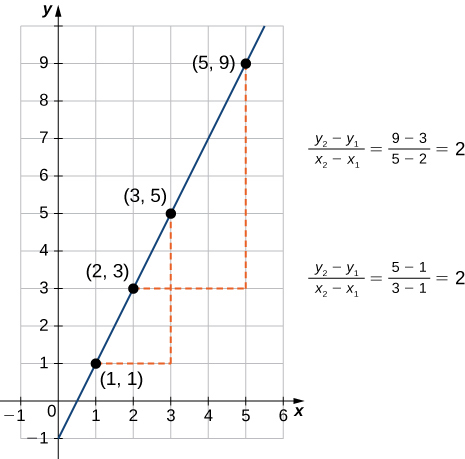
Розглянемо лінію,\(L\) що проходить через точки\((x_1,y_1)\) і\((x_2,y_2)\). Нехай\(Δy=y_2−y_1\) і\(Δx=x_2−x_1\) позначають зміни в\(y\) і\(x\), відповідно. Ухил лінії дорівнює
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx} \nonumber \]
Тепер ми розглянемо зв'язок між нахилом і формулою для лінійної функції. Розглянемо лінійну функцію, задану формулою\(f(x)=ax+b\). Як обговорювалося раніше, ми знаємо, що графік лінійної функції задається рядком. Ми можемо використовувати наше визначення ухилу для обчислення нахилу цієї лінії. Як показано, ми можемо визначити ухил, розрахувавши\((y_2−y_1)/(x_2−x_1)\) для будь-яких точок\((x_1,y_1)\) і\((x_2,y_2)\) на лінії. Оцінюючи функцію\(f\) в\(x=0\), ми бачимо, що\((0,b)\) це точка на цій лінії. Оцінюючи цю функцію на\(x=1\), ми бачимо, що також\((1,a+b)\) є точкою на цій лінії. Тому нахил цієї лінії дорівнює
\[\dfrac{(a+b)−b}{1−0}=a. \nonumber \]
Ми показали, що коефіцієнт\(a\) - це ухил лінії. Можна зробити висновок, що формула\(f(x)=ax+b\) описує лінію з нахилом\(a\). Крім того, оскільки ця лінія перетинає\(y\) -вісь у точці\((0,b)\), ми бачимо, що\(y\) -intercept для цієї лінійної функції є\((0,b)\). Робимо висновок, що формула\(f(x)=ax+b\) говорить нам нахил\(a\), і\(y\) -перехоплення\((0,b)\), для цієї лінії. Оскільки ми часто використовуємо символ\(m\) для позначення нахилу лінії, ми можемо написати
\[\underbrace{f(x)=mx+b}_{\text{slope-intercept form}} \nonumber \]
для позначення нахилу-перехоплення форми лінійної функції.
Іноді буває зручно виражати лінійну функцію по-різному. Наприклад, припустимо, що графік лінійної функції проходить через точку\((x_1,y_1)\) і нахил прямої дорівнює\(m\). Так як будь-яка інша точка\((x,f(x))\) на графіку\(f\) повинна задовольняти рівнянню
\[m=\dfrac{f(x)−y_1}{x−x_1}, \nonumber \]
ця лінійна функція може бути виражена записом
\[\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}. \nonumber \]
Ми називаємо це рівняння рівнянням точкового нахилу для цієї лінійної функції.
Оскільки кожна невертикальна лінія є графіком лінійної функції, точки на невертикальній лінії можна описати за допомогою рівнянь ухил-перехоплення або точка-нахил. Однак вертикальна лінія не представляє графіка функції і не може бути виражена жодною з цих форм. Натомість вертикальна лінія описується рівнянням\(x=k\) для деякої константи\(k\). Оскільки ні форма ухил-перехоплення, ні форма точка-нахил не допускають вертикальних ліній, використовуємо позначення
\[\underbrace{ax+by=c}_{\text{standard form}}, \nonumber \]
де\(a,b\) обидва не нуль, для позначення стандартної форми лінії.
Розглянемо лінію, що проходить через точку\((x_1,y_1)\) з ухилом\(m\). рівняння
\[y−y_1=m(x−x_1) \nonumber \]
рівняння точки-нахилу для цієї лінії.
Розглянемо лінію з нахилом\(m\) і\(y\)\((0,b).\) -перехопленням Рівняння
\[y=mx+b \nonumber \]
це рівняння для цієї лінії у формі перехоплення нахилу.
Стандартна форма прямої задається рівнянням
\[ax+by=c, \nonumber \]
де\(a\) і\(b\) обидва не нуль. Ця форма є більш загальною, оскільки дозволяє проводити вертикальну лінію,\(x=k\).
Розглянемо лінію, що проходить через точки\((11,−4)\) і\((−4,5)\), як показано на малюнку\(\PageIndex{3}\).
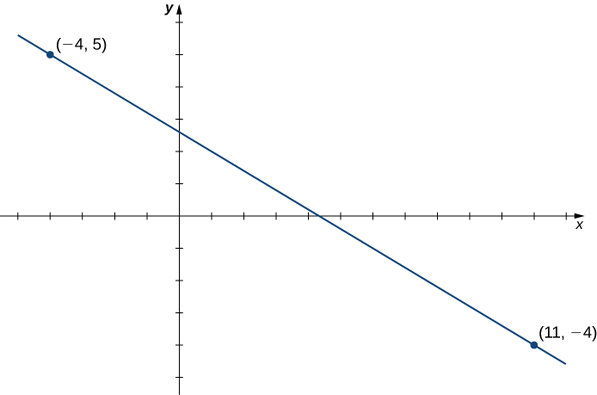
- Знайдіть нахил лінії.
- Знайдіть рівняння для цієї лінійної функції у вигляді точкового нахилу.
- Знайдіть рівняння для цієї лінійної функції у формі нахилу-перехоплення.
Рішення
1. Ухил лінії дорівнює
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber \]
2. Щоб знайти рівняння для лінійної функції у формі точка-нахил, використовуйте нахил\(m=−3/5\) і виберіть будь-яку точку на прямій. Якщо ми виберемо точку\((11,−4)\), то отримаємо рівняння
\[f(x)+4=−\dfrac{3}{5}(x−11). \nonumber \]
3. Щоб знайти рівняння для лінійної функції у формі нахилу-перехоплення, розв'яжіть рівняння в частині b\(f(x)\). for. Коли ми це зробимо, ми отримуємо рівняння
\[f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber \]
Розглянемо лінію, що проходить через точки\((−3,2)\) і\((1,4)\).
- Знайдіть нахил лінії.
- Знайдіть рівняння цієї лінії у формі точки-нахилу.
- Знайдіть рівняння цієї прямої у формі перехоплення нахилу.
- Підказка
-
Ухил\(m=Δy/Δx\).
- Відповідь на
-
\(m=1/2\).
- Відповідь б
-
Точково-похила форма є\(y−4=\dfrac{1}{2}(x−1)\).
- Відповідь c
-
Форма нахилу-перехоплення є\(y=\dfrac{1}{2}x+\dfrac{7}{2}\).
Джессіка залишає свій будинок о 5:50 ранку і йде на 9-мильний пробіг. Вона повертається до свого будинку о 7:08 ранку Відповідайте на наступні питання, припускаючи, що Джессіка біжить в постійному темпі.
- Опишіть відстань\(D\) (у милі) Джессіка пробігає як лінійну функцію її часу виконання\(t\) (у хвилинах).
- Намалюйте графік\(D\).
- Тлумачити значення ухилу.
Рішення
а У той час\(t=0\) Джессіка знаходиться у своєму будинку, так що\(D(0)=0\). У\(t=78\) хвилини часу, Джессіка закінчив бігати\(9\) ми, так що\(D(78)=9\). Нахил лінійної функції дорівнює
\[m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber \]
\(y\)-перехоплення є\((0,0)\), тому рівняння для цієї лінійної функції є
\[D(t)=\dfrac{3}{26}t. \nonumber \]
б. для\(D\) графування використовують той факт, що графік проходить через початок і має нахил\(m=3/26.\)
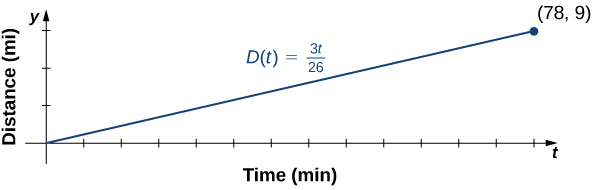
c Схил\(m=3/26≈0.115\) описує відстань (в милі) Джессіка пробігає за хвилину, або її середню швидкість.
Поліноми
Лінійна функція - це особливий тип більш загального класу функцій: поліноми. Поліноміальна функція - це будь-яка функція, яку можна записати у вигляді
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0 \nonumber \]
для деяких цілих\(n≥0\) і констант\(a_n,a_{n−1},…,a_0\), де\(a_n≠0\). У разі коли\(n=0\), ми дозволяємо for\(a_0=0\); if\(a_0=0\), функція\(f(x)=0\) називається нульовою функцією. Величина\(n\) називається ступенем многочлена; постійна\(a_n\) називається провідним коефіцієнтом. Лінійною функцією виду\(f(x)=mx+b\) є поліном ступеня 1 if\(m≠0\) і ступеня 0 if\(m=0\). Многочлен ступеня 0 також називається постійною функцією. Поліноміальна функція 2 ступеня називається квадратичною функцією. Зокрема, квадратична функція має вигляд
\[f(x)=ax^2+bx+c, \nonumber \]
де\(a≠0\). Поліноміальна функція ступеня\(3\) називається кубічною функцією.
Функції живлення
Деякі поліноміальні функції є силовими функціями. Функція потужності - це будь-яка функція виду\(f(x)=ax^b\), де\(a\) і\(b\) є будь-якими дійсними числами. Показником у степеневої функції може бути будь-яке дійсне число, але тут ми розглянемо випадок, коли показник є натуральним числом. (Інші випадки ми розглянемо пізніше.) Якщо експонента є натуральним числом, то\(f(x)=ax^n\) є поліном. Якщо\(n\) навіть, то\(f(x)=ax^n\) є парною функцією, тому\(n\) що\(f(−x)=a(−x)^n=ax^n\) якщо навіть. Якщо\(n\) непарна, то\(f(x)=ax^n\) є непарною функцією, тому що\(f(−x)=a(−x)^n=−ax^n\) якщо\(n\) непарна (Рисунок\(\PageIndex{4}\)).
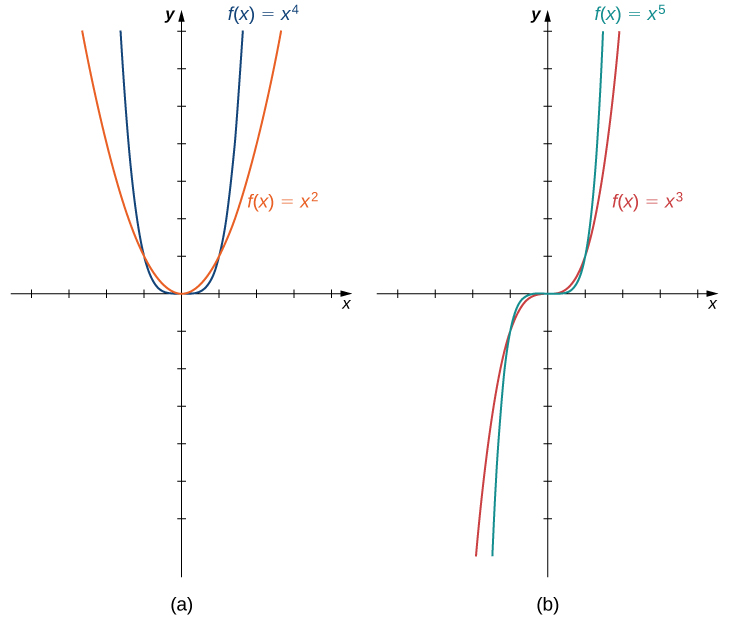
Поведінка на нескінченності
Щоб визначити поведінку функції, коли входи\(f\) наближаються до нескінченності, ми дивимося на значення,\(f(x)\) як входи\(x\), стають більшими. Для деяких функцій значення\(f(x)\) наближаються до скінченного числа. Наприклад, для функції\(f(x)=2+1/x\) значення\(1/x\) стають все ближче і ближче до нуля для всіх значень,\(x\) оскільки вони стають більшими і більшими. Для цієї функції ми говоримо «\(f(x)\)наближається до двох, як\(x\) йде до нескінченності», і ми пишемо\(f(x)→2\) як\(x→∞\). Лінія\(y=2\) є горизонтальною асимптотою функції,\(f(x)=2+1/x\) оскільки графік функції наближається до прямої та\(x\) стає більшою.
Для інших функцій значення\(f(x)\) можуть не наближатися до кінцевого числа, але замість цього можуть стати більшими для всіх значень,\(x\) оскільки вони стають більшими. У такому випадку ми говоримо «\(f(x)\)наближається до нескінченності як\(x\) наближається до нескінченності», і пишемо\(f(x)→∞\) як\(x→∞\). Наприклад, для функції виходи\(f(x)\) стають більшими\(f(x)=3x^2\), оскільки входи\(x\) стають більшими. Можна зробити висновок, що функція\(f(x)=3x^2\) наближається до нескінченності як\(x\) наближається до нескінченності, і\(3x^2→∞\) пишемо\(x→∞\) Поведінка як\(x→−∞\) і значення\(f(x)→−∞\) як\(x→∞\) або\(x→−∞\) можуть бути визначені аналогічно. Ми можемо описати, що відбувається зі значеннями\(f(x)\) як\(x→∞\) і\(x→−∞\) як кінцева поведінка функції.
Щоб зрозуміти поведінку кінця поліноміальних функцій, ми можемо зосередитись на квадратичних та кубічних функціях. Поведінка для поліномів вищого ступеня може бути проаналізована аналогічно. Розглянемо квадратичну функцію\(f(x)=ax^2+bx+c\). Якщо\(a>0\), то значення\(f(x)→∞\) як\(x→±∞\). Якщо\(a<0\), то значення\(f(x)→−∞\) як\(x→±∞\). Оскільки графік квадратичної функції є параболою, парабола відкривається вгору, якщо\(a>0\).; парабола відкривається вниз if\(a<0\) (рис.\(\PageIndex{5a}\)).
Тепер розглянемо кубічну функцію\(f(x)=ax^3+bx^2+cx+d\). Якщо\(a>0\), то\(f(x)→∞\) як\(x→∞\) і\(f(x)→−∞\) як\(x→−∞\). Якщо\(a<0\), то\(f(x)→−∞\) як\(x→∞\) і\(f(x)→∞\) як\(x→−∞\). Як ми бачимо з обох цих графіків, провідний член многочлена визначає кінцеву поведінку (рис.\(\PageIndex{5b}\)).
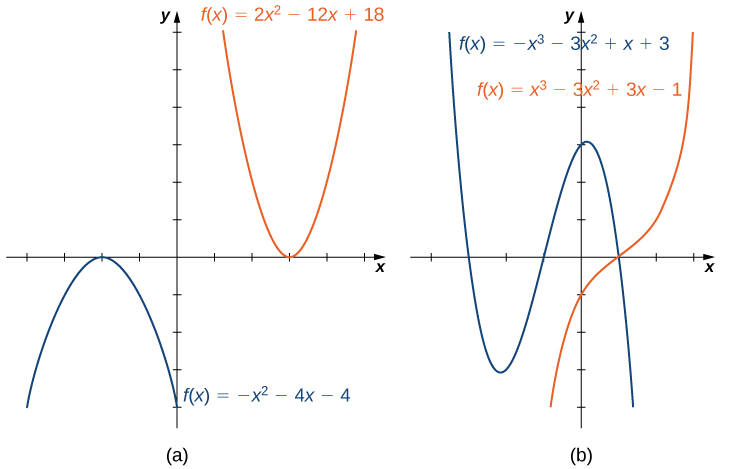
Нулі поліноміальних функцій
Ще однією характеристикою графіка поліноміальної функції є те, де він перетинає\(x\) -вісь. Щоб визначити, де функція\(f\) перетинає\(x\) -вісь, нам потрібно вирішити рівняння\(f(x)=0\) для\(x\). У випадку з лінійною функцією\(f(x)=mx+b\)\(x\) -перехоплення задається вирішенням рівняння\(mx+b=0\). У цьому випадку ми бачимо, що\(x\) -перехоплення задається\((−b/m,0)\). У випадку квадратичної функції знаходження\(x\) -перехоплення (ів) вимагає знаходження нулів квадратного рівняння:\(ax^2+bx+c=0\). У деяких випадках легко розрахувати многочлен,\(ax^2+bx+c\) щоб знайти нулі. Якщо ні, ми використовуємо квадратичну формулу.
Розглянемо квадратне рівняння
\[ax^2+bx+c=0, \nonumber \]
де\(a≠0\). Розв'язки цього рівняння задаються квадратичною формулою
\[x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}. \label{quad} \]
Якщо дискримінант\(b^2−4ac>0\), Equation\ ref {quad} повідомляє нам, що є два дійсних числа, які задовольняють квадратному рівнянню. Якщо\(b^2−4ac=0\), ця формула говорить нам, що існує тільки одне рішення, і це дійсне число. Якщо\(b^2−4ac<0\), ніякі дійсні числа не задовольняють квадратному рівнянню.
У випадку поліномів вищого ступеня може бути складніше визначити, де графік перетинає\(x\) вісь -. У деяких випадках можна знайти\(x\) -перехоплення шляхом факторингу полінома, щоб знайти його нулі. В інших випадках неможливо обчислити точні значення\(x\) -перехоплень. Однак, як ми бачимо пізніше в тексті, у таких випадках ми можемо використовувати аналітичні інструменти для наближення (до дуже високого ступеня), де розташовані\(x\) -перехоплення. Тут ми зосередимося на графіках поліномів, для яких ми можемо явно обчислити їх нулі.
Для наступних функцій,
- \(f(x)=−2x^2+4x−1\)
- \(f(x)=x^3−3x^2−4x\)
- опишіть поведінку\(f(x)\) як\(x→±∞\),
- знайти всі нулі\(f\), і
- ескіз графіка\(f\).
Рішення
1. Функція\(f(x)=−2x^2+4x−1\) являє собою квадратичну функцію.
1. Тому що\(a=−2<0\), як\(x→±∞,f(x)→−∞.\)
2. Щоб знайти нулі\(f\), використовуйте квадратичну формулу. Нулі є
\(x=\dfrac{−4±\sqrt{4^2−4(−2)(−1)}}{2(−2)}=\dfrac{−4±\sqrt{8}}{−4}=\dfrac{−4±2\sqrt{2}}{−4}=\dfrac{2±\sqrt{2}}{2}.\)
3. Щоб намалювати графік\(f\), використовуйте інформацію з ваших попередніх відповідей і об'єднайте її з тим, що графік є параболою, що відкривається вниз.
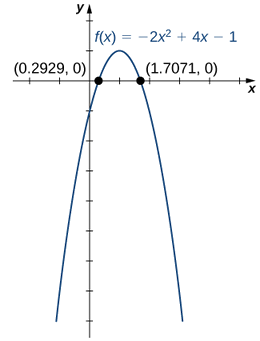
2. Функція\(f(x)=x^3−3x^2−4x\) є кубічною функцією.
1. Тому що\(a=1>0\), як\(x→∞\),\(f(x)→∞\). Як\(x→−∞\),\(f(x)→−∞\).
2. Щоб знайти нулі\(f\), нам потрібно множити многочлен. По-перше, коли ми\(x\) враховуємо всі терміни, ми знаходимо
\(f(x)=x(x^2−3x−4).\)
Потім, коли ми множимо квадратичну функцію\(x^2−3x−4\), ми знаходимо
\(f(x)=x(x−4)(x+1).\)
Тому нулі від\(f\) є\(x=0,4,−1\).
3. Поєднуючи результати з частин i. і ii., намалюйте приблизний ескіз\(f\).
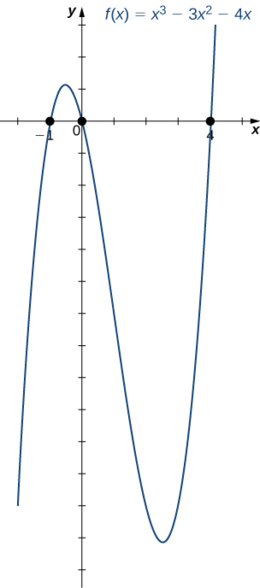
Розглянемо квадратичну функцію\(f(x)=3x^2−6x+2.\) Знайти нулі\(f\). Парабола відкривається вгору або вниз?
- Підказка
-
Використовуйте квадратичну формулу.
- Відповідь
-
Нулі є\(x=1±\sqrt{3}/3\). Парабола відкривається вгору.
Математичні моделі
Велика різноманітність реальних ситуацій можна описати за допомогою математичних моделей. Математична модель - це метод моделювання реальних ситуацій за допомогою математичних рівнянь. Фізики, інженери, економісти та інші дослідники розробляють моделі, поєднуючи спостереження з кількісними даними для розробки рівнянь, функцій, графіків та інших математичних інструментів для точного опису поведінки різних систем. Моделі корисні, оскільки вони допомагають прогнозувати майбутні результати. Приклади математичних моделей включають вивчення динаміки населення, дослідження погодних умов та прогнози продажів продукції.
Як приклад розглянемо математичну модель, яку компанія могла б використовувати для опису своєї виручки від продажу того чи іншого предмета. Сума виручки\(R\), яку компанія отримує від продажу проданих\(n\) предметів за ціною\(p\) доларів за одиницю, описується рівнянням\(R=p⋅n\). Компанію цікавить, як змінюються продажі в міру зміни ціни товару. Припустимо, що дані в таблиці\(\PageIndex{1}\) показують кількість одиниць, які компанія продає, як функція ціни за товар.
| \(p\) | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|
| \(n\) | 19.4 | 18,5 | 16.2 | 13,8 | 12.2 |
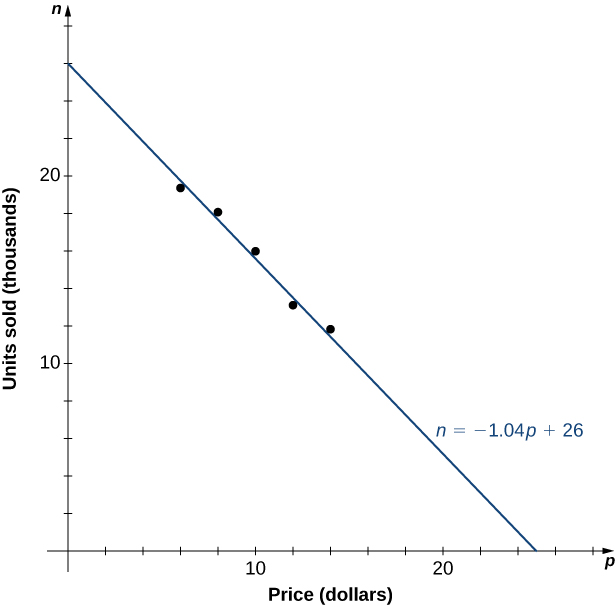
На малюнку\(\PageIndex{6}\) ми бачимо графік кількості проданих одиниць (в тисячах) в залежності від ціни (в доларах). Відзначимо з форми графіка, що кількість проданих одиниць, швидше за все, є лінійною функцією ціни на предмет, і дані можуть бути близько наближені лінійною функцією\(n= −1.04p+26\) для\(0≤p≤25\), де\(n\) прогнозується кількість одиниць, проданих тисячами. Використовуючи цю лінійну функцію, дохід (в тисячах доларів) можна оцінити квадратичною функцією
\[R(p)=p⋅ (−1.04p+26)=−1.04p^2+26p \text{ for }0≤p≤25. \nonumber \]
У прикладі\(\PageIndex{4}\) ми використовуємо цю квадратичну функцію для прогнозування суми доходу, яку компанія отримує залежно від ціни, яку компанія стягує за товар. Зверніть увагу, що ми не можемо остаточно укласти фактичну кількість одиниць, проданих за цінностями\(p\), для яких дані не збираються. Однак, враховуючи інші значення даних та показаний графік, здається розумним, що кількість проданих одиниць (у тисячах), якщо ціна стягується, становить\(p\) долари, може бути близькою до значень, передбачених лінійною функцією\(n=−1.04p+26.\)
Компанія зацікавлена в прогнозуванні суми доходу, яку вона отримає залежно від ціни, яку вона стягує за конкретний товар. Використовуючи дані з таблиці\(\PageIndex{1}\), компанія приходить до наступної квадратичної функції для моделювання доходу\(R\) як функції ціни на товар\(p:\)
\[R(p)=p⋅(−1.04p+26)=−1.04p^2+26p \nonumber \]
для\(0≤p≤25\).
- Прогнозуйте дохід, якщо компанія продає товар за ціною\(p=$5\) і\(p=$17\).
- Знайдіть нулі цієї функції і інтерпретуйте значення нулів.
- Намалюйте графік\(R\).
- Використовуйте графік, щоб визначити величину\(p\), яка максимізує дохід. Знайдіть максимальний дохід.
Рішення
а. оцінюючи функцію доходу при\(p=5\) і\(p=17\), можна зробити висновок, що
\(R(5)=−1.04(5)^2+26(5)=104,\text{ so revenue}=$104,000;\)
\(R(17)=−1.04(17)^2+26(17)=141.44,\text{ so revenue}=$141,440.\)
б. нулі цієї функції можна знайти, вирішивши рівняння\(−1.04p^2+26p=0\). Коли ми множимо квадратичний вираз, ми отримуємо\(p(−1.04p+26)=0\). Розв'язки цього рівняння наведені шляхом\(p=0,25\). Для цих значень\(p\) виручка дорівнює нулю. Коли\(p=$0\) дохід дорівнює нулю, оскільки компанія безкоштовно роздає свої товари. Коли\(p=$25\), дохід дорівнює нулю, тому що ціна занадто висока, і ніхто не буде купувати будь-які предмети.
c. знаючи той факт, що функція квадратична, ми також знаємо, що графік є параболою. Так як провідний коефіцієнт негативний, парабола відкривається вниз. Однією з властивостей парабол є те, що вони симетричні щодо осі симетрії, тому оскільки нулі знаходяться в\(p=0\) і\(p=25\), парабола повинна бути симетричною щодо лінії на півдорозі між ними, або\(p=12.5\).
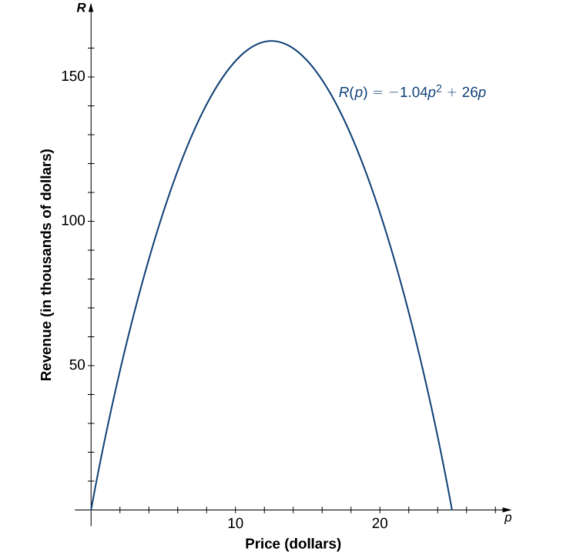
d Функція є параболою з нулями в\(p=0\) і\(p=25\), і вона симетрична щодо лінії\(p=12.5\), тому максимальний дохід відбувається за ціною за\(p=$12.50\) одиницю. За такою ціною дохід становить\(R(p)=−1.04(12.5)^2+26(12.5)=$162,500.\)
Алгебраїчні функції
Допускаючи частки та дробові степені в поліноміальних функціях, ми створюємо більший клас функцій. Алгебраїчна функція - це функція, яка передбачає додавання, віднімання, множення, ділення, раціональні сили та коріння. Два типи алгебраїчних функцій - це раціональні функції та кореневі функції.
Так само, як раціональні числа є частками цілих чисел, раціональні функції є частками многочленів. Зокрема, раціональна функція - це будь-яка функція виду\(f(x)=p(x)/q(x)\), де\(p(x)\) і\(q(x)\) є поліномами. Наприклад,
\(f(x)=\dfrac{3x−1}{5x+2}\)і\(g(x)=\dfrac{4}{x^2+1}\)
є раціональними функціями. Коренева функція - це потужна функція виду\(f(x)=x^{1/n}\), де\(n\) додатне ціле число більше одиниці. Наприклад,\(f(x)=x^{1/2}=\sqrt{x}\) є функцією квадратного кореня і\(g(x)=x^{1/3}=\sqrt[3]{x}\) є функцією cube-root. Допускаючи композиції кореневих функцій і раціональних функцій, ми можемо створювати інші алгебраїчні функції. Наприклад,\(f(x)=\sqrt{4−x^2}\) це алгебраїчна функція.
Для кожної з наступних функцій знайдіть домен і діапазон.
- \(f(x)=\dfrac{3x−1}{5x+2}\)
- \(f(x)=\sqrt{4−x^2}\)
Рішення
1. Ділити на нуль неможливо, тому домен - це набір дійсних чисел\(x\) такий, що\(x≠−2/5\). Щоб знайти діапазон, нам потрібно знайти значення,\(y\) для яких існує дійсне число\(x\) таке, що
\(y=\dfrac{3x−1}{5x+2}\)
Коли ми множимо обидві сторони цього рівняння на\(5x+2\), ми бачимо, що\(x\) має задовольняти рівняння
\(5xy+2y=3x−1.\)
З цього рівняння ми бачимо, що\(x\) повинно задовольняти
\(2y+1=x(3−5y).\)
Якщо y=\(3/5\), це рівняння не має розв'язку. З іншого боку, до тих пір\(y≠3/5\),
\(x=\dfrac{2y+1}{3−5y}\)
задовольняє цьому рівнянню. Можна зробити висновок, що асортимент\(f\) є\(\{y\,|\,y≠3/5\}\).
2. Щоб знайти домен\(f\), нам потрібно\(4−x^2≥0\). Коли ми враховуємо, ми пишемо\(4−x^2=(2−x)(2+x)≥0\). Ця нерівність тримається тоді і лише тоді, коли обидва терміни позитивні або обидва терміни негативні. Щоб обидва терміни були позитивними, нам потрібно знайти\(x\) таке, що
\(2−x≥0\)і\(2+x≥0.\)
Ці дві нерівності зводяться до\(2≥x\) і\(x≥−2\). Тому набір\(\{x\,|\,−2≤x≤2\}\) повинен бути частиною домену. Щоб обидва терміни були негативними, нам потрібно
\(2−x≤0\)і\(2+x\le 0.\)
Ці дві нерівності також зводяться до\(2≤x\) і\(x\le −2\). Немає значень\(x\), які задовольняють обидві ці нерівності. Таким чином, можна зробити висновок, що область цієї функції є\(\{x\,|\,−2≤x≤2\}.\)
Якщо\(−2≤x≤2\), то\(0≤4−x^2≤4\). \(0≤\sqrt{4−x2}≤2\)Тому і асортимент\(f\) - це\(\{y\,|\,0≤y≤2\}.\)
Пошук домену та діапазону для функції\(f(x)=(5x+2)/(2x−1).\)
- Підказка
-
Знаменник не може бути нулем. Розв'яжіть рівняння\(y=(5x+2)/(2x−1)\)\(x\) для пошуку діапазону.
- Відповідь
-
Домен - це набір дійсних чисел,\(x\) таких що\(x≠1/2\). Діапазон - набір\(\{y\,|\,y≠5/2\}\).
Кореневі функції\(f(x)=x^{1/n}\) мають визначальні характеристики залежно від того,\(n\) непарні чи парні. Для всіх парних цілих\(n≥2\) чисел доменом\(f(x)=x^{1/n}\) є інтервал\([0,∞)\). Для всіх непарних\(n≥1\) цілих чисел домен\(f(x)=x^{1/n}\) - це множина всіх дійсних чисел. Оскільки\(x^{1/n}=(−x)^{1/n}\) для непарних цілих чисел\(n\),\(f(x)=x^{1/n}\) є непарною функцією якщо\(n\) непарна. Див. графіки кореневих функцій для різних значень\(n\) на рис\(\PageIndex{7}\).
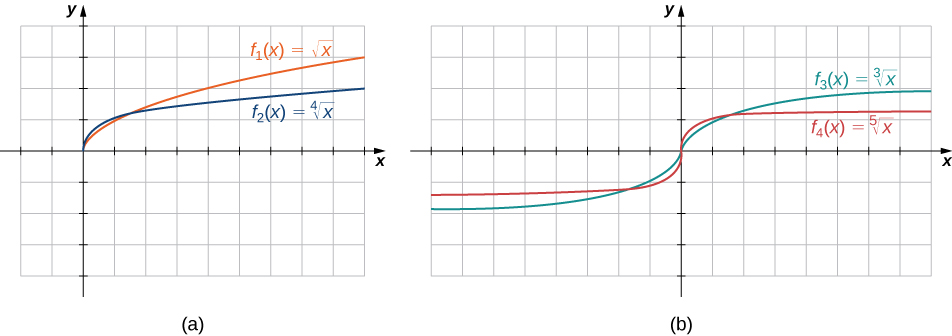
Для кожної з наступних функцій визначте область функції.
- \(f(x)=\dfrac{3}{x^2−1}\)
- \(f(x)=\dfrac{2x+5}{3x^2+4}\)
- \(f(x)=\sqrt{4−3x}\)
- \(f(x)=\sqrt[3]{2x−1}\)
Рішення
- Ви не можете розділити на нуль, тому домен - це набір значень\(x\) таких, що\(x^2−1≠0\). Тому домен є\(\{x\,|\,x≠±1\}\).
- Потрібно визначити значення,\(x\) для яких знаменник дорівнює нулю. Так як\(3x^2+4≥4\) для всіх дійсних\(x\) чисел знаменник ніколи не дорівнює нулю. Тому домен є\((−∞,∞).\)
- Оскільки квадратний корінь від'ємного числа не є дійсним числом, домен - це набір значень\(x\) для якого\(4−3x≥0\). Тому домен є\(\{x\,|\,x≤4/3\}.\)
- Корінь куба визначається для всіх дійсних чисел, тому домен є інтервалом\((−∞, ∞).\)
Знайдіть домен для кожної з наступних функцій:\(f(x)=(5−2x)/(x^2+2)\) і\(g(x)=\sqrt{5x−1}\).
- Підказка
-
Визначте значення,\(x\) коли вираз в знаменнику від\(f\) ненульовий, і знайдіть значення,\(x\) коли вираз всередині радикала of\(g\) є невід'ємним.
- Відповідь
-
Домен\(f\) is\((−∞, ∞)\). Домен\(g\) is\(\{x\,|\,x≥1/5\}.\)
Трансцендентні функції
Поки що ми обговорювали алгебраїчні функції. Деякі функції, однак, не можуть бути описані основними алгебраїчними операціями. Ці функції відомі як трансцендентні функції, тому що вони кажуть, що вони «перевершують» або виходять за рамки алгебри. Найпоширенішими трансцендентними функціями є тригонометричні, експоненціальні та логарифмічні функції. Тригонометрична функція пов'язує співвідношення двох сторін прямокутного трикутника. Вони\(\sin x, \cos x, \tan x, \cot x, \sec x,\text{ and }\csc x.\) (Ми обговорюємо тригонометричні функції пізніше в розділі.) Експоненціальна функція - це функція виду\(f(x)=b^x\), де знаходиться основа\(b>0,\, b≠1\). Логарифмічна функція - це функція виду\(f(x)=\log_b(x)\) для деякої константи\(b>0,\,b≠1,\), де\(\log_b(x)=y\) якщо і тільки якщо\(b^y=x\). (Ми також обговорюємо експоненціальні та логарифмічні функції пізніше в розділі.)
Класифікуйте кожну з наступних функцій, a. через c., як алгебраїчну або трансцендентну.
- \(f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}\)
- \(f(x)=2^{x^2}\)
- \( f(x)=\sin(2x)\)
Рішення
- Оскільки ця функція включає лише основні алгебраїчні операції, це алгебраїчна функція.
- Цю функцію не можна записати як формулу, яка включає лише основні алгебраїчні операції, тому вона трансцендентна. (Зверніть увагу, що алгебраїчні функції можуть мати лише повноваження, які є раціональними числами.)
- Як і в частині b, цю функцію неможливо записати за допомогою формули, яка включає лише основні алгебраїчні операції; отже, ця функція є трансцендентною.
Алгебраїчна чи трансцендентна функція?\(f(x)=x/2\)
- Відповідь
-
алгебраїчна
Кусково визначені функції
Іноді функція визначається різними формулами на різних ділянках своєї області. Функція з цією властивістю відома як кусково визначена функція. Функція абсолютного значення є прикладом кусково визначеної функції, оскільки формула змінюється зі знаком\(x\):
\[f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}. \nonumber \]
Інші кусково визначені функції можуть бути представлені абсолютно різними формулами, в залежності від частини області, в яку потрапляє точка. Для графіку кусково визначеної функції ми графуємо кожну частину функції у відповідній області, на тій же системі координат. Якщо формула для функції відрізняється для\(x<a\) і\(x>a\), нам потрібно звернути особливу увагу на те, що відбувається\(x=a\) при графіку функції. Іноді графік повинен включати розімкнуте або замкнуте коло, щоб вказати значення функції в\(x=a\). Ми розглянемо це в наступному прикладі.
Намалюйте графік наступної кусково визначеної функції:
\[f(x)=\begin{cases}x+3, & \text{if } x<1\\(x−2)^2, & \text{if } x≥1\end{cases} \nonumber \]
Рішення
Графік лінійної функції\(y=x+3\) на інтервалі\((−∞,1)\) і графік квадратичної функції\(y=(x−2)^2\) на інтервалі\([1,∞)\). Оскільки значення функції at\(x=1\) задається формулою\(f(x)=(x−2)^2\), ми бачимо, що\(f(1)=1\). Щоб позначити це на графіку, малюємо замкнуте коло в точці\((1,1)\). Значення функції задається\(f(x)=x+3\) for all\(x<1\), але не at\(x=1\). Щоб позначити це на графіку, малюємо розімкнуте коло при\((1,4)\).
2) Намалюйте графік функції
\(f(x)=\begin{cases}2−x, & \text{if } x≤2\\x+2, & \text{if } x>2\end{cases}.\)
Рішення:
2.Функція має x перехоплення в (2, 0) і y перехоплення в (0, 2)." src="https://math.libretexts.org/@api/dek...8509006001.png">
У великому місті з водіїв стягуються змінні тарифи за паркування в гаражі. Вони стягуються 10 доларів за першу годину або будь-яку частину першої години та додаткові $2 за кожну годину або її частину до максимум 30 доларів за день. Гараж працює з 6 ранку до 12 півночі.
- Напишіть кусково визначену функцію, яка описує вартість\(C\) паркування в гаражі як функцію годин, припаркованих\(x\).
- Намалюйте графік цієї функції\(C(x).\)
Рішення
1. Оскільки гараж працює по 18 годин щодня, домен для цієї функції є\(\{x\,|\,0<x≤18\}\). Вартість паркування автомобіля на цьому гаражі може бути описана кусково функцією
\[C(x)=\begin{cases}10, & \text{for } 0<x≤1\\12, & \text{for } 1<x≤2\\14, & \text{for } 2<x≤3\\16, & \text{for } 3<x≤4\\ ⋮\\30, & \text{for } 10<x≤18\end{cases}. \nonumber \]
2. Графік функції складається з декількох горизонтальних відрізків лінії.
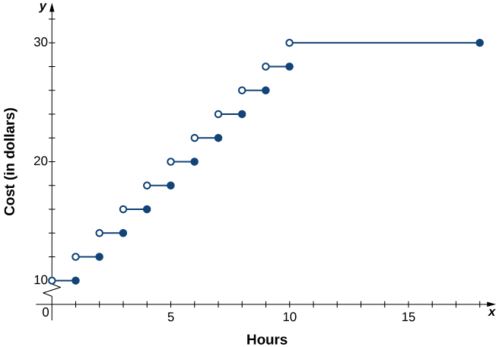
Вартість розсилки листа - це функція ваги листа. Припустимо, вартість розсилки листа\(49¢\) припадає на першу унцію і\(21¢\) за кожну додаткову унцію. Напишіть кусково визначену функцію, що описує вартість\(C\) як функцію ваги\(x\) для\(0<x≤3\), де\(C\) вимірюється в центах і\(x\) вимірюється в унціях.
- Підказка
-
Кусково визначена функція постійна на інтервалах\((0,1],\,(1,2],\,….\)
- Відповідь
-
\[C(x)=\begin{cases}49, 0<x≤1\\70, 1<x≤2\\91, 2<x≤3\end{cases} \nonumber \]
Перетворення функцій
Ми бачили кілька випадків, коли ми додавали, віднімали або множили константи, щоб сформувати варіації простих функцій. Наприклад, у попередньому прикладі ми віднімали 2 з аргументу функції,\(y=x^2\) щоб отримати функцію\(f(x)=(x−2)^2\). Це віднімання являє собою зсув функції\(y=x^2\) на дві одиниці вправо. Зсув, горизонтально або вертикально, є різновидом перетворення функції. Інші перетворення включають горизонтальне та вертикальне масштабування та відображення про осі.
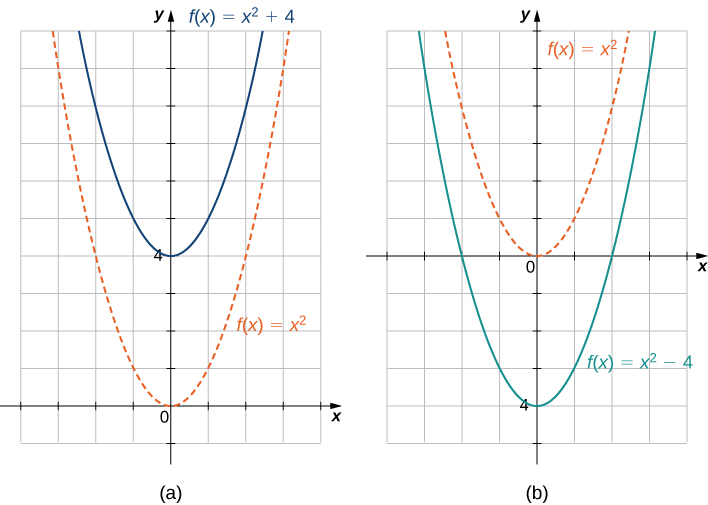
Вертикальний зсув функції відбувається, якщо ми додаємо або віднімаємо однакову константу до кожного виходу\(y\). Для\(c>0\), графік\(f(x)+c\) - це зсув графіка\(f(x)\) вгору\(c\) одиниць, тоді як графік\(f(x)−c\) - це зсув графіка\(c\) одиниць\(f(x)\) вниз. Наприклад, графік функції\(f(x)=x^3+4\) - це графік зсунутих вгору\(y=x^3\)\(4\) одиниць; графік функції\(f(x)=x^3−4\) - графік зсунутих вниз\(y=x^3\)\(4\) одиниць (рис.\(\PageIndex{9}\)).
Горизонтальний зсув функції відбувається, якщо ми додаємо або віднімаємо однакову константу до кожного входу\(x\). Для\(c>0\), графік\(f(x+c)\) - це зсув графа\(f(x)\) вліво\(c\) одиниць; графік\(f(x−c)\) - це зсув графа\(f(x)\) вправо\(c\) одиниць. Чому графік зсувається вліво при додаванні константи і зрушення вправо при відніманні константи? Щоб відповісти на це питання, давайте розглянемо приклад.
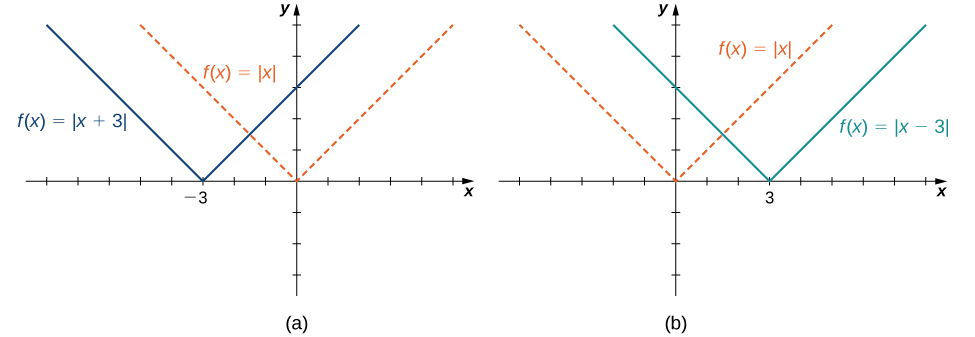
Розглянемо функцію\(f(x)=|x+3|\) і оцінюємо цю функцію на\(x−3\). Так як\(f(x−3)=|x|\) і\(x−3<x\), графік\(f(x)=|x+3|\) - це графік зсунутих\(y=|x|\) лівих\(3\) одиниць. Аналогічно графік\(f(x)=|x−3|\) - це графік\(y=|x|\) зсунутих правих\(3\) одиниць (рис.\(\PageIndex{10}\)).
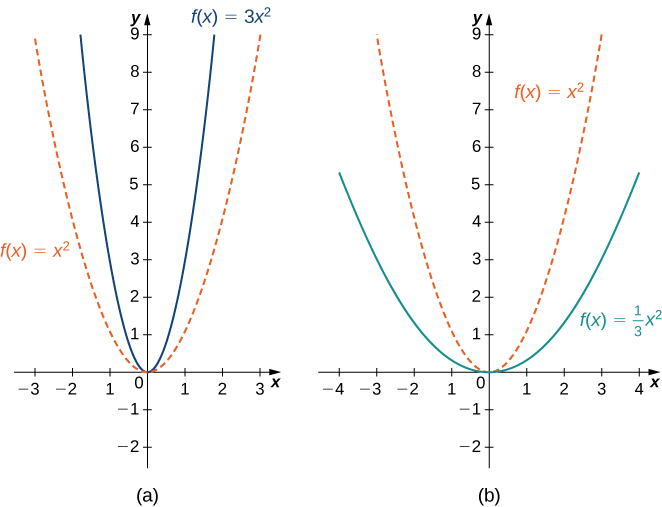
Вертикальне масштабування графіка відбувається, якщо ми помножимо всі виходи\(y\) функції на одну і ту ж позитивну константу. Для\(c>0\), графіком функції\(cf(x)\) є графік\(f(x)\) масштабованого по вертикалі в множник\(c\). Якщо\(c>1\), значення виходів для функції більше\(cf(x)\), ніж значення виходів для функції\(f(x)\); отже, графік був розтягнутий вертикально. Якщо\(0<c<1\), то виходи функції менше\(cf(x)\), тому графік був стиснутий. Наприклад, графік функції\(f(x)=3x^2\) - це графік\(y=x^2\) розтягнутої по вертикалі в 3 рази, тоді як графік\(f(x)=x^2/3\) - це графік\(y=x^2\) стисненого вертикально в множник\(3\) (рис.\(\PageIndex{11b}\)).
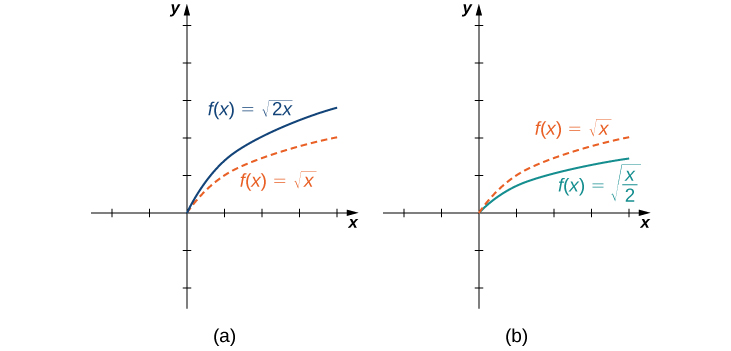
Горизонтальне масштабування функції відбувається, якщо ми помножимо входи\(x\) на ту саму позитивну константу. Для\(c>0\), графіком функції\(f(cx)\) є графік\(f(x)\) масштабованого по горизонталі в множник\(c\). Якщо\(c>1\), графік\(f(cx)\) є графіком\(f(x)\) стиснутого горизонтально. Якщо\(0<c<1\), графік\(f(cx)\) є графіком\(f(x)\) розтягнутої горизонталі. Наприклад, розглянемо функцію\(f(x)=\sqrt{2x}\) і оцінюємо\(f\) при\(x/2\). Так як\(f(x/2)=\sqrt{x}\), графік\(f(x)=\sqrt{2x}\) - це графік\(y=\sqrt{x}\) стиснутого по горизонталі. Графік\(y=\sqrt{x/2}\) є горизонтальним розтягненням графіка\(y=\sqrt{x}\) (рис.\(\PageIndex{12}\)).
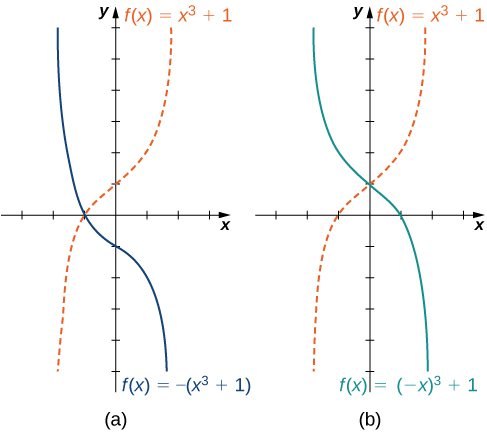
Ми вивчили, що відбувається з графіком функції,\(f\) коли ми множимо\(f\) на константу,\(c>0\) щоб отримати нову функцію\(cf(x)\). Ми також обговорили, що відбувається з графіком функції,\(f\) коли ми множимо незалежну змінну\(x\) на,\(c>0\) щоб отримати нову функцію\(f(cx)\). Однак ми не зверталися до того, що відбувається з графіком функції, якщо константа\(c\) негативна. Якщо у нас є константа\(c<0\), ми можемо записати\(c\) як додатне число, помножене на\(−1\); але, яке перетворення ми отримуємо, коли множимо функцію або її аргумент на\(−1?\) Коли ми множимо всі виходи на\(−1\), ми отримуємо відображення про\(x\) -осі. Коли ми помножимо всі входи на\(−1\), ми отримуємо відображення про\(y\) -осі. Наприклад, графік\(f(x)=−(x^3+1)\) - це графік\(y=(x^3+1)\) відбитого про\(x\) -осі. Графік\(f(x)=(−x)^3+1\) - це графік\(y=x^3+1\) відбитого близько\(y\) -осі (рис.\(\PageIndex{13}\)).
Якщо графік функції складається з декількох перетворень іншого графіка, важливо перетворити графік у правильному порядку. Задана функція\(f(x)\), графік пов'язаної функції\(y=cf(a(x+b))+d\) можна отримати з графіка,\(y=f(x)\) виконавши перетворення в наступному порядку.
- Горизонтальний зсув графіка\(y=f(x)\). Якщо\(b>0\), зрушуємо вліво. Якщо\(b<0\) зрушити вправо.
- Горизонтальне масштабування графіка\(y=f(x+b)\) на множник\(|a|\). Якщо\(a<0\), відобразити графік близько\(y\) -осі.
- Вертикальне масштабування графіка\(y=f(a(x+b))\) на множник\(|c|\). Якщо\(c<0\), відобразити графік близько\(x\) -осі.
- Вертикальний зсув графіка\(y=cf(a(x+b))\). Якщо\(d>0\), зрушити вгору. Якщо\(d<0\), зрушити вниз.
Ми можемо узагальнити різні перетворення та пов'язані з ними ефекти на графіку функції в наступній таблиці.
| Трансформація\(f (c>0)\) | Ефект від графіка\(f\) |
|---|---|
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(x)+c\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; "> Вертикальний зсув вгору\(c\) одиниць |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(x)-c\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; "> Вертикальний зсув вниз\(c\) одиниць |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(x+c)\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; "> Зсув ліворуч за\(c\) одиницями |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(x-c)\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; "> Зсув праворуч за\(c\) одиницями |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(cf(x)\) | \ (f\)» style="вертикальне вирівнювання: середина; ">
Вертикальна розтяжка якщо\(c>1\); вертикальне стиснення, якщо\(0<c<1\) |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(cx)\) | \ (f\)» style="вертикальне вирівнювання: середина; ">
Горизонтальна розтяжка якщо\(0<c<1\); горизонтальне стиснення, якщо\(c>1\) |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(-f(x)\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; ">Відображення навколо\(x\) осі - |
| \ (f (c> 0)\)» style="вирівнювання тексту: центр; вертикальне вирівнювання: середина; ">\(f(-x)\) | \ (f\)» style="text-align:center; вертикальне вирівнювання: middle; ">Відображення навколо\(y\) осі - |
Для кожної з наступних функцій a. і b., намалюйте графік, використовуючи послідовність перетворень відомої функції.
- \(f(x)=−|x+2|−3\)
- \(f(x)=\sqrt[3]{x}+1\)
Рішення
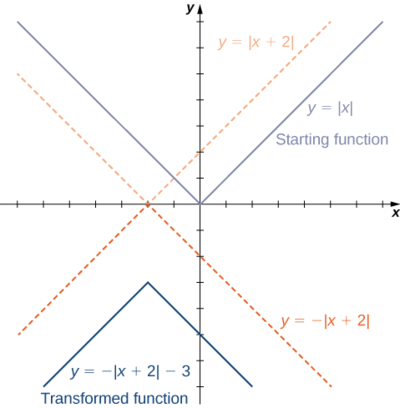
1. Починаючи з графіка\(y=|x|\), зсуваємо\(2\) одиниці вліво, відбиваємо близько\(x\) -осі, а потім зміщуємо\(3\) одиниці вниз.
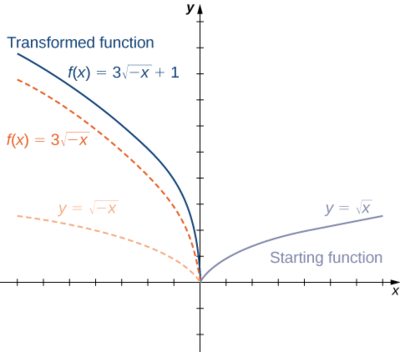
2. Починаючи з графіка\(y=sqrt{x},\) відображення близько\(y\) -осі, розтягніть графік по вертикалі в 3 рази, і перемістіть вгору на 1 одиницю.
Опишіть, як функція\(f(x)=−(x+1)^2−4\) може бути побудована графіком за допомогою графіка\(y=x^2\) і послідовності перетворень
- Відповідь
-
Зсуваємо графік\(y=x^2\) вліво на 1 одиницю, відбиваємо близько\(x\) -осі, потім зрушуємо вниз на 4 одиниці.
Ключові поняття
- Функція потужності\(f(x)=x^n\) є парною функцією, якщо n парна і\(n≠0\), і це непарна функція, якщо\(n\) непарна.
- Коренева функція\(f(x)=x^{1/n}\) має домен,\([0,∞)\) якщо n парний, а домен\((−∞,∞)\) якщо\(n\) непарний. Якщо\(n\) непарна, то\(f(x)=x^{1/n}\) є непарною функцією.
- Домен раціональної функції\(f(x)=p(x)/q(x)\), де\(p(x)\) і\(q(x)\) є поліноміальними функціями, є множина\(x\) таких, що\(q(x)≠0\).
- Функції, які передбачають основні операції додавання, віднімання, множення, ділення та степеней, є алгебраїчними функціями. Всі інші функції трансцендентні. Тригонометричні, експоненціальні та логарифмічні функції є прикладами трансцендентних функцій.
- Поліноміальна функція\(f\) зі ступенем\(n≥1\) задовольняє\(f(x)→±∞\) як\(x→±∞\). Знак виходу як\(x→∞\) залежить тільки від знака провідного коефіцієнта і від того,\(n\) парний чи непарний.
- Вертикальні і горизонтальні зсуви, вертикальні і горизонтальні масштабування, а також роздуми про\(x\) - і\(y\) -осі є прикладами перетворень функцій.
Ключові рівняння
- Рівняння точкового нахилу прямої\[y−y_1=m(x−x_1)\nonumber \]
- Ухил-перехоплення форми лінії\[y=mx+b\nonumber \]
- Стандартна форма лінії\[ax+by=c\nonumber \]
- Функція полінома\[f(x)=a_n{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber \]
Глосарій
- алгебраїчна функція
- функція, що включає будь-яку комбінацію лише основних операцій додавання, віднімання, множення, ділення, степенів та коренів, застосованих до вхідної змінної\(x\)
- кубічна функція
- многочлен ступеня 3; тобто функція виду\(f(x)=ax^3+bx^2+cx+d\), де\(a≠0\)
- ступінь
- для поліноміальної функції значення найбільшого показника будь-якого члена
- лінійна функція
- функція, яка може бути записана у формі\(f(x)=mx+b\)
- логарифмічна функція
- функція форми\(f(x)=\log_b(x)\) для деякої бази\(b>0,\,b≠1\) такі, що\(y=\log_b(x)\) якщо і тільки якщо\(b^y=x\)
- математична модель
- Метод моделювання реальних життєвих ситуацій за допомогою математичних рівнянь
- кусково визначена функція
- функція, яка визначається по-різному на різних ділянках своєї області
- рівняння точки-нахилу
- рівняння лінійної функції із зазначенням її нахилу і точки на графіку функції
- функція полінома
- функція форми\(f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0\)
- функція харчування
- функція виду\(f(x)=x^n\) для будь-якого додатного цілого числа\(n≥1\)
- квадратична функція
- многочлен ступеня 2; тобто функція форми,\(f(x)=ax^2+bx+c\) де\(a≠0\)
- раціональна функція
- функція виду\(f(x)=p(x)/q(x)\), де\(p(x)\) і\(q(x)\) є поліномами
- функція кореня
- функція виду\(f(x)=x^{1/n}\) для будь-якого цілого числа\(n≥2\)
- ухил
- зміна\(y\) для кожної одиниці зміни в\(x\)
- ухил-перехоплення форма
- рівняння лінійної функції із зазначенням її нахилу та\(y\) -перехоплення
- трансцендентна функція
- функція, яка не може бути виражена комбінацією основних арифметичних операцій
- перетворення функції
- зсув, масштабування або відображення функції
