16.2: Лінійні інтеграли

Цілі навчання

• Обчисліть скалярний інтеграл прямої вздовж кривої.
• Обчисліть інтеграл векторної лінії вздовж орієнтованої кривої в просторі.
• Використовуйте лінійний інтеграл для обчислення роботи, виконаної при переміщенні об'єкта вздовж кривої в векторному полі.
• Опишіть потік і циркуляцію векторного поля.

Ми знайомі з однозмінними інтегралами виду\(\displaystyle \int_{a}^{b}f(x)\,dx\), де областю інтеграції є інтервал\([a,b]\). Такий інтервал можна розглядати як криву в\(xy\) -площині, оскільки інтервал визначає відрізок лінії з кінцевими точками\((a,0)\) і\((b,0)\) —іншими словами, відрізок лінії, розташований на\(x\) -осі. Припустимо, ми хочемо інтегрувати над будь-якою кривою в площині, а не тільки над відрізком лінії на\(x\) -осі. Таке завдання вимагає нового виду інтеграла, званого лінійним інтегралом.

Лінійні інтеграли мають безліч застосувань в техніці та фізиці. Вони також дозволяють зробити кілька корисних узагальнень фундаментальної теореми числення. Причому, вони тісно пов'язані з властивостями векторних полів, як ми побачимо.

Скалярні лінійні інтеграли

Лінійний інтеграл дає нам можливість інтегрувати багатозмінні функції та векторні поля над довільними кривими в площині або в просторі. Існує два типи лінійних інтегралів: скалярні лінійні інтеграли та векторні лінійні інтеграли. Скалярні лінійні інтеграли є інтегралами скалярної функції над кривою в площині або в просторі. Векторні лінійні інтеграли є інтегралами векторного поля над кривою в площині або в просторі. Давайте спочатку розглянемо скалярні лінійні інтеграли.

Скалярний лінійний інтеграл визначається так само, як однозмінний інтеграл визначається, за винятком того, що для скалярного лінійного інтеграла integrand є функцією більше однієї змінної, а область інтеграції - крива в площині або в просторі, на відміну від кривої на\(x\) -осі.

Для скалярної лінії інтеграла, ми дозволяємо\(C\) бути гладкою кривою в площині або в просторі і нехай ff бути функція з доменом, який включає\(C\). Криву рубаємо на невеликі шматочки. Для кожного шматка ми вибираємо точку\(P\) в цій частині і оцінюємо\(f\) на\(P\). (Ми можемо зробити це, тому що всі точки на кривій знаходяться в області\(f\).) Множимо\(f(P)\) на довжину дуги шматка\(\Delta s\), складаємо виріб\(f(P)\Delta s\) по всіх шматках, а потім даємо довжині дуги шматочків зменшитися до нуля, взявши межу. Результатом є скалярний лінійний інтеграл функції над кривою.

Для формального опису скалярного лінійного інтеграла, нехай\(C\) буде плавна крива в просторі, задана параметризацією\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). \(f(x,y,z)\)Дозволяти функція з доменом, який включає криву\(C\). Щоб визначити лінійний інтеграл функції\(f\) над\(C\), ми починаємо, як починається більшість визначень інтеграла: ми рубаємо криву на дрібні шматочки. Розділити параметр інтервал\([a,b]\) на\(n\) підінтервали\([t_{i−l},t_i]\) однакової ширини for\(1≤i≤n\), де\(t_0=a\) і\(t_n=b\) (рис.\(\PageIndex{1}\)). \(t_{i}^*\)Дозволяти значення в\(i^{th}\) інтервалі\([t_{i−l},t_i]\). Позначте кінцеві точки\(\vecs r(t_0)\),\(\vecs r(t_1)\),...,\(\vecs r(t_n)\) по\(P_0\),...,\(P_n\). Точки P _i\(C\) ділять криву на\(n\) шматки\(C_1\)\(C_2\),,...\(C_n\),, з довжинами\(\Delta s_1\)\(\Delta s_2\),,...\(\Delta s_n\), відповідно. \(P_{i}^*\)Дозволяти позначити кінцеву точку\(\vecs r(t_{i}^*)\) for\(1≤i≤n\). Тепер ми оцінюємо функцію\(f\) в точці\(P_{i}^*\) для\(1≤i≤n\). Зверніть увагу, що\(P_{i}^*\) є поштучно\(C_1\), і тому\(P_{i}^*\) знаходиться в домені\(f\). \(f(P_{i}^*)\)Помножте на\(\Delta s_1\) довжину\(C_1\), яка дає площу «аркуша» з підставою\(C_1\), і висоту\(f(P_{i}^{*})\). Це аналогічно використанню прямокутників для наближення площі в однозмінному інтегралі. Тепер формуємо суму\(\displaystyle \sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i\).

Малюнок\(\PageIndex{1}\): Крива\(C\) була розділена на n частин, і була обрана точка всередині кожного шматка.

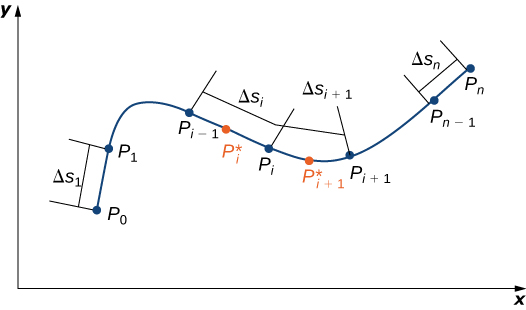
Зверніть увагу на подібність цієї суми з сумою Рімана; насправді це визначення є узагальненням суми Рімана до довільних кривих у просторі. Так само, як і з сумами Рімана та інтегралами форми\(\displaystyle \int_{a}^{b}g(x)\,dx\), ми визначаємо інтеграл, дозволяючи ширині шматків кривої зменшуватися до нуля, приймаючи межу. Результатом є скалярний лінійний інтеграл\(f\) уздовж\(C\).

Можливо, ви помітили різницю між цим визначенням скалярного лінійного інтеграла та однозмінного інтеграла. У цьому визначенні довжини дуги\(\Delta s_1\),\(\Delta s_2\),...,\(\Delta s_n\) не обов'язково однакові; при визначенні однозмінного інтеграла крива в\(x\) -осі розділена на шматки однакової довжини. Ця різниця не робить ніякого впливу на ліміт. Коли ми зменшуємо довжини дуги до нуля, їх значення стають досить близькими, що будь-яка невелика різниця стає неактуальною.

ВИЗНАЧЕННЯ: Скалярний інтеграл лінії

\(f\)Дозволяти функція з областю, яка включає плавну криву,\(C\) яка параметризується\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Скалярний прямий інтеграл від\(f\) along\(C\) дорівнює

\[\int_C f(x,y,z) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n}f(P_{i}^{*})\,\Delta s_i \label{eq12a} \]

якщо ця межа існує (\(t_i ^{*}\)і\(\Delta s_i\) визначаються як у попередніх параграфах). Якщо\(C\) це плоска крива, то\(C\) може бути представлена параметричними рівняннями\(x=x(t)\)\(y=y(t)\), і\(a≤t≤b\). Якщо\(C\) є гладким і\(f(x,y)\) є функцією двох змінних, то скалярний лінійний інтеграл\(f\) алонг\(C\) визначається аналогічно

\[\int_C f(x,y) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i, \label{eq13} \]

якщо ця межа існує.

Якщо\(f\) є безперервною функцією на плавній кривій\(C\), то\(\displaystyle \int_C f \,ds\) завжди існує. Оскільки\(\displaystyle \int_C f \,ds\) визначається як межа сум Рімана, безперервність\(f\) достатня, щоб гарантувати існування межі, так само, як інтеграл\(\displaystyle \int_{a}^{b}g(x)\,dx\) існує, якщо\(g\) він безперервний\([a,b]\).

Перш ніж дивитися на те, як обчислити лінійний інтеграл, нам потрібно вивчити геометрію, захоплену цими інтегралами. Припустимо, що\(f(x,y)≥0\) для всіх точок\((x,y)\) на плавній плоскій кривій\(C\). Уявіть, як взяти криву\(C\) і проектувати її «вгору» на поверхню\(f(x,y)\), визначену, тим самим створюючи нову криву\(C′\), яка лежить на графіку\(f(x,y)\) (рис.\(\PageIndex{2}\)). Тепер опускаємо «аркуш»\(C′\) вниз на\(xy\) -площину. Площа цього листа дорівнює\(\displaystyle \int_C f(x,y)ds\). Якщо\(f(x,y)≤0\) для деяких точок в\(C\), то значенням\(\displaystyle \int_C f(x,y)\,ds\) буде площа над\(xy\) -площиною менше площі нижче\(xy\) -площини. (Зверніть увагу на схожість з інтегралами виду\(\displaystyle \int_{a}^{b}g(x)\,dx\).)

Малюнок\(\PageIndex{2}\): Площа синього аркуша дорівнює\(\displaystyle \int_C f(x,y)\,ds\).

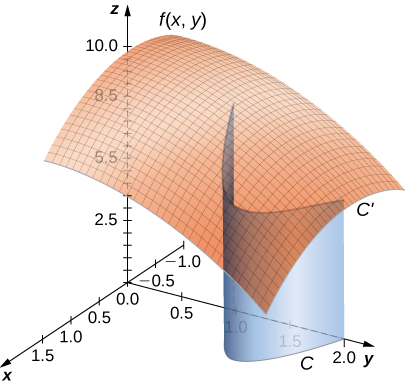
З цієї геометрії ми бачимо, що лінійний інтеграл\(\displaystyle \int_C f(x,y)\,ds\) не залежить від\(\vecs r(t)\) параметризації\(C\). Поки крива проходить рівно один раз параметризацією, площа листа, утвореного функцією та кривою, однакова. Цей же геометричний аргумент можна розширити, щоб показати, що лінійний інтеграл тризмінної функції над кривою в просторі не залежить від параметризації кривої.

Приклад\(\PageIndex{1}\): ​​​​​​Finding the Value of a Line Integral

Знайти значення інтеграла\(\displaystyle \int_C 2\,ds\), де\(C\) верхня половина одиничного кола.

Рішення

Цілісний є\(f(x,y)=2\). На малюнку\(\PageIndex{3}\) показаний графік\(f(x,y)=2\), крива С, і сформований ними лист. Зверніть увагу, що цей лист має ту ж площу, що і прямокутник з шириною\(\pi\) і довжиною\(2\). Тому,\(\displaystyle \int_C 2 \,ds=2\pi\,\text{units}^2\).

Малюнок\(\PageIndex{3}\): Лист, який утворений верхньою половиною одиничного кола в площині і графіком\(f(x,y)=2\).

Щоб побачити, що\(\displaystyle \int_C 2 \,ds=2\pi\) за допомогою визначення лінійного інтеграла, ми дозволимо\(\vecs r(t)\) бути параметризація\(C\). Потім,\(f(\vecs r(t_i))=2\) для будь-якого числа\(t_i\) в домені домену\(\vecs r\). Тому,

\[\begin{align*} \int_C f \,ds &=\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_{i}^{*}))\,\Delta s_i \\[4pt] &=\lim_{n\to\infty}\sum_{i=1}^{n}2\,\Delta s_i \\[4pt] &=2\lim_{n\to\infty}\sum_{i=1}^{n}\,\Delta s_i \\[4pt] &=2(\text{length}\space \text{of}\space C) \\[4pt] &=2\pi \,\text{units}^2. \end{align*}\]

Вправа\(\PageIndex{1}\)

Знайти значення\(\displaystyle \int_C(x+y)\,ds\), де\(C\) крива параметризується\(x=t\),\(y=t\),\(0≤t≤1\).

Підказка

Знайти форму, утворену\(C\) і графік функції\(f(x,y)=x+y\).

Відповідь

\(\sqrt{2}\)

Зверніть увагу, що в скалярному лінійному інтегралі інтеграція здійснюється щодо довжини дуги\(s\), що може зробити інтеграл скалярної лінії важко обчислити. Щоб полегшити обчислення, ми можемо\(\displaystyle \int_C f\,ds\) перевести на інтеграл зі змінною інтеграції, тобто\(t\).

Нехай\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\) для\(a≤t≤b\) буде параметризація\(C\). Оскільки ми припускаємо, що\(C\) це гладко,\(\vecs r′(t)=⟨x′(t),y′(t),z′(t)⟩\) є безперервним для всіх\(t\) в\([a,b]\). Зокрема,,\(x′(t)\)\(y′(t)\), і\(z′(t)\) існують для всіх\(t\) в\([a,b]\). За формулою довжини дуги ми маємо

\[\text{length}(C_i)=\Delta s_i=\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt. \nonumber \]

Якщо ширина\(\Delta t_i=t_i−t_{i−1}\) невелика, то функція\(\displaystyle \int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_i^*)‖\,\Delta t_i\),\(‖\vecs r′(t)‖\) майже постійна протягом інтервалу\([t_{i−1},t_i]\). Тому,

\[\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_{i}^{*})‖\,\Delta t_i, \label{approxLineIntEq1} \]

і у нас є

\[\sum_{i=1}^{n} f(\vecs r(t_i^*))\,\Delta s_i\approx\sum_{i=1}^{n} f(\vecs r(t_{i}^{*})) ‖\vecs r′(t_{i}^{*})‖\,\Delta t_i. \nonumber \]

Див\(\PageIndex{4}\). Малюнок.

Малюнок\(\PageIndex{4}\): Якщо ми збільшимо криву достатньо, зробивши\(\Delta t_i\) дуже маленьку, то відповідний фрагмент кривої буде приблизно лінійним.

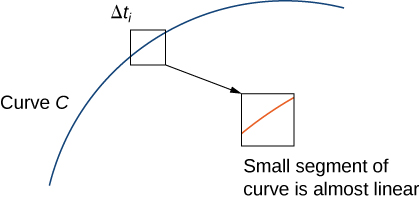
Зверніть увагу, що

\[\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_i^*))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i=\int_a^b f(\vecs r(t))‖\vecs r′(t)‖\,dt. \nonumber \]

Іншими словами, у міру зменшення ширини\([t_{i−1},t_i]\) інтервалів до нуля сума\(\displaystyle \sum_{i=1}^{n} f(\vecs r(t_i^{*}))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i\) сходиться до інтеграла\(\displaystyle \int_{a}^{b}f(\vecs r(t))‖\vecs r′(t)‖\,dt\). Тому маємо наступну теорему.

Теорема: Оцінка скалярного лінійного інтеграла

\(f\)Дозволяти безперервна функція з областю, яка включає плавну криву\(C\) з параметризацією\(\vecs r(t)\),\(a≤t≤b\). Тоді

\[\int_C f \,ds=\int_{a}^{b} f(\vecs r(t))‖\vecs r′(t)‖\,dt.\label{scalerLineInt1} \]

Хоча ми позначили Equation\ ref {ApproxLineInteq1} як рівняння, воно більш точно вважається наближенням, оскільки ми можемо показати, що ліва сторона Equation\ ref {ApproxLineInteq1} наближається до правої сторони як\(n\to\infty\). Іншими словами, дозволяючи ширині шматків зменшуватися до нуля робить праву суму довільно близькою до лівої суми. Так як

\[‖\vecs r′(t)‖=\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2}, \nonumber \]

отримаємо наступну теорему, яку використовуємо для обчислення скалярних лінійних інтегралів.

Теорема: Розрахунок інтеграла скалярної лінії

\(f\)Дозволяти безперервна функція з областю, яка включає плавну криву\(C\) з параметризацією\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Тоді

\[\int_C f(x,y,z) \,ds=\int_{a}^{b} f(\vecs r(t))\sqrt{({x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt. \nonumber \]

Аналогічно,

\[\int_C f(x,y) \,ds=\int_{a}^{b}f(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2} \,dt \nonumber \]

if\(C\) - плоска крива і\(f\) є функцією двох змінних.

Зауважимо, що наслідком цієї теореми є рівняння\(ds=‖\vecs r′(t)‖ \,dt\). Іншими словами, зміна довжини дуги можна розглядати як зміну в\(t\) -області, масштабовану величиною вектора\(\vecs r′(t)\).

Приклад\(\PageIndex{2}\): Evaluating a Line Integral

Знайти значення інтеграла\(\displaystyle \int_C(x^2+y^2+z) \,ds\),\(C\) де частина спіралі параметризується\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤2\pi\).

Рішення

Щоб обчислити скалярний лінійний інтеграл, ми починаємо з перетворення змінної інтеграції з довжини дуги\(s\) в\(t\). Потім ми можемо використовувати Equation\ ref {eq12a} для обчислення інтеграла щодо\(t\). Зверніть увагу, що

\[f(\vecs r(t))={\cos}^2 t+{\sin}^2 t+t=1+t \nonumber \]

і

\[\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} =\sqrt{{(−\sin(t))}^2+{\cos}^2(t)+1} =\sqrt{2}.\nonumber \]

Тому,

\[\int_C(x^2+y^2+z) \,ds=\int_{0}^{2\pi} (1+t)\sqrt{2} \,dt. \nonumber \]

Зверніть увагу, що Equation\ ref {eq12a} перевів оригінальний складний лінійний інтеграл в керований однозмінний інтеграл. Так як

\ [\ почати {вирівнювати*}\ int_ {0} ^ {2\ пі} (1+т)\ sqrt {2}\, dt &= {\ лівий [\ sqrt {2} t+\ dfrac {\ sqrt {2} t^2} {2}\ правий]} _ {0} ^ {2\ пі}\ [4pt]
&=2\ sqrt {2}\ pi+2\ sqrt {2} {\ pi} ^2,\ end {align*}\]

у нас є

\[\int_C(x^2+y^2+z) \,ds=2\sqrt{2}\pi+2\sqrt{2}{\pi}^2. \nonumber \]

Вправа\(\PageIndex{2}\)

Оцініть\(\displaystyle \int_C(x^2+y^2+z)ds\), де С - крива з параметризацією\(\vecs r(t)=⟨\sin(3t),\cos(3t)⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Підказка

Використовувати двозмінну версію скалярного лінійного інтегрального визначення (Equation\ ref {eq13}).

Відповідь

\[\dfrac{1}{3}+\dfrac{\sqrt{2}}{6}+\dfrac{3\pi}{4} \nonumber \]

Приклад\(\PageIndex{3}\): Independence of Parameterization

Знайти значення інтеграла\(\displaystyle \int_C(x^2+y^2+z) \,ds\),\(C\) де частина спіралі параметризується\(\vecs r(t)=⟨\cos(2t),\sin(2t),2t⟩\),\(0≤t≤π\). Зверніть увагу, що ця функція та крива такі ж, як у попередньому прикладі; єдина відмінність полягає в тому, що крива була перепараметризована так, що час працює вдвічі швидше.

Рішення

Як і в попередньому прикладі, ми використовуємо Equation\ ref {eq12a} для обчислення інтеграла відносно\(t\). Зверніть увагу, що\(f(\vecs r(t))={\cos}^2(2t)+{\sin}^2(2t)+2t=2t+1\) і

\ [\ почати {вирівнювати*}\ sqrt {{(x′ (t)))} ^2+ {(y′ (t))} ^2+ {(z′ (t)))} ^2} &=\ sqrt {(−\ sin t+\ cos t+4)}\\ [4pt] &=22
\ кінець {align*}\]

тому у нас є

\[\begin{align*} \int_C(x^2+y^2+z)ds &=2\sqrt{2}\int_{0}^{\pi}(1+2t)dt\\[4pt] &=2\sqrt{2}\Big[t+t^2\Big]_0^{\pi} \\[4pt] &=2\sqrt{2}(\pi+{\pi}^2). \end{align*}\]

Зверніть увагу, що це узгоджується з відповіддю в попередньому прикладі. Зміна параметризації не змінила значення лінійного інтеграла. Скалярні лінійні інтеграли не залежать від параметризації, якщо крива проходить рівно один раз параметризацією.

Вправа\(\PageIndex{3}\)

Оцініть лінійний інтеграл\(\displaystyle \int_C(x^2+yz) \,ds\), де\(C\) знаходиться лінія з параметризацією\(\vecs r(t)=⟨2t,5t,−t⟩\),\(0≤t≤10\). Перепараметризуйте С з параметризацією\(s(t)=⟨4t,10t,−2t⟩\)\(0≤t≤5\), перерахуйте лінійний інтеграл\(\displaystyle \int_C(x^2+yz) \,ds\), і зверніть увагу, що зміна параметризації не вплинула на значення інтеграла.

Підказка

Використовуйте рівняння\ ref {eq12a}.

Відповідь

Обидва лінійні інтеграли рівні\(−\dfrac{1000\sqrt{30}}{3}\).

Тепер, коли ми можемо оцінити лінійні інтеграли, ми можемо використовувати їх для обчислення довжини дуги. Якщо\(f(x,y,z)=1\), то

\[\begin{align*} \int_C f(x,y,z) \,ds &=\lim_{n\to\infty} \sum_{i=1}^{n} f(t_{i}^{*}) \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \sum_{i=1}^{n} \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \text{length} (C)\\[4pt] &=\text{length} (C). \end{align*}\]

Отже,\(\displaystyle \int_C 1 \,ds\) це довжина дуги\(C\).

Приклад\(\PageIndex{4}\): Calculating Arc Length

Дріт має форму, яку можна змоделювати за допомогою параметризації\(\vecs r(t)=⟨\cos t,\sin t,\frac{2}{3} t^{3/2}⟩\),\(0≤t≤4\pi\). Знайдіть довжину проводу.

Рішення

Довжина проводу задається тим\(\displaystyle \int_C 1 \,ds\), де\(C\) крива з параметризацією\(\vecs r\). Тому,

\[\begin{align*} \text{The length of the wire} &=\int_C 1 \,ds \\[4pt] &=\int_{0}^{4\pi} ||\vecs r′(t)||\,dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{(−\sin t)^2+\cos^2 t+t}dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{1+t} dt \\[4pt] &=\left.\dfrac{2{(1+t)}^{\frac{3}{2}}}{3} \right|_{0}^{4\pi} \\[4pt] &=\frac{2}{3}\left((1+4\pi)^{3/2}−1\right). \end{align*}\]

Вправа\(\PageIndex{4}\)

Знайти довжину проводу з параметризацією\(\vecs r(t)=⟨3t+1,4−2t,5+2t⟩\),\(0≤t≤4\).

Підказка

Знайти інтеграл прямої одиниці над відповідною кривою.

Відповідь

\(4\sqrt{17}\)

Векторні лінійні інтеграли

Другий тип лінійних інтегралів є векторними лінійними інтегралами, в які ми інтегруємо вздовж кривої через векторне поле. Наприклад, нехай

\[\vecs F(x,y,z)=P(x,y,z)\,\hat{\mathbf i}+Q(x,y,z)\,\hat{\mathbf j}+R(x,y,z)\,\hat{\mathbf k} \nonumber \]

бути безперервним векторним полем в\(ℝ^3\) тому, що являє собою силу на частинку, і нехай\(C\) бути гладкою кривою в\(ℝ^3\) міститься в області\(\vecs F\). Як би ми обчислили роботу, виконану\(\vecs F\) при переміщенні частинки вздовж\(C\)?

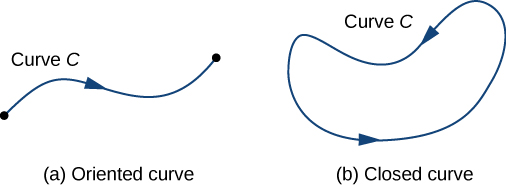
Щоб відповісти на це питання, спочатку зауважте, що частинка може рухатися у двох напрямках вздовж кривої: напрямку вперед і назад. Робота, виконана векторним полем, залежить від того, в якому напрямку рухається частка. Тому ми повинні вказати напрямок вздовж кривої\(C\); такий заданий напрямок називається орієнтацією кривої. Зазначений напрямок - позитивний напрямок вздовж\(C\); протилежний напрямок - негативний напрямок вздовж\(C\). Коли\(C\) була дана орієнтація,\(C\) називається орієнтованою кривою (рис.\(\PageIndex{5}\)). Робота, виконана над часткою, залежить від напрямку по кривій, в якому рухається частка.

Закрита крива - це та, для якої існує параметризація\(\vecs r(t)\)\(a≤t≤b\), така\(\vecs r(a)=\vecs r(b)\), що, і крива проходить рівно один раз. Іншими словами, параметризація є один-на-один на домені\((a,b)\).

Малюнок\(\PageIndex{5}\): (а) Орієнтована крива між двома точками. (б) Закрита орієнтована крива.

\(\vecs r(t)\)Дозволяти параметризації\(C\) для\(a≤t≤b\) таких, що крива проходить рівно один раз частинкою і частинка рухається в позитивному напрямку вздовж\(C\). Розділіть інтервал параметра\([a,b]\) на n підінтервалів\([t_{i−1},t_i]\)\(0≤i≤n\), однакової ширини. Позначте кінцеві точки\(r(t_0)\),\(r(t_1)\),...,\(r(t_n)\) по\(P_0\),...,\(P_n\). Точки\(P_i\)\(C\) ділимо на n частин. Позначимо довжину шматка від\(P_{i−1}\) до\(P_i\) по\(\Delta s_i\). Для кожного\(i\) виберіть значення\(t_i^*\) в підінтервалі\([t_{i−1},t_i]\). Потім кінцева точка\(\vecs r(t_i^*)\) є точкою в шматку\(C\) між\(P_{i−1}\) і\(P_i\) (рис.\(\PageIndex{6}\)). Якщо\(\Delta s_i\) невелика, то в міру руху частинки від\(P_{i−1}\) до\(P_i\) уздовж\(C\), вона рухається приблизно в напрямку\(\vecs T(P_i)\), одиниці дотичного вектора в кінцевій точці\(\vecs r(t_i^*)\). Нехай\(P_i^*\) позначають кінцеву точку\(\vecs r(t_i^*)\). Потім робота, виконана силовим векторним полем при переміщенні частинки від\(P_{i−1}\) до\(P_i\) є\(\vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))\), тому загальна робота,\(C\) виконана вздовж

\[\sum_{i=1}^n \vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))=\sum_{i=1}^n \vecs F(P_i^*)·\vecs T(P_i^*)\,\Delta s_i. \nonumber \]

Малюнок\(\PageIndex{6}\):\(C\) Крива ділиться на n частин, і вибирається точка всередині кожного шматка. Точковий добуток будь-якого дотичного вектора в i-му фрагменті з відповідним вектором\(\vecs{F}\) наближається на\(\vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\).

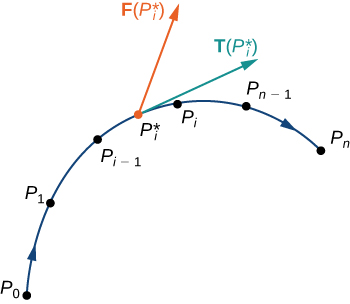
Дозволяючи довжину дуги шматочків\(C\) отримати довільно малі, приймаючи межу, як\(n\rightarrow \infty\) дає нам роботу, виконану полем у переміщенні частинки вздовж\(C\). Тому робота, виконана\(\vecs{F}\) при переміщенні частинки в позитивному напрямку уздовж\(C\), визначається як

\[W=\int_C \vecs{F} \cdot \vecs{T}\,ds, \nonumber \]

що дає нам поняття векторного інтеграла прямої.

ВИЗНАЧЕННЯ: Лінійний інтеграл векторного поля

Інтеграл векторної лінії векторного поля\(\vecs{F}\) вздовж орієнтованої гладкої кривої\(C\) дорівнює

\[\int_C \vecs{F} \cdot \vecs{T}\, ds=\lim_{n\to\infty} \sum_{i=1}^{n} \vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\Delta s_i \nonumber \]

якщо ця межа існує.

При скалярних лінійних інтегралах ні орієнтація, ні параметризація кривої не мають значення. Поки крива проходить рівно один раз параметризацією, значення лінійного інтеграла не змінюється. З векторними лінійними інтегралами орієнтація кривої має значення. Якщо ми думаємо про лінійний інтеграл як обчислювальну роботу, то це має сенс: якщо ви піднімаєтеся на гору, то гравітаційна сила Землі робить негативну роботу на вас. Якщо ви йдете по горі точно таким же шляхом, то гравітаційна сила Землі робить позитивну роботу на вас. Іншими словами, зворотний шлях змінює робоче значення з негативного на позитивне в даному випадку. Зверніть увагу, що якщо\(C\) орієнтована крива, то ми дозволяємо\(−C\) представляти ту саму криву, але з протилежною орієнтацією.

Як і у випадку зі скалярними лінійними інтегралами, простіше обчислити векторний лінійний інтеграл, якщо висловити його через функцію параметризації\(\vecs{r}\) та змінної\(t\). Щоб перевести інтеграл з\(\displaystyle \int_C \vecs{F} \cdot \vecs{T}ds\) термінами\(t\), зверніть увагу, що дотичний вектор одиниці\(\vecs{T}\) вздовж\(C\) задається\(\vecs{T}=\dfrac{\vecs{r}′(t)}{‖\vecs{r}′(t)‖}\) (припускаючи\(‖\vecs{r}′(t)‖≠0\)). Оскільки\(ds=‖\vecs r′(t)‖\,dt\), як ми бачили при обговоренні скалярних лінійних інтегралів, ми маємо

\[\vecs F·\vecs T\,ds=\vecs F(\vecs r(t))·\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}‖\vecs r′(t)‖dt=\vecs F(\vecs r(t))·\vecs r′(t)\,dt. \nonumber \]

Таким чином, ми маємо наступну формулу для обчислення векторних лінійних інтегралів:

\[\int_C\vecs F·\vecs T\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs r′(t)\,dt.\label{lineintformula} \]

Через Equation\ ref {lineintformula} ми часто використовуємо позначення\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) для лінійного інтеграла\(\displaystyle \int_C \vecs F·\vecs T\,ds\).

Якщо\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\), то\(\dfrac{d\vecs{r}}{dt}\) позначає вектор\(⟨x′(t),y′(t),z′(t)⟩\), і\(d\vecs{r} = \vecs r'(t)\,dt\).

Приклад\(\PageIndex{5}\): Evaluating a Vector Line Integral

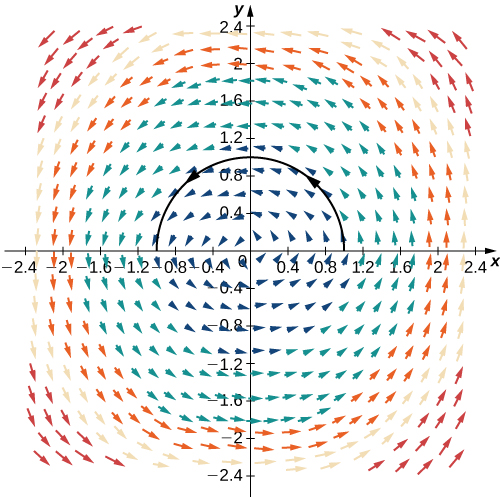
Знайти значення інтеграла\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\),\(C\) де півколо параметризується\(\vecs{r}(t)=⟨\cos t,\sin t⟩\),\(0≤t≤\pi\) і\(\vecs F=⟨−y,x⟩\).

Рішення

Ми можемо використовувати Equation\ ref {lineintformula} для перетворення змінної інтеграції з\(s\) на\(t\). У нас тоді є

\[\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩ \; \text{and} \; \vecs r′(t)=⟨−\sin t,\cos t⟩ . \nonumber \]

Тому,

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{\pi} {\sin}^2 t+{\cos}^2 t \,dt \\[4pt] &=\int_0^{\pi}1 \,dt=\pi.\end{align*}\]

Див\(\PageIndex{7}\). Малюнок.

Малюнок\(\PageIndex{7}\): На цьому малюнку показана крива\(\vecs r(t)=⟨\cos t,\,\sin t⟩\),\(0≤t≤\pi\) у векторному полі\(\vecs F=⟨−y,\,x⟩\).

Приклад\(\PageIndex{6}\): Reversing Orientation

Знайти значення інтеграла\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\),\(C\) де півколо параметризується\(\vecs r(t)=⟨\cos (t+π),\sin t⟩\),\(0≤t≤\pi\) і\(\vecs F=⟨−y,x⟩\).

Рішення

Зверніть увагу, що це та сама проблема\(\PageIndex{5}\), що і приклад, за винятком орієнтації кривої було пройдено. У цьому прикладі параметризація починається\(\vecs r(0)=⟨-1,0⟩\) і закінчується в\(\vecs r(\pi)=⟨1,0⟩\). За рівнянням\ ref {lineintformula},

\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi} ⟨−\sin t,\cos (t+\pi)⟩·⟨−\sin (t+\pi), \cos t⟩dt\\[4pt] &=\int_0^{\pi}⟨−\sin t,−\cos t⟩·⟨\sin t,\cos t⟩dt\\[4pt] &=\int_{0}^{π}(−{\sin}^2 t−{\cos}^2 t)dt \\[4pt] &=\int_{0}^{\pi}−1dt\\[4pt] &=−\pi. \end{align*}\]

Зверніть увагу, що це негативна відповідь у прикладі\(\PageIndex{5}\). Має сенс, що ця відповідь негативна, оскільки орієнтація кривої йде проти «потоку» векторного поля.

\(C\)Дозволяти орієнтована крива і нехай\(-C\) позначають ту ж криву, але з орієнтацією, зворотною. Потім два попередні приклади ілюструють наступний факт:

\[\int_{-C} \vecs{F} \cdot d\vecs{r}=−\int_C\vecs{F} \cdot d\vecs{r}. \nonumber \]

Тобто, зворотна орієнтація кривої змінює знак лінійного інтеграла.

Вправа\(\PageIndex{6}\)

\(\vecs F=x\,\hat{\mathbf i}+y \,\hat{\mathbf j}\)Дозволяти векторне поле і\(C\) нехай крива з параметризацією\(⟨t,t^2⟩\) для\(0≤t≤2\). Що більше:\(\displaystyle \int_C\vecs F·\vecs T\,ds\) або\(\displaystyle \int_{−C} \vecs F·\vecs T\,ds\)?

Підказка

Уявіть, що рухаєтеся по шляху і обчислюєте точковий продукт\(\vecs F·\vecs T\), як ви йдете.

Відповідь

\[\int_C \vecs F·\vecs T \,ds \nonumber \]

Іншим стандартним позначенням для інтеграла\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) є\(\displaystyle \int_C P\,dx+Q\,dy+R \,dz\). У цьому позначенні\(P,\, Q\), і\(R\) є функціями, і ми думаємо,\(d\vecs{r}\) як вектор\(⟨dx,dy,dz⟩\). Щоб обґрунтувати цю конвенцію, нагадайте про це\(d\vecs{r}=\vecs T\,ds=\vecs r′(t) \,dt=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Тому,

\[\vecs{F} \cdot d\vecs{r}=⟨P,Q,R⟩·⟨dx,dy,dz⟩=P\,dx+Q\,dy+R\,dz. \nonumber \]

Якщо\(d\vecs{r}=⟨dx,dy,dz⟩\), то\(\dfrac{dr}{dt}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\), що має на увазі\(d\vecs{r}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Тому

\[\begin{align} \int_C \vecs{F} \cdot d\vecs{r} &=\int_C P\,dx+Q\,dy+R\,dz \\[4pt] &=\int_a^b\left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right)\,dt. \label{eq14}\end{align} \]

Приклад\(\PageIndex{7}\): Finding the Value of an Integral of the Form \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz\)

Знайти значення інтеграла\(\displaystyle \int_C z\,dx+x\,dy+y\,dz\), де\(C\) крива параметризується\(\vecs r(t)=⟨t^2,\sqrt{t},t⟩\),\(1≤t≤4\).

Рішення

Як і в наших попередніх прикладах, для обчислення цього рядка інтеграла ми повинні виконати зміну змінних, щоб записати все з точки зору\(t\). У цьому випадку Equation\ ref {eq14} дозволяє нам зробити цю зміну:

\[\begin{align*} \int_C z\,dx+x\,dy+y\,dz &=\int_1^4 \left(t(2t)+t^2\left(\frac{1}{2\sqrt{t}}\right)+\sqrt{t}\right)\,dt \\[4pt] &=\int_1^4\left(2t^2+\frac{t^{3/2}}{2}+\sqrt{t}\right)\,dt \\[4pt] &={\left[\dfrac{2t^3}{3}+\dfrac{t^{5/2}}{5}+\dfrac{2t^{3/2}}{3} \right]}_{t=1}^{t=4} \\[4pt] &=\dfrac{793}{15}.\end{align*}\]

Вправа\(\PageIndex{7}\)

Знайти значення\(\displaystyle \int_C 4x\,dx+z\,dy+4y^2\,dz\), де\(C\) крива параметризується\(\vecs r(t)=⟨4\cos(2t),2\sin(2t),3⟩\),\(0≤t≤\dfrac{\pi}{4}\).

Підказка

Запишіть інтеграл через\(t\) використання Equation\ ref {eq14}.

Відповідь

\(−26\)

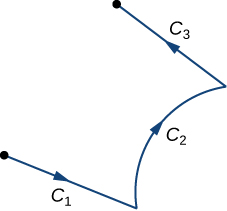
Ми навчилися інтегрувати плавні орієнтовані криві. Тепер, припустимо, що\(C\) це орієнтована крива, яка не є гладкою, але може бути записана як об'єднання скінченно багатьох плавних кривих. В даному випадку ми говоримо, що\(C\) це кусково-плавна крива. Якщо бути точним, крива\(C\) є кусково гладкою, якщо\(C\) може бути записана як об'єднання n плавних кривих\(C_1\)\(C_2\),,...,\(C_n\) таким чином, що кінцева точка\(C_i\) є початковою точкою\(C_{i+1}\) (рис.\(\PageIndex{8}\)). Коли криві\(C_i\) задовольняють умові, що кінцева точка\(C_i\) є початковою точкою\(C_{i+1}\), запишемо їх об'єднання як\(C_1+C_2+⋯+C_n\).

Малюнок\(\PageIndex{8}\): Об'єднання\(C_1\),\(C_2\),\(C_3\) являє собою кусково-гладку криву.

Наступна теорема узагальнює кілька ключових властивостей векторних лінійних інтегралів.

Теорема: Властивості векторних лінійних інтегралів

\(\vecs G\)Дозволяти\(\vecs F\) і бути неперервними векторними полями з доменами, які включають орієнтовану плавну криву\(C\). Тоді

1. \(\displaystyle \int_C(\vecs F+\vecs G)·d\vecs{r}=\int_C \vecs{F} \cdot d\vecs{r}+\int_C \vecs G·d\vecs{r}\)
2. \(\displaystyle \int_C k\vecs{F} \cdot d\vecs{r}=k\int_C \vecs{F} \cdot d\vecs{r}\), де\(k\) знаходиться постійна
3. \(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=\int_{−C}\vecs{F} \cdot d\vecs{r}\)
4. Припустимо, замість цього, що\(C\) є кусково плавна крива в областях\(\vecs F\) і\(\vecs G\), де\(C=C_1+C_2+⋯+C_n\) і\(C_1,C_2,…,C_n\) є плавними кривими таким чином, що кінцева точка\(C_i\) є початковою точкою\(C_{i+1}\). Тоді

   \[\int_C \vecs F·d\vecs{r}=\int_{C_1} \vecs F·d\vecs{r}+\int_{C_2} \vecs F·d\vecs{r}+⋯+\int_{C_n} \vecs F·d\vecs{r}. \nonumber \]

Зверніть увагу на подібність між цими елементами та властивостями однозмінних інтегралів. Властивості i. і ii. кажуть, що лінійні інтеграли лінійні, що вірно і для однозмінних інтегралів. Властивість iii. говорить про те, що зворотна орієнтація кривої змінює знак інтеграла. Якщо ми думаємо про інтеграл як обчислення роботи, виконаної над частинкою, що рухається вздовж\(C\), то це має сенс. Якщо частка рухається назад, а не вперед, то значення виконаної роботи має протилежний знак. Це аналогічно рівнянню\(\displaystyle \int_a^b f(x)\,dx=−\int_b^af(x)\,dx\). Нарешті, якщо\([a_1,a_2]\),\([a_2,a_3]\),...,\([a_{n−1},a_n]\) є інтервалами, то

\[\int_{a_1}^{a_n}f(x) \,dx=\int_{a_1}^{a_2}f(x)\,dx+\int_{a_1}^{a_3}f(x)\,dx+⋯+\int_{a_{n−1}}^{a_n} f(x)\,dx, \nonumber \]

що є аналогом властивості iv.

Приклад\(\PageIndex{8}\): Using Properties to Compute a Vector Line Integral

Знайти значення інтеграла\(\displaystyle \int_C \vecs F·\vecs T \,ds\), де\(C\) прямокутник (орієнтований проти годинникової стрілки) в площині з вершинами\((0,0)\),\((2,0)\),\((2,1)\), і\((0,1)\), і де\(\vecs F=⟨x−2y,y−x⟩\) (рис.\(\PageIndex{9}\)).

Малюнок\(\PageIndex{9}\): Прямокутник і векторне поле для Приклад\(\PageIndex{8}\).

Рішення

Зверніть увагу, що крива\(C\) - це об'єднання чотирьох її сторін, і кожна сторона гладка. Тому\(C\) буває кусково-гладкою. \(C_1\)Дозволяти представляють сторону від\((0,0)\) до\((2,0)\), нехай\(C_2\) представляють сторону від\((2,0)\) до\((2,1)\), нехай\(C_3\) представляють сторону від\((2,1)\) до\((0,1)\), і нехай\(C_4\) представляють сторону від\((0,1)\) до\((0,0)\) (Малюнок\(\PageIndex{9}\)). Потім,

\[\int_C \vecs F·\vecs T \,dr=\int_{C_1} \vecs F·\vecs T \,dr+\int_{C_2} \vecs F·\vecs T \,dr+\int_{C_3} \vecs F·\vecs T \,dr+\int_{C_4} \vecs F·\vecs T \,dr. \nonumber \]

Ми хочемо обчислити кожен з чотирьох інтегралів праворуч за допомогою Equation\ ref {eq12a}. Перш ніж це зробити, нам знадобиться параметризація кожної сторони прямокутника. Ось чотири параметризації (зверніть увагу, що вони проходять\(C\) проти годинникової стрілки):

\[\begin{align*} C_1&: ⟨t,0⟩,0≤t≤2\\[4pt] C_2&: ⟨2,t⟩, 0≤t≤1 \\[4pt] C_3&: ⟨2−t,1⟩, 0≤t≤2\\[4pt] C_4&: ⟨0,1−t⟩, 0≤t≤1. \end{align*}\]

Тому,

\[\begin{align*} \int_{C_1} \vecs F·\vecs T \,dr &=\int_0^2 \vecs F(\vecs r(t))·\vecs r′(t) \,dt \\[4pt] &=\int_0^2 ⟨t−2(0),0−t⟩·⟨1,0⟩ \,dt=\int_0^2 t \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}\Big]_0^2=2. \end{align*}\]

Зверніть увагу, що значення цього інтеграла позитивне, що не повинно дивуватися. Коли ми рухаємося по кривій\(C_1\) зліва направо, наш рух протікає в загальному напрямку самого векторного поля. У будь-якій\(C_1\) точці вздовж вектор дотичної до кривої і відповідний вектор в полі утворюють кут, який менше 90°. Отже, дотичний вектор та вектор сили мають позитивний добуток точки по всьому протязі\(C_1\), а лінійний інтеграл матиме додатне значення.

Обчислення для трьох інших лінійних інтегралів виконуються аналогічно:

\[\begin{align*} \int_{C_2} \vecs{F} \cdot d\vecs{r} &=\int_{0}^{1}⟨2−2t,t−2⟩·⟨0,1⟩ \,dt \\[4pt] &=\int_{0}^{1} (t−2) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−2t\Big]_0^1=−\dfrac{3}{2}, \end{align*}\]

\[\begin{align*} \int_{C_3} \vecs F·\vecs T \,ds &=\int_0^2⟨(2−t)−2,1−(2−t)⟩·⟨−1,0⟩ \,dt \\[4pt] &=\int_0^2t \,dt=2, \end{align*}\]

і

\[\begin{align*} \int_{C_4} \vecs{F} \cdot d\vecs{r} &=\int_0^1⟨−2(1−t),1−t⟩·⟨0,−1⟩ \,dt \\[4pt] &=\int_0^1(t−1) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−t\Big]_0^1=−\dfrac{1}{2}. \end{align*}\]

Таким чином, ми маємо\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=2\).

Вправа\(\PageIndex{8}\)

Обчислити лінійний інтеграл\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), де\(\vecs F\) знаходиться векторне поле\(⟨y^2,2xy+1⟩\) і\(C\) являє собою трикутник з вершинами\((0,0)\), і\((4,0)\)\((0,5)\), орієнтований проти годинникової стрілки.

Підказка

Запишіть трикутник як об'єднання трьох його сторін, потім обчислите три окремих лінійних інтеграла.

Відповідь

0

Застосування лінійних інтегралів

Скалярні лінійні інтеграли мають безліч застосувань. Вони можуть бути використані для розрахунку довжини або маси дроту, площі поверхні листа заданої висоти або електричного потенціалу зарядженого дроту з урахуванням лінійної щільності заряду. Векторні лінійні інтеграли надзвичайно корисні у фізиці. Вони можуть бути використані для обчислення роботи, виконаної над частинкою, коли вона рухається через силове поле, або швидкість потоку рідини по кривій. Тут обчислюємо масу дроту за допомогою скалярного лінійного інтеграла і роботу, виконану силою, використовуючи векторний лінійний інтеграл.

Припустимо, що шматок дроту моделюється кривою С в просторі. Маса на одиницю довжини (лінійна щільність) дроту є безперервною функцією\(\rho(x,y,z)\). Ми можемо обчислити загальну масу проводу за допомогою скалярного лінійного інтеграла\(\displaystyle \int_C \rho(x,y,z) \,ds\). Причина в тому, що маса - це щільність, помножена на довжину, і тому щільність невеликого шматка дроту може бути наближена\(\rho(x^*,y^*,z^*) \,\Delta s\) на якусь точку\((x^*,y^*,z^*)\) в шматку. Дозволяючи довжині шматочків скорочуватися до нуля з лімітом, виходить лінійний інтеграл\(\displaystyle \int_C \rho(x,y,z) \,ds\).

Приклад\(\PageIndex{9}\): Calculating the Mass of a Wire

Обчисліть масу пружини у формі кривої, параметризованої\(⟨t,2\cos t,2\sin t⟩\)\(0≤t≤\dfrac{\pi}{2}\), з функцією щільності, заданою\(\rho(x,y,z)=e^x+yz\) кг/м (рис.\(\PageIndex{10}\)).

Малюнок\(\PageIndex{10}\): Провід від Приклад\(\PageIndex{9}\).

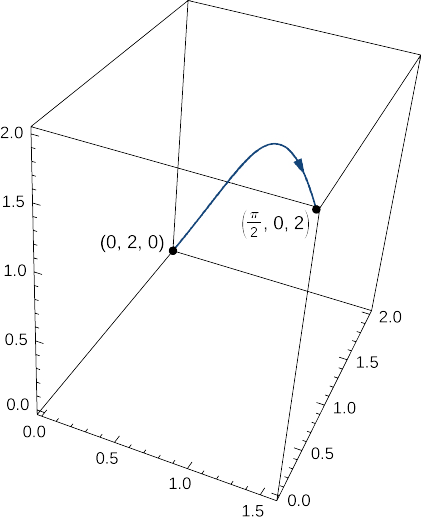
Рішення

Для обчислення маси пружини треба знайти значення скалярного лінійного інтеграла\(\displaystyle \int_C(e^x+yz)\,ds\), де\(C\) задана спіраль. Щоб обчислити цей інтеграл, запишемо його за термінами\(t\) використання Equation\ ref {eq12a}:

\[\begin{align*} \int_C \left(e^x+yz\right) \,ds &=\int_0^{\tfrac{\pi}{2}} \left((e^t+4\cos t\sin t)\sqrt{1+(−2\cos t)^2+(2\sin t)^2}\right)\,dt\\[4pt] &=\int_0^{\tfrac{\pi}{2}}\left((e^t+4\cos t\sin t)\sqrt{5}\right) \,dt \\[4pt] &=\sqrt{5}\Big[e^t+2\sin^2 t\Big]_{t=0}^{t=\pi/2}\\[4pt] &=\sqrt{5}(e^{\pi/2}+1). \end{align*}\]

Тому маса становить\(\sqrt{5}(e^{\pi/2}+1)\) кг.

Вправа\(\PageIndex{9}\)

Обчисліть масу пружини у формі спіралі, параметризованої\(\vecs r(t)=⟨\cos t,\sin t,t⟩\)\(0≤t≤6\pi\), з функцією щільності, заданою\(\rho (x,y,z)=x+y+z\) кг/м.

Підказка

Обчислити лінійний інтеграл\(\rho\) над кривою з параметризацією\(\vecs r\).

Відповідь

\(18\sqrt{2}{\pi}^2\)кг

Коли ми вперше визначили векторні лінійні інтеграли, ми використовували концепцію роботи для мотивації визначення. Тому не дивно, що обчислення роботи, виконаної векторним полем, що представляє силу, є стандартним використанням векторних лінійних інтегралів. Нагадаємо, що якщо об'єкт рухається по кривій\(C\) в\(\vecs F\) силовому полі, то робота, необхідна для переміщення об'єкта, дається\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\).

Приклад\(\PageIndex{10}\): ​​​​​​Calculating Work

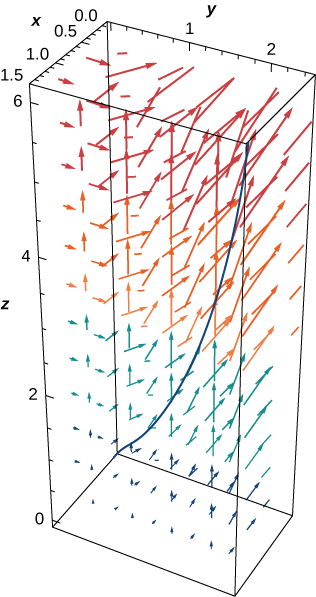
Скільки роботи потрібно для переміщення об'єкта в векторному силовому полі\(\vecs F=⟨yz,xy,xz⟩\) уздовж контуру\(\vecs r(t)=⟨t^2,t,t^4⟩,\, 0≤t≤1?\) Див\(\PageIndex{11}\). Рис.

Рішення

Нехай\(C\) позначимо заданий шлях. Нам потрібно знайти значення\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\). Для цього використовуємо рівняння\ ref {lineintformula}:

\[\begin{align*}\int_C \vecs{F} \cdot d\vecs{r} &=\int_0^1(⟨t^5,t^3,t^6⟩·⟨2t,1,4t^3⟩) \,dt \\[4pt] &=\int_0^1(2t^6+t^3+4t^9) \,dt \\[4pt] &={\Big[\dfrac{2t^7}{7}+\dfrac{t^4}{4}+\dfrac{2t^{10}}{5}\Big]}_{t=0}^{t=1}=\dfrac{131}{140}\;\text{units of work}. \end{align*}\]

Малюнок\(\PageIndex{11}\): Крива та векторне поле для Приклад\(\PageIndex{10}\).

флюс

Закриваємо цей розділ обговоренням двох ключових понять, пов'язаних з лінійними інтегралами: потік через плоску криву та циркуляцію вздовж плоської кривої. Флюс використовується в додатках для розрахунку потоку рідини через криву, а концепція циркуляції важлива для характеристики консервативних градієнтних полів з точки зору лінійних інтегралів. Обидва ці поняття широко використовуються протягом всієї іншої частини цієї глави. Ідея потоку особливо важлива для теореми Гріна, а у вищих вимірах для теореми Стокса та теореми розбіжності.

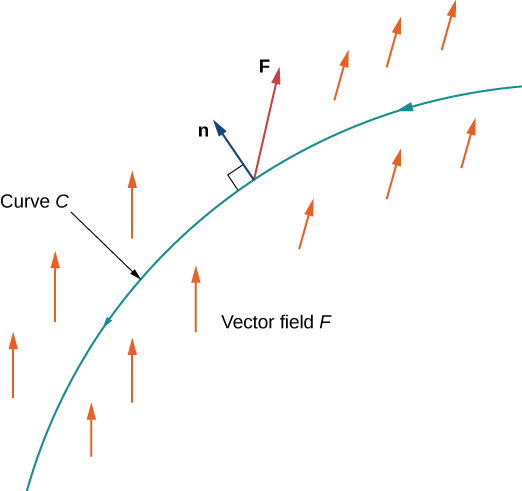
\(C\)Дозволяти площині кривої і\(\vecs F\) нехай векторне поле в площині. \(C\)Уявіть собі мембрану, по якій протікає рідина, але\(C\) не перешкоджає протіканню рідини. Іншими словами,\(C\) це ідеалізована мембрана, невидима для рідини. Припустимо,\(\vecs F\) являє собою поле швидкості рідини. Як ми можемо кількісно оцінити швидкість, з якою рідина перетинається\(C\)?

Нагадаємо, що лінійний інтеграл\(\vecs F\) вздовж\(C\) дорівнює\(\displaystyle \int_C \vecs F·\vecs T \,ds\) —іншими словами, лінійний інтеграл є точковим добутком векторного поля з одиничним тангенціальним вектором по відношенню до довжини дуги. Якщо ми замінимо одиничний тангенціальний вектор на одиничний нормальний вектор\(\vecs N(t)\) і замість цього обчислимо інтеграл\(\int_C \vecs F·\vecs N \,ds\), ми визначимо потік поперек\(C\). Якщо бути точним, то визначення інтеграла\(\displaystyle \int_C \vecs F·\vecs N \,ds\) таке ж, як і інтеграл\(\displaystyle \int_C \vecs F·\vecs T \,ds\), за винятком того, що\(\vecs T\) в сумі Рімана замінюється на\(\vecs N\). Тому потік поперек\(C\) визначається як

\[\int_C \vecs F·\vecs N \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} \vecs F(P_i^*)·\vecs N(P_i^*)\,\Delta s_i, \nonumber \]

де\(P_i^*\) і\(\Delta s_i\) визначаються, як вони були для інтегральних\(\displaystyle \int_C \vecs F·\vecs T \,ds\). Тому інтеграл потоку - це інтеграл, який перпендикулярний інтегралу векторної лінії, тому що\(\vecs N\) і\(\vecs T\) є перпендикулярними векторами.

Якщо\(\vecs F\) це поле швидкості рідини і\(C\) є кривою, яка представляє мембрану, то потік\(\vecs F\) поперек\(C\) - це кількість рідини, що протікає через\(C\) одиницю часу, або швидкість потоку.

Більш формально,\(C\) нехай плоска крива параметризується\(\vecs r(t)=⟨x(t),\,y(t)⟩\),\(a≤t≤b\). \(\vecs n(t)=⟨y′(t),\,−x′(t)⟩\)Дозволяти вектор, який є нормальним до\(C\) в кінцевій точці\(\vecs r(t)\) і вказує вправо, як ми проходимо\(C\) в позитивному напрямку (Рисунок\(\PageIndex{12}\)). Потім,\(\vecs N(t)=\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\) це одиниця нормального вектора\(C\) в кінцевій точці\(\vecs r(t)\), що вказує вправо, як ми проходимо\(C\).

ВИЗНАЧЕННЯ: Flux

Потік\(\vecs F\) поперек\(C\) є лінійним інтегралом

\[\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds. \nonumber \]

Рисунок\(\PageIndex{12}\): Потік векторного поля\(\vecs F\) по кривій\(C\) обчислюється інтегралом, подібним до векторного лінійного інтеграла.

Тепер наведемо формулу розрахунку потоку по кривій. Ця формула аналогічна формулі, яка використовується для обчислення векторного лінійного інтеграла (див. Рівняння\ ref {lineintformula}).

Теорема: Обчислення потоку по кривій

\(\vecs F\)Дозволяти векторне поле і нехай\(C\) бути плавна крива з параметризацією\(r(t)=⟨x(t),y(t)⟩\),\(a≤t≤b\) .Let\(\vecs n(t)=⟨y′(t),−x′(t)⟩\). Потік\(\vecs F\) поперек\(C\) дорівнює

\[\int_C \vecs F·\vecs N\,ds=\int_a^b\vecs F(\vecs r(t))·\vecs n(t) \,dt. \label{eq84} \]

Доказ

Перш ніж виводити формулу, зверніть увагу, що

\[‖\vecs n(t)‖=‖⟨y′(t),−x′(t)⟩‖=\sqrt{{(y′(t))}^2+{(x′(t))}^2}=‖\vecs r′(t)‖. \nonumber \]

Тому,

\[\begin{align*}\int_C \vecs F·\vecs N \,ds &=\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds \\[4pt] &=\int_a^b \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}‖\vecs r′(t)‖ \,dt \\[4pt] &=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt. \end{align*}\]

\(\square\)

Приклад\(\PageIndex{11}\): Flux across a Curve

Обчисліть потік\(\vecs F=⟨2x,2y⟩\) через одиницю окружності, орієнтованої проти годинникової стрілки (рис.\(\PageIndex{13}\)).

Малюнок\(\PageIndex{13}\): Одиничне коло у векторному полі\(\vecs F=⟨2x,\,2y⟩\).

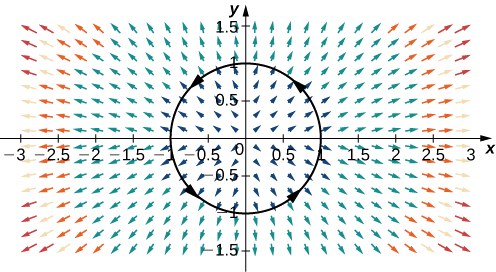
Рішення

Для обчислення потоку нам спочатку знадобиться параметризація одиничного кола. Ми можемо використовувати стандартну параметризацію\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Нормальний вектор до одиничного кола є\(⟨\cos t,\sin t⟩\). Тому флюс є

\[\begin{align*} \int_C \vecs F·\vecs N \,ds &=\int_0^{2\pi}⟨2\cos t,2\sin t⟩·⟨\cos t,\sin t⟩ \,dt\\[4pt] &=\int_0^{2\pi}(2{\cos}^2t+2{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi}({\cos}^2t+{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi} \,dt=4\pi.\end{align*}\]

Вправа\(\PageIndex{11}\)

Обчисліть потік\(\vecs F=⟨x+y,2y⟩\) по всьому відрізку лінії від\((0,0)\) до\((2,3)\), де крива орієнтована зліва направо.

Підказка

Використовуйте рівняння\ ref {eq84}.

Відповідь

\(3/2\)

\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩\)Дозволяти двовимірне векторне поле. Нагадаємо,\(\displaystyle \int_C \vecs F·\vecs T \,ds\) що інтеграл іноді пишеться як\(\displaystyle \int_C P\,dx+Q\,dy\). Аналогічно, потік\(\displaystyle \int_C \vecs F·\vecs N \,ds\) іноді записується в позначеннях\(\displaystyle \int_C −Q\,dx+P\,dy\), тому що одиничний вектор нормалі\(\vecs N\) перпендикулярний одиничному тангенсу\(\vecs T\). Обертання вектора\(d\vecs{r}=⟨dx,dy⟩\) на 90° призводить до вектора\(⟨dy,−dx⟩\). Тому лінійний інтеграл у прикладі\(\PageIndex{8}\) можна записати як\(\displaystyle \int_C −2y\,dx+2x\,dy\).

Циркуляція

Тепер, коли ми визначили потік, ми можемо звернути свою увагу на циркуляцію. Лінійний інтеграл векторного поля\(\vecs F\) по орієнтованій замкнутій кривій називається циркуляцією\(\vecs F\) вздовж\(C\). Інтеграли циркуляційної лінії мають свої позначення:\(\oint_C \vecs F·\vecs T \,ds\). Коло на інтегральному символі\(C\) позначає те, що є «круговим» тим, що воно не має кінцевих точок. \(\PageIndex{5}\)На прикладі показаний розрахунок тиражу.

Щоб побачити, звідки походить термін циркуляція і що він вимірює, нехай\(\vecs v\) представляють поле швидкості рідини і нехай\(C\) бути орієнтованою замкнутою кривою. У конкретній точці\(P\), чим ближче напрямок\(\vecs v(P)\) знаходиться до напрямку\(\vecs T(P)\), тим більше значення точкового добутку\(\vecs v(P)·\vecs T(P)\). Максимальне значення\(\vecs v(P)·\vecs T(P)\) відбувається, коли два вектори спрямовані в тому ж напрямку; мінімальне значення\(\vecs v(P)·\vecs T(P)\) відбувається, коли два вектори спрямовані в протилежні сторони. Таким чином, величина циркуляції\(\oint_C \vecs v·\vecs T \,ds\) вимірює тенденцію рідини до руху в напрямку\(C\).

Приклад\(\PageIndex{12}\): Calculating Circulation

\(\vecs F=⟨−y,\,x⟩\)Дозволяти векторне поле з Приклад\(\PageIndex{3}\) і нехай\(C\) представляють одиницю кола, орієнтовану проти годинникової стрілки. Розрахуйте циркуляцію\(\vecs F\) уздовж\(C\).

Рішення

Використовуємо стандартну параметризацію одиничного кола:\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Потім,\(\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩\) і\(\vecs r′(t)=⟨−\sin t,\cos t⟩\). Тому циркуляція\(\vecs F\) вздовж\(C\) - це

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{2\pi} ({\sin}^2 t+{\cos}^2 t) \,dt \\[4pt] &=\int_0^{2\pi} \,dt=2\pi \;\text{units of work}. \end{align*}\]

Зверніть увагу, що циркуляція позитивна. Причина цього в тому, що орієнтація\(C\) «тече» з напрямком\(\vecs F\). У будь-якій точці по колу тангенс вектор і вектор з\(\vecs F\) утворюють кут менше 90°, і тому відповідний точковий добуток є додатним.

У прикладі\(\PageIndex{12}\), що робити, якщо ми орієнтували одиницю кола за годинниковою стрілкою? Позначимо одиничне коло, орієнтоване за годинниковою стрілкою\(−C\). Тоді

\[\oint_{−C} \vecs F·\vecs T \,ds=−\oint_C \vecs F·\vecs T \,ds=−2\pi \;\text{units of work}. \nonumber \]

Зверніть увагу, що циркуляція негативна в даному випадку. Причина цього полягає в тому, що орієнтація кривої протікає проти напрямку\(\vecs F\).

Вправа\(\PageIndex{12}\)

Обчислити циркуляцію\(\vecs F(x,y)=⟨−\dfrac{y}{x^2+y^2},\,\dfrac{x}{x^2+y^2}⟩\) по одиничному колу, орієнтованому проти годинникової стрілки.

Підказка

Використовуйте рівняння\ ref {eq84}.

Відповідь

\(2\pi\)одиниць роботи

Приклад\(\PageIndex{13}\): Calculating Work

Обчисліть роботу, виконану над частинкою, яка проходить коло\(C\) радіусом 2 по центру в початковій точці, орієнтовану проти годинникової стрілки, по полю\(\vecs F(x,y)=⟨−2,\,y⟩\). Припустимо, що частка починає свій рух на\((1,\,0)\).

Рішення

Робота, виконана\(\vecs F\) на частинці, - це циркуляція\(\vecs F\) уздовж\(C\):\(\oint_C \vecs F·\vecs T \,ds\). Використовуємо параметризацію\(\vecs r(t)=⟨2\cos t,\,2\sin t⟩\),\(0≤t≤2\pi\) для\(C\). Потім,\(\vecs r′(t)=⟨−2\sin t,\,2\cos t⟩\) і\(\vecs F(\vecs r(t))=⟨−2,\,2\sin t⟩\). Тому циркуляція\(\vecs F\) вздовж\(C\) - це

\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi} ⟨−2,2\sin t⟩·⟨−2\sin t,2\cos t⟩ \,dt\\[4pt] &=\int_0^{2\pi} (4\sin t+4\sin t\cos t) \,dt\\[4pt] &={\Big[−4\cos t+4{\sin}^2 t\Big]}_0^{2\pi}\\[4pt] &=\left(−4\cos(2\pi)+2{\sin}^2(2\pi)\right)−\left(−4\cos(0)+4{\sin}^2(0)\right)\\[4pt] &=−4+4=0\;\text{units of work}.\end{align*}\]

Силове поле робить нульову роботу над частинкою.

Зверніть увагу, що циркуляція\(\vecs F\) вздовж\(C\) дорівнює нулю. Крім того, зверніть увагу, що оскільки\(\vecs F\) є градієнтом\(f(x,y)=−2x+\dfrac{y^2}{2}\),\(\vecs F\) є консервативним. У більш пізньому розділі доведено, що за певних широких умов циркуляція консервативного векторного поля по замкнутій кривій дорівнює нулю.

Вправа\(\PageIndex{14}\)

Обчисліть роботу, виконану полем\(\vecs F(x,y)=⟨2x,\,3y⟩\) на частинці, яка проходить одиничну окружність. Припустимо, що частка починає свій рух при\((−1,\,0)\).

Підказка

Використовуйте рівняння\ ref {eq84}.

Відповідь

\(0\)одиниць роботи

Ключові поняття

• Лінійні інтеграли узагальнюють поняття однозмінного інтеграла до вищих вимірів. Область інтегрування в однозмінному інтегралі - це відрізок лінії вздовж\(x\) -осі, але область інтегралу в прямому інтегралі - це крива в площині або в просторі.
• Якщо\(C\) крива, то довжина\(C\) дорівнює\(\displaystyle \int_C \,ds\).
• Існує два види лінійних інтегралів: скалярні лінійні інтеграли та векторні лінійні інтеграли. Для обчислення маси дроту можна використовувати скалярні лінійні інтеграли; векторні лінійні інтеграли можуть бути використані для обчислення роботи, виконаної над частинкою, що рухається через поле.
• Скалярні лінійні інтеграли можна обчислити за допомогою Equation\ ref {eq12a}; векторні лінійні інтеграли можна обчислити за допомогою Equation\ ref {lineintformula}.
• Двома ключовими поняттями, вираженими термінами лінійних інтегралів, є потік і циркуляція. Flux вимірює швидкість перетину поля заданої лінії; циркуляція вимірює тенденцію поля рухатися в тому ж напрямку, що і задана замкнута крива.

Ключові рівняння

• Обчислення скалярного лінійного інтеграла
  \(\displaystyle \int_C f(x,y,z) \,ds=\int_a^bf(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt\)
• Обчислення інтеграла векторної лінії
  \(\displaystyle \int_C \vecs F·d\vecs{r}=\int_C \vecs F·\vecs T \,ds=\int_a^b\vecs F(\vecs r(t))·\vecs r′(t)\,dt\)
  або
  \(\displaystyle \int_C P\,dx+Q\,dy+R\,dz=\int_a^b \left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right) \,dt\)
• Розрахунок потоку
  \(\displaystyle \int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt\)

Глосарій

циркуляції

схильність рідини рухатися у напрямку кривої\(C\). Якщо\(C\) замкнута крива, то циркуляція\(\vecs F\) уздовж\(C\) - це лінійний інтеграл\(∫_C \vecs F·\vecs T \,ds\), який ми також позначимо\(∮_C\vecs F·\vecs T \,ds\).

замкнута крива

крива, для якої існує параметризація\(\vecs r(t), a≤t≤b\), така, що\(\vecs r(a)=\vecs r(b)\), і крива проходить рівно один раз

флюс

швидкість потоку рідини через криву в векторному полі; потік векторного поля\(\vecs F\) по площині кривої\(C\) є лінійним інтегралом\(∫_C \vecs F·\frac{\vecs n(t)}{‖\vecs n(t)‖} \,ds\)

лінійний інтеграл

інтеграл функції вздовж кривої в площині або в просторі

орієнтація кривої

орієнтація кривої\(C\) - це заданий напрямок\(C\)

кусково-плавна крива

орієнтована крива, яка не є гладкою, але може бути записана як об'єднання скінченно багатьох плавних кривих

скалярний лінійний інтеграл

скалярний лінійний інтеграл функції\(f\) вздовж кривої по довжині дуги є\(C\) інтегралом\(\displaystyle \int_C f\,ds\), він є інтегралом скалярної функції\(f\) вздовж кривої в площині або в просторі; такий інтеграл визначається через суму Рімана, як однозмінний інтеграл

векторна лінія інтеграл

інтеграл векторної лінії векторного поля\(\vecs F\) вздовж кривої\(C\) є інтегралом точкового добутку\(\vecs F\) з одиничним дотичним\(\vecs T\) вектором відносно довжини дуги,\(∫_C \vecs F·\vecs T\, ds\) такий інтеграл визначається через суму Рімана, подібну до однозмінного інтеграла\(C\)