16.4: Теорема Гріна

Цілі навчання

• Застосовуємо циркуляційну форму теореми Гріна.
• Застосуйте форму флюсу теореми Гріна.
• Розрахуйте циркуляцію і потік на більш загальних регіонах.

У цьому розділі ми розглянемо теорему Гріна, яка є продовженням фундаментальної теореми числення до двох вимірів. Теорема Гріна має дві форми: форму циркуляції та форму потоку, обидві з яких вимагають простого з'єднання області$D$ в подвійному інтегралі. Однак ми поширимо теорему Гріна на регіони, які не просто пов'язані.

Простіше кажучи, теорема Гріна пов'язує лінійний інтеграл навколо просто замкнутої площини кривої$C$ та подвійний інтеграл над областю, укладеною$C$. Теорема корисна тим, що дозволяє перевести складні лінійні інтеграли в більш прості подвійні інтеграли або складні подвійні інтеграли в більш прості лінійні інтеграли.

Розширення фундаментальної теореми числення

Нагадаємо, що фундаментальна теорема обчислення говорить про те, що

$$\int_a^b F′(x)\,dx=F(b)−F(a). \nonumber$$

Як геометричний оператор, це рівняння говорить, що інтеграл над областю під графіком$F′(x)$ і вище відрізка лінії$[a,b]$ залежить тільки від значення$F$ в кінцевих точках$a$ і цього$b$ відрізка. Оскільки числа$a$ і$b$ є межею відрізка лінії, теорема говорить$[a,b]$, що ми можемо обчислити інтеграл на$\int_a^b F′(x)\,dx$ основі інформації про межі відрізка лінії$[a,b]$ (рис.$\PageIndex{1}$). Та ж ідея вірна і з фундаментальною теоремою для лінійних інтегралів:

$$\int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a)). \nonumber$$

Коли ми маємо потенційну функцію («антидериватив»), ми можемо обчислити лінійний інтеграл виключно на основі інформації про межі кривої$C$.

Малюнок$\PageIndex{1}$: Фундаментальна теорема обчислення говорить, що інтеграл над відрізком лінії$[a,b]$ залежить тільки від значень антипохідної в кінцевих точках$[a,b]$.

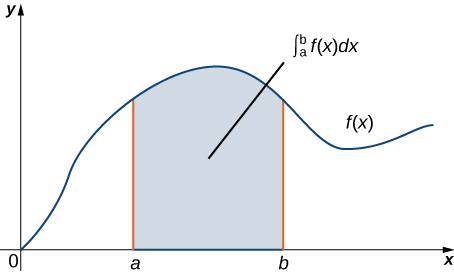
Теорема Гріна приймає цю ідею і розширює її на обчислення подвійних інтегралів. Теорема Гріна говорить, що ми можемо обчислити подвійний інтеграл над областю виключно на$D$ основі інформації про межі$D$. Теорема Гріна також говорить, що ми можемо обчислити лінійний інтеграл над простою замкнутою кривою на$C$ основі виключно інформації про область, яка$C$ охоплює. Зокрема, теорема Гріна пов'язує подвійний інтеграл над$D$ областю з лінійним інтегралом навколо межі$D$.

Форма циркуляції теореми Гріна

Перша форма теореми Гріна, яку ми вивчаємо, - це форма циркуляції. Ця форма теореми пов'язує інтеграл векторної прямої над простою, замкнутою плоской кривою$C$ з подвійним інтегралом над областю, обв'язаною$C$. Тому циркуляція векторного поля по простій замкнутій кривій може трансформуватися в подвійний інтеграл і навпаки.

ТЕОРЕМА ГРІНА (ФОРМА ЦИРКУЛЯЦІЇ)

$D$Дозволяти бути відкритою, просто пов'язаної області з граничною кривою,$C$ яка є кусково гладкою, простий замкнутої кривої, орієнтованої проти годинникової стрілки (рис.$\PageIndex{1}$). $\vecs F=⟨P,Q⟩$Дозволяти векторне поле з компонентними функціями, які мають неперервні часткові похідні на$D$. Потім,

$$\begin{align} \oint_C \vecs F·d\vecs r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align} \nonumber$$

Рисунок$\PageIndex{2}$: Форма циркуляції теореми Гріна пов'язує лінійний інтеграл над кривою$C$ з подвійним інтегралом над областю$D$.

Зверніть увагу, що теорема Гріна може бути використана тільки для двовимірного векторного поля$\vecs F$. Якщо$\vecs F$ тривимірне поле, то теорема Гріна не застосовується. Так як

$$\displaystyle \int_C P\,dx+Q\,dy=\int_C \vecs F·\vecs T\,ds \nonumber$$

цю версію теореми Гріна іноді називають тангенціальною формою теореми Гріна.

Доказ теореми Гріна є досить технічним, і виходить за рамки цього тексту. Тут ми розглянемо доказ теореми в особливому випадку, що$D$ є прямокутником. Наразі зауважте, що ми можемо швидко підтвердити, що теорема вірна для особливого випадку, в якому$\vecs F=⟨P,Q⟩$ є консервативним. У цьому випадку

$$\oint_C P\,dx+Q\,dy=0 \nonumber$$

тому що циркуляція дорівнює нулю в консервативних векторних полах. $\vecs F$задовольняє перехресне часткове умова, так$P_y=Q_x$. Тому,

$$\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy \nonumber$$

що підтверджує теорему Гріна у випадку консервативних векторних полів.

Доказ

Давайте тепер доведемо, що форма циркуляції теореми Гріна вірна, коли область$D$ є прямокутником. $D$Дозволяти прямокутник$[a,b]×[c,d]$ орієнтований проти годинникової стрілки. Потім межа$C$$D$ складається з чотирьох кусково гладких шматочків$C_1$,$C_2$,$C_3$, і$C_4$ (рис.$\PageIndex{3}$). Параметризуємо кожну сторону$D$ наступним чином:

$C_1: \vecs r_1(t)=⟨t,c⟩$,$a≤t≤b$

$C_2: \vecs r_2(t)=⟨b,t⟩$,$c≤t≤d$

$−C_3: \vecs r_3(t)=⟨t,d⟩$,$a≤t≤b$

$−C_4: \vecs r_4(t)=⟨a,t⟩$,$c≤t≤d$.

a і d > c. Сторони прямокутника - це сторона c1 з кінцевими точками в (a, c) і (b, c), сторона c2 з кінцевими точками в (b, c) і (b, d), сторона c3 з кінцевими точками в (b, d) і (a, d), і сторона c4 з кінцевими точками в (a, d) і (a, c)." style="width: 337px; height: 280px;" width="337px" height="280px" src="https://math.libretexts.org/@api/dek...065/16.4.3.png">

Малюнок$\PageIndex{3}$: Прямокутник$D$ орієнтований проти годинникової стрілки

Потім,

$$\begin{align*} \int_C \vecs F·d \vecs r &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r+\int_{C_3} \vecs F·d \vecs r+\int_{C_4} \vecs F·d \vecs r \\[4pt] &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r−\int_{−C_3} \vecs F·d \vecs r−\int_{−C_4} \vecs F·d \vecs r \\[4pt] &=\int_a^b \vecs F( \vecs r_1(t))· \vecs r_1'(t)\,dt+\int_c^d \vecs F( \vecs r_2(t))· \vecs r_2'(t)\,dt−\int_a^b \vecs F( \vecs r_3(t))· \vecs r_3'(t)\,dt−\int_c^d \vecs F( \vecs r_4(t))·\vecs r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}$$

За фундаментальною теоремою обчислення

$$P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber$$

і

$$Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber$$

Тому,

$$−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber$$

Але,

$$\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}$$

Тому$\displaystyle \int_C \vecs F\cdot d\vecs r=\iint_D(Q_x−P_y)\,dA$ і ми довели теорему Гріна у випадку прямокутника.

$\square$

Щоб довести теорему Гріна над загальною областю$D$, ми можемо$D$ розкласти на безліч крихітних прямокутників і використовувати доказ того, що теорема працює над прямокутниками. Деталі є технічними, однак, і виходять за рамки цього тексту.

Приклад$\PageIndex{1}$: Applying Green’s Theorem over a Rectangle

Обчислити лінійний інтеграл

$$\oint_C x^2ydx+(y−3)dy, \nonumber$$

де$C$ прямокутник з вершинами$(1,1)$,$(4,1)$$(4,5)$, і$(1,5)$ орієнтований проти годинникової стрілки.

Рішення

Нехай$\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩$. Потім,$Q_x(x,y)=0$ і$P_y(x,y)=x^2$. Тому,$Q_x−P_y=−x^2$.

$D$Дозволяти прямокутної області, укладеної$C$ (рис.$\PageIndex{4}$). За теоремою Гріна,

$$\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}$$

Малюнок$\PageIndex{4}$: Інтеграл прямокутника через межу прямокутника може бути перетворений у подвійний інтеграл над прямокутником.

Аналіз

Якби ми оцінили цей лінійний інтеграл без використання теореми Гріна, нам потрібно було б параметризувати кожну сторону прямокутника, розбити лінійний інтеграл на чотири окремі лінійні інтеграли та використовувати методи з розділу під назвою Лінійні інтеграли для оцінки кожного інтеграла. Крім того, оскільки векторне поле тут не є консервативним, ми не можемо застосувати фундаментальну теорему для лінійних інтегралів. Теорема Гріна значно спрощує обчислення.

Приклад$\PageIndex{2}$: Applying Green’s Theorem to Calculate Work

Обчислити виконану роботу над частинкою по силовому полю

$$\vecs F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber$$

як частинка проходить коло$x^2+y^2=4$ рівно один раз в напрямку проти годинникової стрілки, починаючи і закінчуючи в точці$(2,0)$.

Рішення

$C$Дозволяти позначити коло і нехай$D$ буде диск, укладений$C$. Робота, виконана над частинкою, є

$$W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber$$

Як і в прикладі$\PageIndex{1}$, цей інтеграл можна обчислити за допомогою вивчених нами інструментів, але простіше використовувати подвійний інтеграл, заданий теоремою Гріна (рис.$\PageIndex{5}$).

Нехай$\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩$. Потім,$Q_x=−1$ і$P_y=1$. Тому,$Q_x−P_y=−2$.

За теоремою Гріна,

$$\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}$$

Малюнок$\PageIndex{5}$: Лінійний інтеграл над граничним колом може бути перетворений у подвійний інтеграл над диском, укладеним колом.

Вправа$\PageIndex{2}$

Використовуйте теорему Гріна для обчислення лінійного інтеграла

$$\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber$$

де$C$ - прямокутний трикутник з вершинами$(−1,2)$$(4,2)$, і$(4,5)$ орієнтований проти годинникової стрілки.

Підказка

Перетворіть лінійний інтеграл в подвійний інтеграл.

Відповідь

$\dfrac{45}{2}$

У попередніх двох прикладах подвійний інтеграл в теоремі Гріна було простіше обчислити, ніж лінійний інтеграл, тому ми використовували теорему для обчислення прямої інтеграла. У наступному прикладі подвійний інтеграл обчислити складніше, ніж лінійний інтеграл, тому ми використовуємо теорему Гріна для перекладу подвійного інтеграла в прямолінійний інтеграл.

Приклад$\PageIndex{3}$: Applying Green’s Theorem over an Ellipse

Обчисліть площу, укладену еліпсом$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ (рис.$\PageIndex{6}$).

Малюнок$\PageIndex{6}$: Еліпс$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ позначається символом$C$.

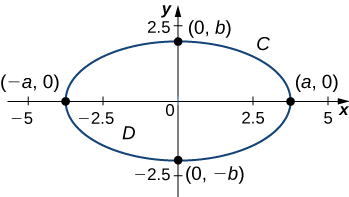
Рішення

$C$Дозволяти позначити еліпс і$D$ нехай область, укладена$C$. Нагадаємо, що еліпс$C$ можна параметризувати

• $x=a\cos t$,
• $y=b \sin t$,
• $0≤t≤2\pi$.

Обчислення площі$D$ еквівалентно обчислення подвійного інтеграла$\iint_D \,dA$. Щоб обчислити цей інтеграл без теореми Гріна, нам потрібно було б$D$ розділити на дві області: область над віссю x і область нижче. Площа еліпса дорівнює

$$\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber$$

Ці два інтеграли не просто обчислити (хоча, коли ми знаємо значення першого інтеграла, ми знаємо значення другого по симетрії). Замість того, щоб намагатися їх обчислити, ми використовуємо теорему Гріна для$\iint_D \,dA$ перетворення в лінійний інтеграл навколо кордону$C$.

Розглянемо векторне поле

$$F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber$$

Потім,$Q_x=\dfrac{1}{2}$ і$P_y=−\dfrac{1}{2}$, і тому$Q_x−P_y=1$. Зверніть увагу, що$\vecs F$ було вибрано мати властивість, що$Q_x−P_y=1$. Оскільки це так, теорема Гріна перетворює прямий інтеграл$\vecs F$ над$C$ у подвійний інтеграл 1 над$D$.

За теоремою Гріна,

$$\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \vecs F\cdot d\vecs r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}$$

Тому площа еліпса є$\pi ab\;\text{units}^2$.

У прикладі$\PageIndex{3}$ ми використовували векторне поле,$\vecs F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩$ щоб знайти площу будь-якого еліпса. Логіку попереднього прикладу можна розширити, щоб вивести формулу для площі будь-якого регіону$D$. $D$Дозволяти будь-яка область з межею, яка є простою замкнутою кривою,$C$ орієнтованою проти годинникової стрілки. Якщо$F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩$, то$Q_x−P_y=1$. Тому за тією ж логікою, що і в$\PageIndex{3}$ прикладі,

$$\text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea}$$

Варто відзначити, що якщо$F=⟨P,Q⟩$ є будь-яке векторне поле з$Q_x−P_y=1$, то працює логіка попереднього абзацу. Отже. Рівняння\ ref {greenarea} не єдине рівняння, яке використовує змішані частки векторного поля для отримання площі області.

Вправа$\PageIndex{3}$

Знайти площу області, укладеної кривою з параметризацією$r(t)=⟨\sin t\cos t,\sin t⟩$,$0≤t≤\pi$.

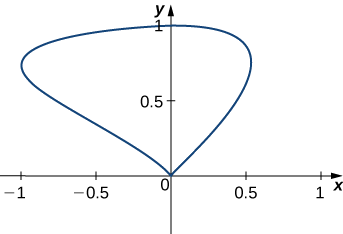
Підказка

Використовуйте рівняння\ ref {greenarea}.

Відповідь

$\dfrac{4}{3}$

Форма потоку теореми Гріна

Циркуляційна форма теореми Гріна пов'язує подвійний інтеграл над областю$D$ до лінійного інтеграла$\oint_C \vecs F·\vecs Tds$, де$C$ знаходиться межа$D$. Форма потоку теореми Гріна пов'язує подвійний інтеграл над$D$ областю до потоку через межу$C$. Потік рідини по кривій може бути важко обчислити за допомогою інтеграла лінії потоку. Така форма теореми Гріна дозволяє перевести складний інтеграл потоку в подвійний інтеграл, який часто простіше обчислити.

ТЕОРЕМА ГРІНА (ФОРМА ПОТОКУ)

$D$Дозволяти бути відкритий, просто пов'язаний область з граничної кривої,$C$ яка є кусково гладкою, простий замкнутої кривої, яка орієнтована проти годинникової стрілки (рис.$\PageIndex{7}$). $\vecs F=⟨P,Q⟩$Дозволяти векторне поле з компонентними функціями, які мають неперервні часткові похідні на відкритій області, що містять$D$. Потім,

$$\oint_C \vecs F·\vecs N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN}$$

Малюнок$\PageIndex{7}$: Форма потоку теореми Гріна пов'язує подвійний інтеграл над$D$ областю до потоку через криву$C$.

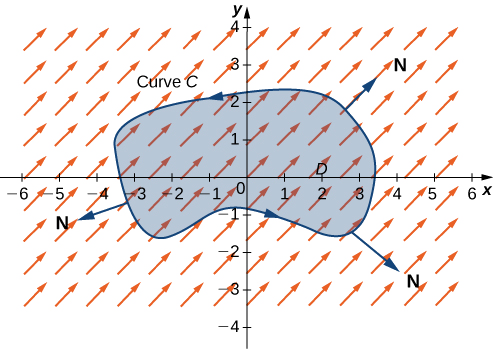
Оскільки ця форма теореми Гріна містить одиничний нормальний вектор$\vecs N$, її іноді називають нормальною формою теореми Гріна.

Доказ

Нагадаємо, що$\displaystyle \oint_C \vecs F·\vecs N\,ds=\oint_C −Q\,dx+P\,dy$. Нехай$M=−Q$ і$N=P$. За формою циркуляції теореми Гріна

$$\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}$$

$\square$

Приклад$\PageIndex{4A}$: Applying Green’s Theorem for Flux across a Circle

$C$Дозволяти бути коло радіуса по$r$ центру в початковій точці (рис.$\PageIndex{8}$) і нехай$\vecs F(x,y)=⟨x,y⟩$. Розрахуйте потік поперек$C$.

Рисунок$\PageIndex{8}$: Крива$C$ - це коло радіуса,$r$ зосереджене на початку координат.

Рішення

$D$Дозволяти бути диск, укладений$C$. Потік поперек$C$ є$\displaystyle \oint_C \vecs F·\vecs N\,ds$. Ми могли б оцінити цей інтеграл за допомогою інструментів, які ми вивчили, але теорема Гріна робить обчислення набагато простішим. Нехай$P(x,y)=x$ і$Q(x,y)=y$ так$\vecs F=⟨P,Q⟩$. Зверніть увагу$P_x=1=Q_y$, що, і тому$P_x+Q_y=2$. За теоремою Гріна,

$$\int_C \vecs F\cdot\vecs N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber$$

Так як$\displaystyle \iint_D \,dA$ це площа кола,$\displaystyle \iint_D \,dA=\pi r^2$. Тому потік поперек$C$ є$2\pi r^2$.

Приклад$\PageIndex{4B}$: Applying Green’s Theorem for Flux across a Triangle

$S$Дозволяти трикутник з вершинами$(0,0)$$(1,0)$, і$(0,3)$ орієнтований за годинниковою стрілкою (рис.$\PageIndex{9}$). Розрахуйте потік$\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩$ поперек$S$.

Рисунок$\PageIndex{9}$: Крива$S$ - це трикутник з вершинами$(0,0)$$(1,0)$,$(0,3)$ орієнтований за годинниковою стрілкою.

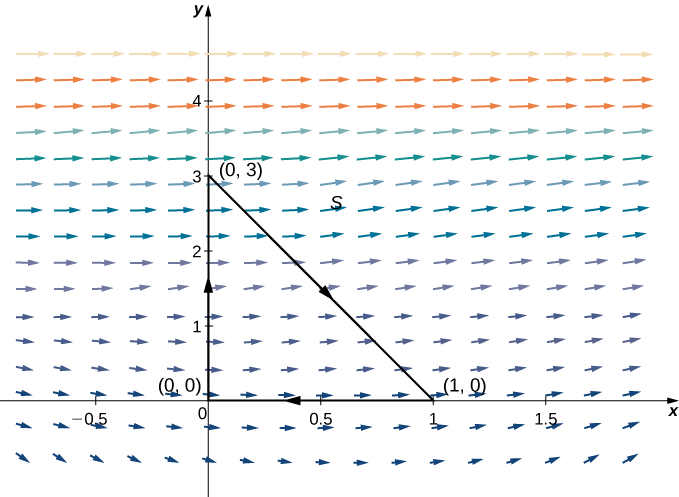
Рішення

Щоб обчислити потік без теореми Гріна, нам потрібно було б розбити інтеграл потоку на три лінійні інтеграли, по одному інтегралу для кожної сторони трикутника. Використання теореми Гріна для перекладу інтеграла прямої потоку в єдиний подвійний інтеграл набагато простіше.

$D$Дозволяти бути область, обнесена$S$. Зверніть увагу, що$P_x=2x$ і$Q_y=1$; отже,$P_x+Q_y=2x+1$. Теорема Гріна застосовується лише до простих замкнутих кривих, орієнтованих проти годинникової стрілки, але ми все ще можемо застосувати теорему, оскільки$\displaystyle \oint_C \vecs F·\vecs N\,ds=−\oint_{−S} \vecs F·\vecs N\,ds$ і$−S$ орієнтована проти годинникової стрілки. За теоремою Гріна потік

$$\begin{align*} \oint_C \vecs F·\vecs N\,ds &= \oint_{−S} \vecs F·\vecs N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}$$

Зверніть увагу, що верхній край трикутника - це лінія$y=−3x+3$. Тому в ітераційному подвійному інтегралі$y$ -значення виконуються від$y=0$ до$y=−3x+3$, і ми маємо

$$\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}$$

Вправа$\PageIndex{4}$

Обчисліть потік$\vecs F(x,y)=⟨x^3,y^3⟩$ по одиничному колу, орієнтованому проти годинникової стрілки.

Підказка

Застосуйте теорему Гріна та використовуйте полярні координати.

Відповідь

$\dfrac{3\pi}{2}$

Приклад$\PageIndex{5}$: Applying Green’s Theorem for Water Flow across a Rectangle

Вода тече з джерела, розташованого біля початку. Швидкість води моделюється векторним полем$\vecs v(x,y)=⟨5x+y,x+3y⟩$ м/сек. Знайти кількість води в секунду, яка тече через прямокутник з вершинами$(−1,−2)$,,, і$(1,−2)$$(1,3)$$(−1,3)$, орієнтована проти годинникової стрілки (рис.$\PageIndex{10}$).

Малюнок$\PageIndex{10}$: Вода тече по прямокутнику з вершинами$(−1,−2)$,,, і$(1,−2)$$(1,3)$$(−1,3)$, орієнтованими проти годинникової стрілки.

Рішення

$C$Дозволяти представляти заданий прямокутник і нехай$D$ бути прямокутної області, укладеної$C$. Щоб знайти кількість води, що протікає поперек$C$, обчислюємо потік$\int_C \vecs v\cdot d\vecs r$. Нехай$P(x,y)=5x+y$ і$Q(x,y)=x+3y$ так$\vecs v=⟨P,Q⟩$. Потім,$P_x=5$ і$Q_y=3$. За теоремою Гріна,

$$\begin{align*} \int_C \vecs v\cdot d\vecs r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}$$

Тому потік води становить 80 м ² /сек.

Нагадаємо, що якщо$\vecs F$ векторне поле консервативне, то$\vecs F$ не працює навколо замкнутих кривих - тобто циркуляція$\vecs F$ навколо замкнутої кривої дорівнює нулю. Насправді, якщо область з$\vecs F$ просто з'єднана, то консервативна тоді і тільки в$\vecs F$ тому випадку, якщо циркуляція$\vecs F$ навколо будь-якої замкнутої кривої дорівнює нулю. Якщо замінити «циркуляція$\vecs F$» на «$\vecs F$fluce of», то отримаємо визначення векторного поля без джерела. Наступні твердження є еквівалентними способами визначення поля без джерела$\vecs F=⟨P,Q⟩$ на просто пов'язаній області (зверніть увагу на схожість з властивостями консервативних векторних полів):

1. $\displaystyle \oint_C \vecs F·\vecs N\,ds$Потік по будь-якій замкнутій кривій$C$ дорівнює нулю.
2. Якщо$C_1$ і$C_2$ є кривими в області$\vecs F$ з однаковими початковими точками і кінцевими точками, то$\displaystyle \int_{C_1} \vecs F·\vecs N\,ds=\int_{C_2} \vecs F·\vecs N\,ds$. Іншими словами, флюс не залежить від шляху.
3. Є функція потоку$g(x,y)$ для$\vecs F$. Функція потоку для$\vecs F=⟨P,Q⟩$ - це функція g така, що$P=g_y$$Q=−g_x$ і.Геометрично,$\vecs F=\langle a,b\rangle$ є тангенціальною до кривої рівня$g$ at$(a,b)$. Оскільки$g$ градієнт перпендикулярний кривій рівня$g$ at$(a,b)$, функція потоку$g$ має властивість$\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0$ для будь-якої точки$(a,b)$ в області$g$. (Потокові функції відіграють ту саму роль для полів без джерел, що потенційні функції відіграють для консервативних полів.)
4. $P_x+Q_y=0$

Приклад$\PageIndex{6}$: Finding a Stream Function

Переконайтеся, що поле вектора обертання$\vecs F(x,y)=⟨y,−x⟩$ не є джерелом, і знайдіть функцію потоку для$\vecs F$.

Рішення

Зверніть увагу, що домен$\vecs F$ - це все$ℝ^2$, яке просто підключено. Тому, щоб показати,$\vecs F$ що джерело вільний, ми можемо показати будь-який з пунктів 1 по 4 з попереднього списку, щоб бути правдою. У цьому прикладі ми показуємо, що пункт 4 є істинним. Нехай$P(x,y)=y$ і$Q(x,y)=−x$. Тоді$P_x+0=Q_y$, і тому$P_x+Q_y=0$. Таким чином$\vecs F$, джерело вільний.

Щоб знайти функцію потоку для$\vecs F$, дійте так само, як і пошук потенційної функції для консервативного поля. $g$Дозволяти бути функція потоку для$\vecs F$. Потім$g_y=y$, що означає, що

$g(x,y)=\dfrac{y^2}{2}+h(x)$.

З тих пір$−g_x=Q=−x$, у нас є$h′(x)=x$. Тому,

$h(x)=\dfrac{x^2}{2}+C$.

Дозволяючи$C=0$ дає функцію потоку

$g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}$.

Щоб підтвердити, що$g$ це функція потоку для$\vecs F$, зверніть увагу, що$g_y=y=P$ і$−g_x=−x=Q$.

Зверніть увагу, що векторне поле обертання без джерела$\vecs F(x,y)=⟨y,−x⟩$ перпендикулярно консервативному радіальному векторному полю$\vecs \nabla g=⟨x,y⟩$ (рис.$\PageIndex{11}$).

а другий позначений для градієнта, дельта g = <x,>." style="width: 708px; height: 311px;" width="708px" height="311px" src="https://math.libretexts.org/@api/dek.../something.png">

Малюнок$\PageIndex{11}$: (а) На цьому зображенні ми бачимо трирівневі криві$g$ та векторного поля$\vecs F$. Зверніть увагу, що$\vecs F$ вектори на заданій кривій рівня дотичні до кривої рівня. (б) На цьому зображенні ми бачимо трирівневі криві$g$ та векторного поля$\vecs\nabla g$. Вектори градієнта перпендикулярні відповідній кривій рівня. Тому$\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0$ для будь-якої точки в області$g$.

Вправа$\PageIndex{6}$

Знайти функцію потоку для векторного поля$\vecs F(x,y)=⟨x \sin y,\cos y⟩$.

Підказка

Дотримуйтесь начерків, наведених у попередньому прикладі.

Відповідь

$g(x,y)=−x\cos y$

Векторні поля, які є консервативними та вільними джерелами, є важливими векторними полями. Однією з важливих особливостей консервативних і вільних від джерела векторних полів на просто пов'язаній області є те, що будь-яка потенційна функція$f$ такого поля задовольняє рівнянню Лапласа$f_{xx}+f_{yy}=0$. Рівняння Лапласа є основоположним у галузі рівнянь з частинними похідними, оскільки воно моделює такі явища, як гравітаційний та магнітний потенціали у просторі та потенціал швидкості ідеальної рідини. Функція, яка задовольняє рівнянню Лапласа, називається гармонічною функцією. Тому будь-яка потенційна функція консервативного і вільного від джерела векторного поля є гармонійною.

Щоб побачити, що будь-яка потенційна функція консервативного і вільного від джерела векторного поля на просто пов'язаній області є гармонічною, нехай$f$ буде така потенційна функція векторного поля$\vecs F=⟨P,Q⟩$. Потім,$f_x=P$ і$f_x=Q$ тому$\vecs \nabla f=\vecs F$. Тому$f_{xx}=P_x$ і$f_{yy}=Q_y$. Так$\vecs F$ як джерело вільний$f_{xx}+f_{yy}=P_x+Q_y=0$, і у нас є, що$f$ є гармонійним.

Приклад$\PageIndex{7}$: Satisfying Laplace’s Equation

Для векторного поля переконайтеся$\vecs F(x,y)=⟨e^x\sin y,e^x\cos y⟩$, що поле є консервативним і вільним від джерела, знайдіть потенційну функцію для та переконайтеся$\vecs F$, що потенційна функція є гармонічною.

Рішення

Нехай$P(x,y)=e^x\sin y$ і$Q(x,y)=e^x \cos y$. Зверніть увагу, що домен$\vecs F$ всього з двох просторів, який просто підключений. Тому ми можемо перевірити перехресні частки,$\vecs F$ щоб визначити, чи$\vecs F$ є консервативним. Відзначимо$P_y=e^x \cos y=Q_x$, що,$\vecs F$ так консервативно. Так як$P_x=e^x \sin y$$P_x+Q_y=0$ і$Q_y=e^x \sin y$, і поле джерело вільний.

Щоб знайти потенційну функцію для$\vecs F$, нехай$f$ буде потенційна функція. Потім$\vecs \nabla f=\vecs F$, так$f_x(x,y)=e^x \sin y$. Інтеграція цього рівняння щодо x дає$f(x,y)=e^x \sin y+h(y)$. Так як$f_y(x,y)=e^x \cos y$,$f$ диференціюючи по відношенню до y дає$e^x\cos y=e^x\cos y+h′(y)$. Тому ми можемо взяти$h(y)=0$, і$f(x,y)=e^x\sin y$ є потенційною функцією для$f$.

Щоб перевірити, що$f$ це гармонійна функція, зверніть увагу, що$f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y$ і

$f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y$. $f_{xx}+f_{yy}=0$Тому і$f$ задовольняє рівняння Лапласа.

Вправа$\PageIndex{7}$

Функція$f(x,y)=e^{x+5y}$ гармонійна?

Підказка

Визначте, чи задовольняє функція рівнянню Лапласа.

Відповідь

Ні

Теорема Гріна про загальні регіони

Теорема Гріна, як зазначено, застосовується лише до регіонів, які просто пов'язані - тобто теорема Гріна, як зазначено до цього часу, не може обробляти регіони з отворами. Тут ми розширюємо теорему Гріна так, щоб вона працювала над регіонами з скінченно великою кількістю отворів (рис.$\PageIndex{12}$).

Малюнок$\PageIndex{12}$: Теорема Гріна, як зазначено, не застосовується до непросто пов'язаної області з трьома отворами, подібними до цього.

Перш ніж обговорювати розширення теореми Гріна, нам потрібно перейти до деякої термінології щодо кордону регіону. $D$Дозволяти бути область і нехай$C$ бути складовою межі$D$. Ми говоримо,$C$ що позитивно орієнтований, якщо, коли ми йдемо$C$ в напрямку орієнтації, регіон завжди$D$ знаходиться зліва від нас. Тому орієнтація кордону диска проти годинникової стрілки є позитивною орієнтацією, наприклад. Крива$C$ негативно орієнтована, якщо, коли ми йдемо$C$ в напрямку орієнтації, область завжди$D$ знаходиться праворуч від нас. Наприклад, орієнтація кордону диска за годинниковою стрілкою є негативною орієнтацією.

$D$Дозволяти область з скінченно багато отворів (так що$D$ має скінченно багато граничних кривих), і позначити межу$D$ по$\partial D$ (Рисунок$\PageIndex{13}$). Щоб розширити теорему Гріна, щоб вона могла обробляти$D$, ми ділимо область на$D$ дві області,$D_1$ і$D_2$ (з відповідними межами$\partial D_1$ і$\partial D_2$), таким чином, що$D=D_1\cup D_2$ і ні$D_1$ ні не$D_2$ має ніяких отворів (рис.$\PageIndex{13}$).

Рисунок$\PageIndex{13}$: (a) Область$D$ з орієнтованою межею має три отвори. (b) Регіон,$D$ розділений на дві просто з'єднані області, не має отворів.

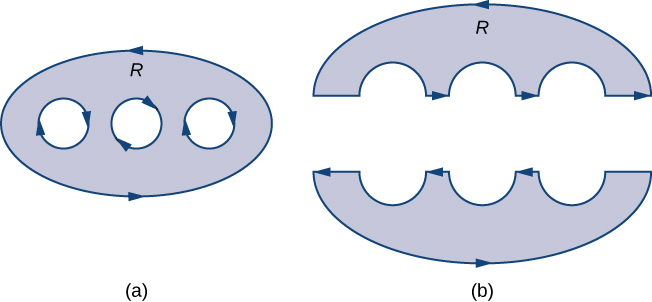
Припустимо, що межа$D$ орієнтована як на малюнку, при цьому внутрішнім отворам надається негативна орієнтація, а зовнішня межа - позитивна. Межа кожної області просто пов'язана$D_1$ і$D_2$ позитивно орієнтована. Якщо$\vecs F$ визначено векторне поле$D$, то теорема Гріна говорить, що

$$\begin{align} \oint_{\partial D} \vecs F·d\vecs{r} &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align} \nonumber$$

Тому теорема Гріна все ще працює на області з дірками.

Щоб побачити, як це працює на практиці, розглянемо кільцеве кільце на$D$ малюнку$\PageIndex{14}$ і припустимо, що$F=⟨P,Q⟩$ це векторне поле, визначене на цьому кільцевому просторі. Регіон$D$ має отвір, тому його не просто з'єднують. Орієнтуйте зовнішнє коло кільцевого кільця проти годинникової стрілки та внутрішнє коло за годинниковою стрілкою (рис.$\PageIndex{14}$), щоб$D_2$, коли ми ділимо область на$D_1$ і, ми змогли зберегти область зліва, коли ми йдемо по шляху, який проходить межу. $D_1$Дозволяти бути верхньою половиною кільцевого кільця і$D_2$ бути нижньою половиною. Жоден з цих регіонів не має дір, тому ми$D$ розділили на два просто з'єднані області.

Ми позначаємо кожен шматок цих нових меж, як$P_i$ для деяких$i$, як на малюнку$\PageIndex{14}$. Якщо ми починаємо в$P$ і подорожуємо вздовж орієнтованої межі, перший відрізок$P_1$$P_2$, потім$P_3$, і$P_4$. Тепер ми пройшли$D_1$ і повернулися до$P$. Далі починаємо$P$ знову і переходимо$D_2$. Оскільки перший шматок кордону такий же, як$P_4$ у$D_1$, але орієнтований у зворотному напрямку, перший шматок$D_2$ є$−P_4$. Далі у нас є$P_5$, потім$−P_2$, і нарешті$P_6$.

Малюнок$\PageIndex{14}$: Розрив кільцевого кільця на дві окремі області дає нам дві просто з'єднані області. Лінійні інтеграли над загальними межами скасовуються.

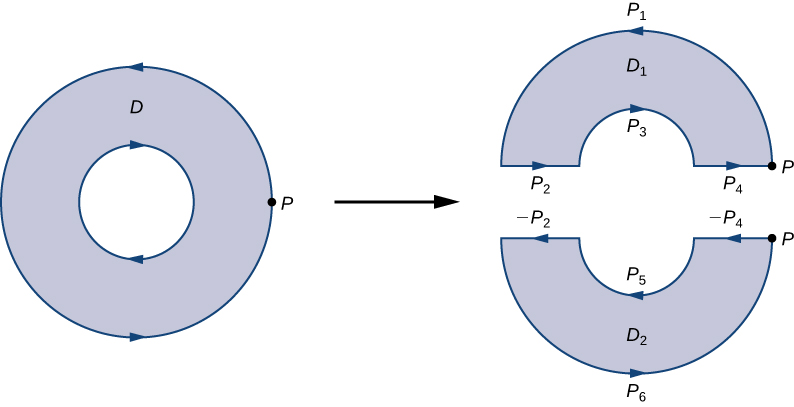
$\PageIndex{14}$На малюнку показано шлях, який проходить межу$D$. Зверніть увагу, що цей шлях проходить межу області$D_1$, повертається до початкової точки, а потім проходить межу області$D_2$. Крім того, коли ми йдемо по шляху, регіон завжди зліва від нас. Зверніть увагу, що цей обхід$P_i$ шляхів охоплює всю межу області$D$. Якби ми пройшли лише одну частину межі$D$, то ми не можемо застосувати теорему Гріна до$D$.

Межа верхньої половини кільцевого кільця, отже, є$P_1\cup P_2\cup P_3\cup P_4$ і межа нижньої половини кільцевого кільця є$−P_4\cup P_5\cup −P_2\cup P_6$. Потім теорема Гріна передбачає

$$\begin{align} \oint_{\partial D}\vecs F·d\vecs{r} &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{−P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align} \nonumber$$

Тому ми приходимо до рівняння, знайденого в теоремі Гріна, а саме:

$$\oint_{\partial D}\vecs F·d\vecs{r}=\iint_D (Q_x−P_y)\,dA. \nonumber$$

Ця ж логіка передбачає, що форма потоку теореми Гріна також може бути розширена на область з скінченно багатьма дірками:

$$\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA. \nonumber$$

Приклад$\PageIndex{8A}$: ​​​​​​Using Green’s Theorem on a Region with Holes

Обчисліть інтеграл

$$\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy, \nonumber$$

де$D$ кільцеве кільце, задане полярними нерівностями$1≤r≤2$,$0≤\theta≤2\pi$.

Рішення

Хоча$D$ це не просто пов'язано, ми можемо використовувати розширену форму теореми Гріна для обчислення інтеграла. Оскільки інтеграція відбувається над кільцевим кільцем, ми перетворюємо в полярні координати:

$$\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}$$

Приклад$\PageIndex{8B}$: Using the Extended Form of Green’s Theorem

Дозволяти$\vecs F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩$ і$C$ нехай будь-яка проста замкнута крива в площині, орієнтованої проти годинникової стрілки. Які можливі значення$\oint_C \vecs F·d\vecs{r}$?

Рішення

Ми використовуємо розширену форму теореми Гріна, щоб показати, що$\oint_C \vecs F·d\vecs{r}$ є$0$ або$−2\pi$ —тобто незалежно від того, наскільки$C$ божевільна крива, лінійний інтеграл$\vecs F$ уздовж$C$ може мати лише одне з двох можливих значень. Ми розглядаємо два випадки: випадок, коли$C$ охоплює походження і випадок, коли$C$ не охоплює походження.

Випадок 1: C не охоплює походження

У цьому випадку регіон, укладений$C$, просто з'єднаний, оскільки єдина діра в області$\vecs F$ знаходиться на початку. Ми показали в нашому обговоренні перехресні частки, які$\vecs F$ задовольняють перехресно-частковій умові. Якщо ми обмежуємо домен$\vecs F$ просто$C$ і регіон, який він охоплює, то$\vecs F$ з цим обмеженим доменом тепер визначається на просто підключений домен. Оскільки$\vecs F$ задовольняє перехресну часткову властивість на обмеженій області, поле$\vecs F$ є консервативним для цього просто пов'язаного регіону і, отже, тираж$\oint_C \vecs F·d\vecs{r}$ дорівнює нулю.

Випадок 2: C Чи охоплює походження

У цьому випадку область, обкладена не просто з'єднана, оскільки ця область містить отвір у початку.$C$ $C_1$Дозволяти бути коло радіуса a з центром на початку, так що$C_1$ повністю всередині області, укладеної$C$ (Рисунок$\PageIndex{15}$). Дайте$C_1$ орієнтацію за годинниковою стрілкою

Малюнок$\PageIndex{15}$: Виберіть коло з$C_1$ центром у початковій точці, яке повністю міститься всередині$C$.

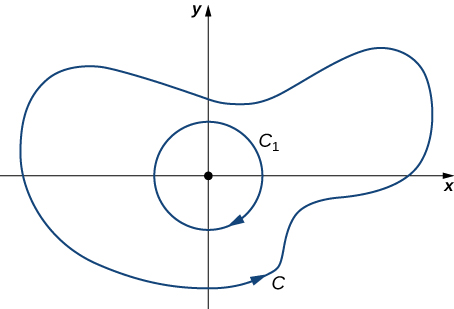
$D$Дозволяти бути область між$C_1$ і$C$, і$C$ орієнтована проти годинникової стрілки. За розширеною версією теореми Гріна

$$\begin{align*} \int_C \vecs F·d\vecs{r}+\int_{C_1}\vecs F·d\vecs{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}$$

і тому

$$\int_C \vecs F·d\vecs{r}=−\int_{C_1} \vecs F·d\vecs{r}. \nonumber$$

Так як$C_1$ є конкретна крива, ми можемо оцінити$\int_{C_1}\vecs F·d\vecs{r}$. Нехай

$$x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber$$

бути параметризацією$C_1$. Потім,

$$\begin{align*} \int_{C_1}\vecs F·d\vecs{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}$$

Тому,$\int_C F·ds=−2\pi$.

Вправа$\PageIndex{8}$

Обчисліть інтеграл$\oint_{\partial D}\vecs F·d\vecs{r}$, де$D$ знаходиться кільцеве кільце, задане полярними$0≤\theta≤2\pi$ нерівностями$2≤r≤5$, і$F(x,y)=⟨x^3,5x+e^y\sin y⟩$.

Підказка

Використовуйте розширену версію теореми Гріна.

Відповідь

$105\pi$

ВИМІРЮВАННЯ ПЛОЩІ ВІД КОРДОНУ: ПЛАНІМЕТР

Уявіть, що ви лікар, який щойно отримав магнітно-резонансне зображення мозку вашого пацієнта. Головний мозок має пухлину (рис.$\PageIndex{16}$). Наскільки велика пухлина? Якщо бути точним, то яка область червоного регіону? Червоний перетин пухлини має неправильну форму, і тому навряд чи вам вдасться знайти набір рівнянь або нерівностей для області і потім зможете обчислити її площу звичайними засобами. Ви можете наблизити площу, розрізаючи область на крихітні квадрати (підхід до суми Рімана), але цей метод завжди дає відповідь з деякою помилкою.

Малюнок$\PageIndex{16}$: Це магнітно-резонансне зображення мозку пацієнта показує пухлину, яка виділена червоним кольором. (кредит: модифікація роботи Крістара А, Wikimedia Commons)

Замість того, щоб намагатися виміряти площу області безпосередньо, ми можемо використовувати пристрій, який називається прокатним планіметром, щоб точно обчислити площу області, просто виміряючи її межу. У цьому проекті ви досліджуєте, як працює планіметр, і ви використовуєте теорему Гріна, щоб показати пристрій правильно обчислює площу.

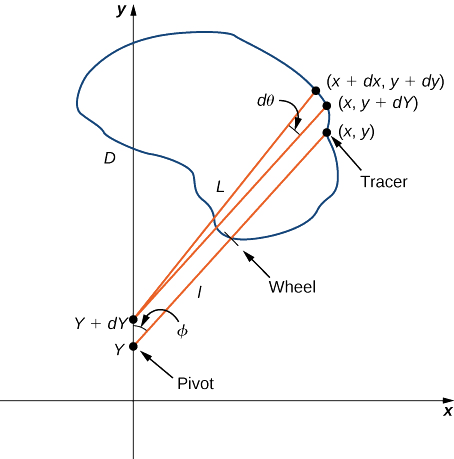
Прокатний планіметр - це пристрій, який вимірює площу площинної області, простежуючи межу цієї області (рис.$\PageIndex{17}$). Щоб виміряти площу області, ми просто запускаємо трасувальник планіметра навколо кордону області. Планіметр вимірює кількість витків, через які обертається колесо, коли ми простежуємо межу; площа форми пропорційна цій кількості обертів колеса. Ми можемо вивести точне рівняння пропорційності, використовуючи теорему Гріна. Коли трасувач рухається навколо кордону області, кронштейн трасування обертається, а ролик рухається вперед і назад (але не обертається).

Малюнок$\PageIndex{17}$: (а) прокатний планіметр. Шарнір дозволяє повороту важеля трасування. Сам ролик не обертається, він тільки рухається вперед-назад. (b) Внутрішній вигляд прокатного планіметра. Зверніть увагу, що колесо не може повертатися, якщо планувальник рухається вперед і назад з важелем трасування перпендикулярно ролику.

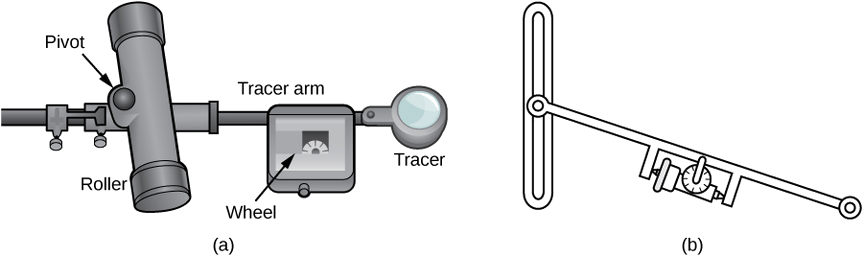
Нехай$C$ позначають межу області$D$, площа, яку потрібно обчислити. У міру проходження трасування кривої припустимо$C$, що ролик рухається по осі y (так як ролик не обертається, можна вважати, що він рухається по прямій лінії). Використовуйте$(x,y)$ координати для представлення точок на кордоні$C$, а$(0,Y)$ координати - для представлення положення повороту. Коли планіметр слідів$C$, шарнір рухається вздовж осі y, тоді як тяга трасування обертається на шарнірі.

Дивіться коротку анімацію планіметра в дії.

Почніть аналіз з розгляду руху трассера, коли він рухається від точки$(x,y)$ проти годинникової стрілки до точки$(x+dx,y+dy)$, близької до$(x,y)$ (рис.$\PageIndex{18}$). Поворот також рухається, від точки$(0,Y)$ до сусідньої точки$(0,Y+dY)$. На скільки обертається колесо в результаті цього руху? Щоб відповісти на це питання, розбийте рух на дві частини. Спочатку перекочуйте шарнір вздовж осі y від$(0,Y)$ до,$(0,Y+dY)$ не обертаючи кронштейн трасування. Потім важіль трасування закінчується в точці,$(x,y+dY)$ зберігаючи постійний кут$\phi$ з віссю x. По-друге, поверніть кронштейн трасування на кут,$d\theta$ не рухаючи ролик. Тепер трейсер знаходиться в точці$(x+dx,y+dy)$. Дозволяти буде відстань від шкворня до колеса і нехай L бути відстань від шкворня до трасера (довжина плеча трасування).

Малюнок$\PageIndex{18}$: Математичний аналіз руху планіметра.

1. Поясніть, чому загальна відстань, через яку колесо котиться тільки що описане невелике рух$\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta$.
2. Покажіть, що$\oint_C d\theta=0$.
3. Скористайтеся кроком 2, щоб показати, що загальна відстань кочення колеса, коли крива обходу трасера,$C$ є
   загальним рухом колеса$=\dfrac{1}{L}\oint_C xdY$.
   Тепер, коли у вас є рівняння для загальної відстані кочення колеса, підключіть це рівняння до теореми Гріна, щоб обчислити площу,$D$ укладену$C$.
4. Покажіть, що$x^2+(y−Y)^2=L^2$.
5. Припустимо, орієнтація планіметра така, як показано на малюнку$\PageIndex{18}$. Поясніть$Y≤y$, чому, і використовуйте цю нерівність, щоб показати, що існує унікальне значення$Y$ для кожної точки$(x,y)$:$Y=y=\sqrt{L^2−x^2}$.
6. Скористайтеся кроком 5, щоб показати, що$dY=dy+\dfrac{x}{L^2−x^2}dx.$
7. Скористайтеся теоремою Гріна, щоб показати це$\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0$.
8. Скористайтеся кроком 7, щоб показати, що загальний рулон колеса

   $$\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy. \nonumber$$

   Знадобилося трохи роботи, але це рівняння говорить про те, що змінну інтеграції Y на кроці 3 можна замінити y.

9. Використовуйте теорему Гріна, щоб показати, що площа$D$ є$\oint_C xdy$. Логіка схожа на логіку, яка використовується для того, щоб показати, що область$\displaystyle D=12\oint_C −y\,dx+x\,dy$.
10. Зробіть висновок, що площа$D$ дорівнює довжині плеча трасування, помноженої на загальну відстань кочення колеса.

Тепер ви знаєте, як працює планіметр, і ви використовували теорему Гріна, щоб обґрунтувати, що він працює. Для обчислення площі площинної області використовуйте планіметр$D$, щоб простежити межу області. Площа області - це довжина плеча трасування, помножена на відстань, яку катиться колесо.

Ключові поняття

• Теорема Гріна пов'язує інтеграл над зв'язаною областю з інтегралом над межею області. Теорема Гріна є версією фундаментальної теореми числення в одному вищому вимірі.
• Теорема Гріна поставляється в двох формах: форма циркуляції та форма потоку. У циркуляційній формі цілісний є$\vecs F·\vecs T$. У флюсовій формі цілісний є$\vecs F·\vecs N$.
• Теорема Гріна може бути використана для перетворення складного лінійного інтеграла в простіший подвійний інтеграл або для перетворення важкого подвійного інтеграла в простіший лінійний інтеграл.
• Векторне поле є джерелом вільного, якщо воно має функцію потоку. Потік векторного поля без джерела через замкнуту криву дорівнює нулю, так само як циркуляція консервативного векторного поля по замкнутій кривій дорівнює нулю.

Ключові рівняння

• Теорема Гріна
  $\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA$, форма циркуляції$C$, де межа$D$
• Теорема Гріна
  $\displaystyle ∮_C\vecs F·\vecs N\,ds=∬_D P_x+Q_y\,dA$, форма потоку$C$, де межа$D$
• Теорема Гріна, розширена версія
  $\displaystyle ∮_{\partial D}\vecs F·d\vecs{r}=∬_D Q_x−P_y\,dA$

Глосарій

Теорема Гріна

пов'язує інтеграл над зв'язаною областю до інтегралу над межею області

функція потоку

якщо$\vecs F=⟨P,Q⟩$ є джерельним векторним полем, то функція потоку$g$ - це функція така, що$P=g_y$ і$Q=−g_x$