15.7: Зміна змінних в декількох інтегралах

Цілі навчання

• Визначте зображення області при заданому перетворенні змінних.
• Обчислити якобіан заданого перетворення.
• Оцініть подвійний інтеграл за допомогою зміни змінних.
• Оцініть потрійний інтеграл за допомогою зміни змінних.

Нагадаємо з правила підстановки метод інтеграції шляхом підстановки. При оцінці інтеграла, такого як

$$\int_2^3 x(x^2 - 4)^5 dx, \nonumber$$

підставляємо$u = g(x) = x^2 - 4$. Потім$du = 2x \, dx$ або$x \, dx = \frac{1}{2} du$ і межі змінюються на$u = g(2) = 2^2 - 4 = 0$ і$u = g(3) = 9 - 4 = 5$. Таким чином, інтеграл стає

$$\int_0^5 \frac{1}{2}u^5 du \nonumber$$

і цей інтеграл набагато простіше оцінити. Іншими словами, при вирішенні інтеграційних задач ми робимо відповідні заміни, щоб отримати інтеграл, який стає набагато простішим, ніж початковий інтеграл.

Ми також використовували цю ідею, коли ми перетворювали подвійні інтеграли в прямокутні координати в полярні координати і перетворювали потрійні інтеграли в прямокутні координати в циліндричні або сферичні координати, щоб спростити обчислення. У загальному плані,

$$\int_a^b f(x) dx = \int_c^d f(g(u))g'(u) du, \nonumber$$

Де$x = g(u), \, dx = g'(u) du$,$u = c$ і$u = d$ задовольняють$c = g(a)$ і$d = g(b)$.

Аналогічний результат виникає в подвійних інтегралах, коли ми підставляємо

• $x = f (r,\theta) = r \, \cos \, \theta$
• $y = g(r, \theta) = r \, \sin \, \theta$, і
• $dA = dx \, dy = r \, dr \, d\theta$.

Тоді ми отримуємо

$$\iint_R f(x,y) dA = \iint_S (r \, \cos \, \theta, \, r \, \sin \, \theta)r \, dr \, d\theta \nonumber$$

де домен$R$ замінюється доменом$S$ у полярних координатах. Як правило, функція, яку ми використовуємо для зміни змінних, щоб спростити інтеграцію, називається перетворенням або відображенням.

Площинні перетворення

$T$Планарне перетворення - це функція, яка перетворює область$G$ в одній площині в область$R$ в іншій площині шляхом зміни змінних. Обидва$G$ і$R$ є підмножинами$R^2$. Наприклад, на малюнку$\PageIndex{1}$ показана область$G$ в$uv$ -площині перетворена$R$ в область в$xy$ -площині шляхом зміни змінних$x = g(u,v)$ і$y = h(u,v)$, або іноді ми пишемо$x = x(u,v)$ і$y = y(u,v)$. Зазвичай ми припускаємо, що кожна з цих функцій має неперервні перші часткові похідні, які означають$g_u, \, g_v, \, h_u,$ і$h_v$ існують, а також є неперервними. Необхідність цієї вимоги стане зрозумілою найближчим часом.

Малюнок$\PageIndex{1}$: Перетворення області$G$ в$uv$ -площині в область$R$ в$xy$ -площині.

Визначення: перетворення один на один

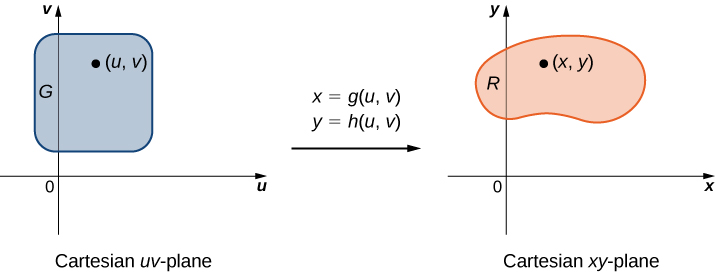
Трансформація$T: \, G \rightarrow R$, визначена як$T(u,v) = (x,y)$, вважається трансформацією один на один, якщо жодна з двох точок не відображається на одній і тій же точці зображення.

Щоб показати, що$T$ це перетворення один на один, ми припускаємо$T(u_1,v_1) = T(u_2, v_2)$ і показуємо, що як наслідок ми отримуємо$(u_1,v_1) = (u_2, v_2)$. Якщо перетворення$T$ є один-на-один в області$G$, то зворотне$T^{-1}$ існує з доменом$R$ таким, що$T^{-1} \circ T$ і$T \circ T^{-1}$ є функціями ідентичності.

$\PageIndex{2}$На малюнку показано відображення,$T(u,v) = (x,y)$ де$x$$u$ і$y$$v$ пов'язані з рівняннями$x = g(u,v)$ і$y = h(u,v)$. Регіон$G$ є доменом$T$ і регіон$R$ є діапазоном$T$, також відомий як зображення$G$ під трансформацією$T$.

Приклад$\PageIndex{1A}$: Determining How the Transformation Works

Припустимо$T$, перетворення визначається як$T(r,\theta) = (x,y)$ де$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$. Знайти зображення полярного прямокутника$G = \{(r,\theta) | 0 \leq r \leq 1, \, 0 \leq \theta \leq \pi/2\}$ в$r\theta$ -площині до області$R$ в$xy$ -площині. Покажіть, що$T$ це перетворення один на один в$G$ і знайти$T^{-1} (x,y)$.

Рішення

Оскільки$r$ змінюється від 0 до 1 в$r\theta$ -площині, у нас є круглий диск радіусом від 0 до 1 в$xy$ -площині. Оскільки$\theta$ варіюється від 0 до$\pi/2$ в$r\theta$ -площині, ми в кінцевому підсумку отримуємо чверть кола радіуса$1$ в першому квадранті$xy$ -площині (рис.$\PageIndex{2}$). Отже$R$, чверть кола обмежена$x^2 + y^2 = 1$ в першому квадранті.

Малюнок$\PageIndex{2}$: Прямокутник у$r\theta$ -площині відображається на чверть кола в$xy$ -площині.

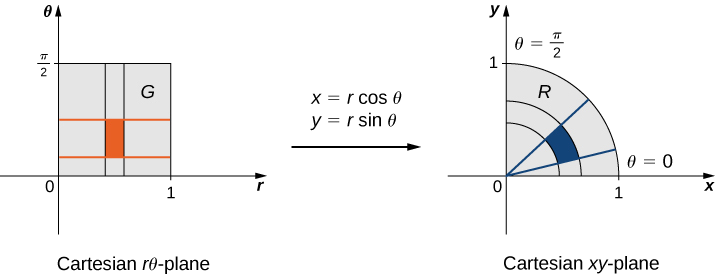
Для того, щоб показати, що$T$ це перетворення один на один, припустити$T(r_1,\theta_1) = T(r_2, \theta_2)$ і показати, як наслідок, що$(r_1,\theta_1) = (r_2, \theta_2)$. У цьому випадку ми маємо

$$T(r_1,\theta_1) = T(r_2, \theta_2), \nonumber$$

$$(x_1,y_1) = (x_1,y_1), \nonumber$$

$$(r_1 \cos \, \theta_1, r_1 \sin \, \theta_1) = (r_2 \cos \, \theta_2, r_2 \sin \, \theta_2), \nonumber$$

$$r_1 \cos \, \theta_1 = r_2 \cos \, \theta_2, \, r_1 \sin \, \theta_1 = r_2 \sin \, \theta_2. \nonumber$$

Діливши, отримуємо

$$\frac{r_1 \cos \, \theta_1}{r_1 \sin \, \theta_1} = \frac{ r_2 \cos \, \theta_2}{ r_2 \sin \, \theta_2} \nonumber$$

$$\frac{\cos \, \theta_1}{\sin \, \theta_1} = \frac{\cos \, \theta_2}{\sin \, \theta_2} \nonumber$$

$$\tan \, \theta_1 = \tan \, \theta_2 \nonumber$$

$$\theta_1 = \theta_2 \nonumber$$

так як функція дотичної є однією функцією в інтервалі$0 \leq \theta \leq \pi/2$. Крім того, з тих пір$0 \leq r \leq 1$, у нас є$r_1 = r_2, \, \theta_1 = \theta_2$. Тому$(r_1,\theta_1) = (r_2, \theta_2)$ і$T$ є трансформацією один на один від$G$ до$R$.

Знайти$T^{-1}(x,y)$ рішення для з$r,\theta$ точки зору$x,y$. Ми вже знаємо, що$r^2 = x^2 + y^2$ і$\tan \, \theta = \frac{y}{x}$. Таким чином$T^{-1}(x,y) = (r,\theta)$ визначається як$r = \sqrt{x^2 + y^2}$ і$\tan^{-1} \left(\frac{y}{x}\right)$.

Приклад$\PageIndex{1B}$: Finding the Image under $T$

Нехай перетворення$T$ буде визначено$T(u,v) = (x,y)$ де$x = u^2 - v^2$ і$y = uv$. Знайти зображення трикутника в$uv$ -площині з вершинами$(0,0), \, (0,1)$, і$(1,1)$.

Рішення

Трикутник і його зображення показані на малюнку$\PageIndex{3}$. Щоб зрозуміти, як трансформуються сторони трикутника, назвіть сторону, яка з'єднується$(0,0)$ і$(0,1)$ сторона$A$, сторона, яка з'єднується$(0,0)$ і$(1,1)$ сторона$B$, і сторону, яка з'єднується$(1,1)$ і$(0,1)$ сторону$C$.

Малюнок$\PageIndex{3}$: Трикутна область в$uv$ -площині перетворюється на зображення в$xy$ -площині.

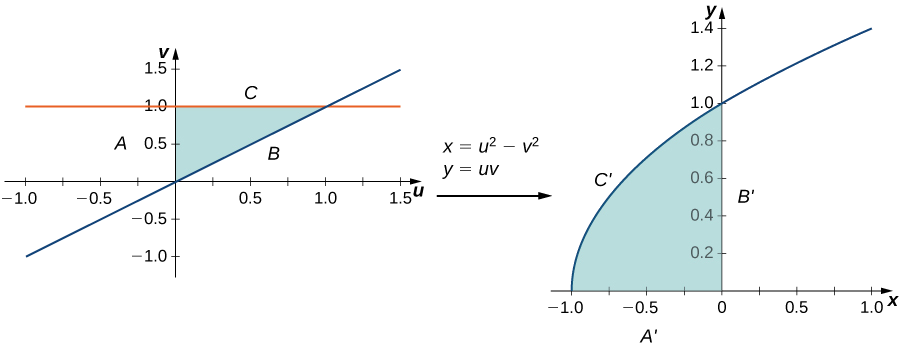
• Бо сторона$A: \, u = 0, \, 0 \leq v \leq 1$ перетворюється$x = -v^2, \, y = 0$ так це сторона,$A'$ яка приєднується$(-1,0)$ і$(0,0)$.
• Бо сторона$B: \, u = v, \, 0 \leq u \leq 1$ перетворюється$x = 0, \, y = u^2$ так це сторона,$B'$ яка приєднується$(0,0)$ і$(0,1)$.
• Бо сторона$C: \, 0 \leq u \leq 1, \, v = 1$ перетворюється в$x = u^2 - 1, \, y = u$ (отже,$x = y^2 - 1$ так це сторона$C'$, яка робить верхню половину параболічної дуги приєднання$(-1,0)$ і$(0,1)$.

Всі точки у всій області трикутника в$uv$ -площині відображені всередині параболічної області в$xy$ -площині.

Вправа$\PageIndex{1}$

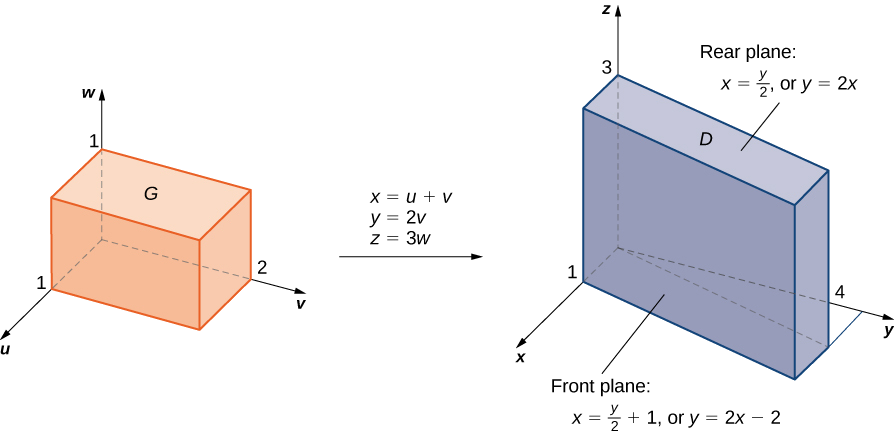
Нехай перетворення$T$ буде визначено як$T(u,v) = (x,y)$ де$x = u + v, \, y = 3v$. Знайти зображення прямокутника$G = \{(u,v) : \, 0 \leq u \leq 1, \, 0 \leq v \leq 2\}$ з$uv$ -площини після перетворення в область$R$ в$xy$ -площині. Покажіть, що$T$ це перетворення один на один і знайти$T^{-1} (x,y)$.

Підказка

Дотримуйтесь інструкцій Приклад$\PageIndex{1B}$.

Відповідь

$T^{-1} (x,y) = (u,v)$де$u = \frac{3x-y}{3}$ і$v = \frac{y}{3}$

Якобійці

Нагадаємо, що ми згадували на початку цього розділу, що кожна з компонентних функцій повинна мати неперервні перші часткові похідні, а це означає, що$g_u, g_v, h_u$ і$h_v$ існують, а також є безперервними. Трансформація, яка має цю властивість, називається$C^1$ перетворенням (тут$C$ позначається безперервне). Нехай$T(u,v) = (g(u,v), \, h(u,v))$, де$x = g(u,v)$ і$y = h(u,v)$ бути один до одного$C^1$ перетворення. Ми хочемо побачити, як він перетворює невеликі прямокутні$S, \, \Delta u$ одиниці області за$\Delta v$ одиницями, в$uv$ -площині (рис.$\PageIndex{4}$).

Малюнок$\PageIndex{4}$: Невеликий прямокутник$S$ у$uv$ -площині перетворюється на область$R$ в$xy$ -площині.

Так як$x = g(u,v)$ і$y = h(u,v)$, у нас є вектор$r(u,v) = g(u,v)i + h(u,v)j$ положення зображення точки$(u,v)$. Припустимо, що$(u_0,v_0)$ це координата точки в нижньому лівому куті, яка зіставлена$(x_0,y_0) = T(u_0,v_0)$ на Лінія$v = v_0$ відображає криву зображення з векторною функцією$r(u,v_0)$, а вектор$(x_0,y_0)$ дотичної до кривої зображення дорівнює

$$r_u = g_u (u_0,v_0)i + h_v (u_0,v_0)j = \frac{\partial x}{\partial u}i + \frac{\partial y}{\partial u}j. \nonumber$$

Аналогічно, лінія$u = u_0$ відображає криву зображення з векторною функцією$r(u_0,v)$, а дотичний вектор$(x_0,y_0)$ на кривій зображення дорівнює

$$r_v = g_v (u_0,v_0)i + h_u (u_0,v_0)j = \frac{\partial x}{\partial v}i + \frac{\partial y}{\partial v}j. \nonumber$$

Тепер зауважте, що

$$r_u = \lim_{\Delta u \rightarrow 0} \frac{r (u_0 + \Delta u, v_0) - r ( u_0,v_0)}{\Delta u}\, so \, r (u_0 + \Delta u,v_0) - r(u_0,v_0) \approx \Delta u r_u. \nonumber$$

Аналогічним чином

$$r_v = \lim_{\Delta v \rightarrow 0} \frac{r (u_0,v_0 + \Delta v) - r ( u_0,v_0)}{\Delta v}\, so \, r (u_0,v_0 + \Delta v) - r(u_0,v_0) \approx \Delta v r_v. \nonumber$$

Це дозволяє оцінити площу$\Delta A$ зображення,$R$ знайшовши площу паралелограма, утвореного сторонами$\Delta vr_v$ і$\Delta ur_u$. Використовуючи перехресний добуток цих двох векторів шляхом додавання k го компонента as$0$, площа$\Delta A$ зображення$R$ (див. Перехресний продукт) приблизно$|\Delta ur_u \times \Delta v r_v| = |r_u \times r_v|\Delta u \Delta v$. У детермінантній формі перехресний твір

$$r_u \times r_v = \begin{vmatrix} i & j & k \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0 \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \end{vmatrix} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} k = \left(\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right)k \nonumber$$

Так як у$|k| = 1,$ нас є

$\Delta A \approx |r_u \times r_v| \Delta u \Delta v = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) \Delta u \Delta v.$

Визначення: Якобійський

Якобійський$C^1$ перетворення$T(u,v) = (g(u,v), \, h(u,v))$ позначається$J(u,v)$ і визначається$2 \times 2$ детермінантою

$$J(u,v) = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right). \nonumber$$

Використовуючи визначення, ми маємо

$$\Delta A \approx J(u,v) \Delta u \Delta v = \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \Delta u \Delta v. \nonumber$$

Зауважимо, що якобійський часто позначається просто

$$J(u,v) = \frac{\partial (x,y)}{\partial (u,v)}. \nonumber$$

Зауважте також, що

$$\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \nonumber \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} . \nonumber$$

Звідси позначення$J(u,v) = \frac{\partial(x,y)}{\partial(u,v)}$ говорить про те, що ми можемо написати якобійську детермінанту з частками$x$ в першому рядку та$y$ частковими у другому рядку.

Приклад$\PageIndex{2A}$: Finding the Jacobian

Знайдіть якобійського перетворення, наведеного в прикладі$\PageIndex{1A}$.

Рішення

Трансформація в прикладі - це$T(r,\theta) = ( r \, \cos \, \theta, \, r \, \sin \, \theta)$ де$x = r \, \cos \, \theta$ і$y = r \, \sin \, \theta$. Таким чином, якобійський є

$$J(r, \theta) = \frac{\partial(x,y)}{\partial(r,\theta)} = \begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta} \end{vmatrix} = \begin{vmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos\theta \end{vmatrix} = r \, \cos^2\theta + r \, \sin^2\theta = r ( \cos^2\theta + \sin^2\theta) = r. \nonumber$$

Приклад$\PageIndex{2B}$: Finding the Jacobian

Знайдіть якобійського перетворення, наведеного в прикладі$\PageIndex{1B}$.

Рішення

Трансформація в прикладі - це$T(u,v) = (u^2 - v^2, uv)$ де$x = u^2 - v^2$ і$y = uv$. Таким чином, якобійський є

$$J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 2u & -2v \\ v & u \end{vmatrix} = 2u^2 + 2v^2. \nonumber$$

Вправа$\PageIndex{2}$

Знайдіть якобійського перетворення, наведеного в попередньому контрольному пункті:$T(u,v) = (u + v, 2v)$.

Підказка

Виконайте дії, описані в попередніх двох прикладах.

Відповідь

$$J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1 & 1 \nonumber \\ 0 & 2 \end{vmatrix} = 2 \nonumber$$

Зміна змінних для подвійних інтегралів

Ми вже бачили, що під зміною змінних$T(u,v) = (x,y)$ де$x = g(u,v)$ і невелика область$\Delta A$ в$xy$ -площині пов'язана з площею$y = h(u,v)$, утвореною добутком$\Delta u \Delta v$ в$uv$ -площині наближенням

$$\Delta A \approx J(u,v) \Delta u, \, \Delta v. \nonumber$$

Тепер повернемося до визначення подвійного інтеграла протягом хвилини:

$$\iint_R f(x,y)fA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A. \nonumber$$

Посилаючись на Малюнок$\PageIndex{5}$, зауважте, що ми розділили область$S$ в$uv$ -площині на маленькі підпрямокутники,$S_{ij}$ і ми дозволяємо підпрямокутники$R_{ij}$ в$xy$ -площині бути зображеннями$S_{ij}$ під перетворенням$T(u,v) = (x,y)$.

Малюнок$\PageIndex{5}$: Підпрямокутники$S_{ij}$ у$uv$ -площині перетворюються на підпрямокутники$R_{ij}$ у$xy$ -площині.

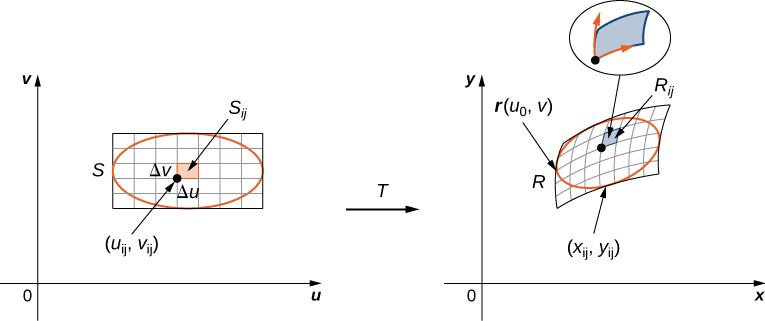
Тоді подвійний інтеграл стає

$$\iint_R = f(x,y)dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(g(u_{ij}, v_{ij}), \, h(u_{ij}, v_{ij})) | J(u_{ij}, v_{ij})| \Delta u \Delta v. \nonumber$$

Зверніть увагу, що це точно подвійна сума Рімана для інтеграла.

$$\iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber$$

Зміна змінних для подвійних інтегралів

Нехай$T(u,v) = (x,y)$ де$x = g(u,v)$ і$y = h(u,v)$ бути один до одного$C^1$ перетворення, з ненульовим якобійський на внутрішній частині області$S$ в$uv$ -площині він$S$ відображає область$R$ в$xy$ -площині. Якщо$f$ безперервно включений$R$, то

$$\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber$$

За допомогою цієї теореми для подвійних інтегралів ми можемо змінити змінні від$(x,y)$ до$(u,v)$ в подвійному інтегралі, просто замінивши

$$dA = dx \, dy = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| du \, dv \nonumber$$

коли ми використовуємо заміни,$x = g(u,v)$$y = h(u,v)$ а потім змінюємо межі інтеграції відповідно. Така зміна змінних часто робить будь-які обчислення набагато простішими.

Приклад$\PageIndex{3}$: Changing Variables from Rectangular to Polar Coordinates

Розглянемо інтегральний

$$\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx. \nonumber$$

Використовуйте зміну змінних$x = r \, \cos \, \theta$ і$y = r \, \sin \, \theta$, і знайдіть отриманий інтеграл.

Рішення

Для початку нам потрібно знайти регіон інтеграції. Ця область обмежена знизу$y = 0$ і вище по$y = \sqrt{2x - x^2}$ (рис.$\PageIndex{6}$).

Малюнок$\PageIndex{6}$: Зміна області від прямокутних до полярних координат.

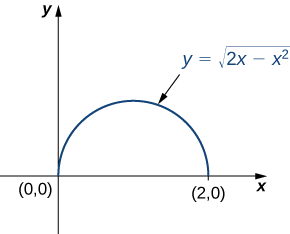
Квадратуючи і збираючи терміни, знаходимо, що область - це верхня половина кола$x^2 + y^2 - 2x = 0$, тобто$y^2 + ( x - 1)^2 = 1$. У полярних координатах коло$r = 2 \, cos \, \theta$ так область інтеграції в полярних координатах обмежена$0 \leq r \leq \cos \, \theta$ і$0 \leq \theta \leq \frac{\pi}{2}$.

Якобійський є$J(r, \theta) = r$, як показано на прикладі$\PageIndex{2A}$. З тих пір$r \geq 0$, у нас є$|J(r,\theta)| = r$.

Integrand$\sqrt{x^2 + y^2}$ змінюється на$r$ полярні координати, тому подвійний ітераційний інтеграл

$$\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r | j(r, \theta)|dr \, d\theta = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r^2 dr \, d\theta. \nonumber$$

Вправа$\PageIndex{3}$

Розглядаючи інтеграл,$\int_0^1 \int_0^{\sqrt{1-x^2}} (x^2 + y^2) dy \, dx,$ використовуйте зміну змінних$x = r \, cos \, \theta$$y = r \, sin \, \theta$ і знайдіть отриманий інтеграл.

Підказка

Виконайте дії в попередньому прикладі.

Відповідь

$$\int_0^{\pi/2} \int_0^1 r^3 dr \, d\theta \nonumber$$

Зауважте в наступному прикладі, що регіон, над яким ми маємо інтегруватися, може запропонувати відповідну трансформацію для інтеграції. Це поширена і важлива ситуація.

Приклад$\PageIndex{4}$: Changing Variables

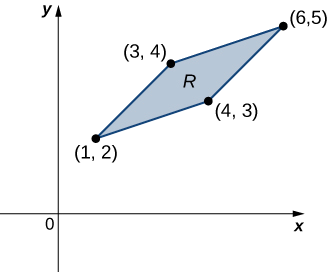
Розглянемо інтеграл $$\iint_R (x - y) dy \, dx, \nonumber$$ , де$R$ знаходиться паралелограм, що з'єднує точки$(1,2), \, (3,4), \, (4,3)$, і$(6,5)$ (рис.$\PageIndex{7}$). Внесіть відповідні зміни змінних, і запишіть отриманий інтеграл.

Малюнок$\PageIndex{7}$: Область інтеграції для даного інтеграла.

Рішення

По-перше, нам потрібно зрозуміти регіон, над яким ми маємо інтегруватися. Сторони паралелограма -$x - y + 1, \, x - y - 1 = 0, \, x - 3y + 5 = 0$ і$x - 3y + 9 = 0$ (рис.$\PageIndex{8}$). Ще один спосіб подивитися на них -$x - y = -1, \, x - y = 1, \, x - 3y = -5$ і$x - 3y = 9$.

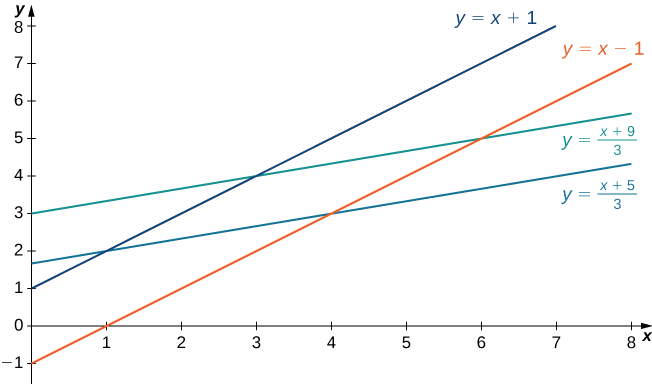
Чітко паралелограм обмежений лініями$y = x + 1, \, y = x - 1, \, y = \frac{1}{3}(x + 5)$, і$y = \frac{1}{3}(x + 9)$.

Зверніть увагу, що якби ми повинні були зробити$u = x - y$ і$v = x - 3y$, то межі на інтеграл буде$-1 \leq u \leq 1$ і$-9 \leq v \leq -5$.

Щоб вирішити для$x$ і$y$, множимо перше рівняння на$3$ і віднімаємо друге рівняння,$3u - v = (3x - 3y) - (x - 3y) = 2x$. Тоді у нас є$x = \frac{3u-v}{2}$. Причому, якщо просто відняти друге рівняння від першого, то отримаємо$u - v = (x - y) - (x - 3y) = 2y$ і$y = \frac{u-v}{2}$.

Малюнок$\PageIndex{8}$: Паралелограм у$xy$ -площині, який ми хочемо перетворити зміною змінних.

Таким чином, ми можемо вибрати трансформацію

$$T(u,v) = \left( \frac{3u - v}{2}, \, \frac{u - v}{2} \right) \nonumber$$ і обчислити якобійський$J(u,v)$. У нас є

$$J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 3/2 & -1/2 \nonumber \\ 1/2 & -1/2 \end{vmatrix} = -\frac{3}{4} + \frac{1}{4} = - \frac{1}{2} \nonumber$$

Тому,$|J(u,v)| = \frac{1}{2}$. Також оригінальним цілісним стає

$$x - y = \frac{1}{2} [3u - v - u + v] = \frac{1}{2} [3u - u] = \frac{1}{2}[2u] = u. \nonumber$$

Тому, використовуючи перетворення$T$, інтеграл змінюється на

$$\iint_R (x - y) dy \, dx = \int_{-9}^{-5} \int_{-1}^1 J (u,v) u \, du \, dv = \int_{-9}^{-5} \int_{-1}^1\left(\frac{1}{2}\right) u \, du \, dv, \nonumber$$ який набагато простіше обчислити.

Вправа$\PageIndex{4}$

Внесіть відповідні зміни змінних в інтегралі, $$\iint_R \frac{4}{(x - y)^2} dy \, dx, \nonumber$$ де$R$ трапеція обмежена лініями$x - y = 2, \, x - y = 4, \, x = 0$, і$y = 0$. Запишіть отриманий інтеграл.

Підказка

Виконайте дії в попередньому прикладі.

Відповідь

$x = \frac{1}{2}(v + u)$і$y = \frac{1}{2} (v - u)$

і

$$\int_{2}^4 \int_{-u}^u \left(\frac{1}{2}\right)\cdot\frac{4}{u^2} \,dv \, du. \nonumber$$

Ми готові дати стратегію вирішення проблем зміни змінних.

Стратегія вирішення проблем: зміна змінних

1. Намалюйте область, задану задачею в$xy$ -площині, а потім запишіть рівняння кривих, що утворюють межу.
2. Залежно від регіону або цілісності вибирають перетворення$x = g(u,v)$ і$y = h(u,v)$.
3. Визначте нові межі інтеграції в$uv$ -площині.
4. Знайдіть якобійців$J (u,v)$.
5. У integrand замініть змінні, щоб отримати новий integrand.
6. Замінити$dy \, dx$ або$dx \, dy$, в залежності від того, що відбувається, на$J(u,v) du \, dv$.

У наступному прикладі ми знаходимо підстановку, яка значно спрощує обчислення integrand.

Приклад$\PageIndex{5}$: Evaluating an Integral

Використовуючи зміну змінних$u = x - y$ і$v = x + y$, оцініть інтеграл, $$\iint_R (x - y)e^{x^2-y^2} dA, \nonumber$$ де$R$ знаходиться область, обмежена лініями$x + y = 1$$x + y = 3$ і кривими$x^2 - y^2 = -1$ і$x^2 - y^2 = 1$ (див. Перший регіон на малюнку$\PageIndex{9}$).

Рішення

Як і раніше, спочатку знайдіть область$R$ і зобразіть перетворення, щоб стало легше отримати межі інтеграції після перетворення (Рисунок$\PageIndex{9}$).

Малюнок$\PageIndex{9}$: Перетворення області$R$ в область$S$ для спрощення обчислення інтеграла.

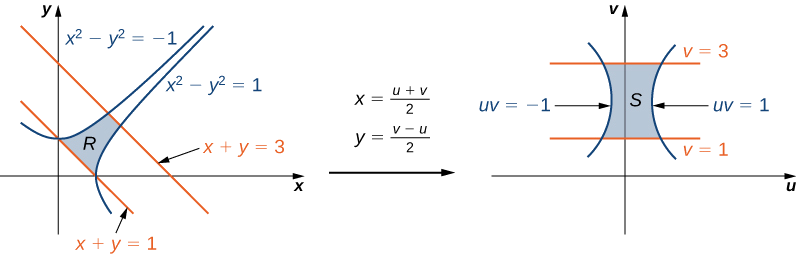
З огляду на$u = x - y$ і$v = x + y$, у нас є$x = \frac{u+v}{2}$$y = \frac{v-u}{2}$ і, отже, перетворення для використання є$T(u,v) = \left(\frac{u+v}{2}, \, \frac{v-u}{2}\right)$. Лінії$x + y = 1$ і$x + y = 3$ стають$v = 1$ і$v = 3$, відповідно. Криві$x^2 - y^2 = 1$ і$x^2 - y^2 = -1$ стають$uv = 1$ і$uv = -1$, відповідно.

Таким чином, ми можемо описати регіон$S$ (див. Рис. Другий регіон$\PageIndex{9}$) як

$$S = \left\{ (u,v) | 1 \leq v \leq 3, \, \frac{-1}{v} \leq u \leq \frac{1}{v}\right\}. \nonumber$$

Якобійський для цього перетворення є

$$J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{vmatrix} = \frac{1}{2}. \nonumber$$

Тому, використовуючи перетворення$T$, інтеграл змінюється на

$$\iint_R (x - y)e^{x^2-y^2} dA = \frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv. \nonumber$$

Роблячи оцінку, ми маємо

$$\frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv = \frac{2}{3e} \approx 0.245. \nonumber$$

Вправа$\PageIndex{5}$

Використовуючи підстановки$x = v$ і$y = \sqrt{u + v}$, оцініть інтеграл,$\displaystyle\iint_R y \, \sin (y^2 - x) \,dA,$ де$R$ знаходиться область, обмежена лініями$y = \sqrt{x}, \, x = 2$ і$y = 0$.

Підказка

Намалюйте малюнок і знайдіть межі інтеграції.

Відповідь

$\frac{1}{2} (\sin 2 - 2)$

Зміна змінних для потрійних інтегралів

Зміна змінних в потрійних інтегралах працює точно так само. Циліндричні та сферичні підстановки координат - це особливі випадки цього методу, які ми демонструємо тут.

Припустимо, що$G$ це область в$uvw$ -space і відображається$D$ в$xyz$ -space (Рисунок$\PageIndex{10}$) шляхом$C^1$ перетворення один до одного$T(u,v,w) = (x,y,z)$ де$x = g(u,v,w), \, y = h(u,v,w)$, і$z = k(u,v,w)$.

Рисунок$\PageIndex{10}$: Регіон$G$ у$uvw$ -space, зіставлений з областю$D$ у$xyz$ -space.

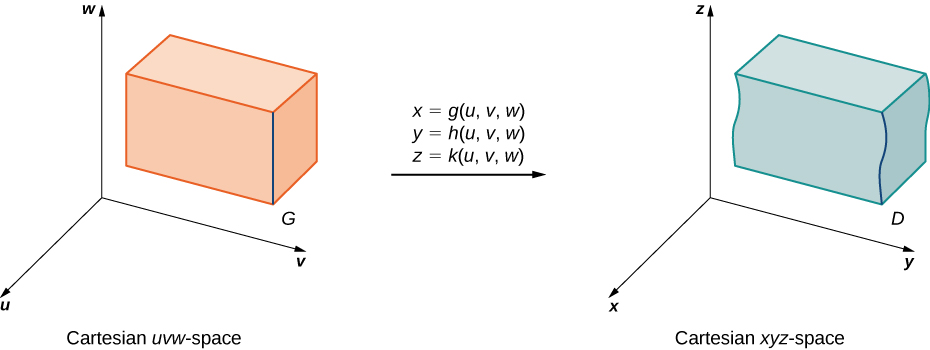
Тоді будь-яка функція,$F(x,y,z)$ визначена на,$D$ може розглядатися як інша функція$H(u,v,w)$, яка визначається на$G$:

$$F(x,y,z) = F(g(u,v,w), \, h(u,v,w), \, k(u,v,w)) = H (u,v,w). \nonumber$$

Тепер нам потрібно визначити якобіан для трьох змінних.

Визначення: Якобійська детермінанта

Якобійський детермінант$J(u,v,w)$ у трьох змінних визначається наступним чином:

$$J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} & \dfrac{\partial z}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} & \dfrac{\partial z}{\partial v} \\ \dfrac{\partial x}{\partial w} & \dfrac{\partial y}{\partial w} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber$$

Це також те ж саме, що

$$J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber$$

Якобійський також можна просто позначити як$\frac{\partial(x,y,z)}{\partial (u,v,w)}$.

З перетвореннями і якобійським для трьох змінних ми готові встановити теорему, яка описує зміну змінних для потрійних інтегралів.

Зміна змінних для потрійних інтегралів

Нехай$T(u,v,w) = (x,y,z)$ де$x = g(u,v,w), \, y = h(u,v,w)$, і$z = k(u,v,w)$, бути один до одного$C^1$ перетворення, з ненульовим якобіан, що відображає область$G$ в$uvw$ -space в область$D$ в$xyz$ -space. Як і в двомірному випадку,$F$ якщо безперервне включення$D$, то

$$\begin{align} \iiint_D F(x,y,z) dV = \iiint_G f(g(u,v,w) \, h(u,v,w), \, k(u,v,w)) \left|\frac{\partial (x,y,z)}{\partial (u,v,w)}\right| du \, dv \, dw \\ = \iiint_G H(u,v,w) | J (u,v,w) | du \, dv \, dw. \end{align} \nonumber$$

Давайте тепер подивимося, як впливає ця теорема на зміни потрійних інтегралів для циліндричних і сферичних координат. Ми очікуємо отримати ті ж формули, що і в потрійних інтегралах в циліндричних і сферичних координатах.

Приклад$\PageIndex{6A}$: Obtaining Formulas in Triple Integrals for Cylindrical and Spherical Coordinates

Вивести формулу в потрійних інтегралах для

1. циліндричні і
2. сферичні координати.

Рішення

А.

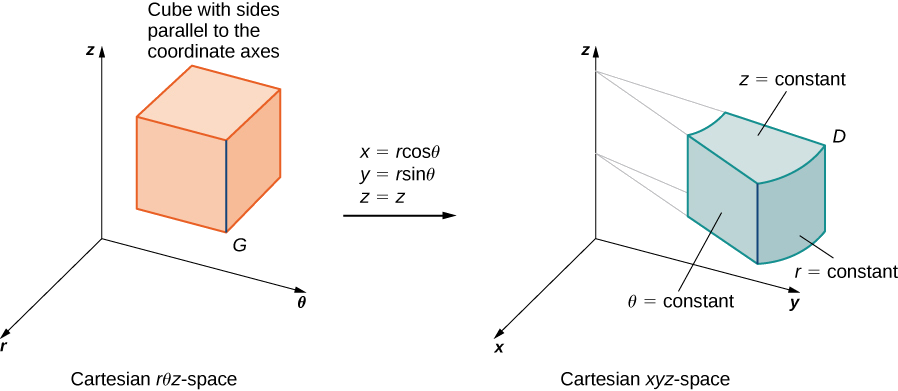
Для циліндричних координат перетворення відбувається$T (r, \theta, z) = (x,y,z)$ з$r\theta z$ декартового -простору в декартовий$xyz$ -простір (рис.$\PageIndex{11}$). Ось$x = r \, \cos \, \theta, \, y = r \, \sin \theta$ і$z = z$. Якобійський для перетворення є

$$J(r,\theta,z) = \frac{\partial (x,y,z)}{\partial (r,\theta,z)} = \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z} \end{vmatrix} \nonumber$$

$$\begin{vmatrix} \cos \theta & -r\sin \theta & 0 \\ \sin \theta & r \cos \theta & 0 \\ 0 & 0 & 1 \end{vmatrix} = r \, \cos^2 \theta + r \, \sin^2 \theta = r. \nonumber$$

Ми це знаємо$r \geq 0$, так$|J(r,\theta,z)| = r$. Тоді потрійний інтеграл дорівнює $$\iiint_D f(x,y,z)dV = \iiint_G f(r \, \cos \theta, \, r \, \sin \theta, \, z) r \, dr \, d\theta \, dz. \nonumber$$

Рисунок$\PageIndex{11}$: Перетворення від прямокутних координат до циліндричних координат може розглядатися як зміна змінних від області$G$ в$r\theta z$ -space до області$D$ в$xyz$ -space.

Б.

Для сферичних координат перетворення відбувається$T(\rho,\theta,\varphi)$ з$\rho\theta\varphi$ декартового -простору в декартовий$xyz$ -простір (рис.$\PageIndex{12}$). Ось$x = \rho \, \sin \varphi \, \cos \theta, \, y = \rho \, \sin \varphi \, \sin \theta$, і$z = \rho \, \cos \varphi$. Якобійський для перетворення є

$$J(\rho,\theta,\varphi) = \frac{\partial (x,y,z)}{\partial (\rho,\theta,\varphi)} = \begin{vmatrix} \frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \varphi} \\ \frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \varphi} \end{vmatrix} = \begin{vmatrix} \sin \varphi \cos \theta & -\rho \sin \varphi \sin \theta & \rho \cos \varphi \cos \theta \\ \sin \varphi \sin \theta & \rho \sin \varphi \cos \theta & \rho \cos \varphi \sin \theta \\ \cos \varphi & 0 & -\rho \sin \varphi \end{vmatrix}. \nonumber$$

Розширення визначника щодо третього ряду:

\ [\ почати {align*} &=\ cos\ varphi\ почати {vmatrix} -\ rho\ sin\ varphi\ sin\ тета &\ rho\ cos\ тета\\ тета\\ rho\ varphi\ cos\ sin\ theta\ end {vmatrix} -\ rho\ varphi\ {vmatrix}\ sin\ varphi\ cos\ тета & -\ rho\ sin\ varphi\ sin\ тета\\ sin\ варфі\ грін\ тета &\ rho\ sin\ varphi\ cos\ тета\ кінець {vmatrix}\\ [4pt]
&=\ cos\ varphi (-\ rho^2\ varphi\,\ cos\ varphi\,\ cos\ varphi\,\ cos\ varphi\,\ cos\ varphi\,\ cos\ varphi\,\ cos ^ 2\ theta\)\ &\ квад -\ рхо\ грін\ варфі (\ рхо\ сін^2\ варфі\ cos^2\ тета +\ рхо\ sin^2\ варфі\ sin^2\ тета)\\ [4pt]
&=-\ rho^2\ sin\ varphi\ cos^2\ varphi (\ sin^2\ тета +\ cos^2\ тета) -\ rho^2\ teta\\ theta)\\ [4pt]
&= -\ rho^2\ sin\ варфі\ cos^2\ варфі -\ rho^2\ sin\ варфі\ sin^2\ варфі\\ [4pt]
&= -\ rho \ sin\ варфі (\ cos^2\ варфі +\ sin^2\ varphi) = -\ rho^2\ sin\ varphi. \ end {вирівнювати*}\]

Так як$0 \leq \varphi \leq \pi$, ми повинні мати$\sin \varphi \geq 0$. Таким чином$|J(\rho,\theta, \varphi)| = |-\rho^2 \sin \varphi| = \rho^2 \sin \varphi.$

Рисунок$\PageIndex{12}$: Перетворення від прямокутних координат до сферичних координат може розглядатися як зміна змінних від області$G$ в$\rho\theta\varphi$ -space до області$D$ в$xyz$ -space.

Тоді потрійний інтеграл стає

$$\iiint_D f(x,y,z) dV = \iiint_G f(\rho \, \sin \varphi \, \cos \theta, \, \rho \, \sin \varphi \, \sin \theta, \rho \, \cos \varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta. \nonumber$$

Спробуємо інший приклад з іншою підміною.

Приклад$\PageIndex{6B}$: Evaluating a Triple Integral with a Change of Variables

Оцініть потрійний інтеграл

$$\int_0^3 \int_0^4 \int_{y/2}^{(y/2)+1} \left(x + \frac{z}{3}\right) dx \, dy \, dz \nonumber$$

In$xyz$ -space за допомогою перетворення

$u = (2x - y) /2, \, v = y/2$, і$w = z/3$.

Потім інтегруйте над відповідним регіоном у$uvw$ -space.

Рішення

Як і раніше, якийсь ескіз області$G$ в$xyz$ -просторі, над яким ми маємо виконати інтеграцію, може допомогти ідентифікувати область$D$ в$uvw$ -просторі (рис.$\PageIndex{13}$). Чітко$G$ в$xyz$ -просторі обмежується площинами$x = y/2, \, x = (y/2) + 1, \, y = 0, \, y = 4, \, z = 0$, і$z = 4$. Ми також знаємо, що ми повинні використовувати$u = (2x - y) /2, \, v = y/2$ і$w = z/3$ для перетворень. Нам потрібно вирішувати за$x,y$ і$z$. Тут ми знаходимо$x = u + v, \, y = 2v$, що, і$z = 3w$.

Рисунок$\PageIndex{13}$: Область$G$ в$uvw$ -просторі перетворюється на область$D$ в$xyz$ -просторі.

Використовуючи елементарну алгебру, ми можемо знайти відповідні поверхні для області$G$ та межі інтеграції в$uvw$ -просторі. Ці рівняння зручно перераховувати в таблиці.

$xyz$Рівняння в області$D$	Відповідні рівняння в$uvw$ області$G$	Обмеження для інтеграції в$uvw$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$x = y/2$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$u + v = 2v/2 = v$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$u = 0$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$x = y/2$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$u + v = (2v/2) + 1 = v + 1$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$u = 1$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$y = 0$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$2v = 0$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$v = 0$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$y = 4$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$2v = 4$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$v = 2$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$z = 0$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$3w = 0$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$w = 0$
\ (xyz\) для області$D$ "style="вертикальне вирівнювання: middle;" >$z = 3$	\ (uvw\) для області$G$ "style="вертикальне вирівнювання: middle;" >$3w = 3$	\ (uvw\)» style="вертикальне вирівнювання: середина; ">$w = 1$

Тепер ми можемо обчислити якобіан для перетворення:

$$J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix} = \begin{vmatrix} 1 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{vmatrix} = 6. \nonumber$$

Функція, яку потрібно інтегрувати, стає

$$f(x,y,z) = x + \frac{z}{3} = u + v + \frac{3w}{3} = u + v + w. \nonumber$$

Тепер ми готові зібрати все воєдино і завершити проблему.

\ [\ почати {align*}\ int_0^3\ int_0^4\ int_ {y/2} ^ {(y/2) +1}\ вліво (x +\ frac {z} {3}\ праворуч) dx\, dy\, dz &=\ int_0^1\ int_0^2\ int_0^1 (u + v + w) |J (u, v, v, w) |ду\, дв\, дв\\ [4пт]
&=\ int_0^1\ int_0^2\ int_0^1 (u + v + w) |6|ду\, дв\, дв\\ [4пт]
&= 6\ int_0^1\ int_0^2\ int_ 0^1 (u + v + w)\, ду\, дв\, дв\\ [4пт]
&= 6\ int_0^1\ int_0^2\ ліворуч [\ frac {u^2} {2} + ву\\ вправо] _0^1\, dv\, dw\\ [4pt]
&= 6\ int_0^1\ int_0^2\ ліворуч (\ розрив {1} {2} + v + u\ праворуч) dv\, dw\\ [4pt]
&= 6\ int_0^1\ ліворуч [\ розрив {1} {2} v +\ frac {v^2} {2} + wv\ праворуч] _0^2 dw\\ [4pt]
&= 6\ int_0^1 (3 + 2w)\, dw = 6\ великий [3w + w^2\ Big] _0^1 = 24. \ end {вирівнювати*}\]

Вправа$\PageIndex{6}$

$D$Дозволяти бути область в$xyz$ -space$1 \leq x \leq 2, \, 0 \leq xy \leq 2$, визначена, і$0 \leq z \leq 1$.

Оцініть$\iiint_D (x^2 y + 3xyz) \, dx \, dy \, dz$ за допомогою перетворення$u = x, \, v = xy$, і$w = 3z$.

Підказка

Складіть таблицю для кожної поверхні регіонів і визначитеся з межами, як показано на прикладі.

Відповідь

$$\int_0^3 \int_0^2 \int_1^2 \left(\frac{v}{3} + \frac{vw}{3u}\right) du \, dv \, dw = 2 + \ln 8 \nonumber$$

Ключові концепції

• Трансформація$T$ - це функція, яка перетворює область$G$ в одній площині (просторі) в$R$ область. в іншій площині (просторі) шляхом зміни змінних.
• Трансформація,$T: G \rightarrow R$ визначена як$T(u,v) = (x,y)$ (або, як кажуть,$T(u,v,w) = (x,y,z))$ є трансформацією один на один, якщо жодна дві точки не відображаються на одній і тій же точці зображення.
• Якщо$f$ безперервно включений$R$, то $$\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial(x,y)}{\partial (u,v)}\right| du \, dv. \nonumber$$
• Якщо$F$ безперервно включений$R$, то $$\begin{align*}\iiint_R F(x,y,z) \, dV &= \iiint_G F(g(u,v,w), \, h(u,v,w), \, k(u,v,w) \left|\frac{\partial(x,y,z)}{\partial (u,v,w)}\right| \,du \, dv \, dw \\[4pt] &= \iiint_G H(u,v,w) |J(u,v,w)| \, du \, dv \, dw. \end{align*}$$

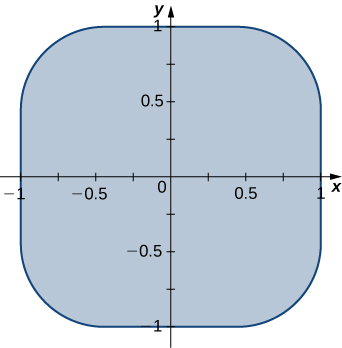
[T] Овали Ламе (або супереліпси) - це плоскі криві рівнянь$\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1$, де a, b і n є додатними дійсними числами.

a Використовуйте CAS для графіку областей,$R$ обмежених овалами Ламе для$a = 1, \, b = 2, \, n = 4$ та$n = 6$ відповідно.

b Знайдіть перетворення, які відображають область,$R$ обмежену овалом Ламе, який$x^4 + y^4 = 1$ також називається білка і графічний на наступному малюнку, в одиничний диск.

c Використовуйте CAS, щоб знайти наближення площі$A (R)$ of the region $R$ bounded by $x^4 + y^4 = 1$. Round your answer to two decimal places.

[T] Lamé ovals have been consistently used by designers and architects. For instance, Gerald Robinson, a Canadian architect, has designed a parking garage in a shopping center in Peterborough, Ontario, in the shape of a superellipse of the equation $\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1$ with $\frac{a}{b} = \frac{9}{7}$ and $n = e$. Use a CAS to find an approximation of the area of the parking garage in the case $a = 900$ yards, $b = 700$ yards, and $n = 2.72$ yards.

[Hide Solution]

$A(R) \simeq 83,999.2$

Chapter Review Exercises

True or False? Justify your answer with a proof or a counterexample.

$$\int_a^b \int_c^d f(x,y) \, dy \, dx = \int_c^d \int_a^b f(x,y) \, dy \, dx \nonumber$$

Fubini’s theorem can be extended to three dimensions, as long as $f$ is continuous in all variables.

[Hide solution]

True.

The integral $$\int_0^{2\pi} \int_0^1 \int_0^1 dz \, dr \, d\theta \nonumber$$ represents the volume of a right cone.

The Jacobian of the transformation for $x = u^2 - 2v, \, y = 3v - 2uv$ is given by $-4u^2 + 6u + 4v$.

[Hide Solution]

False.

Evaluate the following integrals.

$$\iint_R (5x^3y^2 - y^2) \, dA, \, R = \{(x,y)|0 \leq x \leq 2, \, 1 \leq y \leq 4\} \nonumber$$

$$\iint_D \frac{y}{3x^2 + 1} dA, \, D = \{(x,y) |0 \leq x \leq 1, \, -x \leq y \leq x\} \nonumber$$

[Hide Solution]

$0$

$$\iint_D \sin (x^2 + y^2) dA \nonumber$$ where $D$ is a disk of radius $2$ centered at the origin $$\int_0^1 \int_0^1 xye^{x^2} dx \, dy \nonumber$$

[Hide Solution]

$\frac{1}{4}$

$$\int_{-1}^1 \int_0^z \int_0^{x-z} 6dy \, dx \, dz \nonumber$$

$$\iiint_R 3y \, dV, \nonumber$$ where $R = \{(x,y,z) |0 \leq x \leq 1, \, 0 \leq y \leq x, \, 0 \leq z \leq \sqrt{9 - y^2}\}$

[Hide Solution]

$1.475$

$$\int_0^2 \int_0^{2\pi} \int_r^1 r \, dz \, d\theta \, dr \nonumber$$

$$\int_0^{2\pi} \int_0^{\pi/2} \int_1^3 \rho^2 \, \sin(\varphi) d\rho \, d\varphi, \, d\theta \nonumber$$

[Hide Solution]

$\frac{52}{3} \pi$

$$\int_0^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-\sqrt{1-x^2-y^2}}^{\sqrt{1-x^2-y^2}} dz \, dy \, sx \nonumber$$

For the following problems, find the specified area or volume.

The area of region enclosed by one petal of $r = \cos (4\theta)$.

[Hide Solution]

$\frac{\pi}{16}$

The volume of the solid that lies between the paraboloid $z = 2x^2 + 2y^2$ and the plane $z = 8$.

The volume of the solid bounded by the cylinder $x^2 + y^2 = 16$ and from $z = 1$ to $z + x = 2$.

[Hide Solution]

$93.291$

The volume of the intersection between two spheres of radius 1, the top whose center is $(0,0,0.25)$ and the bottom, which is centered at $(0,0,0)$.

For the following problems, find the center of mass of the region.

$\rho(x,y) = xy$ on the circle with radius $1$ in the first quadrant only.

[Hide Solution]

$\left(\frac{8}{15}, \frac{8}{15}\right)$

$\rho(x,y) = (y + 1) \sqrt{x}$ in the region bounded by $y = e^x, \, y = 0$, and $x = 1$.

$\rho(x,y,z) = z$ on the inverted cone with radius $2$ and height $2$.

$\left(0,0,\frac{8}{5}\right)$

The volume an ice cream cone that is given by the solid above $z = \sqrt{(x^2 + y^2)}$ and below $z^2 + x^2 + y^2 = z$.

The following problems examine Mount Holly in the state of Michigan. Mount Holly is a landfill that was converted into a ski resort. The shape of Mount Holly can be approximated by a right circular cone of height $1100$ ft and radius $6000$ ft.

If the compacted trash used to build Mount Holly on average has a density $400 \, lb/ft^3$, find the amount of work required to build the mountain.

[Hide Solution]

$1.452 \pi \times 10^{15}$ ft-lb

In reality, it is very likely that the trash at the bottom of Mount Holly has become more compacted with all the weight of the above trash. Consider a density function with respect to height: the density at the top of the mountain is still density $400 \, lb/ft^3$ and the density increases. Every $100$ feet deeper, the density doubles. What is the total weight of Mount Holly?

The following problems consider the temperature and density of Earth’s layers.

[T] The temperature of Earth’s layers is exhibited in the table below. Use your calculator to fit a polynomial of degree $3$ to the temperature along the radius of the Earth. Then find the average temperature of Earth. (Hint: begin at $0$ in the inner core and increase outward toward the surface)

Layer	Depth from center (km)	Temperature $^oC$
Rocky Crust	0 to 40	0
Upper Mantle	40 to 150	870
Mantle	400 to 650	870
Inner Mantel	650 to 2700	870
Molten Outer Core	2890 to 5150	4300
Inner Core	5150 to 6378	7200

Source: http://www.enchantedlearning.com/sub...h/Inside.shtml

[Hide Solution]

$y = -1.238 \times 10^{-7} x^3 + 0.001196 x^2 - 3.666x + 7208$; average temperature approximately $2800 ^oC$

[T] The density of Earth’s layers is displayed in the table below. Using your calculator or a computer program, find the best-fit quadratic equation to the density. Using this equation, find the total mass of Earth.

Layer	Depth from center (km)	Density $(g/cm^3)$
Inner Core	0	12.95
Outer Core	1228	11.05
Mantle	3488	5.00
Upper Mantle	6338	3.90
Crust	6378	2.55

Source: http://hyperphysics.phy-astr.gsu.edu...rthstruct.html

The following problems concern the Theorem of Pappus (see Moments and Centers of Mass for a refresher), a method for calculating volume using centroids. Assuming a region $R$, when you revolve around the $x$-axis the volume is given by $V_x = 2\pi A \bar{y}$, and when you revolve around the $y$-axis the volume is given by $V_y = 2\pi A \bar{x}$, where $A$ is the area of $R$. Consider the region bounded by $x^2 + y^2 = 1$ and above $y = x + 1$.

Find the volume when you revolve the region around the $x$-axis.

[Hide Solution]

$\frac{\pi}{3}$

Find the volume when you revolve the region around the $y$-axis.

Glossary

Jacobian

the Jacobian $J (u,v)$ in two variables is a $2 \times 2$ determinant:

$$J(u,v) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \end{vmatrix}; \nonumber$$

the Jacobian $J (u,v,w)$ in three variables is a $3 \times 3$ determinant:

$$J(u,v,w) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \frac{\partial z}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \frac{\partial z}{\partial v} \nonumber \\ \frac{\partial x}{\partial w} \frac{\partial y}{\partial w} \frac{\partial z}{\partial w}\end{vmatrix} \nonumber$$

one-to-one transformation

a transformation $T : G \rightarrow R$ defined as $T(u,v) = (x,y)$ is said to be one-to-one if no two points map to the same image point

planar transformation

a function $T$ that transforms a region $G$ in one plane into a region $R$ in another plane by a change of variables

transformation

a function that transforms a region GG in one plane into a region RR in another plane by a change of variables