15.1: Подвійні інтеграли над прямокутними областями
- Page ID
- 61964
- Визнайте, коли функція двох змінних інтегрується над прямокутною областю.
- Розпізнавати та використовувати деякі властивості подвійних інтегралів.
- Оцініть подвійний інтеграл над прямокутною областю, записуючи його як ітераційний інтеграл.
- Використовуйте подвійний інтеграл для обчислення площі області, об'єму під поверхнею або середнього значення функції над площиною області.
У цьому розділі ми досліджуємо подвійні інтеграли і покажемо, як ми можемо використовувати їх для знаходження об'єму твердого тіла над прямокутною областю в xy-площині. Багато властивостей подвійних інтегралів подібні до тих, які ми вже обговорювали для одиночних інтегралів.
Обсяги та подвійні інтеграли
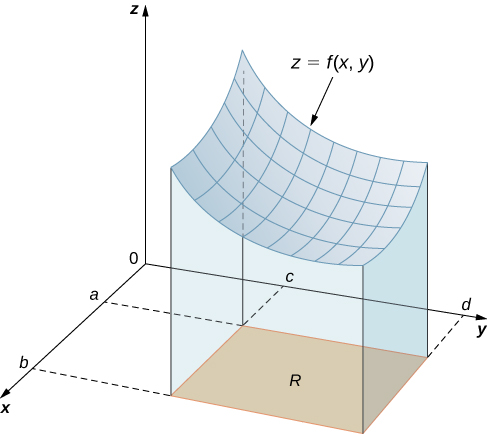
Починаємо з розгляду простору над прямокутною областю\(R\). Розглянемо неперервну функцію\(f(x,y)≥0\) двох змінних, визначених на замкнутому прямокутнику\(R\):
\[R=[a,b] \times [c,d]= \left\{(x,y) ∈ \mathbb{R}^2| \, a ≤ x ≤ b, \, c ≤ y ≤ d \right\} \nonumber \]
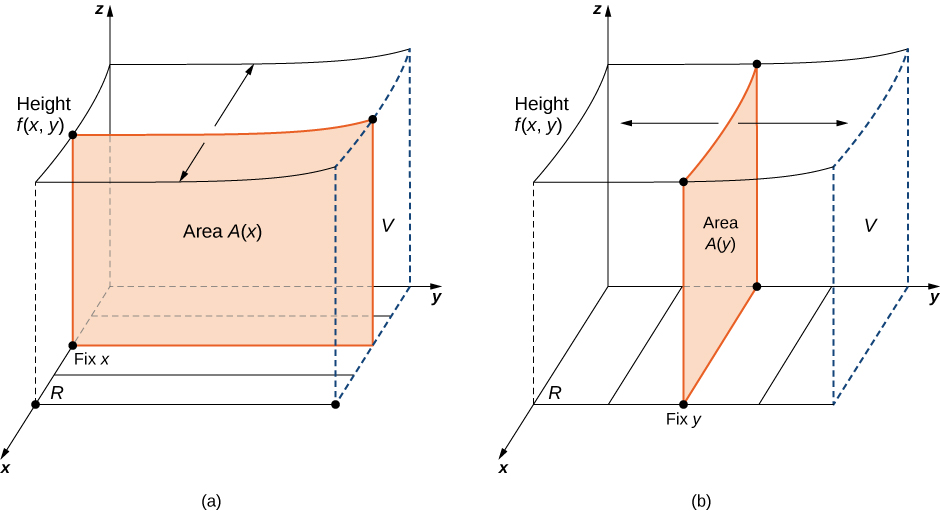
Тут\([a,b] \times [c,d]\) позначається декартове добуток двох замкнутих інтервалів\([a,b]\) і\([c,d]\). Він складається з прямокутних пар\((x,y)\) таких, що\(a≤x≤b\) і\(c≤y≤d\). Графік\(f\) являє собою поверхню над\(xy\) -площиною з рівнянням,\(z = f(x,y)\) де\(z\) висота поверхні в точці\((x,y)\). \(S\)Дозволяти тверде тіло, яке лежить вище\(R\) і під графіком\(f\) (рис.\(\PageIndex{1}\)). Основою твердого тіла є прямокутник\(R\) у\(xy\) -площині. Ми хочемо знайти обсяг\(V\) твердого тіла\(S\).
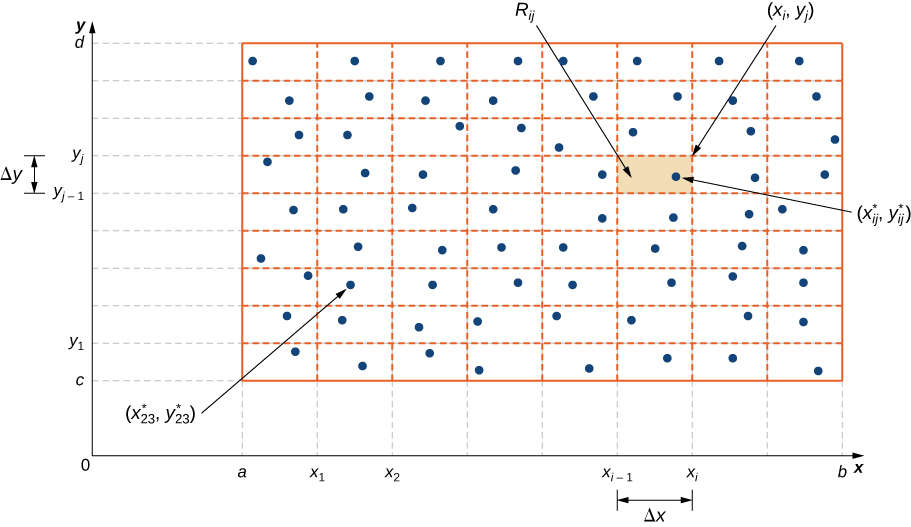
Ділимо область\(R\) на невеликі прямокутники\(R_{ij}\), кожен з площею\(ΔA\) і зі сторонами\(Δx\) і\(Δy\) (рис.\(\PageIndex{2}\)). Робимо це, розділивши інтервал\([a,b]\) на\(m\) підінтервали і розділивши інтервал\([c,d]\) на\(n\) субінтервали. Значить\(\Delta x = \frac{b - a}{m}\)\(\Delta y = \frac{d - c}{n}\), і\(\Delta A = \Delta x \Delta y\).
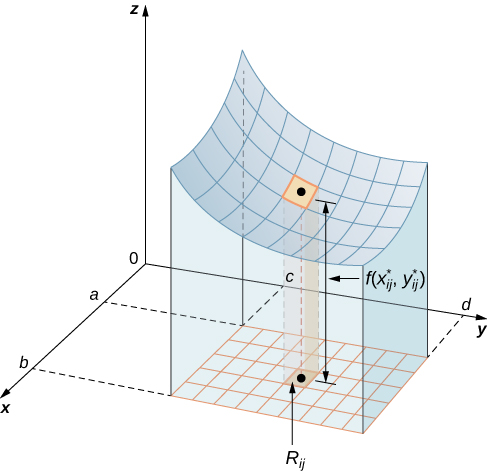
Обсяг тонкої прямокутної коробки вище\(R_{ij}\)\(f(x_{ij}^*, \, y_{ij}^*)\,\Delta A\), де (\(x_{ij}^*, \, y_{ij}^*\)) - довільна точка вибірки в кожному,\(R_{ij}\) як показано на наступному малюнку,\(f(x_{ij}^*, \, y_{ij}^*)\) - це висота відповідної тонкої прямокутної коробки і\(\Delta A\) площа кожного прямокутника\(R_{ij}\).
Використовуючи ту ж ідею для всіх підпрямокутників, отримаємо приблизний об'єм твердого тіла S як
\[V \approx \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Ця сума відома як подвійна сума Рімана і може бути використана для наближення значення об'єму твердого тіла. Тут подвійна сума означає, що для кожного підпрямокутника ми оцінюємо функцію в обраній точці, множимо на площу кожного прямокутника, а потім додаємо всі результати.
Як ми бачили в однозмінному випадку, ми отримуємо краще наближення до фактичного обсягу, якщо\(m\) і\(n\) станете більше.
\[V = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*) \Delta A \nonumber \]
або
\[V=\lim_{\Delta x, \, \Delta y \rightarrow 0} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Зверніть увагу, що сума наближається до межі в будь-якому випадку, а межа - об'єм твердого тіла з основою\(R\). Тепер ми готові визначити подвійний інтеграл.
Подвійний інтеграл функції\(f(x, \, y)\) над прямокутною\(R\) областю в\(xy\) -площині визначається як
\[\iint_R f(x, \, y) dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, \, y_{ij}^*)\Delta A. \nonumber \]
Якщо\(f(x,y)\geq 0\), then the volume \(V\) of the solid \(S\), which lies above \(R\) in the \(xy\)-plane and under the graph of \(f\), is the double integral of the function \(f(x,y)\) over the rectangle \(R\). If the function is ever negative, then the double integral can be considered a “signed” volume in a manner similar to the way we defined net signed area in певний інтеграл.
Розглянемо функцію\(z = f(x, \, y) = 3x^2 - y\) над прямокутною областю\(R = [0, 2] \times [0, 2]\) (рис.\(\PageIndex{4}\)).
- Налаштуйте подвійний інтеграл для знаходження значення знакового об'єму твердого тіла\(S\), що лежить над\(R\) і «під» графіком\(f\).
- \(R\)Розділіть на чотири квадрати за допомогою\(m = n = 2\) та виберіть точку вибірки як верхню праву кутову точку кожного квадрата (1,1), (2,1), (1,2) та (2,2) (рис\(\PageIndex{4}\).), щоб наблизити підписаний об'єм твердого тіла\(S\), що лежить над\(R\) та «під» графіком\(f\).
- \(R\)Розділіть на чотири квадрати з\(m = n = 2\), і виберіть точку вибірки як середину кожного квадрата: (1/2, 1/2), (3/2, 1/2), (1/2,3/2) та (3/2, 3/2), щоб наблизити підписаний обсяг.
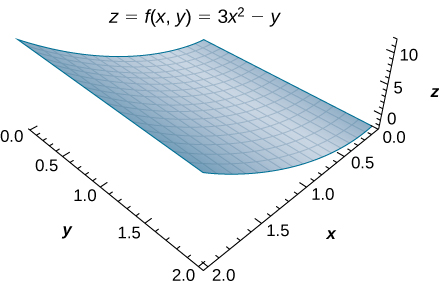
Малюнок\(\PageIndex{4}\): Функція,\(z=f(x,y)\) розміщена на графіку прямокутної області\(R=[0,2]×[0,2]\).
Рішення
- Як ми бачимо, функція\(z = f(x,y) = 3x^2 - y\) знаходиться над площиною. Щоб знайти підписаний обсяг\(S\), нам потрібно\(R\) розділити область на маленькі прямокутники\(R_{ij}\), кожен з яких має площу\(ΔA\) і зі сторонами\(Δx\) і\(Δy\), і вибрати в\((x_{ij}^*, y_{ij}^*)\) якості вибіркових точок в кожному\(R_{ij}\). Отже, подвійний інтеграл встановлюється як
\[V = \iint_R (3x^2 - y) dA = \lim_{m,n→∞} \sum_{i=1}^m \sum_{j=1}^n [3(x_{ij}^*)^2 - y_{ij}^*] \Delta A. \nonumber \]
- Наближення підписаного обсягу за допомогою суми Рімана з\(m = n = 2\) ми маємо\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). Крім того, вибірковими точками є (1, 1), (2, 1), (1, 2) та (2, 2), як показано на наступному малюнку.
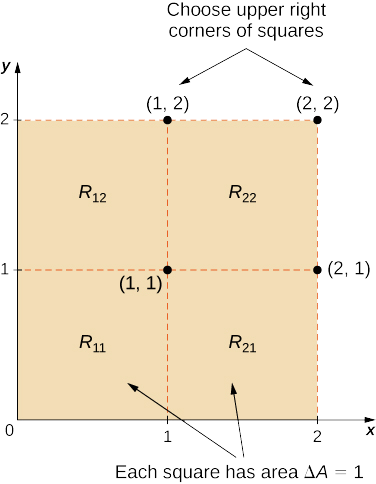
Отже,
\ [\ почати {вирівнювати*} V &\ приблизно\ сума_ {i = 1} ^2\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Дельта А\\ [4пт]
&=\ сума {i = 1} ^2 (f (x_ {i1} ^*, y_ {i1} ^*, y_ {i1} ^*) (x_ {i2} ^*, y_ {i2} ^*))\ Дельта A\\ [4pt]
&=f (x_ {11} ^*, y_ {11} ^*)\ Дельта А + f (x_ {21} ^*, y_ {21} ^*)\ Дельта А + f (x_ {12} ^*, y_ {12} ^*) Дельта А + f (x_ {22} ^*, y_ {22} ^*)\ Дельта А\\ [4пт]
&= f (1,1) (1) + f (2,1) (1) + f (1,2) (1) + f (2,2) (1)\\ [4pt]
&= (3 - 1) (1) + (12 - 1) (1) + (1) + (1) + (1) + (3 - 2)) (1) + (12 - 2) (1)\\ [4пт]
&= 2 + 11 + 1 + 10 = 24. \ end {вирівнювати*}\]
- Наближення підписаного обсягу за допомогою суми Рімана з\(m = n = 2\) ми маємо\(\Delta A = \Delta x \Delta y = 1 \times 1 = 1\). У цьому випадку точки вибірки є (1/2, 1/2), (3/2, 1/2), (1/2, 3/2) та (3/2, 3/2).
Отже,
\ [\ begin {align*} V &\ приблизно\ sum_ {i = 1} ^2\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Дельта A\\ [4pt]
&=f (x_ {11} ^*, y_ {11} ^*)\ Дельта A + f (x_ {21} ^*, y_ {21} ^*)\ Дельта А + f (x_ {12} ^*, y_ {12} ^*)\ Дельта А + f (x_ {22} ^*, y_ {22} ^*)\ Дельта А\\ [4pt]
&= f (1/2,1/2) (1) + f (3/2,1/2) (1) + f (1/2,3/2) (1) + f (3/2,3/2) (1)\\ [4pt]
&=\ лівий (\ frac {3} {4} {1} {4}\ правий) (1) +\ лівий (\ frac {27} {4}\ правий) (1) +\ лівий (\ frac {27} {4}\ гідророзрив {1} {2}\ праворуч) (1) +\ ліворуч (\ frac {3} {4} -\ frac {3} {2}\ праворуч) (1) +\ ліворуч (\ frac {27} {4} -\ frac {3} {2}\ праворуч) (1)\\ [4pt]
&=\ гідророзриву {2} {4} +\ гідророзриву {25} {4} +\ ліворуч (-\ гідророзриву {3} {4}\ праворуч) +\ гідророзриву {21} {4} =\ гідророзриву {45} {4} = 11. \ end {вирівнювати*}\]
Аналіз
Зверніть увагу, що приблизні відповіді відрізняються через вибір точок вибірки. У будь-якому випадку ми вводимо деяку помилку, оскільки ми використовуємо лише кілька вибіркових точок. Таким чином, нам потрібно дослідити, як ми можемо досягти точної відповіді.
Скористайтеся тією ж\(z = f(x, y) = 3x^2 - y\) функцією для прямокутної області\(R=[0,2]×[0,2]\).
\(R\)Розділіть на ті ж чотири квадрати з\(m = n = 2\), і виберіть точки вибірки як верхню ліву кутову точку кожного квадрата (0,1), (1,1), (0,2) та (1,2) (рис\(\PageIndex{5}\).), щоб наблизити підписаний об'єм твердого тіла\(S\), що лежить вище\(R\) та «під» графіком\(f\).
- Підказка
-
Дотримуйтесь кроків попереднього прикладу.
- Відповідь
-
\[V \approx \sum_{i=1}^2 \sum_{j=1}^2 f(x_{ij}^*, y_{ij}^*)\,\Delta A = 0 \nonumber \]
Зауважимо, що ми розробили концепцію подвійного інтеграла з використанням прямокутної області\(R\). Це поняття можна поширити на будь-який загальний регіон. Однак, коли область не прямокутна, підпрямокутники можуть не всі ідеально вписуватися\(R\), особливо якщо базова область вигнута. Розглянемо цю ситуацію більш детально в наступному розділі, де ми вивчаємо області, які не завжди прямокутні і підпрямокутники можуть не ідеально вписуватися в регіон\(R\). Також висоти можуть бути не точними, якщо поверхня\(z=f(x,y)\) вигнута. Однак похибки з боків і висота, де шматки можуть не вписатися ідеально в межах твердого\(S\) підходу 0 як\(m\) і наблизитися\(n\) до нескінченності. Також подвійний інтеграл функції\(z=f(x,y)\) існує за умови, що функція не\(f\) надто переривчаста. Якщо функція обмежена і безперервна над\(R\) за винятком скінченного числа гладких кривих, то подвійний інтеграл існує, і ми говоримо, що ff інтегрується над\(R\).
Так як\(\Delta A = \Delta x \Delta y = \Delta y \Delta x\), ми можемо висловити\(dA\) як\(dx \, dy\) або\(dy \, dx\). Це означає, що, коли ми використовуємо прямокутні координати, подвійний інтеграл над областю,\(R\) позначеною
\[\iint_R f(x,y)\,dA \nonumber \]
можна записати як
\[\iint_R f(x,y)\,dx\,dy \nonumber \]
або
\[\iint_R f(x,y)\,dy\,dx. \nonumber \]
Тепер давайте перерахуємо деякі властивості, які можуть бути корисними для обчислення подвійних інтегралів.
Властивості подвійних інтегралів
Властивості подвійних інтегралів дуже корисні при їх обчисленні або іншій роботі з ними. Ми перерахуємо тут шість властивостей подвійних інтегралів. Властивості 1 і 2 іменуються як лінійність інтеграла, властивість 3 - адитивність інтеграла, властивість 4 - монотонність інтеграла, а властивість 5 використовується для знаходження меж інтеграла. Властивість 6 використовується, якщо\(f(x,y)\) є добутком двох функцій\(g(x)\) і\(h(y)\).
Припустимо, що функції\(f(x,y)\) і\(g(x,y)\) інтегруються по прямокутній області\(R\);\(S\) і\(T\) є субрегіонами\(R\); і припустимо, що\(m\) і\(M\) є дійсними числами.
- Сума\(f(x,y)+g(x,y)\) інтегрується і
\[\iint_R [f(x, y) + g(x, y)]\,dA = \iint_R f(x,y)\, dA + \iint_R g(x, y) \,dA. \nonumber \]
- Якщо c - константа, то\(cf(x,y)\) інтегрується і
\[\iint_R cf(x,y)\,dA = c\iint_R f(x,y)\,dA. \nonumber \]
- Якщо\(R=S∪T\) і\(S∩T=∅\) крім перекриття на кордоні, то
\[\iint_R f(x,y)\,dA = \iint_S f(x,y) \,dA + \iint_T f(x,y)\, dA. \nonumber \]
- Якщо\(f(x,y) \geq g(x,y)\) для\((x,y)\) в\(R\), то
\[\iint_R f(x,y)\,dA \geq \iint_R g(x,y)\,dA. \nonumber \]
- Якщо\(m \leq f(x,y) \leq M\) і\(A(R) = \, \text{the area of}\,R\), то
\[m \cdot A(R) \leq \iint_R f(x,y)\,dA \leq M \cdot A(R). \nonumber \]
- У разі, коли\(f(x,y)\) може бути врахований як\(g(x)\) добуток функції\(x\) тільки і функції\(h(y)\)\(y\) тільки, то над\(R = \big\{(x,y) \,|\,a \leq x \leq b, \, c \leq y \leq d \big\}\) областю, подвійний інтеграл може бути записаний як
\[\iint_R f(x,y)\,dA = \left(\int_a^b g(x)\,dx \right)\left(\int_c^d h(y) \,dy \right). \nonumber \]
Ці властивості використовуються при оцінці подвійних інтегралів, як ми побачимо пізніше. Ми станемо кваліфікованими у використанні цих властивостей, як тільки ознайомимося з обчислювальними інструментами подвійних інтегралів. Отже, давайте перейдемо до цього зараз.
Ітераційні інтеграли
Поки що ми бачили, як налаштувати подвійний інтеграл і як отримати приблизне значення для нього. Ми також можемо уявити, що оцінка подвійних інтегралів за допомогою визначення може бути дуже тривалим процесом, якщо ми вибираємо більші значення для\(m\)\(n\) і.Тому нам потрібна практична і зручна техніка для обчислення подвійних інтегралів. Іншими словами, нам потрібно навчитися обчислювати подвійні інтеграли, не використовуючи визначення, яке використовує межі та подвійні суми.
Основна ідея полягає в тому, що оцінка стає простішою, якщо ми можемо розбити подвійний інтеграл на одиничні інтеграли шляхом інтеграції спочатку по відношенню до однієї змінної, а потім по відношенню до іншої. Ключовий інструмент, який нам потрібен, називається ітераційним інтегралом.
Припустимо\(a\)\(b\),,\(c\), і\(d\) є дійсними числами. Визначено ітераційний інтеграл для функції\(f(x,y)\) над прямокутною областю\(R =[a,b]×[c,d]\) як
\[\int_a^b\int_c^d f(x,y)\,dy \, dx = \int_a^b \left[\int_c^d f(x,y)\,dy \right] dx \nonumber \]
або
\[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d \left[\int_a^b f(x,y)\,dx \right] dy. \nonumber \]
Позначення\(\int_a^b \left[\int_c^d f(x,y)\,dy \right] dx\) означає, що ми інтегруємо\(f(x,y)\) стосовно,\(y\) утримуючи\(x\) постійну. Аналогічно, позначення\(\int_c^d \left[\int_a^b f(x,y)\,dx \right] dy\) означає, що ми інтегруємо\(f(x,y)\) стосовно,\(x\) утримуючи\(y\) постійну. Той факт, що подвійні інтеграли можна розділити на ітераційні інтеграли, виражається в теоремі Фубіні. Подумайте про цю теорему як про важливий інструмент для оцінки подвійних інтегралів.
Припустимо, що\(f(x,y)\) це функція двох змінних, яка є безперервною над прямокутної області\(R = \big\{(x,y) ∈ \mathbb{R}^2 | \, a \leq x \leq b, \, c \leq y \leq d \big\}\). Тоді ми бачимо з малюнка\(\PageIndex{6}\), що подвійний інтеграл\(f\) над областю дорівнює ітераційний інтеграл,
\[\iint_R f(x,y)\,dA = \iint_R f(x,y)\,dx \, dy = \int_a^b \int_c^d f(x,y)\,dy \, dx = \int_c^d \int_a^b f(x,y)\,dx \, dy. \nonumber \]
Більш загально теорема Фубіні є істинною, якщо\(f\) вона обмежена\(R\) і\(f\) є переривчастою лише на скінченній кількості неперервних кривих. Іншими словами,\(f\) має бути інтегрованим над\(R\).
Використовуйте теорему Фубіні для обчислення подвійного інтеграла\(\displaystyle \iint_R f(x,y) \,dA\) де\(f(x,y) = x\) і\(R = [0, 2] \times [0, 1]\).
Рішення
Теорема Фубіні пропонує простіший спосіб оцінки подвійного інтеграла за допомогою ітераційного інтеграла. Зверніть увагу, як граничні значення регіону\(R\) стають верхньою і нижньою межею інтеграції.
\ [\ почати {вирівнювати*}\ iInt_R f (x, y)\, Да &=\ iInt_R f (x, y)\, дх\, ди\\ [4pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {x = 0} ^ {x
= 2} x\, dx\, dx\, dy\\ [4pt] &int_ _ {y=0} ^ {y=1}\ лівий [\ розрив {x^2} {2}\ bigg|_ {x = 0} ^ {x = 2}\ праворуч]\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=1} 2\, dy = 2y\ bigg|_ {y=0 } ^ {y=1} = 2\ кінець {вирівнювати*}\]
Подвійна інтеграція в цьому прикладі досить проста, щоб безпосередньо використовувати теорему Фубіні, що дозволяє нам перетворити подвійний інтеграл в ітераційний інтеграл. Отже, тепер ми готові перетворити всі подвійні інтеграли в ітераційні інтеграли і продемонструвати, як перераховані раніше властивості можуть допомогти нам оцінити подвійні інтеграли, коли функція\(f(x,y)\) є більш складною. Зверніть увагу, що порядок інтеграції може бути змінений (див. Приклад 7).
Оцініть подвійний інтеграл\[\iint_R (xy - 3xy^2) \,dA, \, \text{where} \, R = \big\{(x,y) \,| \, 0 \leq x \leq 2, \, 1 \leq y \leq 2 \big\}.\nonumber \]
Рішення
Ця функція має дві частини: одна частина є,\(xy\) а інша\(3xy^2\). Також другий шматок має постійну 3. Зверніть увагу, як ми використовуємо властивості i та ii, щоб допомогти оцінити подвійний інтеграл.
\ [\ begin {align*}\ iInt_R (xy - 3xy^2)\, dA &=\ iInt_r xy\, dA +\ iInt_r (-3xy^2)\, dA &\ text {Властивість i: Інтеграл суми - сума інтегралів.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2}\ int_ {x=0} ^ {x=2} xy\, dx\, dx\, dy -\ int_ {y=1} ^ {y=2}\ int_ {x=0} ^ {x=2} 3xy^2\, dx\, dy &\ text {Перетворення подвійних інтегралів на ітераційні інтеграли.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2}\ лівий (\ frac {x^2} {2} y\ праворуч)\ bigg|_ {x=0} ^ {x=2}\, dy - 3\ int_ {y=1} ^ {y=2}\ left (\ frac x^2} {2} y^2\ праворуч)\ bigg|_ {x=0} ^ {x=2}\, dy &\ text {Інтеграція стосовно $x$, утримуючи $ y$ константу.}\\ [4pt]
&=\ int_ {y=1} ^ {y=2} 2y\, dy -\ int_ {y=1} ^ {y=2} 6y^2 dy &\ text {Властивість ii: Розміщення константи перед інтегралом.}\\ [4pt]
&= 2\ int_1^2 y\, dy - 6\ int_1^2 y^2 {Інтеграція щодо y.}\\ [4pt]
&= 2\ розриву {y^2} {2}\ bigg|_1^2 - 6\ розрив {y^3} {3}\ bigg|_1^2\\ [4pt]
&=y^2\ bigg|_1^2 - 2y^3\ big|_1^2\\ [4pt]
& =( 4−1) − 2 (8−1) = 3 − 2 (7) = 3 − 14 = −11. \ end {вирівнювати*}\]
Над\(R = \big\{(x,y)\,| \, 1 \leq x \leq 3, \, 1 \leq y \leq 2 \big\}\) регіоном ми маємо\(2 \leq x^2 + y^2 \leq 13\). Знайти нижню і верхню межу для інтеграла\(\displaystyle \iint_R (x^2 + y^2)\,dA.\)
Рішення
Для нижньої межі інтегруйте постійну функцію 2 над областю\(R\). Для верхньої межі інтегруйте постійну функцію 13 над областю\(R\).
\[\begin{align*} \int_1^2 \int_1^3 2 \,dx \, dy &= \int_1^2 [2x\bigg|_1^3] \,dy = \int_1^2 2(2)dy = 4y\bigg|_1^2 = 4(2 - 1) = 4 \\[4pt] \int_1^2 \int_1^3 13dx \, dy &= \int_1^2 [13x\bigg|_1^3] \,dy = \int_1^2 13(2)\,dy = 26y\bigg|_1^2 = 26(2 - 1) = 26. \end{align*}\]
Значить, отримуємо\(\displaystyle 4 \leq \iint_R (x^2 + y^2) \,dA \leq 26.\)
Оцініть\(\displaystyle \iint_R e^y \cos x \, dA\) інтеграл по регіону\(R = \big\{(x,y)\,| \, 0 \leq x \leq \frac{\pi}{2}, \, 0 \leq y \leq 1 \big\}\).
Рішення
Це чудовий приклад для властивості vi, оскільки функція явно\(f(x,y)\) є добутком двох однозмінних функцій\(e^y\) і\(\cos x\). Таким чином, ми можемо розділити інтеграл на дві частини, а потім інтегрувати кожну з них як проблему інтеграції однієї змінної.
\ [\ begin {align*}\ iInt_r e^y\ cos x\, Да &=\ int_0^1\ int_0^ {\ pi/2} e^y\ cos x\, dx\, dh\\ [4pt]
&=\ вліво (\ int_0^1 e^y ди\ вправо)\ вліво (\ int_0^ {\ pi/2}\ cos x, дх\ праворуч)\\ [4pt]
&= (e^y\ bigg|_0^1) (\ sin x\ bigg|_0^ {\ pi/2})\\ [4pt]
&= e - 1. \ end {вирівнювати*}\]
a. використовувати властивості подвійного інтеграла та теореми Фубіні для оцінки інтеграла
\[\int_0^1 \int_{-1}^3 (3 - x + 4y) \,dy \, dx. \nonumber \]
б Покажіть, що\(\displaystyle 0 \leq \iint_R \sin \pi x \, \cos \pi y \, dA \leq \frac{1}{32}\) де\(R = \left(0, \frac{1}{4}\right)\left(\frac{1}{4}, \frac{1}{2}\right)\).
- Підказка
-
Використовуйте властивості i. і ii. і оцініть ітераційний інтеграл, а потім використовуйте властивість v.
- Відповідь
-
а.\(26\)
b Відповіді можуть відрізнятися.
Як ми вже згадували раніше, коли ми використовуємо прямокутні координати, подвійний інтеграл над областю,\(R\) позначеною,\(\iint_R f(x,y) \, dA\) може бути записаний як\(\iint_R\, f(x,y) \, dx \, dy\) або\(\iint_R \, f(x,y) \,dy \, dx.\) Наступний приклад показує, що результати однакові незалежно від того, який порядок інтеграції ми вибираємо.
Повернемося до функції\(f(x,y) = 3x^2 - y\) з Прикладу 1, на цей раз над прямокутною областю\(R = [0,2] \times [0,3]\). Використовуйте теорему Фубіні для оцінки\(\iint_R f(x,y) \,dA\) двома різними способами:
- Спочатку інтегрувати по відношенню до,\(y\) а потім по відношенню до\(x\);
- Спочатку інтегрувати по відношенню до,\(x\) а потім по відношенню до\(y\).
Рішення
На малюнку\(\PageIndex{6}\) показано, як працює розрахунок двома різними способами.
- Спочатку інтегруйте стосовно,\(y\) а потім інтегруйте щодо\(x\):
\ [\ почати {вирівнювати*}\ iInt_R f (x, y)\, Да &=\ int_ {x=0} ^ {x=2}\ int_ {y=0} ^ {y=3} (3x^2 - y)\, dy\, dx\\ [4pt]
&=\ int_ {x=0} ^ {x=2}\ ліво (\ int_ {y=0} ^ {y=3} (3x^2 - y)\, ди\ вправо)\, dx =\ int_ {x=0} ^ {x = 2}\ ліворуч [3x^2y -\ frac {y^2} {2}\ bigg|_ {y=0} ^ {y=3}\ праворуч]\, dx\\ [4pt]
&int=\ _ {x=0} ^ {x=2}\ лівий (9x^2 -\ розрив {9} {2}\ праворуч)\, dx = 3x^3 -\ гідророзриву {9} {2} x\ bigg|_ {x=0} ^ {x=2} = 15. \ end {вирівнювати*}\]
- Спочатку інтегруйте стосовно,\(x\) а потім інтегруйте щодо\(y\):
\ [\ begin {align*}\ iInt_R f (x, y)\, Да &=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\, dy\\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ ліворуч (\ int_ {x=0} ^ {x=2} (3x^2 - y)\, dx\ праворуч)\, dy \\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ ліворуч [x^3 - xy\ bigg|_ {x = 0} ^ {x = 2}\ праворуч] ди\\ [4pt]
&=\ int_ {y=0} ^ {y=3} (8 - 2y)\, dy = 8y - y^2\ big|_ {y=3}\, dy = 8y - y^2\ big|_ {y=3} 0} ^ {y=3} = 15. \ end {вирівнювати*}\]
Аналіз
При будь-якому порядку інтеграції, подвійний інтеграл дає нам відповідь\(15\). Ми, можливо, забажаємо інтерпретувати цю відповідь як об'єм у кубічних одиницях твердого тіла\(S\) нижче функції\(f(x,y) = 3x^2 - y\) над областю\(R = [0,2] \times [0,3]\). Однак пам'ятайте, що інтерпретація подвійного інтеграла як (незнакового) тому працює тільки тоді, коли integrand\(f\) є невід'ємною функцією над базовою областю\(R\).
Оцінити
\[\int_{y=-3}^{y=2} \int_{x=3}^{x=5} (2 - 3x^2 + y^2) \,dx \, dy. \nonumber \]
- Підказка
-
Використовуйте теорему Фубіні.
- Відповідь
-
\(-\frac{1340}{3}\)
У наступному прикладі ми бачимо, що насправді може бути корисним перемикання порядку інтеграції, щоб полегшити обчислення. Ми повернемося до цієї ідеї кілька разів в цьому розділі.
Розглянемо подвійний інтеграл\(\displaystyle \iint_R x \, \sin (xy) \, dA\) над областю\(R = \big\{(x,y) \,| \, 0 \leq x \leq \pi, \, 1 \leq y \leq 2 \big\}\) (рис.\(\PageIndex{7}\)).
- Висловіть подвійний інтеграл двома різними способами.
- Проаналізуйте, чи оцінювати подвійний інтеграл одним способом простіше іншого і чому.
- Оцініть інтеграл.
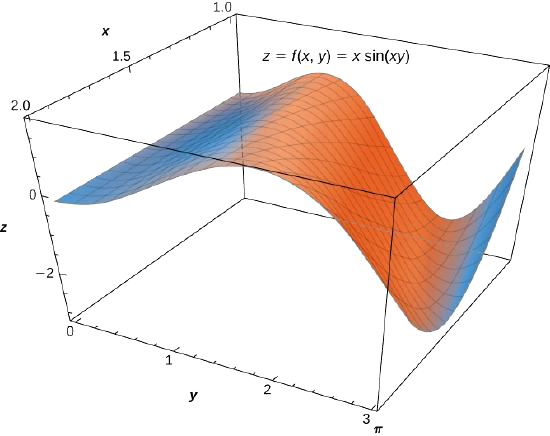
- Ми можемо висловити\(\iint_R x \, \sin (xy) \,dA\) наступними двома способами: спочатку шляхом інтеграції щодо,\(y\) а потім щодо\(x\); по-друге, інтегруючи стосовно,\(x\) а потім щодо\(y\).
\[\iint_R x \, \sin (xy) \,dA= \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \,dy \, dx \nonumber \]
Інтегруйте спочатку стосовно\(y\).
\[= \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \, \sin (xy) \,dx \, dy \nonumber \]
Інтегруйте спочатку стосовно\(x\). - Якщо ми хочемо спочатку інтегруватися щодо y, а потім інтегруватися щодо\(x\), ми бачимо, що ми можемо використовувати підміну\(u = xy\), яка дає\(du = x \, dy\). Отже, внутрішній інтеграл просто,\(\int \sin u \, du\) і ми можемо змінити межі, щоб бути функціями\(x\),
\[\iint_R x \, \sin (xy) \,dA = \int_{x=0}^{x=\pi} \int_{y=1}^{y=2} x \, \sin (xy) \, dy \, dx = \int_{x=0}^{x=\pi} \left[\int_{u=x}^{u=2x} \sin (u) \,du \right] \, dx.\nonumber \]
Однак інтеграція щодо\(x\) першого, а потім інтеграція щодо\(y\) вимагає інтеграції частинами для внутрішнього інтеграла, з\(u = x\) і\(dv = \sin(xy)dx\)
Потім\(du = dx\) і\(v = - \frac{\cos(xy)}{y}\), так
\[\iint_R x \sin(xy) \,dA = \int_{y=1}^{y=2} \int_{x=0}^{x=\pi} x \sin(xy) \,dx \, dy = \int_{y=1}^{y=2} \left[ - \frac{x \, \cos (xy)}{y} \bigg|_{x=0}^{x=\pi} + \frac{1}{y} \int_{x=0}^{x=\pi} \cos(xy)\,dx \right] \, dy.\nonumber \]
Оскільки оцінка ускладнюється, ми зробимо лише обчислення, яке простіше зробити, що, очевидно, є першим методом.
- Оцініть подвійний інтеграл, використовуючи більш простий спосіб.
\ [\ почати {вирівнювати*}\ iInt_R x\,\ sin (xy)\, Да &=\ int_ {x = 0} ^ {x=\ pi}\ int_ {y=1} ^ {y=2} x\,\ sin (xy)\, dy\, dx\\ [4pt]
&=\ int_ {x = 0} ^ {x =\ pi}\ [\ int_ {u=x} ^ {u=2x}\ sin (u)\, ду\ праворуч]\, dx =\ int_ {x = 0} ^ {x =\ пі}\ ліворуч [-\ cos u\ bigg|_ {u=x} ^ {u=2x}\ праворуч]\, dx\\ [4pt]
&=\ int _ {x = 0} ^ {x =\ пі} (-\ cos 2x +\ cos x)\, dx\\ [4pt]
&=\ лівий (-\ frac {1} {2}\ sin 2x +\ sin x\ праворуч)\ big|_ {x = 0} ^ {x =\ pi} = 0. \ end {вирівнювати*}\]
Оцініть інтеграл\(\displaystyle \iint_R xe^{xy}\,dA\) де\(R = [0,1] \times [0, \ln 5]\).
- Підказка
-
Інтеграція щодо\(y\) першого.
- Відповідь
-
\(\frac{4 - \ln 5}{\ln 5}\)
Застосування подвійних інтегралів
Подвійні інтеграли дуже корисні для знаходження площі області, обмеженої кривими функцій. Більш детально опишемо цю ситуацію в наступному розділі. Однак якщо область має прямокутну форму, ми можемо знайти її площу, інтегруючи постійну функцію\(f(x,y) = 1\) над регіоном\(R\).
Площа області\(R\) задається по\[A(R) = \iint_R 1 \, dA. \nonumber \]
Це визначення має сенс, оскільки використання\(f(x,y) = 1\) та оцінка інтеграла роблять його продуктом довжини та ширини. Давайте перевіримо цю формулу на прикладі і подивимося, як це працює.
Знайти площу області можна за\(R = \big\{\,(x,y)\,|\,0 \leq x \leq 3, \, 0 \leq y \leq 2\big\}\) допомогою подвійного інтеграла, тобто шляхом інтеграції\(1\) над регіоном\(R\).
Рішення
Область прямокутна з довжиною\(3\) і шириною\(2\), тому ми знаємо, що площа є\(6\). Ми отримуємо таку ж відповідь, коли використовуємо подвійний інтеграл:
\[A(R) = \int_0^2 \int_0^3 1 \, dx \, dy = \int_0^2 \left[x\big|_0^3\right] \, dy = \int_0^2 3 dy = 3 \int_0^2 dy = 3y\bigg|_0^2 = 3(2) = 6 \, \text{units}^2.\nonumber \]
Ми вже бачили, як подвійні інтеграли можуть бути використані для знаходження об'єму твердого тіла, обмеженого вище функцією\(f(x,y) \geq 0\) над областю,\(R\)\(f(x,y) \geq 0\) передбаченою для всіх\((x,y)\) в\(R\). Ось ще один приклад для ілюстрації цієї концепції.
Знайдіть об'єм\(V\) твердого тіла\(S\), який обмежений еліптичним параболоїдом\(2x^2 + y^2 + z = 27\), площинами\(x = 3\) та\(y = 3\) трьома координатними площинами.
Рішення
Спочатку зверніть увагу на графік поверхні на\(z = 27 - 2x^2 - y^2\) малюнку\(\PageIndex{8}\) (а) і над квадратною областю\(R_1 = [-3,3] \times [-3,3]\). Однак нам потрібен об'єм твердого тіла, обмежений еліптичним параболоїдом\(2x^2 + y^2 + z = 27\), площинами\(x = 3\) та\(y = 3\) трьома координатними площинами.
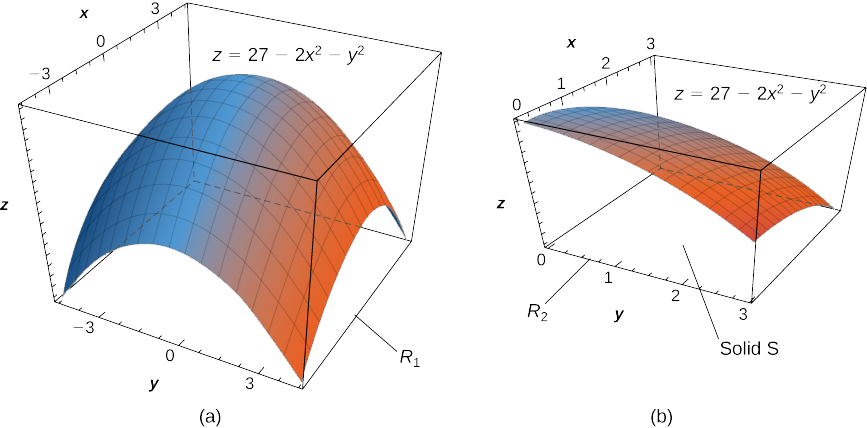
Тепер розглянемо графік поверхні на малюнку\(\PageIndex{8}\) (б). Визначаємо обсяг,\(V\) оцінюючи подвійний інтеграл над\(R_2\):
\ [\ почати {вирівнювати*} V &=\ iInt_r z\, Да =\ iInt_R (27 - 2x^2 - y^2)\, Да\\ [4pt]
&=\ int_ {y=0} ^ {y=3}\ int_ {x=0} ^ {x = 3} (27 - 2x^2 - y^2)\, dx\, dh & &\ text {Перетворити на літеральний інтеграл.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} [27x -\ frac {2} {3} x^3 - y^2x]\ bigg|_ {x=0} ^ {x = 3}\ , dy &\ text {Інтеграція стосовно $x$.}\\ [4pt]
&=\ int_ {y=0} ^ {y=3} (63 - 3y^2) dy = 63 y - y^3\ bigg|_ {y=0} ^ {y=3} = 162. \ end {вирівнювати*}\]
Знайти об'єм твердого тіла, обмеженого вище графіком\(f(x,y) = xy \sin(x^2y)\) і нижче\(xy\) -площиною на прямокутній області\(R = [0,1] \times [0,\pi]\).
- Підказка
-
Графік функції, встановіть інтеграл та використовуйте ітераційний інтеграл.
- Відповідь
-
\(\frac{\pi}{2}\)
Нагадаємо, що ми визначили середнє значення функції однієї змінної на інтервалі\([a,b]\) як
\[f_{ave} = \frac{1}{b - a} \int_a^b f(x) \, dx. \nonumber \]
Аналогічно, ми можемо визначити середнє значення функції двох змінних над регіоном \(R\). Основна відмінність полягає в тому, що ми ділимо на площу замість ширини інтервалу.
Середнє значення функції двох змінних над\(R\) областю
\[F_{ave} = \frac{1}{\text{Area of} \, R} \iint_R f(x,y)\, dx \, dy. \nonumber \]
У наступному прикладі ми знаходимо середнє значення функції над прямокутною областю. Це хороший приклад отримання корисної інформації для інтеграції шляхом проведення окремих вимірювань над сіткою, замість того, щоб намагатися знайти алгебраїчний вираз для функції.
Погодна карта на малюнку\(\PageIndex{9}\) показує незвично вологу систему шторму, пов'язану із залишками урагану «Карл», який скинув 4—8 дюймів (100—200 мм) дощу в деяких районах Середнього Заходу 22—23 вересня 2010 року. Площа опадів вимірюється 300 миль на схід на захід і 250 миль на північ на південь. Оцініть середню кількість опадів по всій площі за ці два дні.
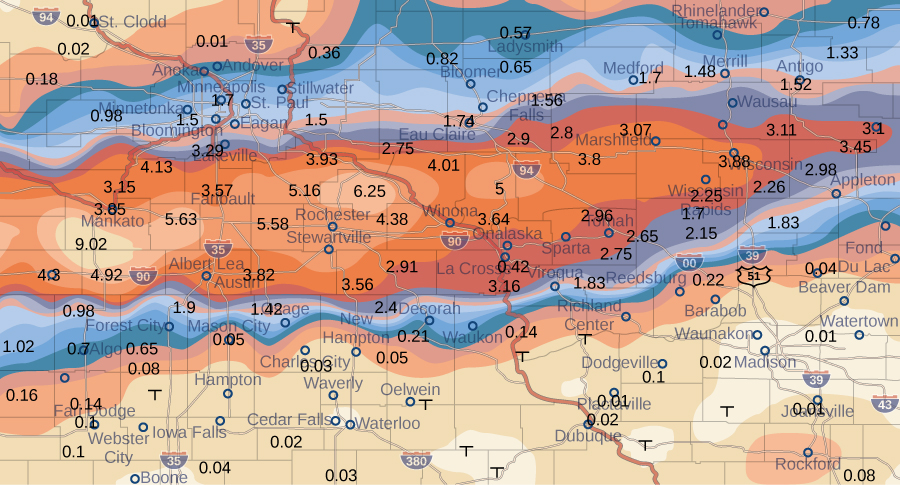
Рішення
Помістіть початок у південно-західному куті карти, щоб усі значення можна було вважати перебуватими в першому квадранті і, отже, всі позитивні. Тепер розділіть всю карту на шість прямокутників\((m = 2\) і\(n = 3)\), як показано на малюнку\(\PageIndex{9}\). Припустимо,\(f(x,y)\) позначає зливові опади в дюймах у точці приблизно в\(x\) милі на схід від\(y\) початку та милі на північ від початку. \(R\)Дозволяти представляти всю площу\(250 \times 300 = 75000\) квадратних миль. Тоді площа кожного підпрямокутника дорівнює
\[\Delta A = \frac{1}{6} (75000) = 12500.\nonumber \]
Припустімо\((x_{ij}*,y_{ij}*)\), що приблизно середні точки кожного підпрямокутника\(R_{ij}\). Зверніть увагу на область з кольоровим кодом у кожній з цих точок та оцініть кількість опадів. Кількість опадів у кожній з цих точок можна оцінити як:
- При (\(x_{11}, y_{11}\)), кількість опадів становить 0.08.
- При (\(x_{12}, y_{12}\)), кількість опадів становить 0.08.
- При (\(x_{13}, y_{13}\)), кількість опадів становить 0,01.
- При (\(x_{21}, y_{21}\)), кількість опадів становить 1.70.
- При (\(x_{22}, y_{22}\)), кількість опадів становить 1.74.
- В (\(x_{23}, y_{23}\)), кількість опадів - 3.00.
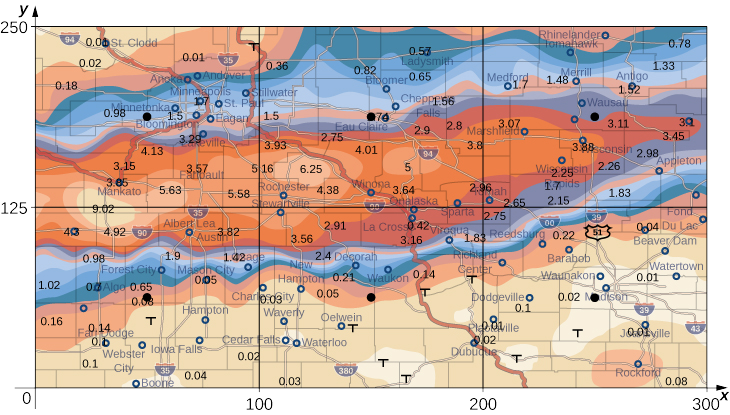
Згідно з нашим визначенням, середня зливова кількість опадів по всій площі за ці два дні становила
\ [\ почати {вирівнювати*} f_ {ave} =\ розриву {1} {Площа\, R}\ iInt_r f (x, y)\, dx\, dx\, dy &=\ розриву {1} {75000}\ iInt_R f (x, y)\, dx\, dy\\ [4pt]
&\ приблизно\ frac {1} {75000}\ сума {i=1} ^3\ sum_ {j=1} ^2 f (x_ {ij} ^*, y_ {ij} ^*)\ Дельта А\\ [4pt]
&=\ розриву {1} {75000}\ Великий [f (x_ {11} ^*, y_ {11} ^*)\ Дельта А + f (x_ {12} ^*, y_ {12} ^*)\ Дельта А + f (x_ {13} ^*, y_ {13} ^*)\ Дельта А + f (x_ {21} ^*, y_ {21} ^*)\ Дельта А + f (x_ {22} ^*, y_ {22} ^*)\ Дельта А + f (x_ {22} ^*)\ Дельта А + f (x_ {22} ^* 23} ^*, y_ {23} ^*)\ Дельта А\ Бігг]\\ [4pt]
&\ приблизно\ гідророзриву {1} {75000}\ Великий [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Великий]\ Дельта А\\ [4pt]
&=\ розриву {1} {75000}\ Великий [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Великий] 12500\\ [4pt]
&=\ розрив {1} {6}\ Великий [0,08 + 0,08 + 0,01 + 1,70 + 1,74 + 3,00\ Великий]\\[4pt] &\approx 1.10 \;\text{in}. \end{align*}\]
Протягом 22—23 вересня 2010 року ця область мала середню грозову кількість опадів приблизно 1.10 дюймів.
Контурна карта показана для функції\(f(x,y)\) на прямокутник\(R = [-3,6] \times [-1, 4]\).

a Використовуйте правило середньої точки з\(m = 3\) і\(n = 2\) для оцінки значення\(\displaystyle \iint_R f(x,y) \,dA.\)
б Оцінити середнє значення функції\(f(x,y)\).
- Підказка
-
Розділіть область на шість прямокутників і використовуйте контурні лінії, щоб оцінити значення для\(f(x,y)\).
- Відповідь
-
Відповіді на обидві частини a. і b. можуть відрізнятися.
Ключові концепції
- Ми можемо використовувати подвійну суму Рімана для наближення об'єму твердого тіла, обмеженого вище функцією двох змінних над прямокутною областю. Приймаючи межу, це стає подвійним інтегралом, що представляє об'єм твердого тіла.
- Властивості подвійного інтеграла корисні для спрощення обчислень і пошуку меж їх значень.
- Ми можемо використовувати теорему Фубіні для написання та оцінки подвійного інтеграла як ітераційного інтеграла.
- Подвійні інтеграли використовуються для обчислення площі області, об'єму під поверхнею та середнього значення функції двох змінних над прямокутною областю.
Ключові рівняння
- \[\iint_R f(x,y) \,dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(x_ij*,y_ij*)\,ΔA\nonumber \]
- \[\int_a^b \int_c^d f(x,y)\,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \,dy \right] dx\nonumber \]або
\[\int_c^d \int_a^b f(x,y)\,dx \, dy = \int_c^d\left[ \int_a^b f(x,y) \,dx \right] dy\nonumber \]
- \[f_{ave} = \frac{1}{\text{Area of}\, R} \iint_R f(x,y) \,dx \, dy\nonumber \]
Глосарій
- подвійний інтеграл
- функції\(f(x,y)\) над областю\(R\) в\(xy\) -площині визначається як межа подвійної суми Рімана,
- \[ \iint_R f(x,y) \,dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A.\nonumber \]
- подвійна сума Рімана
- функції\(f(x,y)\) над прямокутною областю\(R\) є
- \[\sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*) \,\Delta A,\nonumber \]
- де\(R\) ділиться на менші підпрямокутники\(R_{ij}\) і\((x_{ij}^*, y_{ij}^*)\) є довільною точкою в\(R_{ij}\)
- Теорема Фубіні
- якщо\(f(x,y)\) є функцією двох змінних, яка є безперервною над прямокутною областю\(R = \big\{(x,y) \in \mathbb{R}^2 \,|\,a \leq x \leq b, \, c \leq y \leq d\big\}\), то подвійний інтеграл\(f\) над областю дорівнює ітераційному інтегралу,
- \[\displaystyle\iint_R f(x,y) \, dA = \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_c^d \int_a^b f(x,y) \,dx \, dy\nonumber \]
- ітераційний інтеграл
- для функції\(f(x,y)\) над регіоном\(R\) є
а.\(\displaystyle \int_a^b \int_c^d f(x,y) \,dx \, dy = \int_a^b \left[\int_c^d f(x,y) \, dy\right] \, dx,\)
б.\(\displaystyle \int_c^d \int_a^b f(x,y) \, dx \, dy = \int_c^d \left[\int_a^b f(x,y) \, dx\right] \, dy,\)
де\(a,b,c\), і\(d\) є будь-якими дійсними числами і\(R = [a,b] \times [c,d]\)
