15.2: Подвійні інтеграли над загальними регіонами

Цілі навчання

• Визнайте, коли функція двох змінних інтегрується над загальною областю.
• Оцінити подвійний інтеграл, обчисливши ітераційний інтеграл над областю, обмеженою двома вертикальними лініями та двома функціями\(x\), або двома горизонтальними лініями та двома функціями\(y\).
• Спростити обчислення ітераційного інтеграла, змінивши порядок інтеграції.
• Використовуйте подвійні інтеграли для обчислення об'єму області між двома поверхнями або площі площини.
• Вирішити задачі, що включають подвійні неправильні інтеграли.

Раніше ми вивчали поняття подвійних інтегралів і розглянули інструменти, необхідні для їх обчислення. Ми вивчили методи та властивості інтеграції функцій двох змінних у прямокутні області. Ми також обговорили кілька застосувань, таких як пошук обсягу, обмеженого вище функцією над прямокутною областю, пошук області шляхом інтеграції та обчислення середнього значення функції двох змінних.

У цьому розділі розглядаються подвійні інтеграли функцій, визначених над загальною обмеженою\(D\) областю на площині. Більшість попередніх результатів тримаються і в цій ситуації, але деякі методи потрібно розширити, щоб охопити цей більш загальний випадок.

Загальні регіони інтеграції

Приклад загальної обмеженої області\(D\) на площині наведено на малюнку\(\PageIndex{1}\). Оскільки\(D\) обмежений на площині, на тій же площині повинна існувати прямокутна область\(R\), яка охоплює область,\(D\) тобто прямокутна область\(R\) існує така, яка\(D\) є підмножиною\(R (D \subseteq R)\).

Малюнок\(\PageIndex{1}\): Для області,\(D\) яка є підмножиною\(R\), ми можемо\(g(x,y)\) визначити функцію рівну\(f(x,y)\) в кожній точці\(D\) і\(0\) в кожній точці\(R\) не в\(D\).

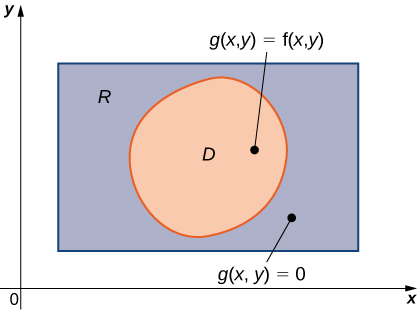
\(z = f(x,y)\)Припустимо, визначено на загальній площинній обмеженій області\(D\), як на рис\(\PageIndex{1}\). Для того, щоб розробити подвійні інтеграли\(f\) над,\(D\) ми розширюємо визначення функції, включивши всі точки прямокутної області,\(R\) а потім використовуємо поняття та інструменти з попереднього розділу. Але як ми можемо розширити визначення,\(f\) щоб включити всі пункти на\(R\)? Ми робимо це, визначаючи нову функцію\(g(x,y)\)\(R\) наступним чином:

\[g(x,y) = \begin{cases} f(x,y), & \text{if} \; (x,y) \; \text{is in}\; D \\[4pt] 0, & \text{if} \;(x,y) \; \text{is in} \; R \;\text{but not in}\; D \end{cases} \nonumber \]

Зауважте, що у нас можуть виникнути деякі технічні труднощі, якщо\(D\) межа складна. Таким чином, ми припускаємо, що межа буде кусково-гладкою і безперервною простою замкнутою кривою. Крім того, оскільки всі результати, розроблені в розділі про подвійні інтеграли над прямокутними регіонами, використовували інтегровну функцію,\(f(x,y)\) ми повинні бути обережними\(g(x,y)\) та перевіряти, що\(g(x,y)\) це інтегровна функція над прямокутною областю\(R\). Це відбувається до тих пір, поки область\(D\) обмежена простими замкнутими кривими. Наразі ми зосередимося на описі регіонів, а не на функції, і розширимо нашу теорію належним чином для інтеграції.

Розглянуто два типи плоских обмежених областей.

Визначення: Регіони типу I та типу II

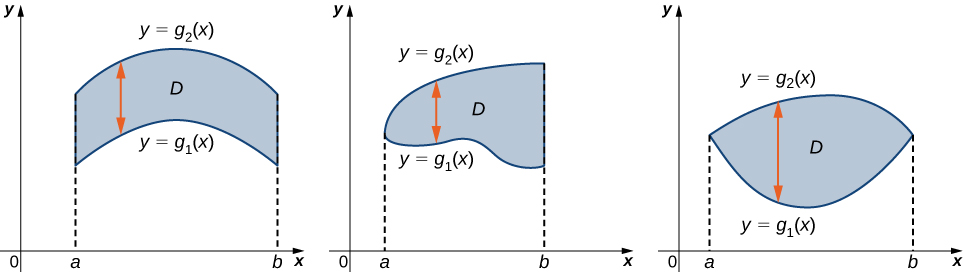
Область\(D\) в\((x,y)\) -площині має тип I, якщо вона лежить між двома вертикальними лініями та графіками двох неперервних функцій\(g_1(x)\) і\(g_2(x)\). Тобто (рис.\(\PageIndex{2}\)),

\[D = \big\{(x,y)\,|\, a \leq x \leq b, \space g_1(x) \leq y \leq g_2(x) \big\}. \nonumber \]

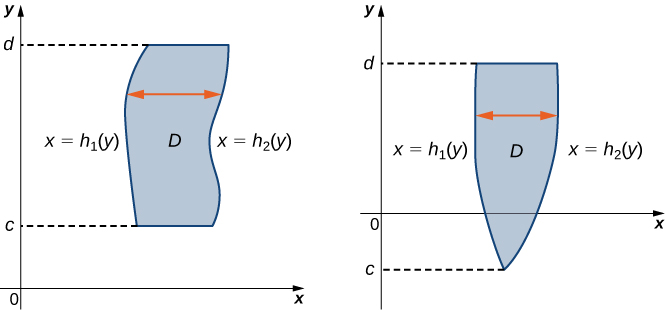
Область\(D\) в\(xy\) -площині має тип II, якщо вона лежить між двома горизонтальними лініями та графіками двох неперервних функцій\(h_1(y)\) і\(h_2(y)\). Тобто (рис.\(\PageIndex{3}\)),

\[D = \big\{(x,y)\,| \, c \leq y \leq d, \space h_1(y) \leq x \leq h_2(y) \big\}. \nonumber \]

Малюнок\(\PageIndex{2}\). Область I типу лежить між двома вертикальними лініями та графіками двох функцій\(x\).

Малюнок\(\PageIndex{3}\): Область типу II лежить між двома горизонтальними лініями та графіками двох функцій\(y\).

Приклад\(\PageIndex{1}\): Describing a Region as Type I and Also as Type II

Розглянемо область в першому квадранті між функціями\(y = \sqrt{x}\) і\(y = x^3\) (рис.\(\PageIndex{4}\)). Опишіть регіон спочатку як тип I, а потім як тип II.

Малюнок\(\PageIndex{4}\): Регіон\(D\) може бути описаний як тип I або як тип II.

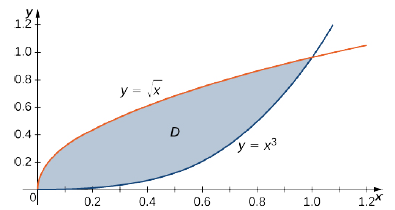
При описі регіону як типу I нам потрібно визначити функцію, яка лежить над регіоном, і функцію, яка лежить нижче області. Тут область\(D\) обмежена вище\(y = \sqrt{x}\) і нижче на\(y = x^3\) інтервал для\(x\) in\([0,1]\). Отже, як Тип I,\(D\) описується як набір\(\big\{(x,y)\,| \, 0 \leq x \leq 1, \space x^3 \leq y \leq \sqrt[3]{x}\big\}\).

Однак, описуючи регіон як тип II, нам потрібно визначити функцію, яка лежить зліва від області, і функцію, яка лежить праворуч від області. Тут область\(D\) обмежена ліворуч\(x = y^2\) і праворуч\(x = \sqrt[3]{y}\) в інтервалі для\(y\) in\([0,1]\). Отже, як тип II,\(D\) описується як набір\(\big\{(x,y) \,| \, 0 \leq y \leq 1, \space y^2 \leq x \leq \sqrt[3]{y}\big\}\).

Вправа\(\PageIndex{1}\)

Розглянемо область в першому квадранті між функціями\(y = 2x\) і\(y = x^2\). Опишіть регіон спочатку як тип I, а потім як тип II.

Підказка

Графік функцій, і малюйте вертикальні і горизонтальні лінії.

Відповідь

Тип I і Тип II виражаються як\(\big\{(x,y) \,|\, 0 \leq x \leq 2, \space x^2 \leq y \leq 2x\big\}\)\(\big\{(x,y)|\, 0 \leq y \leq 4, \space \frac{1}{2} y \leq x \leq \sqrt{y}\big\}\) і відповідно.

Подвійні інтеграли над непрямокутними областями

Щоб розробити концепцію та інструменти оцінки подвійного інтеграла над загальною, непрямокутною областю, нам потрібно спочатку зрозуміти область і вміти висловити її як тип I або тип II або комбінацію обох. Без розуміння регіонів ми не зможемо вирішити межі інтеграцій в подвійних інтегралах. В якості першого кроку розглянемо наступну теорему.

Теорема: Подвійні інтеграли над непрямокутними областями

Припустимо,\(g(x,y)\) це розширення до\(R\) прямокутника функції,\(f(x,y)\) визначеної на областях\(D\) і\(R\) як показано на малюнку\(\PageIndex{1}\) всередині\(R\). Потім\(g(x,y)\) інтегрується, і ми визначаємо подвійний\(D\) інтеграл\(f(x,y)\) над

\[\iint\limits_D f(x,y) \,dA = \iint\limits_R g(x,y) \,dA. \nonumber \]

Права частина цього рівняння - це те, що ми бачили раніше, тому ця теорема є розумною, оскільки\(R\) є прямокутником і\(\iint\limits_R g(x,y)dA\) обговорювалася в попередньому розділі. Крім того, рівність працює тому, що значення\(g(x,y)\) є\(0\) для будь-якої точки\((x,y)\), яка лежить зовні,\(D\) і, отже, ці точки нічого не додають до інтеграла. Однак важливо, щоб прямокутник\(R\) містив область\(D\).

Насправді, якщо область\(D\) обмежена плавними кривими на площині, і ми можемо описати її як тип I або тип II або суміш обох, то ми можемо використовувати наступну теорему і не потрібно знаходити прямокутник,\(R\) що містить область.

Теорема: Теорема Фубіні (сильна форма)

Для функції\(f(x,y)\), яка є безперервною на області\(D\) типу I, ми маємо

\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y)\,dy \right] dx. \nonumber \]

Аналогічно, для функції\(f(x,y)\), яка є безперервною на області\(D\) типу II, ми маємо

\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dx \space dy = \int_c^d \left[\int_{h_1(y)}^{h_2(y)} f(x,y)\,dx \right] dy. \nonumber \]

Інтеграл у кожному з цих виразів є ітераційним інтегралом, подібним до тих, які ми бачили раніше. Зверніть увагу, що у внутрішньому інтегралі в першому виразі ми інтегруємо\(f(x,y)\) з\(x\) постійним, і межі інтеграції буття\(g_1(x)\) і\(g_2(x)\). У внутрішньому інтегралі у другому виразі ми інтегруємо\(f(x,y)\) з\(y\) постійним, а межі інтеграції є\(h_1(x)\) і\(h_2(x)\).

Приклад\(\PageIndex{2}\): Evaluating an Iterated Integral over a Type I Region

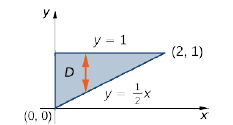
Оцініть інтеграл\(\displaystyle \iint \limits _D x^2 e^{xy} \,dA\), де\(D\) показано на малюнку\(\PageIndex{5}\).

Рішення

Спочатку побудуйте область як область типу I (рис.\(\PageIndex{5}\)). Ось\(D = \big\{(x,y) \,|\, 0 \leq x \leq 2, \space \frac{1}{2} x \leq y \leq 1\big\}\). Тоді у нас є

\[\iint \limits _D x^2e^{xy} \,dA = \int_{x=0}^{x=2} \int_{y=1/2x}^{y=1} x^2e^{xy}\,dy\,dx. \nonumber \]

Малюнок\(\PageIndex{5}\): Ми можемо виразити регіон\(D\) як область типу I і інтегрувати від\(y = \frac{1}{2} x\) до\(y = 1\) між лініями\(x = 0\) і\(x = 2\).

Тому у нас є

\[\begin{align*} \int_{x=0}^{x=2}\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\,dx &= \int_{x=0}^{x=2}\left[\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\right] dx & &\text{Iterated integral for a Type I region.}\\[5pt] &=\int_{x=0}^{x=2} \left.\left[ x^2 \frac{e^{xy}}{x} \right] \right|_{y=1/2x}^{y=1}\,dx & & \text{Integrate with respect to $y$}\\[5pt] &= \int_{x=0}^{x=2} \left[xe^x - xe^{x^2/2}\right]dx & & \text{Integrate with respect to $x$} \\[5pt] &=\left[xe^x - e^x - e^{\frac{1}{2}x^2} \right] \Big|_{x=0}^{x=2} = 2. \end{align*}\]

У прикладі\(\PageIndex{2}\) ми могли б подивитися на регіон по-іншому, наприклад\(D = \big\{(x,y)\,|\,0 \leq y \leq 1, \space 0 \leq x \leq 2y\big\}\) (Рис.\(\PageIndex{6}\)).

Малюнок\(\PageIndex{6}\).

Це область типу II, і інтеграл буде виглядати так

\[\iint \limits _D x^2e^{xy}\,dA = \int_{y=0}^{y=1} \int_{x=0}^{x=2y} x^2 e^{xy}\,dx \space dy. \nonumber \]

Однак, якщо ми інтегруємо спочатку щодо\(x\) цього інтеграла, це довго обчислювати, оскільки ми повинні використовувати інтеграцію частинами двічі.

Приклад\(\PageIndex{3}\): Evaluating an Iterated Integral over a Type II Region

Оцініть інтеграл

\[\iint \limits _D (3x^2 + y^2) \,dA \nonumber \]

де\(D = \big\{(x,y)\,| \, -2 \leq y \leq 3, \space y^2 - 3 \leq x \leq y + 3\big\}\).

Рішення

Зверніть увагу, що\(D\) можна розглядати як область типу I або типу II, як показано на малюнку\(\PageIndex{7}\). Однак у цьому випадку описати\(D\) як тип I складніше, ніж описати його як тип II. Тому ми використовуємо\(D\) як регіон типу II для інтеграції.

Малюнок\(\PageIndex{7}\): Регіон\(D\) у цьому прикладі може бути або (a) Тип I або (b) Тип II.

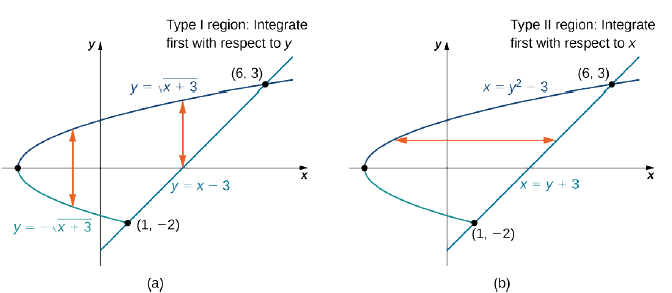
Вибираючи такий порядок інтеграції, ми маємо

\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[5pt] &=\int_{y=-2}^{y=3} \left. (x^3 + xy^2) \right|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[5pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\ &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[5pt] &= \left[ 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right]_{-2}^3 \\ &=\frac{2375}{7}. \end{align*}\]

Вправа\(\PageIndex{2}\)

Намалюйте область\(D\) та оцініть ітераційний інтеграл,\[\iint \limits _D xy \space dy \space dx \nonumber \] де\(D\) область обмежена кривими\(y = \cos \space x\) та\(y = \sin \space x\) в інтервалі\([-3\pi/4, \space \pi/4]\).

Підказка

Експрес\(D\) як регіон типу I, і інтегрувати по відношенню до\(y\) першого.

Відповідь

\(\frac{\pi}{4}\)

Нагадаємо з подвійних інтегралів над прямокутними областями властивості подвійних інтегралів. Як ми бачили з прикладів тут, всі ці властивості також дійсні для функції, визначеної на непрямокутній обмеженій області на площині. Зокрема, у власності 3 зазначено:

Якщо\(R = S \cup T\) і\(S \cap T = 0\) крім їх кордонів, то

\[\iint \limits _R f(x,y)\,dA = \iint\limits _S f(x,y)\,dA + \iint\limits _T f(x,y) \,dA. \nonumber \]

Аналогічно, ми маємо таку властивість подвійних інтегралів над непрямокутною обмеженою областю на площині.

Теорема: Розкладання областей на менші регіони

Припустимо, область\(D\) може бути виражена як\(D = D_1 \cup D_2\) де\(D_1\) і\(D_2\) не перекриватися хіба що на їх кордоні. Тоді

\[\iint \limits _D f(x,y) \,dA = \iint \limits _{D_1} f(x,y) \,dA + \iint \limits _{D_2} f(x,y) \,dA. \nonumber \]

Ця теорема особливо корисна для непрямокутних областей, оскільки дозволяє розділити область на об'єднання областей типу I та II типу. Тоді ми можемо обчислити подвійний інтеграл на кожному шматочку зручним способом, як у наступному прикладі.

Приклад\(\PageIndex{4}\): Decomposing Regions

Висловіть область,\(D\) показану на малюнку,\(\PageIndex{8}\) як об'єднання регіонів типу I або типу II, і оцініть інтеграл

\[\iint \limits _D (2x + 5y)\,dA. \nonumber \]

Малюнок\(\PageIndex{8}\): Ця область може бути розкладена на об'єднання трьох областей типу I або типу II.

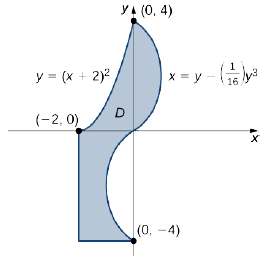
Рішення

Регіон\(D\) непросто розкласти на якийсь один тип; насправді це поєднання різних типів. Таким чином, ми можемо написати це як об'єднання трьох регіонів\(D_1\)\(D_2\), і\(D_3\) де\(D_1 = \big\{(x,y)\,| \, -2 \leq x \leq 0, \space 0 \leq y \leq (x + 2)^2 \big\}\),\(D_2 = \big\{(x,y)\,| \, 0 \leq y \leq 4, \space 0 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\), і\(D_3 = \big\{(x,y)\,| \, -4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\). Ці регіони більш наочно проілюстровані на малюнку\(\PageIndex{9}\).

Малюнок\(\PageIndex{9}\): Розбиття регіону на три субрегіони полегшує налаштування інтеграції.

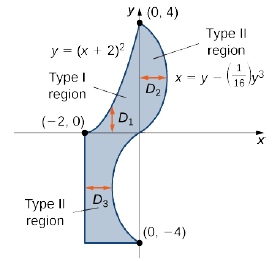
\(D_1\)Ось тип I\(D_2\) і і\(D_3\) обидва типу II. Отже,

\[\begin{align*} \iint\limits_D (2x + 5y)\,dA &= \iint\limits_{D_1} (2x + 5y)\,dA + \iint\limits_{D_2} (2x + 5y)\,dA + \iint\limits_{D_3} (2x + 5y)\,dA \\ &= \int_{x=-2}^{x=0} \int_{y=0}^{y=(x+2)^2} (2x + 5y) \,dy \space dx + \int_{y=0}^{y=4} \int_{x=0}^{x=y-(1/16)y^3} (2 + 5y)\,dx \space dy + \int_{y=-4}^{y=0} \int_{x=-2}^{x=y-(1/16)y^3} (2x + 5y)\,dx \space dy \\ &= \int_{x=-2}^{x=0} \left[\frac{1}{2}(2 + x)^2 (20 + 24x + 5x^2)\right]\,dx + \int_{y=0}^{y=4} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 \right]\,dy +\int_{y=-4}^{y=0} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 + 10y - 4\right] \,dy\\ &= \frac{40}{3} + \frac{1664}{35} - \frac{1696}{35} = \frac{1304}{105}.\end{align*}\]

Тепер ми могли б повторити цей приклад, використовуючи об'єднання двох областей типу II (див. Checkpoint).

Вправа\(\PageIndex{3}\)

Розглянемо область, обмежену кривими\(y = \ln x\) і\(y = e^x\) в інтервалі\([1,2]\). Розкладіть область на менші області типу II.

Підказка

Намалюйте область та розділіть її на три області, щоб налаштувати її.

Відповідь

\[\big\{(x,y)\,| \, 0 \leq y \leq 1, \space 1 \leq x \leq e^y \big\} \cup \big\{(x,y)\,| \, 1 \leq y \leq e, \space 1 \leq x \leq 2 \big\} \cup \big\{(x,y)\,| \, e \leq y \leq e^2, \space \ln y \leq x \leq 2 \big\} \nonumber \]

Вправа\(\PageIndex{4}\)

Повторити приклад з\(\PageIndex{4}\) використанням об'єднання двох областей типу II.

Підказка

\[\big\{(x,y)\,| \, 0 \leq y \leq 4, \space 2 + \sqrt{y} \leq x \leq \big(y - \frac{1}{16}y^3\big) \big\} \cup \big\{(x,y)\,| \, - 4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16}y^{13}\big) \big\} \nonumber \]

Відповідь

Те ж саме, що і в показаному прикладі.

Зміна порядку інтеграції

Як ми вже бачили, коли ми оцінюємо ітераційний інтеграл, іноді один порядок інтеграції призводить до обчислення, який значно простіший, ніж інший порядок інтеграції. Іноді порядок інтеграції не має значення, але важливо навчитися розпізнавати, коли зміна порядку спростить нашу роботу.

Приклад\(\PageIndex{5}\): Changing the Order of Integration

Зворотний порядок інтеграції в ітераційний інтеграл

\[\int_{x=0}^{x=\sqrt{2}} \int_{y=0}^{y=2-x^2} xe^{x^2} \,dy \space dx. \nonumber \]

Потім оцініть новий ітераційний інтеграл.

Рішення

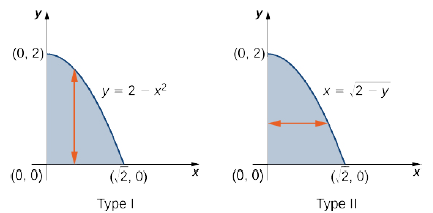
Представлений регіон має тип I. Щоб змінити порядок інтеграції, ми повинні спочатку виразити регіон як тип II. Зверніться до рис\(\PageIndex{10}\).

Малюнок\(\PageIndex{10}\): Перетворення області з типу I в тип II.

З меж інтеграції ми бачимо, що регіон обмежений вище\(y = 2 - x^2\) і нижче,\(y = 0\) де\(x\) знаходиться в інтервалі\([0, \sqrt{2}]\). Змінюючи порядок, ми маємо область, обмежену ліворуч\(x = 0\) і праворуч тим,\(x = \sqrt{2 - y}\) де\(y\) знаходиться в інтервалі\([0, 2]\). \(y = 2 - x^2\)Вирішили з точки зору\(x\) отримання\(x = \sqrt{2 - y}\).

Звідси

\[\begin{align*} \int_0^{\sqrt{2}} \int_0^{2-x^2} xe^{x^2} dy \space dx &= \int_0^2 \int_0^{\sqrt{2-y}} xe^{x^2}\,dx \space dy &\text{Reverse the order of integration then use substitution.} \\[4pt] &= \int_0^2 \left[\left.\frac{1}{2}e^{x^2}\right|_0^{\sqrt{2-y}}\right] dy = \int_0^2\frac{1}{2}(e^{2-y} - 1)\,dy \\[4pt] &= -\left.\frac{1}{2}(e^{2-y} + y)\right|_0^2 = \frac{1}{2}(e^2 - 3). \end{align*}\]

Приклад\(\PageIndex{6}\): Evaluating an Iterated Integral by Reversing the Order of Integration

Розглянемо ітераційний інтеграл

\[\iint\limits_R f(x,y)\,dx \space dy \nonumber \]

де\(z = f(x,y) = x - 2y\) над трикутної області\(R\), яка має сторони на\(x = 0, \space y = 0\), і лінії\(x + y = 1\). Намалюйте область, а потім оцініть ітераційний інтеграл за

1. інтегруючи спочатку стосовно,\(y\) а потім
2. інтегруючи спочатку по відношенню до\(x\).

Рішення

Ескіз області відображається на малюнку\(\PageIndex{11}\).

Малюнок\(\PageIndex{11}\): Трикутна область\(R\) для інтеграції двома способами.

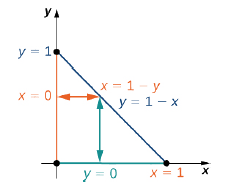
Ми можемо завершити цю інтеграцію двома різними способами.

a Один із способів подивитися на це - спочатку інтегрувати\(y\) від\(y = 0\) до\(y = 1 - x\) вертикально, а потім інтегрувати\(x\) від\(x = 0\) до\(x = 1\):

\[\begin{align*} \iint\limits_R f(x,y) \,dx \space dy &= \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} (x - 2y) \,dy \space dx = \int_{x=0}^{x=1}\left(xy - 2y^2\right)\Big|_{y=0}^{y=1-x} dx \\[4pt] &=\int_{x=0}^{x=1} \left[ x(1 - x) - (1 - x)^2\right] \,dx = \int_{x=0}^{x=1} [ -1 + 3x - 2x^2] dx = \left[ -x + \frac{3}{2}x^2 - \frac{2}{3} x^3 \right]\Big|_{x=0}^{x=1} = -\frac{1}{6}. \end{align*}\]

б Інший спосіб вирішити цю проблему полягає в тому, щоб спочатку інтегрувати\(x\) від\(x = 0\) до\(x = 1 - y\) горизонтально, а потім інтегрувати\(y\) від\(y = 0\) до\(y = 1\):

\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[4pt] &=\int_{y=-2}^{y=3} (x^3 + xy^2) \Big|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[4pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\[4pt] &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[4pt] &= \left( 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right)\Big|_{-2}^3 \\[4pt] &=\frac{2375}{7}. \end{align*}\]

Вправа\(\PageIndex{5}\)

Оцініть ітераційний інтеграл\(\displaystyle \iint\limits_D (x^2 + y^2)\,dA\) по області\(D\) в першому квадранті між функціями\(y = 2x\) і\(y = x^2\). Оцініть ітераційний інтеграл, інтегруючи спочатку по відношенню до,\(y\) а потім інтегруючи спочатку з resect to\(x\).

Підказка

Намалюйте область і дотримуйтесь Прикладу\(\PageIndex{6}\).

Відповідь

\(\frac{216}{35}\)

Обчислення обсягів, площ та середніх значень

Ми можемо використовувати подвійні інтеграли над загальними регіонами для обчислення обсягів, площ та середніх значень. Методи такі ж, як у подвійних інтегралах над прямокутними областями, але без обмеження прямокутної області ми можемо вирішувати більш широкий спектр проблем.

Приклад\(\PageIndex{7}\): Finding the Volume of a Tetrahedron

Знайти об'єм твердого тіла, обмеженого площинами\(x = 0, \space y = 0, \space z = 0\), і\(2x + 3y + z = 6\).

Рішення

Тверда речовина являє собою тетраедр з підставою на\(xy\) -площині і висотою\(z = 6 - 2x - 3y\). Підстава - область,\(D\) обмежена лініями\(x = 0\),\(y = 0\) і\(2x + 3y = 6\) де\(z = 0\) (рис.\(\PageIndex{12}\)). Зауважте, що ми можемо розглядати регіон\(D\) як тип I або як тип II, і ми можемо інтегруватися обома способами.

Малюнок\(\PageIndex{12}\): Тетраедр, що складається з трьох координатних площин і площини\(z = 6 - 2x - 3y\), з основою,\(x = 0, \space y = 0\) пов'язаною, і\(2x + 3y = 6\).

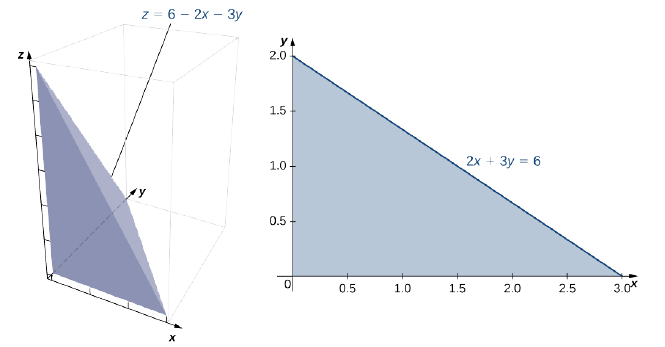
По-перше, розгляньте\(D\) як регіон типу I, а отже\(D = \big\{(x,y)\,| \, 0 \leq x \leq 3, \space 0 \leq y \leq 2 - \frac{2}{3} x \big\}\).

Тому обсяг становить

\[\begin{align*} V &= \int_{x=0}^{x=3} \int_{y=0}^{y=2-(2x/3)} (6 - 2x - 3y) \,dy \space dx = \int_{x=0}^{x=3} \left[ \left.\left( 6y - 2xy - \frac{3}{2}y^2\right)\right|_{y=0}^{y=2-(2x/3)} \right] \,dx\\[4pt] &= \int_{x=0}^{x=3} \left[\frac{2}{3} (x - 3)^2 \right] \,dx = 6. \end{align*}\]

Тепер розглянемо\(D\) як регіон типу II, так\(D = \big\{(x,y)\,| \, 0 \leq y \leq 2, \space 0 \leq x \leq 3 - \frac{3}{2}y \big\}\). У цьому розрахунку обсяг дорівнює

\[\begin{align*} V &= \int_{y=0}^{y=2} \int_{x=0}^{x=3-(3y/2)} (6 - 2x - 3y)\,dx \space dy = \int_{y=0}^{y=2} \left[(6x - x^2 - 3xy)\Big|_{x=0}^{x=3-(3y/2)} \right] \,dy \\[4pt] &= \int_{y=0}^{y=2} \left[\frac{9}{4}(y - 2)^2 \right] \,dy = 6.\end{align*}\]

Тому обсяг становить 6 кубічних одиниць.

Вправа\(\PageIndex{6}\)

Знайдіть об'єм твердого тіла, обмеженого вище\(f(x,y) = 10 - 2x + y\) над областю, укладеною кривими\(y = 0\) і\(y = e^x\) де\(x\) знаходиться в інтервалі\([0,1]\).

Підказка

Намалюйте область і опишіть її як тип I.

Відповідь

\(\frac{e^2}{4} + 10e - \frac{49}{4}\)кубічні одиниці

Знайти площу прямокутної області нескладно, але знайти площу непрямокутної області не так-то просто. Як ми бачили, ми можемо використовувати подвійні інтеграли, щоб знайти прямокутну область. Власне кажучи, це дуже зручно для знаходження площі загальної непрямокутної області, як зазначено в наступному визначенні.

Визначення: Подвійні інтеграли

Площа площини обмеженої області\(D\) визначається як подвійний інтеграл

\[\iint\limits_D 1\,dA. \nonumber \]

Ми вже бачили, як знайти області з точки зору єдиної інтеграції. Тут ми бачимо ще один спосіб пошуку областей за допомогою подвійних інтегралів, що може бути дуже корисним, як ми побачимо в наступних розділах цієї глави.

Приклад\(\PageIndex{8}\): Finding the Area of a Region

Знайдіть площу області, обмеженої нижче кривою\(y = x^2\) і вище лінією\(y = 2x\) в першому квадранті (рис.\(\PageIndex{13}\)).

Малюнок\(\PageIndex{13}\): Регіон, обмежений\(y = x^2\) і\(y = 2x\).

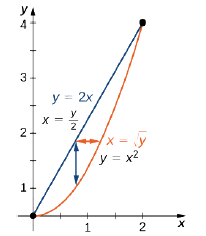
Рішення

Нам просто потрібно інтегрувати постійну функцію\(f(x,y) = 1\) по регіону. Таким чином, площа\(A\) обмеженої області становить\(\displaystyle \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} dy \space dx \space \text{or} \space \int_{y=0}^{y=4} \int_{x=y/2}^{x=\sqrt{y}} dx \space dy:\)

\[\begin{align*} A &= \iint\limits_D 1\,dx \space dy \\[4pt] &= \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} 1\,dy \space dx \\[4pt] &= \int_{x=0}^{x=2} \left(y\Big|_{y=x^2}^{y=2x} \right) \,dx \\[4pt] &= \int_{x=0}^{x=2} (2x - x^2)\,dx \\[4pt] &= \left(x^2 - \frac{x^3}{3}\right) \Big|_0^2 = \frac{4}{3}. \end{align*}\]

Вправа\(\PageIndex{7}\)

Знайдіть площу області, обмеженої вище кривою\(y = x^3\) і знизу\(y = 0\) за інтервалом\([0,3]\).

Підказка

Намалюйте регіон.

Відповідь

\(\frac{81}{4}\)квадратні одиниці

Ми також можемо використовувати подвійний інтеграл, щоб знайти середнє значення функції над загальною областю. Визначення є прямим продовженням більш ранньої формули.

Визначення: Середнє значення функції

Якщо\(f (x,y)\) інтегрується над плоскою областю\(D\) з додатною площею\(A(D)\), то середнє значення функції дорівнює

\[f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA. \nonumber \]

Зверніть увагу, що площа є\(\displaystyle A(D) = \iint\limits_D 1\,dA\).

Приклад\(\PageIndex{9}\): Finding an Average Value

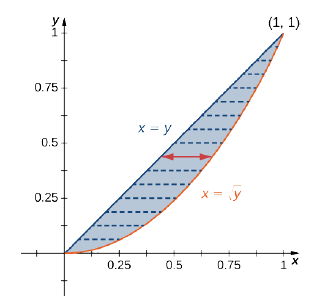
Знайти середнє значення функції\(f(x,y) = 7xy^2\) на області, обмеженій лінією\(x = y\) і кривою\(x = \sqrt{y}\) (рис.\(\PageIndex{14}\)).

Малюнок\(\PageIndex{14}\): Регіон, обмежений\(x = y\) і\(x = \sqrt{y}\).

Рішення

Спочатку знайдіть область,\(A(D)\) де область\(D\) задана фігурою. У нас є

\[A(D) = \iint\limits_D 1\,dA = \int_{y=0}^{y=1} \int_{x=y}^{x=\sqrt{y}} 1\,dx \space dy = \int_{y=0}^{y=1} \left[x \Big|_{x=y}^{x=\sqrt{y}} \right] \,dy = \int_{y=0}^{y=1} (\sqrt{y} - y) \,dy = \frac{2}{3}\left. y^{2/3} - \frac{y^2}{2} \right|_0^1 = \frac{1}{6} \nonumber \]

Тоді середнє значення даної функції над цією областю дорівнює

\[\begin{align*} f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA = \frac{1}{A(D)} \int_{y=0}^{y=1}\int_{x=y}^{x=\sqrt{y}} 7xy^2 \,dx \space dy = \frac{1}{1/6} \int_{y=0}^{y=1} \left[ \left. \frac{7}{2} x^2y^2 \right|_{x=y}^{x=\sqrt{y}} \right] \,dy \\ = 6 \int_{y=0}^{y=1} \left[ \frac{7}{2} y^2 (y - y^2)\right] \,dy = 6\int_{y=0}^{y=1} \left[ \frac{7}{2} (y^3 -y^4) \right] \,dy = \frac{42}{2} \left. \left( \frac{y^4}{4} - \frac{y^5}{5}\right) \right|_0^1 = \frac{42}{40} = \frac{21}{20}. \end{align*}\]

Вправа\(\PageIndex{8}\)

Знайти середнє значення функції\(f(x,y) = xy\) над трикутником з вершинами\((0,0), \space (1,0)\) і\((1,3)\).

Підказка

Висловіть приєднання лінії\((0,0)\) і\((1,3)\) як функцію\(y = g(x)\).

Відповідь

\(\frac{3}{4}\)

Неправильні подвійні інтеграли

Неправильний подвійний інтеграл є\(\displaystyle \iint\limits_D f \,dA\) інтегралом, де або\(D\) є необмеженою областю, або\(f\) є необмеженою функцією. Наприклад,\(D = \big\{(x,y) \,|\,|x - y| \geq 2\big\}\) є необмеженою областю, а функція\(f(x,y) = 1/(1 - x^2 - 2y^2)\) над еліпсом\(x^2 + 3y^2 \geq 1\) є необмеженою функцією. Отже, обидва наступні інтеграли є неправильними інтегралами:

1. \[\iint\limits_D xy \space dA \space \text{where} \space D = \big\{(x,y)| | \, x - y| \geq 2 \big\}; \nonumber \]
2. \[\iint\limits_D \frac{1}{1 - x^2 -2y^2}\,dA \space \text{where} \space D = \big\{(x,y)| \, x^2 + 3y^2 \leq 1 \big\}. \nonumber \]

У цьому розділі ми хотіли б розібратися з неправильними інтегралами функцій над прямокутниками або простими областями, такими, що f має лише скінченно багато розривів. Не всі такі неправильні інтеграли можуть бути оцінені; однак форма теореми Фубіні застосовується для деяких типів неправильних інтегралів.

Теорема: Теорема Фубіні для неправильних інтегралів

Якщо\(D\) є обмеженим прямокутником або простою областю в площині, визначеної

\(\big\{(x,y)\,: a \leq x \leq b, \space g(x) \leq y \leq h(x) \big\}\)а також

\(\big\{(x,y)\,: c \leq y \leq d, \space j(y) \leq x \leq k(y)\big\}\)і\(f\) є ненегативною функцією на\(D\) з скінченно багатьма розривами в інтер'єрі\(D\) тоді

\[\iint\limits_D f \space dA = \int_{x=a}^{x=b} \int_{y=g(x)}^{y=h(x)} f(x,y) \,dy \space dx = \int_{y=c}^{y=d} \int_{x=j(y)}^{x=k(y)} f(x,y) \,dx \space dy \nonumber \]

Дуже важливо зазначити, що ми вимагали, щоб функція була\(D\) невід'ємною для роботи теореми. Розглянемо лише той випадок, коли функція має скінченно багато розривів всередині\(D\).

Приклад\(\PageIndex{10}\): Evaluating a Double Improper Integral

Розглянемо функцію\(f(x,y) = \frac{e^y}{y}\) над регіоном\(D = \big\{(x,y)\,: 0 \leq x \leq 1, \space x \leq y \leq \sqrt{x}\big\}.\)

Зверніть увагу, що функція невід'ємна і безперервна у всіх точках\(D\) крім\((0,0)\). Використовуйте теорему Фубіні для оцінки неправильного інтеграла.

Рішення

Спочатку намічаємо область\(D\) (рис.\(\PageIndex{15}\)); потім виражаємо її іншим способом.

Малюнок\(\PageIndex{15}\): Функція\(f\) є безперервною у всіх точках області,\(D\) крім\((0,0)\).

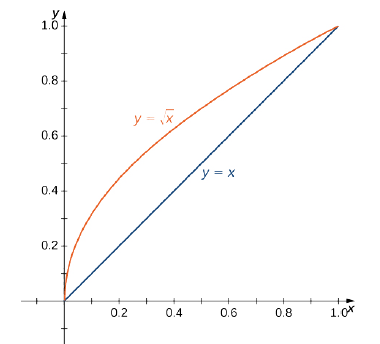
Інший спосіб висловити той\(D\) самий регіон:

\[D = \big\{(x,y)\,: \, 0 \leq y \leq 1, \space y^2 \leq x \leq y \big\}. \nonumber \]

Таким чином, ми можемо використовувати теорему Фубіні для неправильних інтегралів і оцінити інтеграл як

\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy. \nonumber \]

Тому у нас є

\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy = \int_{y=0}^{y=1} \left. \frac{e^y}{y}x\right|_{x=y^2}^{x=y} \,dy = \int_{y=0}^{y=1} \frac{e^y}{y} (y - y^2) \,dy = \int_0^1 (e^y - ye^y)\,dy = e - 2. \nonumber \]

Як уже згадувалося раніше, ми також маємо неправильний інтеграл, якщо регіон інтеграції необмежений. Припустимо тепер,\(f\) що функція безперервна в необмеженому прямокутнику\(R\).

Теорема: Неправильні інтеграли на необмеженій області

Якщо\(R\) необмежений прямокутник\(R = \big\{(x,y)\,: \, a \leq x \leq \infty, \space c \leq y \leq \infty \big\}\), наприклад, тоді, коли межа існує, ми маємо

\[\iint\limits_R f(x,y) \,dA = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_a^b \left(\int_c^d f (x,y) \,dy \right) dx = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_c^d \left(\int_a^b f(x,y) \,dx \right) dy. \nonumber \]

Наступний приклад показує, як ця теорема може бути використана в певних випадках неправильних інтегралів.

Приклад\(\PageIndex{11}\)

Оцініть інтеграл\(\iint\limits_R xye^{-x^2-y^2}\,dA\), де\(R\) знаходиться перший квадрант площини.

Рішення

Область\(R\) - це перший квадрант площини, який необмежений. Так

\[\begin{align*} \iint\limits_R xye^{-x^2-y^2} \,dA &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{x=0}^{x=b} \left(\int_{y=0}^{y=d} xye^{-x^2-y^2} dy\right) \,dx \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{y=0}^{x=b} xye^{-x^2-y^2} \,dy \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \frac{1}{4} \left(1 - e^{-b^2}\right) \left( 1 - e^{-d^2}\right) = \frac{1}{4} \end{align*}\]

Таким чином,

\[\iint\limits_R xye^{-x^2-y^2}\,dA \nonumber \]

сходиться і значення є\(\frac{1}{4}\).

Вправа\(\PageIndex{9}\)

\[\iint\limits_D \frac{y}{\sqrt{1 - x^2 - y^2}}dA \nonumber \]де\(D = \big\{(x,y)\,: \, x \geq 0, \space y \geq 0, \space x^2 + y^2 \leq 1 \big\}\).

Підказка

Зверніть увагу, що інтеграл невід'ємний і переривчастий на\(x^2 + y^2 = 1\). Висловіть регіон\(D\) як\(D = \big\{(x,y)\,: \, 0 \leq x \leq 1, \space 0 \leq y \leq \sqrt{1 - x^2} \big\}\) і інтегруйте за допомогою методу підміни.

Відповідь

\(\frac{\pi}{4}\)

У деяких ситуаціях теорії ймовірностей ми можемо отримати уявлення про проблему, коли ми можемо використовувати подвійні інтеграли над загальними регіонами. Перш ніж ми перейдемо до прикладу з подвійним інтегралом, нам потрібно встановити кілька визначень і ознайомитися з деякими важливими властивостями.

Визначення: Функція щільності суглобів

Розглянемо пару суцільних випадкових величин\(X\) і\(Y\) таких, як дні народження двох людей або кількість сонячних і дощових днів у місяці. Функція\(f\) щільності суглоба\(X\) і\(Y\) задовольняє ймовірність того, що\((X,Y)\) лежить в певній області\(D\):

\[P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA. \nonumber \]

Оскільки ймовірності ніколи не можуть бути від'ємними і повинні лежати між 0 і 1, функція щільності суглоба задовольняє такі нерівності та рівняння:

\[f(x,y) \geq 0 \space \text{and} \space \iint\limits_R f(x,y) \,dA = 1. \nonumber \]

Визначення: Незалежні випадкові величини

Змінні\(X\) і\(Y\), як кажуть, є незалежними випадковими величинами, якщо їх спільна функція щільності є добутком їх індивідуальних функцій щільності:

\[f(x,y) = f_1(x) f_2(y). \nonumber \]

Приклад\(\PageIndex{12}\): Application to Probability

У ресторані Сіднея клієнти повинні чекати в середньому 15 хвилин за столом. З того часу, як вони сидять, поки вони не закінчать їжу, потрібно в середньому додаткові 40 хвилин. Яка ймовірність того, що клієнт проводить в закусочній менше півтори години, припускаючи, що очікування столу і завершення трапези - це самостійні заходи?

Рішення

Час очікування математично моделюється функціями експоненціальної щільності,\(m\) причому середній час очікування, як

\[f(t) = \begin{cases} 0, & \text{if}\; t<0 \\ \dfrac{1}{m}e^{-t/m}, & \text{if} \; t\geq 0.\end{cases} \nonumber \]

якщо\(X\) і\(Y\) є випадковими величинами для «очікування столу» та «завершення прийому їжі», то функції щільності ймовірності, відповідно,

\[f_1(x) = \begin{cases} 0, & \text{if}\; x<0. \\ \dfrac{1}{15} e^{-x/15}, & \text{if} \; x\geq 0. \end{cases} \quad \text{and} \quad f_2(y) = \begin{cases} 0, & \text{if}\; y<0 \\ \dfrac{1}{40} e^{-y/40}, & \text{if}\; y\geq 0. \end{cases} \nonumber \]

Зрозуміло, що події є незалежними, і, отже, функція щільності суглоба є продуктом окремих функцій

\[f(x,y) = f_1(x)f_2(y) = \begin{cases} 0, & \text{if} \; x<0 \; \text{or} \; y<0, \\ \dfrac{1}{600} e^{-x/15}, & \text{if} \; x,y\geq 0 \end{cases} \nonumber \]

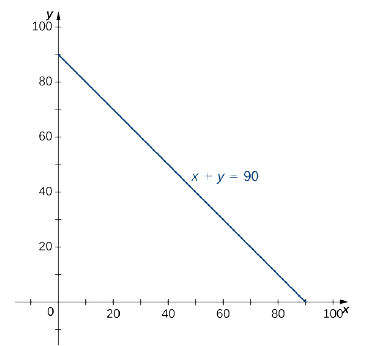
Ми хочемо знайти ймовірність того, що\(X + Y\) комбінований час менше 90 хвилин. З точки зору геометрії це означає, що область\(D\) знаходиться в першому квадранті, обмеженому лінією\(x + y = 90\) (рис.\(\PageIndex{16}\)).

Рисунок\(\PageIndex{16}\): Область інтеграції для спільної функції щільності ймовірності.

Значить, ймовірність того, що\((X,Y)\) знаходиться в регіоні,\(D\) є

\[P(X + Y \leq 90) = P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA = \iint\limits_D \frac{1}{600}e^{-x/15} e^{-y/40} \,dA. \nonumber \]

Оскільки\(x + y = 90\) це те ж саме\(y = 90 - x\), що у нас є область типу I, тому

\[\begin{align*} D &= \big\{(x,y)\,|\,0 \leq x \leq 90, \space 0 \leq y \leq 90 - x\big\}, \\[6pt] P(X + Y \leq 90) &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(/15}e^{-y/40}dx \space dy = \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x}e^{-x/15}e^{-y/40} dx \space dy \\[6pt] &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(x/15+y/40)}dx \space dy = 0.8328 \end{align*}\]

Таким чином, є\(83.2\%\) ймовірність того, що клієнт проводить в ресторані менше півтори години.

Ще одним важливим додатком ймовірності, яке може включати неправильні подвійні інтеграли, є обчислення очікуваних значень. Спочатку ми визначаємо це поняття, а потім покажемо приклад розрахунку.

Визначення: Очікувані значення

У теорії ймовірностей позначимо очікувані значення\(E(X)\) і\(E(Y)\) відповідно, як найбільш ймовірні результати подій. Очікувані значення\(E(X)\) і\(E(Y)\) задаються

\[E(X) = \iint\limits_S x\,f(x,y) \,dA \space and \space E(Y) = \iint\limits_S y\,f (x,y) \,dA, \nonumber \]

де\(S\) - простір вибірки випадкових величин\(X\) і\(Y\).

Приклад\(\PageIndex{13}\): Finding Expected Value

Знайдіть очікуваний час подій «очікування столу» та «завершення їжі» у прикладі\(\PageIndex{12}\).

Рішення

Використовуючи перший квадрант прямокутної координатної площини як простір вибірки, ми маємо неправильні інтеграли для\(E(X)\) і\(E(Y)\). Очікуваний час для столу -

\ [\ почати {вирівнювати*} E (X) &=\ iint\ limits_s х\ розрив {1} {600} e^ {-x/15} e^ {-y/40}\, Да\\ [6пт]
&=\ frac {1} {600}\ int_ {x = 0} ^ {x=\ infty}\ int_ {y=0}\ infty} x^ {-x/15} e^ {-y/40} да\\ [6pt]
&=\ розрив {1} {600}\ lim_ {(a, b)\ стрілка вправо (\ infty,\ infty)}\ int_ {x=0} ^ {x = a}\ int_ {y=0} ^ {y=b} xe^ {-x/15} e^ {-y/40} dx\ простір dy\\ [6pt]
&=\ розрив {1} {600}\ ліворуч (\ lim_ {a\ праворуч\ infty}\ int_ {x = 0} ^ {x = a} xe^ {-x/15} дх\ вправо)\ ліворуч (\ lim_ {b\ праворуч\ infty} _ {y=0} ^ {y=b} e^ {-y/40} ди\ праворуч)\\ [6pt]
&=\ розриву {1} {600}\ ліворуч (\ ліворуч. (\ lim_ {a\ праворуч\ infty} (-15e^ {-x/15} (x + 15)))\ праворуч |_ {x = 0} ^ {x = a}\ праворуч)\ ліворуч (\ ліворуч. (\ lim_ {b\ праворуч\ infty} (-40e^ {-y/40}))\ праворуч | _ {y = 0} ^ {y=b}\ праворуч)\\ [6pt]
&=\ frac {1} {600}\ ліворуч (\ lim_ {a\ стрілка вправо\ infty} (-15e^ {-a/15} (x + 15) + 25)\ праворуч)\ ліворуч (\ lim_ {b\ rightarrow\ infty} (- 40e^ {-b/40} + 40)\ праворуч)\\ [6pt]
&=\ гідророзриву {1} {600} (225) (40) = 15. \ end {вирівнювати*}\]

Подібний розрахунок показує, що\(E(Y) = 40\). Це означає, що очікувані значення двох випадкових подій - це середній час очікування та середній час обіду відповідно.

Вправа\(\PageIndex{10}\)

Функція щільності з'єднання для двох випадкових величин\(X\) і\(Y\) задається

\[f(x,y) =\begin{cases}\frac{1}{600} (x^2 + y^2),\; & \text{if} \; \leq x \leq 15, \; 0 \leq y \leq 10 \\ 0, & \text{otherwise} \end{cases} \nonumber \]

Знайдіть ймовірність,\(X\) що не більше 10 і\(Y\) становить не менше 5.

Підказка

Обчислити ймовірність

\[P(X \leq 10, \space Y \geq 5) = \int_{x=-\infty}^{10} \int_{y=5}^{y=10} \frac{1}{6000} (x^2 + y^2) dy \space dx. \nonumber \]

Відповідь

\(\frac{55}{72} \approx 0.7638\)

Ключові поняття

• Загальна обмежена область\(D\) на площині - це область, яка може бути укладена всередині прямокутної області. Ми можемо використовувати цю ідею для визначення подвійного інтеграла над загальною обмеженою областю.
• Щоб оцінити ітераційний інтеграл функції над загальною непрямокутною областю, ми намалюємо область і виражаємо її як область типу I або як область типу II або як об'єднання декількох областей типу I або типу II, які перекриваються лише на їх межах.
• Ми можемо використовувати подвійні інтеграли для пошуку об'ємів, площ та середніх значень функції над загальними регіонами, подібно до обчислень над прямокутними областями.
• Теорему Фубіні для неправильних інтегралів можна використовувати для оцінки деяких типів неправильних інтегралів.

Ключові рівняння

• Ітераційний інтеграл над областю типу I

\[\iint\limits_D f(x,y) \,dA = \iint\limits_D f(x,y) \,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y) \,dy \right] dx \nonumber \]

• Ітераційний інтеграл над областю типу II

\[\iint\limits_D f(x,y) \,dA = \iint\limits_D (x,y) \,dx \space dy = \int_c^d \left[ \int_{h_1(y)}^{h_2(y)} f(x,y) \,dx \right] dy \nonumber \]

Глосарій

неправильний подвійний інтеграл

подвійний інтеграл над необмеженою областю або необмеженою функцією

Тип I

область\(D\) в площині\(xy\) - це тип I, якщо вона лежить між двома вертикальними лініями і графіками двох неперервних функцій\(g_1(x)\) і\(g_2(x)\)

Тип II

область\(D\) в\(xy\) -площині - тип II, якщо вона лежить між двома горизонтальними лініями та графіками двох неперервних функцій\(h_1(y)\) і\(h_2(h)\)