15.4: Потрійні інтеграли

Цілі навчання

• Визнайте, коли функція з трьох змінних інтегрується над прямокутним полем.
• Оцініть потрійний інтеграл, висловивши його як ітераційний інтеграл.
• Визнайте, коли функція з трьох змінних інтегрується над замкнутою та обмеженою областю.
• Спростити розрахунок, змінивши порядок інтеграції потрійного інтеграла.
• Обчисліть середнє значення функції трьох змінних.

Раніше ми розглядали подвійний інтеграл функції$f(x,y)$ двох змінних над прямокутною областю в площині. У цьому розділі ми визначаємо потрійний інтеграл функції$f(x,y,z)$ трьох змінних над прямокутною суцільною коробкою у просторі,$\mathbb{R}^3$. Пізніше в цьому розділі ми поширюємо визначення на більш загальні регіони в$\mathbb{R}^3$.

Інтегровані функції трьох змінних

Ми можемо визначити прямокутну коробку$B$ в$\mathbb{R}^3$ якості

$$B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber$$

Ми дотримуємося аналогічної процедури, що ми робили в раніше. Ділимо інтервал$[a,b]$ на$l$ підінтервали$[x_{i-1},x_i]$ рівної довжини$\Delta x$ з

$$\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber$$

$[c,d]$розділити інтервал на$m$ підінтервали$[y_{i-1}, y_i]$ рівної довжини$\Delta y$ з

$$\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber$$

і$[e,f]$ розділити інтервал на$n$ підінтервали$[z_{i-1},z_i]$ рівної довжини$\Delta z$ з

$$\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber$$

Потім прямокутний короб$B$ підрозділяється на$lmn$ підбокси:

$$B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber$$

як показано на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: Прямокутна коробка$\mathbb{R}^3$ розділена на підкоробки площинами, паралельними координатним площинам.

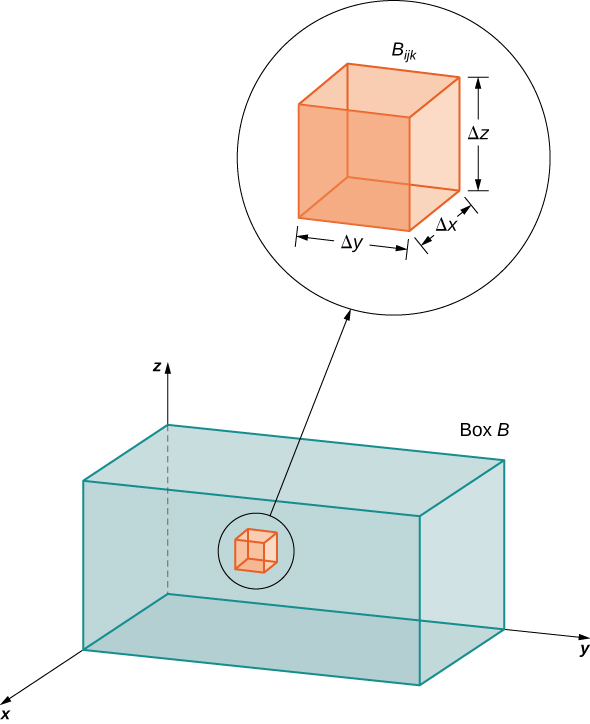
Для кожного$i, \, j,$ і$k$ розгляньте вибіркову точку$(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ в кожному підвікні$B_{ijk}$. Ми бачимо, що його обсяг є$\Delta V = \Delta x \Delta y \Delta z$. Сформуйте потрійну суму Рімана

$$\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber$$

Визначено потрійний інтеграл через межу потрійної суми Рімана, як це було зроблено для подвійного інтеграла через подвійну суму Рімана.

Визначення: Потрійний інтеграл

Потрійний інтеграл функції$f(x,y,z)$ над прямокутною коробкою$B$ визначається як

$$\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber$$ якщо цей ліміт існує.

Коли потрійний інтеграл існує$B$ на функції$f(x,y,z)$, як кажуть, інтегрується на$B$. Крім того, потрійний інтеграл існує$f(x,y,z)$, якщо він безперервний$B$. Тому ми будемо використовувати безперервні функції для наших прикладів. Однак безперервність є достатньою, але необов'язковою; іншими словами,$f$ обмежена$B$ і безперервна, за винятком, можливо, на межі$B$. Точка вибірки$(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ може бути будь-якою точкою прямокутної підкоробки,$B_{ijk}$ і всі властивості подвійного інтеграла застосовуються до потрійного інтеграла. Подібно до того, як подвійний інтеграл має багато практичних застосувань, потрійний інтеграл також має багато застосувань, про які ми обговорюємо в наступних розділах.

Тепер, коли ми розробили концепцію потрійного інтеграла, нам потрібно знати, як його обчислити. Так само, як і у випадку з подвійним інтегралом, ми можемо мати ітераційний потрійний інтеграл, і, отже, існує версія теореми Фубіні для потрійних інтегралів.

Теорема Фубіні для потрійних інтегралів

Якщо$f(x,y,z)$ суцільна на прямокутній коробці$B = [a,b] \times [c,d] \times [e,f]$, то

$$\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber$$

Цей інтеграл також дорівнює будь-якому з п'яти інших можливих порядків для ітераційного потрійного інтеграла.

Для$a, b, c, d, e$ і$f$ дійсних чисел ітераційний потрійний інтеграл може бути виражений у шести різних порядках:

$$\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber$$

Для прямокутної коробки порядок інтеграції не робить суттєвої різниці в рівні складності обчислень. Обчислено потрійні інтеграли, використовуючи теорему Фубіні, а не за допомогою визначення суми Рімана. Ми дотримуємося порядку інтеграції так само, як і для подвійних інтегралів (тобто зсередини назовні).

Приклад$\PageIndex{1}$: Evaluating a Triple Integral

Оцініть потрійний інтеграл $$\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber$$

Рішення

Порядок інтеграції задається в задачі, тому інтегруйте щодо$x$ спочатку, потім у, а потім$z$.

$$\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}$$

Приклад$\PageIndex{2}$: Evaluating a Triple Integral

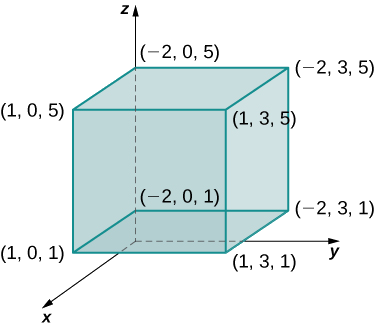
Оцініть потрійний інтеграл

$$\iiint_B x^2 yz \,dV \nonumber$$

де$B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\}$ як показано на рис$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Оцінка потрійного інтеграла над заданою прямокутною коробкою.

Рішення

Порядок не вказано, але ми можемо використовувати ітераційний інтеграл в будь-якому порядку без зміни рівня складності. Вибирайте, скажімо, інтегрувати$y$ спочатку, потім$x$, а потім$z$.

$$\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^3}{3} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{y}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = 162.\end{align*}$$

Тепер спробуйте інтегруватися в іншому порядку, щоб побачити, що ми отримаємо ту ж відповідь. Виберіть інтеграцію щодо$x$ спочатку, потім$z$, потім$y$

$$\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}$$

Вправа$\PageIndex{1}$

Оцініть потрійний інтеграл

$$\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber$$

де$B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}$.

Підказка

Виконайте дії в попередньому прикладі.

Відповідь

$$\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber$$

Потрійні інтеграли над загальною обмеженою областю

Тепер ми розширюємо визначення потрійного інтеграла, щоб обчислити потрійний інтеграл над більш загальною обмеженою областю$E$ в$\mathbb{R}^3$. Загальні обмежені регіони, які ми розглянемо, бувають трьох типів. По-перше, нехай$D$ бути обмежена область, яка є проекцією$E$ на$xy$ -plane. Припустимо, регіон$E$ в$\mathbb{R}^3$ має вигляд

$$E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Для двох функцій$z = u_1(x,y)$ і$u_2(x,y)$, таких, що$u_1(x,y) \leq u_2(x,y)$ для всіх$(x,y)$ в$D$ як показано на наступному малюнку.

Малюнок$\PageIndex{3}$: Ми можемо описати область$E$ як простір між$u_1(x,y)$ і$u_2(x,y)$ над$D$ проекцією$E$ на$xy$ -площину.

Потрійний інтеграл над загальним регіоном

Потрійний інтеграл неперервної функції$f(x,y,z)$ над загальною тривимірною областю

$$E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber$$

в$\mathbb{R}^3$, де$D$ проекція$E$ на$xy$ -площину, є

$$\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber$$

Аналогічно, ми можемо розглянути загальну обмежену область$D$ в$xy$ -площині і дві функції$y = u_1(x,z)$ і$y = u_2(x,z)$ такі, що$u_1(x,z) \leq u_2(x,z)$ для всіх$(x,z)$ в$D$. Тоді ми можемо описати тверду область$E$ в$\mathbb{R}^3$ якості

$$E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber$$ де$D$ проекція$E$ на$xy$ -площину і потрійний інтеграл

$$\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber$$

Нарешті, якщо$D$ є загальною обмеженою областю в$xy$ -площині і у нас є дві функції$x = u_1(y,z)$ і$x = u_2(y,z)$ такі, що$u_1(y,z) \leq u_2(y,z)$ для всіх$(y,z)$ в$D$, то тверда область$E$ в$\mathbb{R}^3$ може бути описана як

$$E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber$$ де$D$ проекція$E$ на$xy$ -площину і потрійний інтеграл

$$\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber$$

Зауважте, що область$D$ в будь-якій з площин може мати тип I або тип II, як описано раніше. Якщо$D$ в$xy$ -площині має тип I (рис.$\PageIndex{4}$), то

$$E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Малюнок$\PageIndex{4}$: Коробка,$E$ де проекція$D$ в$xy$ -площині має тип I.

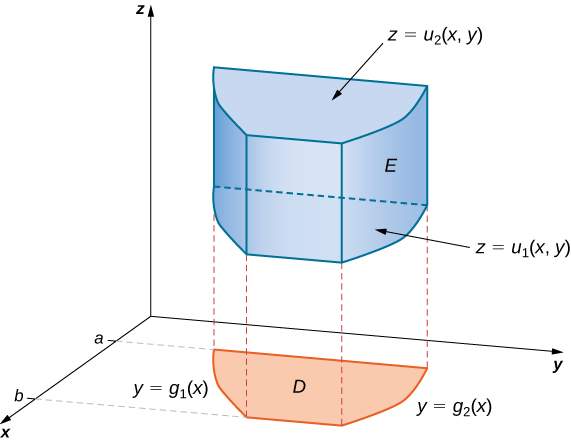
Тоді потрійний інтеграл стає

$$\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber$$

Якщо$D$ в$xy$ -площині має тип II (рис.$\PageIndex{5}$), то

$$E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber$$

Малюнок$\PageIndex{5}$: Коробка,$E$ де проекція$D$ в$xy$ -площині має тип II.

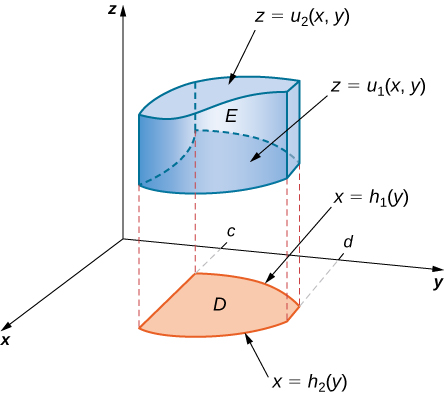
Тоді потрійний інтеграл стає

$$\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber$$

Приклад$\PageIndex{3A}$: Evaluating a Triple Integral over a General Bounded Region

Оцініть потрійний інтеграл функції$f(x,y,z) = 5x - 3y$ над твердим тетраедром, обмеженим площинами$x = 0, \, y = 0, \, z = 0$, і$x + y + z = 1$.

Рішення

$\PageIndex{6}$На малюнку показаний суцільний тетраедр$E$ і його проекція$D$ на$xy$ -площину.

Малюнок$\PageIndex{6}$: Тверда речовина$E$ має проекцію$D$ на$xy$ -площину типу I.

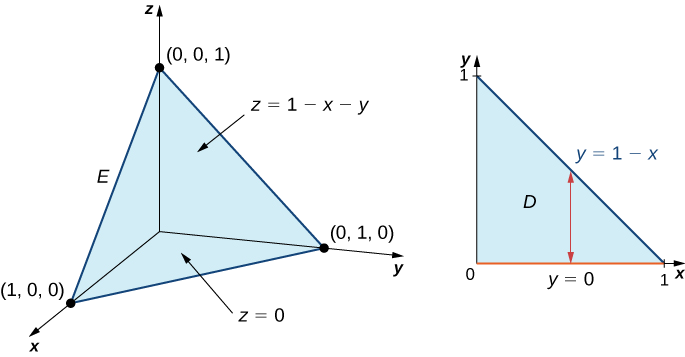
Тверду область тетраедра ми можемо описати як

$$E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber$$

Отже, потрійний інтеграл

$$\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber$$

Щоб спростити розрахунок, спочатку оцініть інтеграл$\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz$. У нас є

$$\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber$$

Тепер оцінюємо інтеграл

$$\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber$$

отримання

$$\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber$$

Нарешті оцініть

$$\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber$$

Збираючи все разом, ми маємо

$$\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber$$

Так само, як ми використовували подвійний інтеграл, $$\iint_D 1 \,dA \nonumber$$ щоб знайти площу загальної обмеженої області,$D$ ми можемо $$\iiint_E 1\,dV \nonumber$$ використовувати для пошуку об'єму загальної твердої обмеженої області$E$. Наступний приклад ілюструє метод.

Приклад$\PageIndex{3B}$: Finding a Volume by Evaluating a Triple Integral

Знайдіть об'єм правої піраміди, яка має квадратну основу в$xy$ -площині$[-1,1] \times [-1,1]$ та вершину в точці$(0, 0, 1)$, як показано на наступному малюнку.

Малюнок$\PageIndex{7}$: Знаходження обсягу піраміди з квадратною основою.

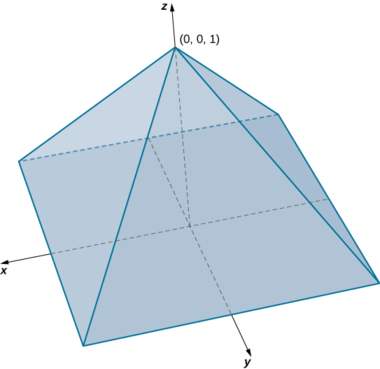
Рішення

У цій піраміді значення$z$ змінюється від 0 до 1, а на кожній$z$ висоті перетин піраміди для будь-якого значення$z$ дорівнює квадрату.

$$[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber$$

Значить, обсяг піраміди - це $$\iiint_E 1\,dV\nonumber$$ де

$$E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber$$

Таким чином, ми маємо

\ [\ почати {вирівнювати*}\ IIInt_E 1\, дВ &=\ int_ {z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z}\ int_ {x=-1+z} ^ {x = 1-z} 1\, дх\, ди\, дз\\ [5пт]
&=\ int_ {z =0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z} (2 - 2z)\, ди\, дз\\ [5пт]
&=\ int_ {z=0} ^ {z=1} (2 - 2z) ^2\, dz =\ dfrac {4} {3}. \ end {вирівнювати*}\]

Значить, обсяг піраміди -$\dfrac{4}{3}$ кубічні одиниці.

Вправа$\PageIndex{3}$

Розглянемо тверду сферу$E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}$. Запишіть потрійний інтеграл $$\iiint_E f(x,y,z) \,dV\nonumber$$ для довільної функції$f$ як ітераційний інтеграл. Потім оцініть цей потрійний інтеграл с$f(x,y,z) = 1$. Зверніть увагу, що це дає об'єм сфери за допомогою потрійного інтеграла.

Підказка

Виконайте дії в попередньому прикладі. Використовуйте симетрію.

Відповідь

$$\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}$$

Зміна порядку інтеграції

Як ми вже бачили в подвійних інтегралах над загальними обмеженими областями, зміна порядку інтеграції робиться досить часто для спрощення обчислень. При потрійному інтегралі над прямокутною коробкою порядок інтеграції не змінює рівень складності розрахунку. Однак при потрійному інтегралі над загальною обмеженою областю вибір відповідного порядку інтеграції може трохи спростити обчислення. Іноді зміна полярних координат також може бути дуже корисним. Тут ми демонструємо два приклади.

Приклад$\PageIndex{4}$: Changing the Order of Integration

Розглянемо ітераційний інтеграл

$$\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber$$

Порядок інтеграції тут спочатку по відношенню до z, потім y, а потім x. Висловлюйте цей інтеграл, змінивши порядок інтеграції, щоб бути спочатку по відношенню до$x$, потім$z$, а потім$y$. Переконайтеся, що значення інтеграла однакове, якщо ми дозволимо$f (x,y,z) =xyz$.

Рішення

Найкращий спосіб зробити це - намалювати область$E$ та її проекції на кожну з трьох координатних площин. Таким чином, нехай

$$E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber$$

і

$$\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber$$

Нам потрібно висловити цей потрійний інтеграл як

$$\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber$$

Знаючи регіон,$E$ ми можемо намалювати наступні проекції (рис.$\PageIndex{8}$):

на$xy$ -площині є$D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},$

на$yz$ -площині є$D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}$, і

на$xz$ -площині є$D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}$.

Малюнок$\PageIndex{8}$. Три поперечних перерізу$E$ на трьох координатних площині.

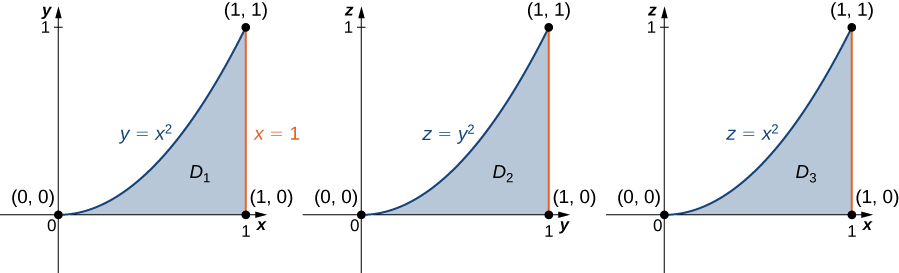
Тепер ми можемо описати ту ж область$\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}$,$E$ як і, отже, потрійний інтеграл стає

$$\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber$$

Тепер припустимо, що$f (x,y,z) = xyz$ в кожному з інтегралів. Тоді у нас є

\ [\ почати {вирівнювати*}\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ int_ {z=0} ^ {z=y^2} xyz\, dz\, dy\, dx &=\ int_ {x = 0} ^ {x=1}\ int_ {y=0} x^2}\ ліворуч. \ ліворуч [xy\ dfrac {z^2} {2}\ право|_ {z=0} ^ {z=y^2}\ праворуч]\, dy\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ ліворуч (x\ dfrac {y^5} {y=0} 2}\ праворуч) ди\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x = 1}\ ліворуч. \ ліворуч [х\ dfrac {y^6} {12}\ праворуч |_ {y=0} ^ {y=x^2}\ праворуч] dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ dfrac {x^ {13}}} {12} dx =\ ліворуч. \ dfrac {x^ {14}} {168}\ право|_ {x=0} ^ {x=1}\ [5pt]
&=\ dfrac {1} {168},\ end {align*}\]

\ [\ почати {вирівнювати*}\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ int_ {x=\ sqrt {y}} ^ {x=1} xyz\, dx\, dz\, dy &=\ int_ {y=0} ^ {y=1}\ int_ {z = 0} {z=y^2}\ ліворуч. \ ліворуч [yz\ dfrac {x^2} {2}\ право|_ {\ sqrt {y}}} ^ {1}\ праворуч] dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {z = 0} ^ {z=y^2}\ ліворуч (\ dfrac {y=0} {2} -\ dfrac {y^2z} {2}\ праворуч) дз\, ди\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ ліворуч. \ ліворуч [\ dfrac {yz^2} {4} -\ dfrac {y^2z^2} {4}\ праворуч |_ {z=0} ^ {z=y^2}\ праворуч] ди\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ ліворуч (\ dfrac {y^5} {4} -\ dfrac {y^5} {4} -\ dfrac c {y^6} {4}\ праворуч) dy\\ [5pt]
&=\ ліворуч. \ ліворуч (\ dfrac {y^6} {24} -\ dfrac {y^7} {28}\ праворуч)\ праворуч |_ {y=0} ^ {y=1}\\ [5pt]
&=\ dfrac {1} {168}. \ end {вирівнювати*}\ nonumber\]

Відповіді збігаються.

Вправа$\PageIndex{4}$

Запишіть п'ять різних ітераційних інтегралів, рівних заданому інтегралу

$$\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber$$

Підказка

Дотримуйтесь кроків у попередньому прикладі, використовуючи область$E$ як$\big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}$, і опишіть та намалюйте проекції на кожну з трьох площин, п'ять різних разів.

Відповідь

$$(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber$$

$$(iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber$$

Приклад$\PageIndex{5}$: Changing Integration Order and Coordinate Systems

Оцініть потрійний інтеграл

$$\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber$$

де$E$ - область, обмежена параболоїдом$y = x^2 + z^2$ (рис.$\PageIndex{9}$) і площиною$y = 4$.

Малюнок$\PageIndex{9}$. Інтеграція потрійного інтеграла над параболоїдом.

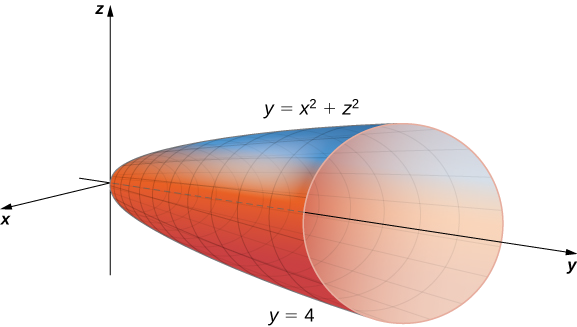
Рішення

Проекція твердої області$E$ на$xy$ -площину - це область, обмежена вище$y = 4$ і нижче параболою,$y = x^2$ як показано на малюнку.

Малюнок$\PageIndex{10}$. Перетин в$xy$ -площині параболоїда на рис$\PageIndex{9}$.

Таким чином, ми маємо

$$E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \sqrt{y - x^2} \big\}.\nonumber$$

Потрійний інтеграл стає

$$\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber$$

Цей вираз важко обчислити, тому розглянемо проекцію$E$ на$xz$ -площину. Це дисковий диск$x^2 + z^2 \leq 4$. Таким чином, отримуємо

$$\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber$$

Тут порядок інтеграції змінюється від спочатку щодо того,$z$$y$ а потім до того,$x$ щоб бути спочатку по відношенню до$y$ потім,$z$ а потім до$x$. Незабаром буде зрозуміло, наскільки ця зміна може бути корисною для обчислень. У нас є

$$\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber$$

Тепер скористайтеся полярною$x = r \, \cos \, \theta, \, z = r \, \sin \, \theta$ заміною, а$dz \, dx = r \, dr \, d\theta$ в$xz$ -площині. Це по суті те ж саме, що і коли ми використовували полярні координати в$xy$ -plane, за винятком того, що ми$y$ замінюємо на$z$. Отже, межі інтеграції змінюються, і ми маємо, використовуючи$r^2 = x^2 + z^2$,

$$\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber$$

Середнє значення функції трьох змінних

Нагадаємо, що ми знайшли середнє значення функції двох змінних шляхом оцінки подвійного інтеграла над областю на площині з подальшим діленням на площу області. Аналогічно, ми можемо знайти середнє значення функції в трьох змінних, оцінюючи потрійний інтеграл над твердою областю, а потім діливши на об'єм твердого тіла.

Середнє значення функції трьох змінних

Якщо$f(x,y,z)$ інтегрується над твердою обмеженою областю$E$ з додатним об'ємом,$V \, (E),$ то середнє значення функції дорівнює

$$f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber$$

Зверніть увагу, що гучність

$$V \, (E) = \iiint_E 1 \,dV. \nonumber$$

Приклад$\PageIndex{6}$: Finding an Average Temperature

Температура в$(x,y,z)$ точці твердого тіла,$E$ обмеженої координатними площинами і площиною$x + y + z = 1$ є$T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C}$. Знайдіть середню температуру над твердим тілом.

Рішення

Використовуйте теорему, наведену вище, і потрійний інтеграл, щоб знайти чисельник і знаменник. Потім виконайте поділ. Зверніть увагу, що літак$x + y + z = 1$ перехопив$(1,0,0), \, (0,1,0),$ і$(0,0,1)$. Регіон$E$ виглядає так

$$E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber$$

Звідси потрійний інтеграл температури

$$\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber$$

Обсяг оцінки

$$V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber$$

Звідси середнє значення

$$T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber$$ .

Вправа$\PageIndex{6}$

Знайти середнє значення функції$f(x,y,z) = xyz$ над кубом зі сторонами довжини 4 одиниці в першому октанті з однією вершиною біля початку і ребрами, паралельними осям координат.

Підказка

Виконайте дії в попередньому прикладі.

Відповідь

$f_{ave} = 8$

Ключові концепції

• Для обчислення потрійного інтеграла використовується теорема Фубіні, яка стверджує, що якщо$f(x,y,z)$ є неперервним на прямокутній коробці$B = [a,b] \times [c,d] \times [e,f]$, то $$\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber$$ і дорівнює будь-якому з п'яти інших можливих порядків для ітераційного потрійного інтеграла.
• Для обчислення об'єму загальної твердої обмеженої області$E$ використано потрійний інтеграл. $$V \, (E) = \iiint_E 1 \,dV. \nonumber$$
• Взаємозміна порядку ітераційних інтегралів не змінює відповіді. Насправді, зміна порядку інтеграції може допомогти спростити обчислення.
• Для обчислення середнього значення функції над загальною тривимірною областю ми використовуємо $$f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber$$

Ключові рівняння

• Потрійний інтеграл

$$\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber$$

Глосарій

потрійний інтеграл

потрійний інтеграл неперервної функції$f(x,y,z)$ над прямокутною суцільною коробкою$B$ - межа суми Рімана для функції трьох змінних, якщо ця межа існує