15.3: Подвійні інтеграли в полярних координатах

Цілі навчання

• Розпізнайте формат подвійного інтеграла над полярною прямокутною областю.
• Оцінити подвійний інтеграл в полярних координатах за допомогою ітераційного інтеграла.
• Розпізнайте формат подвійного інтеграла над загальною полярною областю.
• Використовуйте подвійні інтеграли в полярних координатах для обчислення площ і об'ємів.

Подвійні інтеграли іноді набагато простіше оцінити, якщо ми змінимо прямокутні координати на полярні координати. Однак перш ніж описувати, як здійснити цю зміну, нам потрібно встановити поняття подвійного інтеграла в полярній прямокутній області.

Полярні прямокутні області інтеграції

Коли ми визначили подвійний інтеграл для неперервної функції в прямокутних координатах - скажімо,$g$ над областю$R$ в$xy$ -площині - ми$R$ розділили на підпрямокутники зі сторонами, паралельними осям координат. Ці сторони мають або постійні$x$ -значення, і/або постійні$y$ -значення. У полярних координатах форма, з якою ми працюємо, - це полярний прямокутник, сторони якого мають постійні$r$ -значення та/або постійні$\theta$ -значення. Це означає, що ми можемо описати полярний прямокутник, як на малюнку$\PageIndex{1a}$, з$R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}$.

Рисунок$\PageIndex{1}$: (a) Полярний прямокутник$R$ (b), розділений на підпрямокутники$R_{ij}$ (c) Крупним планом підпрямокутника.

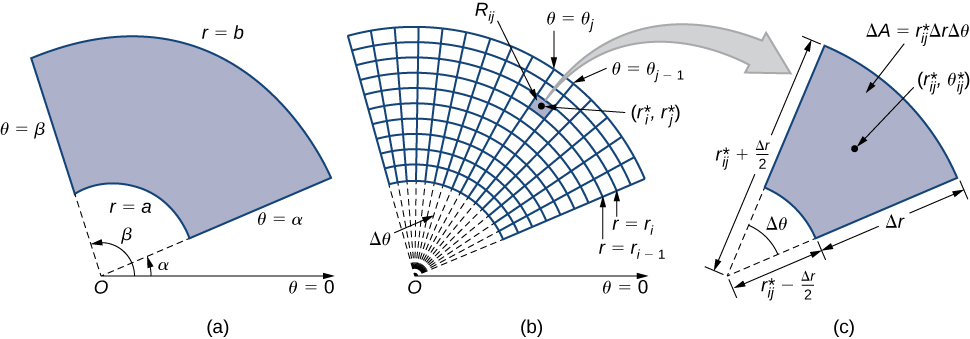
У цьому розділі ми хочемо інтегрувати над полярними прямокутниками. Розглянемо функцію$f(r,\theta)$ над полярним прямокутником$R$. Ділимо інтервал$[a,b]$ на$m$ підінтервали$[r_{i-1}, r_i]$ довжини$\Delta r = (b - a)/m$ і ділимо інтервал$[\alpha, \beta]$ на$n$ підінтервали$[\theta_{i-1}, \theta_i]$ ширини$\Delta \theta = (\beta - \alpha)/n$. Це означає, що кола$r = r_i$ і промені$\theta = \theta_i$ для$1 \leq i \leq m$ і$1 \leq j \leq n$ ділять полярний прямокутник$R$ на менші полярні підпрямокутники$R_{ij}$ (рис.$\PageIndex{1b}$).

Як і раніше, нам потрібно знайти площу$\Delta A$ полярного підпрямокутника$R_{ij}$ і «полярний» обсяг тонкої коробки вище$R_{ij}$. Нагадаємо, що в колі радіуса$r$ довжина$s$ дуги, піднесеної центральним кутом$\theta$ радіанів, дорівнює$s = r\theta$. Зверніть увагу, що полярний прямокутник$R_{ij}$ дуже схожий на трапецію з паралельними сторонами$r_{i-1}\Delta \theta$$r_i\Delta \theta$ і з шириною$\Delta r$. Звідси площа полярного$R_{ij}$ підпрямокутника

$$\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_i \Delta \theta ). \nonumber$$

Спрощення та здача

$$r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i) \nonumber$$

у нас є$\Delta A = r_{ij}^* \Delta r \Delta \theta$.

Тому полярний об'єм тонкої коробки вище$R_{ij}$ (рис.$\PageIndex{2}$)

$$f(r_{ij}^*, \theta_{ij}^*) \Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Малюнок$\PageIndex{2}$: Пошук обсягу тонкої коробки над полярним прямокутником$R_{ij}$.

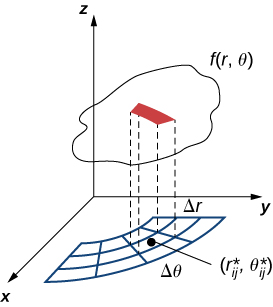
Використовуючи ту ж ідею для всіх підпрямокутників і підсумовуючи обсяги прямокутних коробок, отримаємо подвійну суму Рімана як

$$\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Як ми бачили раніше, ми отримуємо краще наближення до полярного об'єму твердого тіла над областю,$R$ коли ми пускаємо$m$ і$n$ стаємо більшими. Отже, ми визначаємо полярний об'єм як межу подвійної суми Рімана,

$$V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber$$

Це стає виразом для подвійного інтеграла.

Визначення: Подвійний інтеграл у полярних координатах

Подвійний інтеграл функції$f(r, \theta)$ над полярною прямокутною областю$R$ в$r\theta$ -площині визначається як

$$\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[4pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align} \nonumber$$

Знову ж таки, як і в розділі про подвійні інтеграли над прямокутними областями, подвійний інтеграл над полярною прямокутною областю може бути виражений як ітераційний інтеграл в полярних координатах. Отже,

$$\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta. \nonumber$$

Зверніть увагу, що вираз for$dA$ замінюється на$r \, dr \, d\theta$ при роботі в полярних координатах. Інший спосіб подивитися на полярний подвійний інтеграл полягає в зміні подвійного інтеграла в прямокутних координатах шляхом підстановки. Коли функція$f$ задається з точки зору$x$ та$y$ використання$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, і$dA = r \, dr \, d\theta$ змінює її на

$$\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta. \nonumber$$

Зауважте, що всі властивості, перераховані в розділі про подвійні інтеграли над прямокутними областями для подвійного інтеграла в прямокутних координатах, мають вірність і для подвійного інтеграла в полярних координатах, тому ми можемо використовувати їх без вагань.

Приклад$\PageIndex{1A}$: Sketching a Polar Rectangular Region

Намалюйте полярну прямокутну область

$$R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber$$

Рішення

Як ми бачимо з малюнка$\PageIndex{3}$,$r = 1$ і$r = 3$ є колами радіусом 1 і 3 і$0 \leq \theta \leq \pi$ охоплює всю верхню половину площини. Звідси область$R$ виглядає як напівкругла смуга.

Малюнок$\PageIndex{3}$: Полярна область$R$ лежить між двома півколами.

Тепер, коли ми намалювали полярну прямокутну область, давайте продемонструємо, як оцінити подвійний інтеграл над цією областю за допомогою полярних координат.

Приклад$\PageIndex{1B}$: Evaluating a Double Integral over a Polar Rectangular Region

Оцініть$\displaystyle \iint_R 3x \, dA$ інтеграл по регіону$R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.$

Рішення

Спочатку накидаємо фігуру, аналогічну малюнку$\PageIndex{3}$, але з зовнішнім радіусом$r=2$. З малюнка видно, що у нас є

$$\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta \quad\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta=0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta \quad\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta \\ &= 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}$$

Вправа$\PageIndex{1}$

Намалюйте регіон$D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}$ та оцінюйте$\displaystyle \iint_R x \, dA$.

Підказка

Дотримуйтесь інструкцій, описаних у прикладі$\PageIndex{1A}$.

Відповідь

$\frac{14}{3}$

Приклад$\PageIndex{2A}$: Evaluating a Double Integral by Converting from Rectangular Coordinates

Оцініть інтеграл

$$\iint_R (1 - x^2 - y^2) \,dA \nonumber$$

де$R$ - одинична окружність на$xy$ -площині.

Рішення

Регіон$R$ є одиничним колом, тому ми можемо описати його як$R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}$.

Використовуючи перетворення$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, і$dA = r \, dr \, d\theta$, у нас є

$$\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta \\[4pt] &= \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta \\&= \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}$$

Приклад$\PageIndex{2B}$: Evaluating a Double Integral by Converting from Rectangular Coordinates

Оцініть інтеграл $$\displaystyle \iint_R (x + y) \,dA \nonumber$$ де$R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.$

Рішення

Ми бачимо, що$R$ це кільцева область, яку можна перетворити в полярні координати і описати як$R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}$ (див. Наступний графік).

Малюнок$\PageIndex{4}$: Кільцева область інтеграції$R$.

Отже, використовуючи перетворення$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, і$dA = r \, dr \, d\theta$, у нас є

$$\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\ &= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}$$

Вправа$\PageIndex{2}$

Оцініть інтеграл$R$, $$\displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber$$ де знаходиться коло радіуса 2 на$xy$ -площині.

Підказка

Виконайте дії в попередньому прикладі.

Відповідь

$8\pi$

Загальні полярні регіони інтеграції

Для оцінки подвійного інтеграла неперервної функції за допомогою ітераційних інтегралів над загальними полярними областями розглянуто два типи областей, аналогічні типу I та типу II, що обговорюються для прямокутних координат у розділі про подвійні інтеграли над загальними регіонами. Більш часто записувати полярні рівняння як$r = f(\theta)$$\theta = f(r)$, тому ми описуємо загальну полярну область як$R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}$ (рис.$\PageIndex{5}$).

Малюнок$\PageIndex{5}$: Загальна полярна область між$\alpha \leq \theta \leq \beta$ і$h_1(\theta) \leq r \leq h_2(\theta)$.

Теорема: Подвійні інтеграли над загальними полярними областями

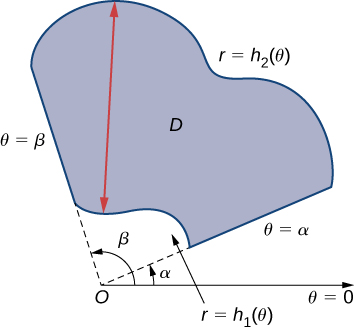
Якщо$f(r, \theta)$ суцільний на загальній полярній області,$D$ як описано вище, то

$$\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta. \nonumber$$

Приклад$\PageIndex{3}$: Evaluating a Double Integral over a General Polar Region

Оцініть інтеграл

$$\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber$$

де$D$ - область, обмежена полярної віссю і верхньою половиною кардіоїда$r = 1 + \cos \, \theta$.

Рішення

Ми можемо описати регіон$D$ так,$\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\}$ як показано на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$: Область$D$ - верхня половина кардіоїда.

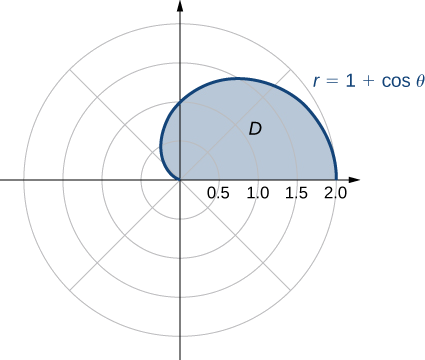
Отже, ми маємо

$$\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\ &= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ &= \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ &= - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}$$

Вправа$\PageIndex{3}$

Оцініть інтеграл

$$\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber$$

де$D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}$.

Підказка

Графік регіону і виконайте дії в попередньому прикладі.

Відповідь

$\frac{\pi}{8}$

Полярні райони та обсяги

Як і в прямокутних координатах, якщо тверде$S$ тіло обмежене поверхнею$z = f(r, \theta)$, а також поверхнями$r = a, \, r = b, \, \theta = \alpha$, і$\theta = \beta$, ми можемо знайти об'єм$S$ шляхом$V$ подвійної інтеграції, як

$$V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta. \nonumber$$

Якщо основу твердого тіла можна описати як$D = \{(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}$, то подвійним інтегралом для обсягу стає

$$V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta. \nonumber$$

Проілюструємо цю ідею деякими прикладами.

Приклад$\PageIndex{4A}$: Finding a Volume Using a Double Integral

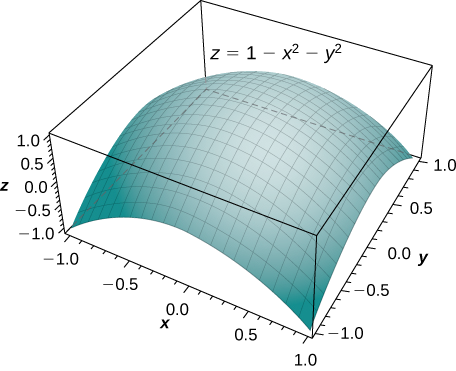
Знайдіть обсяг твердого тіла, яке лежить під параболоїдом$z = 1 - x^2 - y^2$ і над одиничною окружністю на$xy$ -площині (рис.$\PageIndex{7}$).

Малюнок$\PageIndex{7}$: Знаходження обсягу твердого тіла під параболоїдом і над одиничним колом.

Рішення

Методом подвійної інтеграції ми можемо побачити, що том є ітераційним інтегралом форми

$$\displaystyle \iint_R (1 - x^2 - y^2)\,dA \nonumber$$

де$R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}$.

Ця інтеграція була показана раніше в прикладі$\PageIndex{2A}$, тому обсяг є$\frac{\pi}{2}$ кубічними одиницями.

Приклад$\PageIndex{4B}$: Finding a Volume Using Double Integration

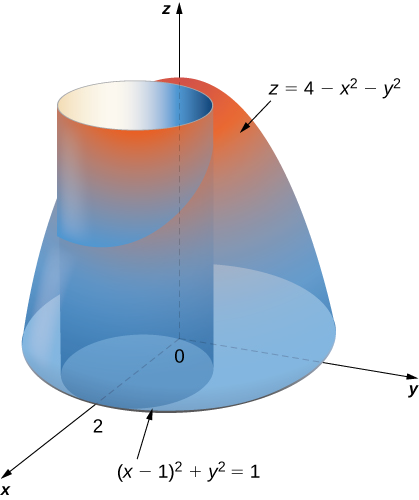
Знайдіть обсяг твердого тіла, який лежить під параболоїдом$z = 4 - x^2 - y^2$ і над диском$(x - 1)^2 + y^2 = 1$ на$xy$ -площині. Див. Параболоїд на малюнку,$\PageIndex{8}$ що перетинає циліндр$(x - 1)^2 + y^2 = 1$ над$xy$ -площиною.

Малюнок$\PageIndex{8}$: Знаходження обсягу твердого тіла з параболоїдним ковпачком і круговим підставою.

Рішення

Спочатку$(x - 1)^2 + y^2 = 1$ змініть диск на полярні координати. Розширюючи квадратний термін, ми маємо$x^2 - 2x + 1 + y^2 = 1$. Потім спростити отримати$x^2 + y^2 = 2x$, який в полярних координатах стає$r^2 = 2r \, \cos \, \theta$ і то або$r = 0$ або або$r = 2 \, \cos \, \theta$. Аналогічно змінюється рівняння параболоїда на$z = 4 - r^2$. Тому ми можемо описати диск$(x - 1)^2 + y^2 = 1$ на$xy$ -площині як область

$$D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber$$

Звідси об'єм твердого тіла, обмеженого вище параболоїдом,$z = 4 - x^2 - y^2$ а нижче$r = 2 \, \cos \theta$ -

$$\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta \\&= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\ &= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\ &= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^4\theta]\,d\theta \\&= \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}$$

Зауважте в наступному прикладі, що інтеграція не завжди проста з полярними координатами. Складність інтеграції залежить від функції, а також від регіону, над яким нам потрібно виконати інтеграцію. Якщо область має більш природний вираз в полярних координатах або якщо$f$ має більш просту антипохідну в полярних координатах, то зміна полярних координат є доречною; в іншому випадку використовуйте прямокутні координати.

Приклад$\PageIndex{5A}$: Finding a Volume Using a Double Integral

Знайдіть обсяг області, яка лежить під параболоїдом$z = x^2 + y^2$ і над трикутником, укладеним лініями$y = x, \, x = 0$, і$x + y = 2$ в$xy$ -площині.

Рішення

Спочатку досліджуємо область, над якою нам потрібно встановити подвійний інтеграл і супутній параболоїд.

Малюнок$\PageIndex{9}$: Знаходження об'єму твердого тіла під параболоїдом і над заданим трикутником.

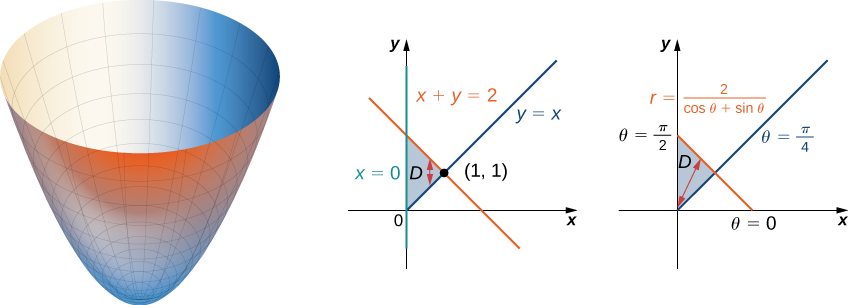
Регіон$D$ є$\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}$. Перетворення ліній$y = x, \, x = 0$, а$x + y = 2$ в$xy$ -площині в функції$r$ і у$\theta$ нас є$\theta = \pi/4, \, \theta = \pi/2$, і$r = 2 / (\cos \, \theta + \sin \, \theta)$, відповідно. Графікуючи область на$xy$ - площині, ми бачимо, що вона виглядає так$D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}$.

Тепер перетворення рівняння поверхні дає$z = x^2 + y^2 = r^2$. Тому обсяг твердого тіла задається подвійним інтегралом

$$\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta \\&= \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ (\cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta \\ &= \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta \\ &= \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right)^4 d\theta \\&= 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}$$

Як бачите, цей інтеграл дуже складний. Таким чином, ми можемо замість цього оцінити цей подвійний інтеграл в прямокутних координатах як

$$V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx. \nonumber$$

Оцінка дає

$$\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx \\&= \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 \\&= \frac{4}{3} \; \text{units}^3. \end{align*}$$

Щоб відповісти на питання про те, як знаходять формули для обсягів різних стандартних твердих тіл, таких як сфера, конус або циліндр, хочемо продемонструвати приклад і знайти обсяг довільного конуса.

Приклад$\PageIndex{5B}$: Finding a Volume Using a Double Integral

Використовуйте полярні координати, щоб знайти об'єм всередині конуса$z = 2 - \sqrt{x^2 + y^2}$ і над$xy$ -площиною.

Рішення

Область$D$ для інтеграції - це основа конуса, який, здається, є колом на$xy$ -площині (рис.$\PageIndex{10}$).

Малюнок$\PageIndex{10}$: Знаходження обсягу твердого тіла всередині конуса і над$xy$ -площиною.

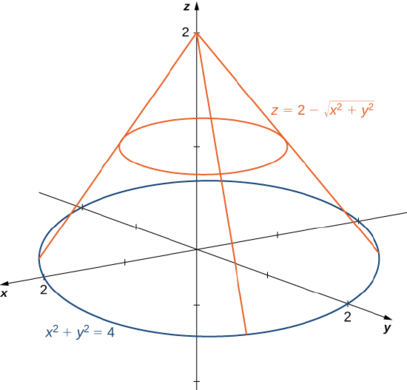
Знаходимо рівняння кола, встановивши$z = 0$:

$$\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}$$

Це означає, що радіус кола є$2$ таким для інтеграції, яку ми маємо$0 \leq \theta \leq 2\pi$ і$0 \leq r \leq 2$. Підставляємо$x = r \, \cos \theta$ і$y = r \, \sin \, \theta$ в рівняння у$z = 2 - \sqrt{x^2 + y^2}$ нас є$z = 2 - r$. Тому обсяг конуса дорівнює

$$\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber$$

Аналіз

Зверніть увагу, що якби ми знайшли об'єм довільного конуса з$\alpha$ одиницями радіуса і$h$ одиницями висоти, то рівняння конуса було б$z = h - \frac{h}{a}\sqrt{x^2 + y^2}$.

Ми все ще можемо використовувати Figure$\PageIndex{10}$ і налаштувати інтеграл як

$$\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber$$

Оцінюючи інтеграл, отримаємо$\frac{1}{3} \pi a^2 h$.

Вправа$\PageIndex{5}$

Використовуйте полярні координати, щоб знайти ітераційний інтеграл для знаходження об'єму твердого тіла, укладеного параболоїдами$z = x^2 + y^2$ і$z = 16 - x^2 - y^2$.

Підказка

Намальовування графіків може допомогти.

Відповідь

$$V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber$$

Як і у випадку з прямокутними координатами, ми також можемо використовувати полярні координати для пошуку областей певних областей за допомогою подвійного інтеграла. Як і раніше, нам потрібно зрозуміти регіон, площа якого ми хочемо обчислити. Намальовування графіка та визначення регіону може бути корисним для реалізації меж інтеграції. Як правило, формула площі в подвійній інтеграції буде виглядати так

$$\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta. \nonumber$$

Приклад$\PageIndex{6A}$: Finding an Area Using a Double Integral in Polar Coordinates

Оцініть площу, обмежену кривою$r = \cos \, 4\theta$.

Рішення

Замальовка графіка функції$r = \cos \, 4\theta$ показує, що це полярна троянда з вісьмома пелюстками (див. Наступний малюнок).

Малюнок$\PageIndex{11}$: Знаходження площі полярної троянди з вісьмома пелюстками.

Використовуючи симетрію, ми бачимо, що нам потрібно знайти площу однієї пелюстки, а потім помножити її на 8. Зверніть увагу, що значення,$\theta$ для яких графік проходить через початок, є нулями функції$\cos \, 4\theta$, а це непарні кратні$\pi/8$. Таким чином, один з пелюсток відповідає значенням$\theta$ в інтервалі$[-\pi/8, \pi/8]$. Отже, площа, обмежена кривою,$r = \cos \, 4\theta$ дорівнює

$$\begin{align*} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\ &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \\ &= 8 \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta \\&= 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] \\&= 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align*}$$

Приклад$\PageIndex{6B}$: Finding Area Between Two Polar Curves

Знайдіть область, укладену колом$r = 3 \, \cos \, \theta$ і кардіоїдом$r = 1 + \cos \, \theta$.

Рішення

В першу чергу накидайте графіки регіону (рис.$\PageIndex{12}$).

Малюнок$\PageIndex{12}$: Знаходження області, укладеної як колом, так і кардіоїдом.

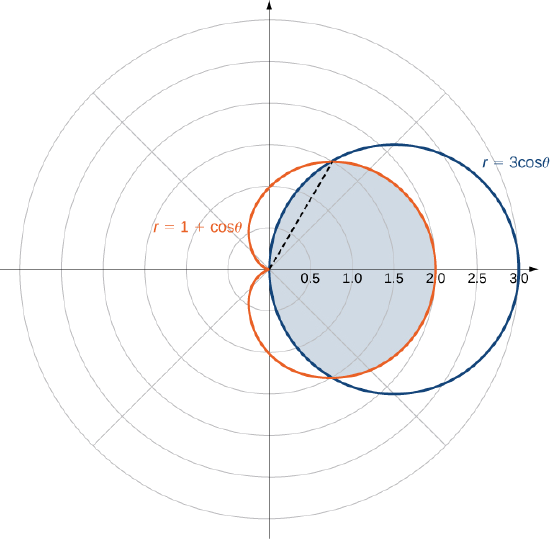
Ми можемо з бачити симетрію графіка, який нам потрібно знайти точки перетину. Встановлення двох рівнянь, рівних один одному дає

$$3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber$$

Однією з точок перетину є$\theta = \pi/3$. Площа над полярною віссю складається з двох частин, причому одна частина визначається кардіоїдом від$\theta = 0$ до,$\theta = \pi/3$ а інша частина визначається колом від$\theta = \pi/3$ до$\theta = \pi/2$. За симетрії загальна площа в два рази перевищує площу над полярною віссю. Таким чином, ми маємо

$$A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber$$

Оцінюючи кожен шматок окремо, ми виявляємо, що площа

$$A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber$$

Вправа$\PageIndex{6}$

Знайдіть область, укладену всередині кардіоїда$r = 3 - 3 \, \sin \theta$ і зовні кардіоїда$r = 1 + \sin \theta$.

Підказка

Намалюйте графік і вирішуйте для точок перетину.

Відповідь

$$A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber$$

Приклад$\PageIndex{7}$: Evaluating an Improper Double Integral in Polar Coordinates

Оцініть інтеграл

$$\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber$$

Рішення

Це неправильний інтеграл, тому що ми інтегруємо над необмеженим регіоном$R^2$. У полярних координатах вся площина$R^2$ може бути розглянута як$0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty$.

Використовуючи зміни змінних від прямокутних координат до полярних координат, ми маємо

$$\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\ &=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\ &= \frac{\pi}{10}. \end{align*}$$

Вправа$\PageIndex{7}$

Оцініть інтеграл

$$\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber$$

Підказка

Перетворити на полярну систему координат.

Відповідь

$\frac{\pi}{4}$

Ключові концепції

• Щоб застосувати подвійний інтеграл до ситуації з круговою симетрією, часто зручно використовувати подвійний інтеграл в полярних координатах. Ми можемо застосувати ці подвійні інтеграли над полярною прямокутною областю або загальною полярною областю, використовуючи ітераційний інтеграл, подібний до тих, які використовуються з прямокутними подвійними інтегралами.
• Площа$dA$ в полярних координатах стає$r \, dr \, d\theta$.
• Використовуйте$x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, і$dA = r \, dr \, d\theta$ для перетворення інтеграла в прямокутних координатах в інтеграл в полярні координати.
• Використовуйте$r^2 = x^2 + y^2$ і$\theta = tan^{-1} \left(\frac{y}{x}\right)$ для перетворення інтеграла в полярних координатах в інтеграл в прямокутні координати, якщо це необхідно.
• Щоб знайти об'єм у полярних координатах, обмежених вище поверхнею$z = f(r, \theta)$ над областю на$xy$ -площині, використовуйте подвійний інтеграл у полярних координатах.

Ключові рівняння

• Подвійний інтеграл над полярною прямокутною областю$R$

$$\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber$$

• Подвійний інтеграл над загальною полярною областю

$$\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber$$

Глосарій

полярний прямокутник

область, укладена між колами$r = a$$r = b$ і кутами$\theta = \alpha$ і$\theta = \beta$; це описується як$R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}$