12.7: Циліндричні та сферичні координати

Цілі навчання

• Перетворення від циліндричних до прямокутних координат.
• Перетворення від прямокутних до циліндричних координат.
• Перетворення від сферичних до прямокутних координат.
• Перетворення від прямокутних до сферичних координат.

Декартова система координат забезпечує простий спосіб опису розташування точок у просторі. Деякі поверхні, однак, може бути важко моделювати за допомогою рівнянь на основі декартової системи. Це знайома проблема; нагадаємо, що в двох вимірах полярні координати часто забезпечують корисну альтернативну систему опису розташування точки на площині, особливо у випадках, пов'язаних з колами. У цьому розділі ми розглянемо два різних способи опису розташування точок у просторі, обидва вони засновані на розширеннях полярних координат. Як випливає з назви, циліндричні координати корисні для вирішення проблем, пов'язаних з циліндрами, наприклад, обчислення об'єму круглого резервуара для води або кількості масла, що протікає через трубу. Аналогічно сферичні координати корисні для вирішення проблем, пов'язаних із сферами, такими як знаходження обсягу купольних конструкцій.

Циліндричні координати

Коли ми розширили традиційну декартову систему координат з двох вимірів до трьох, ми просто додали нову вісь для моделювання третього виміру. Починаючи з полярних координат, ми можемо слідувати цьому ж процесу, щоб створити нову тривимірну систему координат, яка називається циліндричною системою координат. Таким чином, циліндричні координати забезпечують природне продовження полярних координат до трьох вимірів.

Визначення: Циліндрична система координат

У циліндричній системі координат точка в просторі (рис.$\PageIndex{1}$) представлена впорядкованою трійкою$(r,θ,z)$, де

• $(r,θ)$полярні координати проекції точки в$xy$ -площині
• $z$звичайна$z$ - координата в декартовій системі координат

Малюнок$\PageIndex{1}$: Прямокутний трикутник лежить в$xy$ -площині. Довжина гіпотенузи є$r$ і$θ$ є мірою кута, утвореного позитивною$x$ -віссю і гіпотенузою. $z$-coordinate описує розташування точки над або нижче$xy$ -площини.

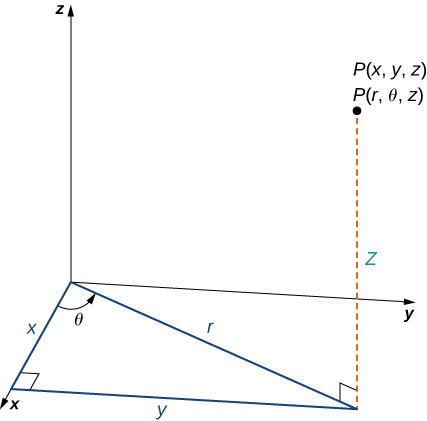
У$xy$ -площині прямокутний трикутник, показаний на малюнку,$\PageIndex{1}$ забезпечує ключ до перетворення між циліндричними та декартовими або прямокутними координатами.

Перетворення між циліндричними та декартовими координатами

Прямокутні координати$(x,y,z)$ та$(r,θ,z)$ циліндричні координати точки пов'язані наступним чином:

Ці рівняння використовуються для перетворення з циліндричних координат в прямокутні координати.

• $x=r\cos θ$
• $y=r\sin θ$
• $z=z$

Ці рівняння використовуються для перетворення з прямокутних координат в циліндричні.

1. $r^2=x^2+y^2$
2. $\tan θ=\dfrac{y}{x}$
3. $z=z$

Оскільки, коли ми обговорювали перетворення з прямокутних координат в полярні координати в двох вимірах, слід зазначити, що рівняння$\tan θ=\dfrac{y}{x}$ має нескінченну кількість розв'язків. Однак якщо$θ$ обмежитися значеннями між$0$ і$2π$, то ми можемо знайти унікальне рішення, засноване на квадранті $xy$-площини, в якій$(x,y,z)$ знаходиться вихідна точка. Зверніть увагу$x=0$, що якщо,$θ$ то значення або$\dfrac{π}{2},\dfrac{3π}{2},$ або$0$, в залежності від значення$y$.

Зверніть увагу, що ці рівняння походять від властивостей прямокутних трикутників. Щоб це було легко побачити, розглянемо точку$P$ в $xy$-площині з прямокутними координатами$(x,y,0)$ і з циліндричними координатами$(r,θ,0)$, як показано на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Теорема Піфагора забезпечує рівняння$r^2=x^2+y^2$. Відносини прямокутного трикутника говорять нам, що$x=r\cos θ, y=r\sin θ,$ і$\tan θ=y/x.$

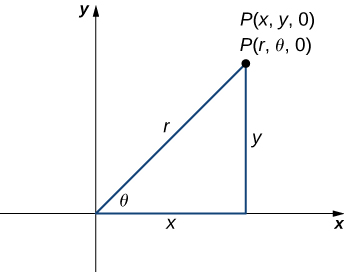
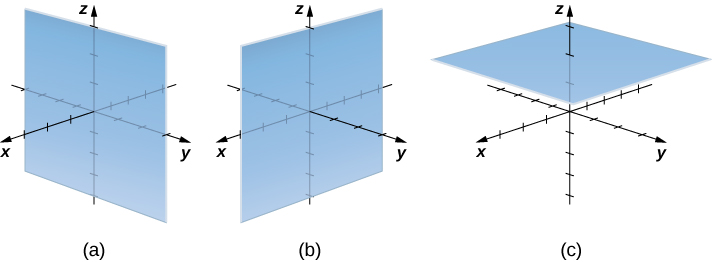
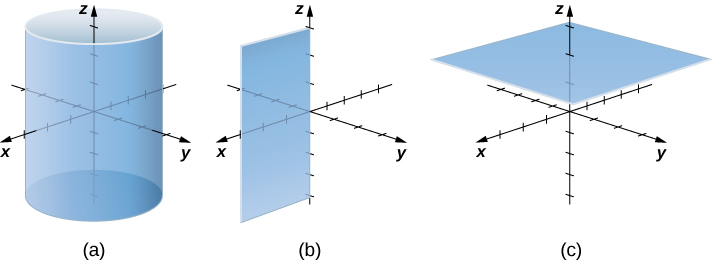
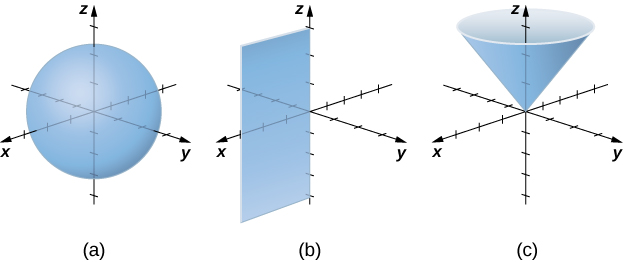
Розглянемо відмінності між прямокутними і циліндричними координатами, дивлячись на поверхні, що генеруються, коли кожна з координат тримається постійною. Якщо$c$ константа, то в прямокутних координатах поверхні форми$x=c, y=c,$ або$z=c$ є все площини. Площини цих форм паралельні$yz$ -площині,$xz$ -площині та$xy$ -площині відповідно. Коли ми перетворюємо в циліндричні координати,$z$ -coordinate не змінюється. Тому в циліндричних координатах поверхні форми$z=c$ є площинами, паралельними$xy$ -площині. Тепер давайте подумаємо про поверхні форми$r=c$. Точки на цих поверхнях знаходяться на фіксованій відстані від$z$ -осі. Іншими словами, ці поверхні представляють собою вертикальні кругові циліндри. Останній, а як щодо$θ=c$? Точки на поверхні форми$θ=c$ знаходяться під фіксованим кутом від$x$ -осі, що дає нам напівплощину, яка починається з$z$ -осі (рисунки$\PageIndex{3}$ і$\PageIndex{4}$).

Малюнок$\PageIndex{3}$: У прямокутних координатах (а) поверхні форми -$x=c$ це площини, паралельні$yz$ -площині, (б) поверхні форми$y=c$ - площини, паралельні$xz$ -площині, а (в) поверхні форми$z=c$ - площини, паралельні$xy$ -площині.

Малюнок$\PageIndex{4}$: У циліндричних координатах (а) поверхні форми$r=c$ є вертикальними циліндрами радіусу$r$, (б) поверхні форми$θ=c$ є напівплощинами під кутом$θ$ від$x$ -осі, а (в) поверхні форми$z=c$ є площинами, паралельними$xy$ - літак.

Приклад$\PageIndex{1}$: Converting from Cylindrical to Rectangular Coordinates

Покладіть точку з циліндричними координатами$(4,\dfrac{2π}{3},−2)$ і висловіть її розташування в прямокутних координатах.

Рішення

Перетворення з циліндричних координат в прямокутні вимагає простого застосування рівнянь, перелічених у Примітці:

$$\begin{align*} x &=r\cos θ=4\cos\dfrac{2π}{3}=−2 \\[4pt] y &=r\sin θ=4\sin \dfrac{2π}{3}=2\sqrt{3} \\[4pt] z &=−2 \end{align*}. \nonumber$$

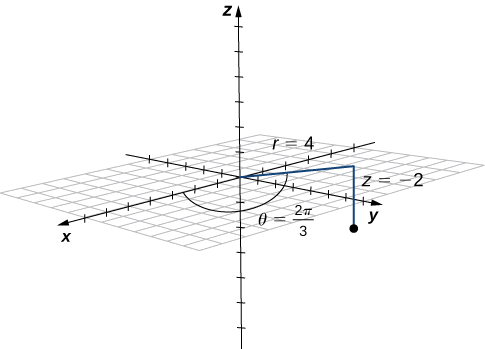
Точка з циліндричними координатами$(4,\dfrac{2π}{3},−2)$ має прямокутні координати$(−2,2\sqrt{3},−2)$ (рис.$\PageIndex{5}$).

Малюнок$\PageIndex{5}$: Проекція точки в$xy$ -площині становить 4 одиниці від початку. Лінія від початку до проекції точки утворює кут з$\dfrac{2π}{3}$ позитивною$x$ -віссю. Точка лежить$2$ одиниць нижче$xy$ -площини.

Вправа$\PageIndex{1}$

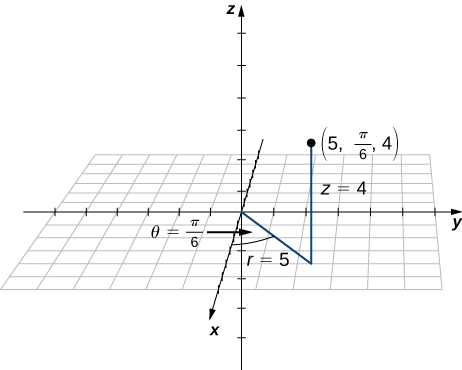
Точка$R$ має циліндричні координати$(5,\frac{π}{6},4)$. Ділянка$R$ і опишіть його розташування в просторі, використовуючи прямокутні, або декартові, координати.

Підказка

Перші дві складові відповідають полярним координатам точки в $xy$-площині.

Відповідь

Прямокутні координати точки$(\frac{5\sqrt{3}}{2},\frac{5}{2},4).$

Якщо цей процес здається знайомим, це з поважними підставами. Це точно той самий процес, який ми слідували у Вступ до параметричних рівнянь та полярних координат для перетворення з полярних координат у двовимірні прямокутні координати.

Приклад$\PageIndex{2}$: Converting from Rectangular to Cylindrical Coordinates

Перетворіть прямокутні$(1,−3,5)$ координати на циліндричні координати.

Рішення

Використовуйте другий набір рівнянь з Note для перекладу з прямокутних на циліндричні координати:

$$\begin{align*} r^2 &= x^2+y^2 \\[4pt] r &=±\sqrt{1^2+(−3)^2} \\[4pt] &= ±\sqrt{10}. \end{align*}$$

Ми вибираємо позитивний квадратний корінь,$r=\sqrt{10}$ тоб.Тепер застосовуємо формулу, щоб знайти$θ$. У цьому випадку$y$ є негативним і позитивним, а$x$ це означає, що ми повинні вибрати значення$θ$ між$\dfrac{3π}{2}$ і$2π$:

$$\begin{align*} \tan θ &=\dfrac{y}{x} &=\dfrac{−3}{1} \\[4pt] θ &=\arctan(−3) &≈5.03\,\text{rad.} \end{align*}$$

У цьому випадку z -координати однакові як у прямокутній, так і в циліндричній координатах:

$$z=5. \nonumber$$

Точка з прямокутними координатами$(1,−3,5)$ має циліндричні координати приблизно рівні$(\sqrt{10},5.03,5).$

Вправа$\PageIndex{2}$

Перетворення точки$(−8,8,−7)$ з декартових координат в циліндричні координати.

Підказка

$r^2=x^2+y^2$і$\tan θ=\frac{y}{x}$

Відповідь

$(8\sqrt{2},\frac{3π}{4},−7)$

Використання циліндричних координат поширене в таких областях, як фізика. Фізики, що вивчають електричні заряди та конденсатори, що використовуються для зберігання цих зарядів, виявили, що ці системи іноді мають циліндричну симетрію. Ці системи мають складні рівняння моделювання в декартовій системі координат, що ускладнює їх опис та аналіз. Рівняння часто можна виразити більш простими словами за допомогою циліндричних координат. Наприклад, циліндр, описаний рівнянням$x^2+y^2=25$ в декартовій системі, може бути представлений циліндричним рівнянням$r=5$.

Приклад$\PageIndex{3}$: Identifying Surfaces in the Cylindrical Coordinate System

Опишіть поверхні з заданими циліндричними рівняннями.

1. $θ=\dfrac{π}{4}$
2. $r^2+z^2=9$
3. $z=r$

Рішення

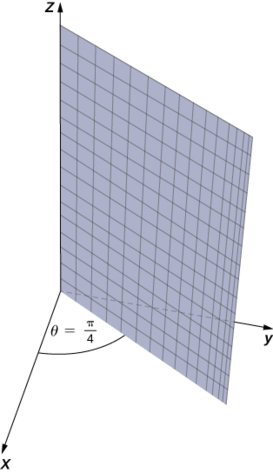
а Коли кут$θ$ утримується постійним в той час$r$ і$z$ допускається змінюватися, результатом є напівплощина (рис.$\PageIndex{6}$).

Рисунок$\PageIndex{6}$: У полярних координатах рівняння$θ=π/4$ описує промінь, що проходить по діагоналі через перший квадрант. У трьох вимірах це ж рівняння описує напівплощину.

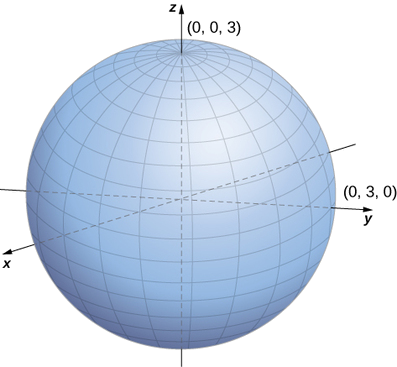
b.$r^2=x^2+y^2$ підставити в рівняння$r^2+z^2=9$, щоб висловити прямокутну форму рівняння:$x^2+y^2+z^2=9$. Це рівняння описує сферу з центром у початку з радіусом 3 (рис.$\PageIndex{7}$).

Малюнок$\PageIndex{7}$: Сфера з центром у початку координат з радіусом 3 може бути описана циліндричним рівнянням$r^2+z^2=9$.

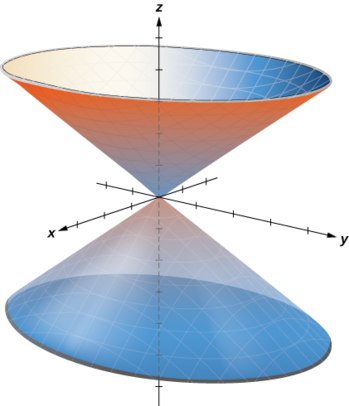
c Для опису поверхні, визначеної рівнянням$z=r$, чи корисно досліджувати сліди, паралельні$xy$ -площині. Наприклад, слід в площині$z=1$ - це коло$r=1$, слід в площині$z=3$ - коло$r=3$ і так далі. Кожен слід - це коло. Зі$z$ збільшенням значення радіус кола також збільшується. Отримана поверхня являє собою конус (рис.$\PageIndex{8}$).

Малюнок$\PageIndex{8}$: Сліди в площинях, паралельних$xy$ -площині, є колами. Радіус кіл збільшується зі$z$ збільшенням.

Вправа$\PageIndex{3}$

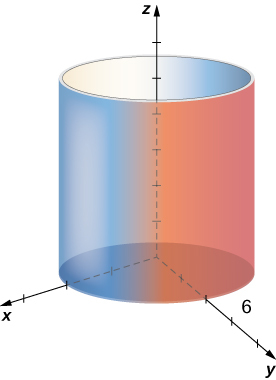
Опишіть поверхню циліндричним рівнянням$r=6$.

Підказка

$θ$І$z$ складові точок на поверхні можуть приймати будь-яке значення.

Відповідь

Ця поверхня являє собою циліндр з радіусом$6$.

Сферичні координати

У декартовій системі координат розташування точки в просторі описується за допомогою впорядкованої трійки, в якій кожна координата представляє відстань. У циліндричній системі координат розташування точки в просторі описується за допомогою двох відстаней$(r$$z)$ та вимірювання кута$(θ)$. У сферичній системі координат ми знову використовуємо впорядковану трійку для опису розташування точки в просторі. При цьому трійка описує одну відстань і два кути. Сферичні координати дозволяють легко описати сферу, так само як циліндричні координати дозволяють легко описати циліндр. Лінії сітки для сферичних координат базуються на кутових мірах, як і для полярних координат.

Визначення: сферична система координат

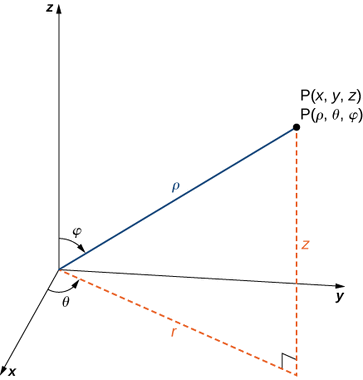
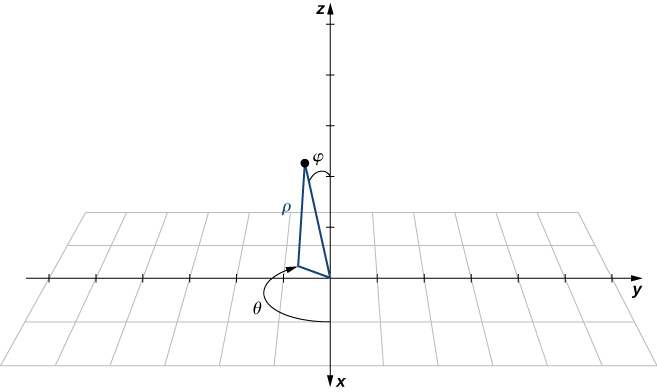
У сферичній системі координат точка$P$ в просторі (рис.$\PageIndex{9}$) представлена впорядкованою трійкою$(ρ,θ,φ)$, де

• $ρ$(Грецька буква rho) - відстань між$P$ і початком$(ρ≠0);$
• $θ$це той же кут, який використовується для опису розташування в циліндричних координатах;
• $φ$(Грецька буква phi) - кут, утворений позитивною$z$ -віссю і відрізком лінії$\bar{OP}$, де$O$ - початок і$0≤φ≤π.$

Малюнок$\PageIndex{9}$: Взаємозв'язок між сферичними, прямокутними та циліндричними координатами.

За умовністю походження представлено$(0,0,0)$ у вигляді сферичних координат.

HOWTO: Перетворення між сферичними, циліндричними та прямокутними координатами

Прямокутні координати$(x,y,z)$, циліндричні$(ρ,θ,φ)$ координати$(r,θ,z),$ та сферичні координати точки пов'язані наступним чином:

Перетворення зі сферичних координат на прямокутні координати

Ці рівняння використовуються для перетворення зі сферичних координат в прямокутні координати.

• $x=ρ\sin φ\cos θ$
• $y=ρ\sin φ\sin θ$
• $z=ρ\cos φ$

Перетворення з прямокутних координат на сферичні координати

Ці рівняння використовуються для перетворення з прямокутних координат в сферичні координати.

• $ρ^2=x^2+y^2+z^2$
• $\tan θ=\dfrac{y}{x}$
• $φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}).$

Перетворення зі сферичних координат на циліндричні координати

Ці рівняння використовуються для перетворення сферичних координат в циліндричні.

• $r=ρ\sin φ$
• $θ=θ$
• $z=ρ\cos φ$

Перетворення з циліндричних координат на сферичні координати

Ці рівняння використовуються для перетворення з циліндричних координат в сферичні координати.

• $ρ=\sqrt{r^2+z^2}$
• $θ=θ$
• $φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}})$

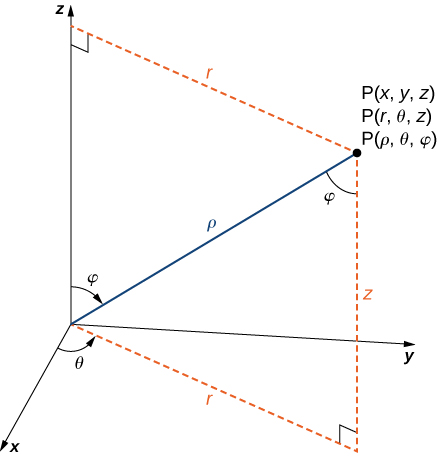
Формули для перетворення сферичних координат в прямокутні координати можуть здатися складними, але вони є простим застосуванням тригонометрії. Дивлячись на Малюнок, це легко помітити$r=ρ \sin φ$. Потім, дивлячись на трикутник в$xy$ -площині з r як його гіпотенуза, ми маємо$x=r\cos θ=ρ\sin φ \cos θ$. Виведення формули для$y$ аналогічно. Малюнок також показує, що$ρ^2=r^2+z^2=x^2+y^2+z^2$ і$z=ρ\cos φ$. Розв'язування цього останнього рівняння для,$φ$ а потім підстановка$ρ=\sqrt{r^2+z^2}$ (з першого рівняння) дає$φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}})$. Також зауважте, що, як і раніше, ми повинні бути обережними при використанні формули,$\tan θ=\dfrac{y}{x}$ щоб вибрати правильне значення$θ$.

Рисунок$\PageIndex{10}$: Рівняння, що перетворюються з однієї системи в іншу, походять від зв'язків прямокутника.

Як ми зробили з циліндричними координатами, розглянемо поверхні, які генеруються, коли кожна з координат тримається постійною. $c$Дозволяти бути постійною, і розглядати поверхні форми$ρ=c$. Точки на цих поверхнях знаходяться на фіксованій відстані від початку і утворюють сферу. Координата$θ$ в сферичній системі координат така ж, як і в циліндричній системі координат, тому поверхні форми$θ=c$ є напівплощинами, як і раніше. В останню чергу розглянемо поверхні форми$φ=0$. Точки на цих поверхнях знаходяться під фіксованим кутом від$z$ -осі і утворюють напівконус (рис.$\PageIndex{11}$).

Малюнок$\PageIndex{11}$: У сферичних координатах поверхні форми$ρ=c$ - це сфери радіусу$ρ$ (а), поверхні форми$θ=c$ - напівплощини під кутом$θ$ від$x$ -осі (b), а поверхні форми$ϕ=c$ - напівконуси під кутом$ϕ$ від $z$-вісь (c).

Приклад$\PageIndex{4}$: Converting from Spherical Coordinates

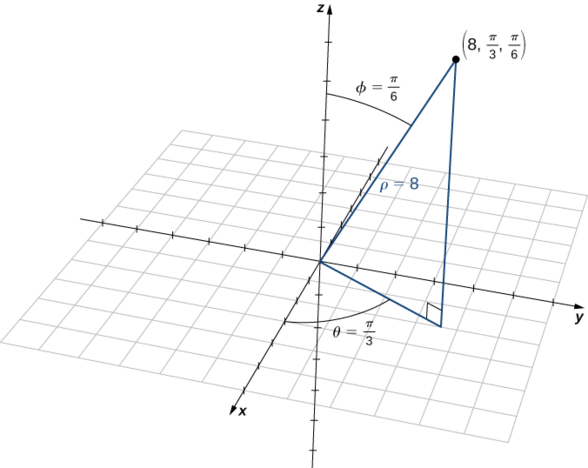
Покладіть точку зі сферичними координатами$(8,\dfrac{π}{3},\dfrac{π}{6})$ і висловіть її розташування як в прямокутних, так і в циліндричних координатах.

Рішення

Використовуйте рівняння в Примітці для перекладу між сферичними та циліндричними координатами (рис.$\PageIndex{12}$):

$$\begin{align*} x &=ρ\sin φ\cos θ \\[4pt] &=8 \sin(\dfrac{π}{6}) \cos(\dfrac{π}{3}) \\[4pt] &= 8(\dfrac{1}{2})\dfrac{1}{2} \\[4pt] &=2 \\[4pt] y &=ρ\sin φ\sin θ \\[4pt] &= 8\sin(\dfrac{π}{6})\sin(\dfrac{π}{3}) \\[4pt] &= 8(\dfrac{1}{2})\dfrac{\sqrt{3}}{2} \\[4pt] &= 2\sqrt{3} \\[4pt] z &=ρ\cos φ \\[4pt] &= 8\cos(\dfrac{π}{6}) \\[4pt] &= 8(\dfrac{\sqrt{3}}{2}) \\[4pt] &= 4\sqrt{3} \end{align*}$$

Малюнок$\PageIndex{12}$: Проекція точки в$xy$ -площині є$4$ одиницями від початку. Лінія від початку до проекції точки утворює кут з$π/3$ позитивною$x$ -віссю. Точка лежить$4\sqrt{3}$ одиниць над$xy$ -площиною.

Точка зі сферичними координатами$(8,\dfrac{π}{3},\dfrac{π}{6})$ має прямокутні координати$(2,2\sqrt{3},4\sqrt{3}).$

Знайти значення в циліндричних координатах однаково просто:

$$\begin{align*} r&=ρ \sin φ \\[4pt] &= 8\sin \dfrac{π}{6} &=4 \\[4pt] θ&=θ \\[4pt] z&=ρ\cos φ\\[4pt] &= 8\cos\dfrac{π}{6} \\[4pt] &= 4\sqrt{3} .\end{align*}$$

Таким чином, циліндричні координати для точки є$(4,\dfrac{π}{3},4\sqrt{3})$.

Вправа$\PageIndex{4}$

Побудуйте точку зі сферичними координатами$(2,−\frac{5π}{6},\frac{π}{6})$ і опишіть її розташування як в прямокутних, так і в циліндричних координатах.

Підказка

Перетворення координат в першу чергу може допомогти легше знайти розташування точки в просторі.

Відповідь

Декартова:$(−\frac{\sqrt{3}}{2},−\frac{1}{2},\sqrt{3}),$ циліндрична:$(1,−\frac{5π}{6},\sqrt{3})$

Приклад$\PageIndex{5}$: Converting from Rectangular Coordinates

Перетворіть прямокутні координати$(−1,1,\sqrt{6})$ в сферичні та циліндричні координати.

Рішення

Почніть з перетворення прямокутних координат у сферичні:

$$\begin{align*} ρ^2 &=x^2+y^2+z^2=(−1)^2+1^2+(\sqrt{6})^2=8 \\[4pt] \tan θ &=\dfrac{1}{−1} \\[4pt] ρ&=2\sqrt{2} \text{ and }θ=\arctan(−1)=\dfrac{3π}{4}. \end{align*}$$

Тому що$(x,y)=(−1,1)$, тоді правильний вибір для$θ$ є$\frac{3π}{4}$.

Насправді існує два способи ідентифікації$φ$. Ми можемо використовувати рівняння$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}})$. Більш простий підхід, однак, використовувати рівняння$z=ρ\cos φ.$ Ми знаємо, що$z=\sqrt{6}$ і$ρ=2\sqrt{2}$, так

$\sqrt{6}=2\sqrt{2}\cos φ,$так$\cos φ=\dfrac{\sqrt{6}}{2\sqrt{2}}=\dfrac{\sqrt{3}}{2}$

і тому$φ=\dfrac{π}{6}$. Сферичні координати точки$(2\sqrt{2},\dfrac{3π}{4},\dfrac{π}{6}).$

Щоб знайти циліндричні координати точки, нам потрібно всього лише знайти r:

$r=ρ\sin φ=2\sqrt{2}\sin(\dfrac{π}{6})=\sqrt{2}.$

Циліндричні координати точки є$(\sqrt{2},\dfrac{3π}{4},\sqrt{6})$.

Приклад$\PageIndex{6}$: Identifying Surfaces in the Spherical Coordinate System

Опишіть поверхні з заданими сферичними рівняннями.

1. $θ=\dfrac{π}{3}$
2. $φ=\dfrac{5π}{6}$
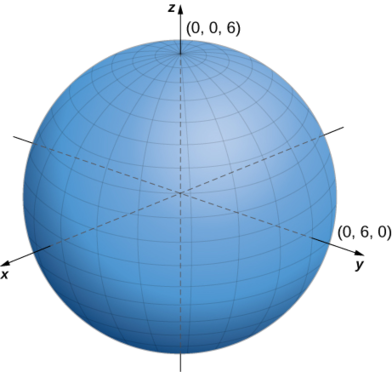
3. $ρ=6$
4. $ρ=\sin θ \sinφ$

Рішення

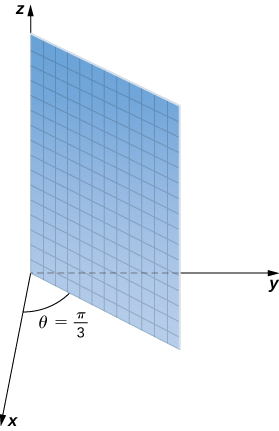
а Змінна$θ$ являє собою міру одного кута як в циліндричній, так і в сферичній системах координат. Точки з координатами$(ρ,\dfrac{π}{3},φ)$ лежать на площині, яка утворює кут$θ=\dfrac{π}{3}$ з позитивною$x$ -віссю. Тому що поверхня$ρ>0$, описана рівнянням,$θ=\dfrac{π}{3}$ є напівплощиною, показаною на малюнку$\PageIndex{13}$.

Малюнок$\PageIndex{13}$: Поверхня, описана рівнянням,$θ=\dfrac{π}{3}$ є напівплощиною.

b Рівняння$φ=\dfrac{5π}{6}$ описує всі точки сферичної системи координат, які лежать на прямій від початку, утворюючи кут вимірювання$\dfrac{5π}{6}$ rad з позитивною$z$ віссю. Ці точки утворюють напівконус (рис.). Оскільки існує лише одне значення для$φ$ того, що вимірюється від позитивної$z$ -осі, ми не отримуємо повного конуса (з двома шматочками).

Малюнок$\PageIndex{14}$: Рівняння$φ=\dfrac{5π}{6}$ описує конус.

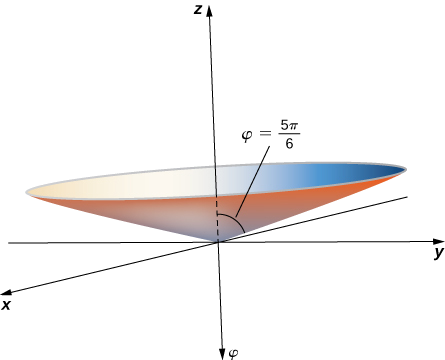
Щоб знайти рівняння в прямокутних координатах, використовуйте рівняння$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}).$

$$\begin{align*} \dfrac{5π}{6} &=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}) \\[4pt] \cos\dfrac{5π}{6}&=\dfrac{z}{\sqrt{x^2+y^2+z^2}} \\[4pt] −\dfrac{\sqrt{3}}{2}&=\dfrac{z}{\sqrt{x^2+y^2+z^2}} \\[4pt] \dfrac{3}{4} &=\dfrac{z^2}{x^2+y^2+z^2} \\[4pt] \dfrac{3x^2}{4}+\dfrac{3y^2}{4}+\dfrac{3z^2}{4} &=z^2 \\[4pt] \dfrac{3x^2}{4}+\dfrac{3y^2}{4}−\dfrac{z^2}{4} &=0. \end{align*}$$

Це рівняння конуса, зосередженого на$z$ -осі.

c Рівняння$ρ=6$ описує множину всіх точок$6$ одиниць далеко від початку—сфера з радіусом$6$ (рис.$\PageIndex{15}$).

Рисунок$\PageIndex{15}$: Рівняння$ρ=6$ описує сферу з радіусом$6$.

d Для ідентифікації цієї поверхні перетворіть рівняння зі сферичних в прямокутні координати, використовуючи рівняння$y=ρsinφ\sin θ$ і$ρ^2=x^2+y^2+z^2:$

$ρ=\sin θ \sin φ$

$ρ^2=ρ\sin θ\sin φ$Помножте обидві сторони рівняння на$ρ$.

$x^2+y^2+z^2=y$Підставляємо прямокутні змінні за допомогою рівнянь вище.

$x^2+y^2−y+z^2=0$Відніміть$y$ з обох сторін рівняння.

$x^2+y^2−y+\dfrac{1}{4}+z^2=\dfrac{1}{4}$Доповніть квадрат.

$x^2+(y−\dfrac{1}{2})^2+z^2=\dfrac{1}{4}$. Перепишіть середні терміни як ідеальний квадрат.

Рівняння описує сферу з центром у точці$(0,\dfrac{1}{2},0)$ з радіусом$\dfrac{1}{2}$.

Вправа$\PageIndex{5}$

Опишіть поверхні, визначені наступними рівняннями.

1. $ρ=13$
2. $θ=\dfrac{2π}{3}$
3. $φ=\dfrac{π}{4}$

Підказка

Подумайте про те, що представляє кожен компонент і що означає тримати цей компонент постійним.

Відповідь

Це набір всіх точок$13$ одиниць від початку. Ця множина утворює сферу з радіусом$13$.

Відповідь б

Цей набір точок утворює половину площини. Кут між половинною площиною і позитивною$x$ -віссю дорівнює$θ=\dfrac{2π}{3}.$

Відповідь c

$P$Дозволяти бути точкою на цій поверхні. Вектор положення цієї точки утворює кут з$φ=\dfrac{π}{4}$ позитивною$z$ -віссю, що означає, що точки ближче до початку знаходяться ближче до осі. Ці точки утворюють напівконус.

Сферичні координати корисні для аналізу систем, які мають певну ступінь симетрії щодо точки, наприклад об'єму простору всередині купольного стадіону або швидкості вітру в атмосфері планети. Сфера, яка має декартове рівняння,$x^2+y^2+z^2=c^2$ має просте рівняння$ρ=c$ в сферичних координатах.

У географії широта і довгота використовуються для опису місць на поверхні Землі, як показано на малюнку. Хоча форма Землі не є ідеальною сферою, ми використовуємо сферичні координати для передачі місць розташування точок на Землі. Припустимо, Земля має форму сфери з радіусом$4000$ mi. Ми виражаємо кутові заходи в градусах, а не радіанах, оскільки широта і довгота вимірюються в градусах.

Рисунок$\PageIndex{16}$: У системі широта-довгота кути описують розташування точки на Землі відносно екватора та простого меридіана.

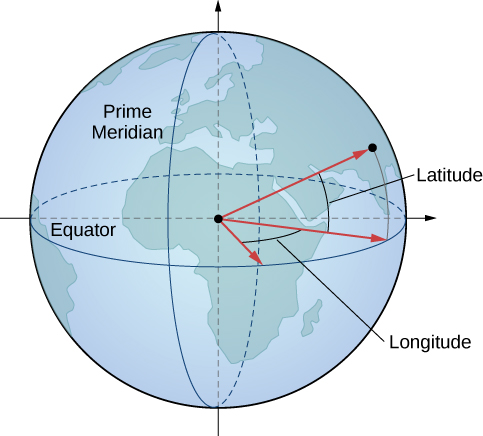
Нехай центр Землі буде центром сфери, а промінь від центру через Північний полюс представляє позитивну$z$ -вісь. Простий меридіан являє собою слід поверхні, коли вона перетинає$xz$ -площину. Екватор - це слід сфери, що перетинає$xy$ -площину.

Приклад$\PageIndex{7}$: Converting Latitude and Longitude to Spherical Coordinates

Широта Колумба, штат Огайо, -$40°$ N, а довгота$83°$ W, що означає, що Колумб знаходиться на$40°$ північ від екватора. Уявіть собі промінь з центру Землі через Колумб і промінь з центру Землі через екватор прямо на південь від Колумба. Міра кута, утвореного променями, є$40°$. Таким же чином, вимірюючи від основного меридіана, Колумб лежить$83°$ на захід. Висловіть розташування Колумба в сферичних координатах.

Рішення

Радіус Землі дорівнює$4000$ mi, так$ρ=4000$. Перетин простого меридіана і екватора лежить на позитивній$x$ -осі. Рух на захід потім описується з негативним кутом заходів, який показує, що$θ=−83°$, Оскільки Колумб лежить на$40°$ північ від екватора, він лежить на$50°$ південь від Північного полюса, так$φ=50°$. У сферичних координатах Колумб лежить в точці$(4000,−83°,50°).$

Вправа$\PageIndex{6}$

Сідней, Австралія, знаходиться в місці$34°S$ і$151°E.$ Експрес Сіднея в сферичних координатах.

Підказка

Оскільки Сідней лежить на південь від екватора, нам потрібно додати,$90°$ щоб знайти кут,$z$ виміряний від позитивної осі.

Відповідь

$(4000,151°,124°)$

Циліндричні та сферичні координати дають нам гнучкість у виборі системи координат, відповідної задачі. Вдумливий вибір системи координат може значно полегшити вирішення проблеми, тоді як поганий вибір може призвести до надмірно складних розрахунків. У наступному прикладі ми розглянемо кілька різних проблем і обговоримо, як вибрати найкращу систему координат для кожної з них.

Приклад$\PageIndex{8}$: Choosing the Best Coordinate System

У кожній з наступних ситуацій ми визначаємо, яка система координат є найбільш підходящою і опишемо, як ми б орієнтували осі координат. Там може бути більше однієї правильної відповіді на те, як повинні бути орієнтовані осі, але ми вибираємо орієнтацію, яка має сенс в контексті проблеми. Примітка: Недостатньо інформації для налаштування або вирішення цих завдань; ми просто вибираємо систему координат (рис.$\PageIndex{17}$).

1. Знайдіть центр ваги кульки для боулінгу.
2. Визначте швидкість підводного човна, що піддається океанічній течії.
3. Розрахуйте тиск в конічному резервуарі для води.
4. Знайти обсяг масла, що протікає по трубопроводу.
5. Визначте кількість шкіри, необхідної для виготовлення футболу.

Малюнок$\PageIndex{17}$: (кредит: (a) модифікація роботи scl hua, Wikimedia, (b) модифікація роботи DVIDSHUB, Flickr, (c) модифікація роботи Майкла Малака, Вікімедіа, (г) модифікація роботи Шона Мака, Вікімедіа, (е) модифікація роботи Ельверта Барнса, Flickr)

Рішення

1. Зрозуміло, що куля для боулінгу - це сфера, тому сферичні координати, ймовірно, будуть працювати тут найкраще. Походження повинно розташовуватися у фізичного центру кулі. Немає очевидного вибору того, як повинні бути орієнтовані$x$$y$ -, - і$z$ -осі. Кулі для боулінгу зазвичай мають блок ваги в центрі. Одним з можливих варіантів є вирівнювання$z$ -осі з віссю симетрії вагового блоку.
2. Підводний човен, як правило, рухається по прямій лінії. Немає обертальної або сферичної симетрії, яка застосовується в цій ситуації, тому прямокутні координати є хорошим вибором. $z$Вісь -, ймовірно, повинна вказувати вгору. Осі $x$- і$y$ -можуть бути вирівняні відповідно до точки сходу та півночі. Походження повинно бути деяким зручним фізичним розташуванням, наприклад, вихідним положенням підводного човна або місцем розташування конкретного порту.
3. Конус має кілька видів симетрії. У циліндричних координатах конус може бути представлений рівнянням$z=kr,$, де$k$ константа. У сферичних координатах ми бачили, що поверхні форми$φ=c$ є напівконусами. Останній, в прямокутних координатах, еліптичні конуси є чотирикутними поверхнями і можуть бути представлені рівняннями форми.$z^2=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}.$ У цьому випадку ми могли б вибрати будь-який з трьох. Однак рівняння для поверхні складніше в прямокутних координатах, ніж у двох інших системах, тому ми можемо уникнути цього вибору. Крім того, ми говоримо про резервуар для води, і глибина води може вступити в гру в якийсь момент наших розрахунків, тому може бути непогано мати компонент, який представляє висоту і глибину безпосередньо. Виходячи з цих міркувань, циліндричні координати можуть бути найкращим вибором. Виберіть $z$-вісь для вирівнювання з віссю конуса. Орієнтація двох інших осей довільна. Походження повинна бути нижньою точкою конуса.
4. Трубопровід - це циліндр, тому циліндричні координати будуть кращим вибором. У цьому випадку, однак, ми, швидше за все, вирішили зорієнтувати нашу $z$-вісь з центральною віссю трубопроводу. $x$-вісь може бути обрана так, щоб вказувати прямо вниз або в якомусь іншому логічному напрямку. Походження слід вибирати виходячи з постановки проблеми. Зауважте, що це ставить $z$-вісь у горизонтальну орієнтацію, що трохи відрізняється від того, що ми зазвичай робимо. Можливо, має сенс вибрати незвичайну орієнтацію для осей, якщо це має сенс для проблеми.
5. Футбол має обертальну симетрію навколо центральної осі, тому циліндричні координати працюватимуть найкраще. $z$-вісь повинна вирівнюватися з віссю кулі. Походження може бути центром кулі або, можливо, одним із кінців. Положення$x$ -осі довільне.

Вправа$\PageIndex{7}$

Яка система координат найбільш підходить для створення зоряної карти, як дивитися з Землі (див. Наступний малюнок)?

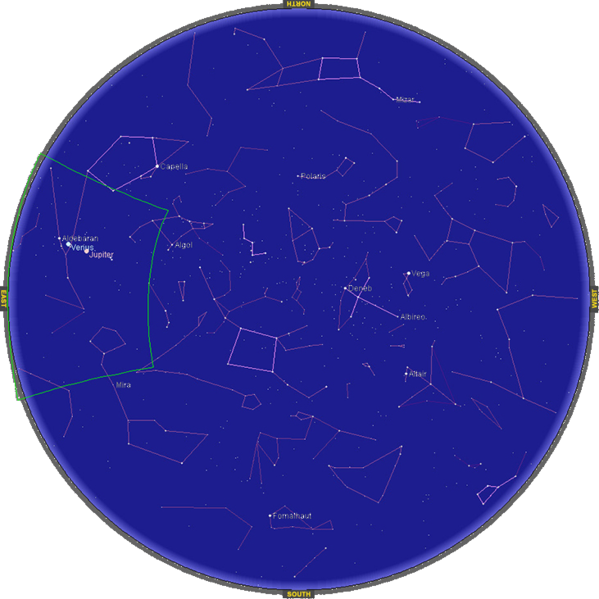
Як слід орієнтувати осі координат?

Підказка

Які види симетрії присутні в даній ситуації?

Відповідь

Сферичні координати з початком, розташованим у центрі землі,$z$ -віссю, вирівняною з Північним полюсом, і$x$ -віссю, вирівняною з простим меридіаном

Ключові поняття

• У циліндричній системі координат точка в просторі представлена впорядкованою трійкою,$(r,θ,z),$ де$(r,θ)$ представляє полярні координати проекції точки в$xy$ -площині, а z - проекцію точки на$z$ вісь -.
• Щоб перетворити точку з циліндричних координат в декартові координати, використовуйте рівняння$x=r\cos θ, y=r\sin θ,$ і$z=z.$
• Щоб перетворити точку з декартових координат в циліндричні координати, використовуйте рівняння$r^2=x^2+y^2, \tan θ=\dfrac{y}{x},$ і$z=z.$
• У сферичній системі координат точка$P$ в просторі представлена впорядкованою трійкою$(ρ,θ,φ)$, де$ρ$ відстань між$P$ і початком$(ρ≠0), θ$ - це той самий кут, який використовується для опису місця в циліндричних координатах, і$φ$ кут, утворений позитивна$z$ -вісь і відрізок лінії$\bar{OP}$, де$O$ є початком і$0≤φ≤π.$
• Щоб перетворити точку зі сферичних координат в декартові координати, використовуйте рівняння$x=ρ\sin φ\cos θ, y=ρ\sin φ\sin θ,$ і$z=ρ\cos φ.$
• Щоб перетворити точку з декартових координат в сферичні координати, використовуйте рівняння$ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},$ і$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}})$.
• Щоб перетворити точку зі сферичних координат в циліндричні координати, використовуйте рівняння$r=ρ\sin φ, θ=θ,$ і$z=ρ\cos φ.$
• Для перетворення точки з циліндричних координат в сферичні координати використовують рівняння$ρ=\sqrt{r^2+z^2}, θ=θ,$ і$φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}}).$

Глосарій

циліндрична система координат

спосіб описати місце в просторі з впорядкованою трійкою,$(r,θ,z),$ де$(r,θ)$ представляє полярні координати проекції точки в$xy$ -площині, а z представляє проекцію точки на$z$ вісь -

сферична система координат

спосіб опису розташування в просторі з впорядкованою потрійною,$(ρ,θ,φ),$ де$ρ$ відстань між$P$ і початком$(ρ≠0), θ$ - це той самий кут, який використовується для опису розташування в циліндричних координатах, і кут, утворений$φ$ позитивною$z$ віссю та лінією сегмент$\bar{OP}$, де$O$ знаходиться походження і$0≤φ≤π$

Дописувачі та атрибуція

• Template:ContribOpenStaxCalc
• Paul Seeburger edited the LaTeX on the page