12.4: Хрестовий продукт
- Page ID
- 61538
- Обчислити перехресний добуток двох заданих векторів.
- Використовуйте детермінанти для розрахунку перехресного добутку.
- Знайти вектор, ортогональний до двох заданих векторів.
- Визначте площі та обсяги за допомогою перехресного продукту.
- Обчисліть крутний момент заданого вектора сили і положення.
Уявіть собі механіка, який повертає гайковий ключ для затягування болта. Механік прикладає зусилля на кінець гайкового ключа. При цьому створюється обертання, або крутний момент, який затягує болт. Ми можемо використовувати вектори для представлення сили, прикладеної механіком, і відстані (радіуса) від болта до кінця гайкового ключа. Потім ми можемо зобразити крутний момент вектором, орієнтованим уздовж осі обертання. Зверніть увагу, що вектор крутного моменту ортогональний як вектору сили, так і вектору радіуса.
У цьому розділі ми розробляємо операцію, яка називається перехресним добутком, яка дозволяє знайти вектор, ортогональний двом заданим векторам. Розрахунок крутного моменту є важливим застосуванням поперечних виробів, і ми більш детально розглянемо крутний момент пізніше в розділі.
Перехресний продукт і його властивості
Точковий добуток - це множення двох векторів, що призводить до скаляра. У цьому розділі ми вводимо добуток двох векторів, що генерує третій вектор, ортогональний першим двом. Розглянемо, як ми можемо знайти такий вектор. \(\vecs v=⟨v_1,v_2,v_3⟩\)Дозволяти\(\vecs u=⟨u_1,u_2,u_3⟩\) і бути ненульовими векторами. Ми хочемо знайти вектор\(\vecs w=⟨w_1,w_2,w_3⟩\) ортогональний обох\(\vecs u\) і\(\vecs v\) —тобто, ми хочемо знайти\(\vecs w\) такий, що\(\vecs u ⋅ \vecs w=0\) і\( \vecs v⋅ \vecs w=0\). Тому\(w_1\),\(w_2,\) і\(w_3\) повинні задовольняти
\[u_1w_1+u_2w_2+u_3w_3=0 \label{eq1} \]
\[v_1w_1+v_2w_2+v_3w_3=0. \label{eq2} \]
Якщо помножити верхнє рівняння на\(v_3\) і нижнє рівняння на\(u_3\) і відняти, ми можемо усунути змінну\(w_3\), яка дає
\[(u_1v_3−v_1u_3)w_1+(u_2v_3−v_2u_3)w_2=0. \nonumber \]
Якщо ми виберемо
\[\begin{align*} w_1 &=u_2v_3−u_3v_2 \\[4pt] w_2 &=−(u_1v_3−u_3v_1), \end{align*}\]
отримуємо можливий вектор розв'язку. Підставляючи ці значення назад у вихідні рівняння (Рівняння\ ref {eq1} та\ ref {eq2}) дає
\[w_3=u_1v_2−u_2v_1. \nonumber \]
Тобто вектор
\[\vecs w=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩ \nonumber \]
ортогональний обох\(\vecs u\) і\(\vecs v\), що призводить нас до визначення наступної операції, яка називається перехресним добутком.
Нехай\(\vecs u=⟨u_1,u_2,u_3⟩\) і\(\vecs v=⟨v_1,v_2,v_3⟩.\) тоді, перехресний\(\vecs u×\vecs v\) добуток вектор
\[\begin{align} \vecs u×\vecs v &= (u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1) \mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \\[4pt] &=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩. \label{cross}\end{align} \]
З того, як ми розробили\(\vecs u×\vecs v\), повинно бути зрозуміло, що перехресний твір ортогональний обох\(\vecs u\) і\(\vecs v\). Однак перевірити ніколи не завадить. Щоб показати,\(\vecs u×\vecs v\) що ортогонально\(\vecs u\), обчислюємо точковий добуток\(\vecs u\) і\(\vecs u×\vecs v\).
\ [\ почати {вирівнювати*}\ векс u⋅ (\ векс u×\ векс v) &=⟨u_1, u_2, u_3⋅⟨u_2v_3−u_3v_2, −u_1v_3+u_3v_1, u_1v_2−u_2v_1⟩\ [4pt] &u_3v_1 1 (у_2в_3−у_3в_2) +у_2 (−у_1в_3+у_3в_1) +у_3 (у_1в_2−у_2в_1)\\ [4пт]
&= у_1у_2в_3−у_3в_3в_2−у_1у_2в_3+у_2в_3+_2у_3в_1+у_1у_3в_2−у_2у_3в_1\\ [4пт]
& =( u_1u_2v_3−u_1u_2 v_3) + (−u_1u_3v_2+u_1u_3v_2) + (u_2u_3v_1−u_2u_3v_1)\\ [4пт]
&= 0\ кінець {align*}\]
Аналогічним чином ми можемо показати, що хрестовий твір також ортогональний\(\vecs v\).
Нехай\(\vecs p=⟨−1,2,5⟩\) і\(\vecs q=⟨4,0,−3⟩\) (рис.\(\PageIndex{1}\)). Знайти\(\vecs p×\vecs q\).
Рішення
Підставляємо компоненти векторів в Equation\ ref {cross}:
\[\begin{align*} \vecs p×\vecs q &=⟨−1,2,5⟩×⟨4,0,−3⟩ \\[4pt] &= ⟨p_2q_3−p_3q_2,-(p_1q_3−p_3q_1),p_1q_2−p_2q_1⟩ \\[4pt] &= ⟨2(−3)−5(0),−(−1)(−3)+5(4),(−1)(0)−2(4)⟩ \\[4pt] &= ⟨−6,17,−8⟩.\end{align*}\]
Знайдіть\(\vecs p×\vecs q\) для\(\vecs p=⟨5,1,2⟩\) та\(\vecs q=⟨−2,0,1⟩.\) висловіть відповідь за допомогою стандартних одиничних векторів.
- Підказка
-
Використовуйте формулу\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)
- Відповідь
-
\(\vecs p×\vecs q = \mathbf{\hat i}−9\mathbf{\hat j}+2\mathbf{\hat k}\)
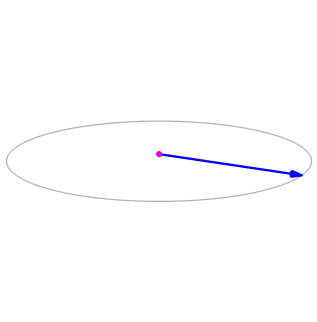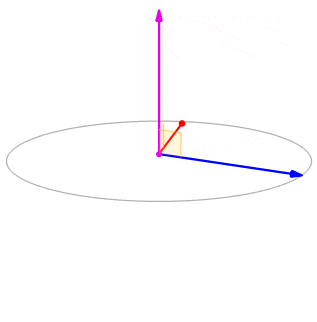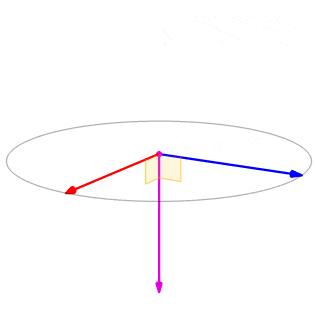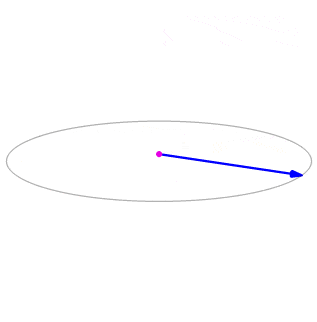
Хоча це може бути неочевидним з Equation\ ref {cross}, напрямок\(\vecs u×\vecs v\) задається правилом праворуч. Якщо провести праву руку назовні з пальцями, спрямованими в сторону\(\vecs u\), то згинаємо пальці в сторону вектора\(\vecs v\), великий палець вказує в напрямку перехресного виробу, як показано на малюнку\(\PageIndex{2}\).
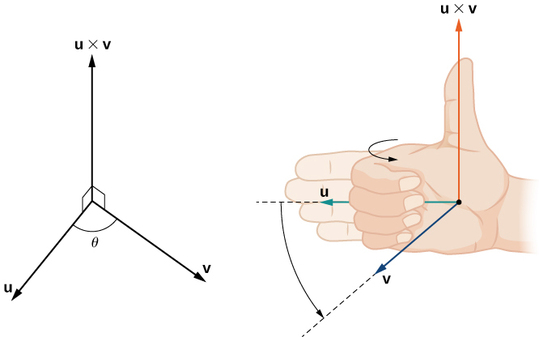
Зверніть увагу, що це означає для напрямку\(\vecs v×\vecs u\). Якщо ми застосовуємо правило правої руки до\(\vecs v×\vecs u\), ми починаємо з пальців, спрямованих у напрямку\(\vecs v\), потім скручуємо пальці в сторону вектора\(\vecs u\). При цьому великий палець вказує в протилежну сторону\(\vecs u×\vecs v\). (Спробуйте!)
Нехай\(\vecs u=⟨0,2,1⟩\) і\(\vecs v=⟨3,−1,0⟩\). Обчисліть\(\vecs u×\vecs v\)\(\vecs v×\vecs u\) і і графік їх.
Рішення
У нас є
\(\vecs u×\vecs v=⟨(0+1),−(0−3),(0−6)⟩=⟨1,3,−6⟩\)
\(\vecs v×\vecs u=⟨(−1−0),−(3−0),(6−0)⟩=⟨−1,−3,6⟩.\)
Ми бачимо, що, в даному випадку,\(\vecs u×\vecs v=−(\vecs v×\vecs u)\) (рис.\(\PageIndex{4}\)). Ми доведемо це в загальному далі в цьому розділі.
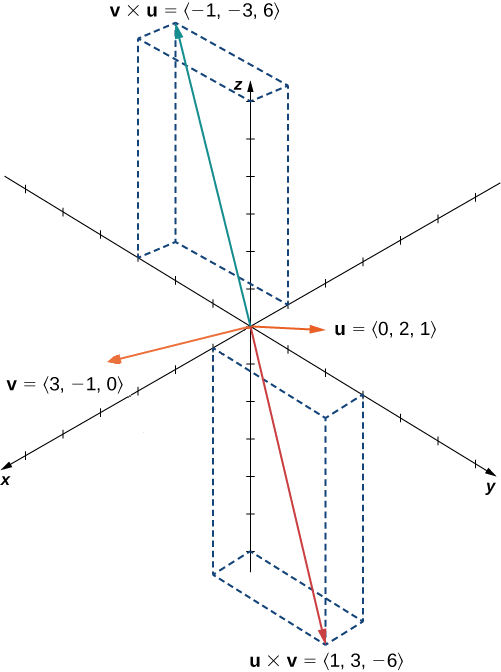
Малюнок\(\PageIndex{4}\):\(\vecs{u}×\vecs{v}\) Перехресні вироби і\(\vecs{v}×\vecs{u}\) обидва ортогональні до\(\vecs{u}\) і\(\vecs{v}\), але в протилежних напрямках.
Припустимо, вектори\(\vecs u\) і\(\vecs v\) лежать в\(xy\) -площині (\(z\)-компонент кожного вектора дорівнює нулю). Тепер припустимо, що\(x\) -\(\vecs u\) і\(y\) -компоненти і\(y\) -компонент\(\vecs v\) є позитивними, тоді як\(x\) -компонент\(\vecs v\) негативний. Припускаючи, що осі координат орієнтовані в звичайних положеннях, в якому напрямку\(\vecs u×\vecs v\) вказує?
- Підказка
-
Запам'ятайте правило правої руки (рис.\(\PageIndex{2}\)).
- Відповідь
-
Вгору (\(z\)позитивний напрямок)
Перехресні добутки стандартних\(\mathbf{\hat i}\) одиничних векторів\(\mathbf{\hat j}\), і\(\mathbf{\hat k}\) можуть бути корисні для спрощення деяких розрахунків, тому давайте розглянемо ці перехресні добутки. Просте застосування визначення показує, що
\[\mathbf{\hat i}×\mathbf{\hat i}=\mathbf{\hat j}×\mathbf{\hat j}=\mathbf{\hat k}×\mathbf{\hat k}=\vecs 0. \nonumber \]
(Перехресний добуток двох векторів є вектором, тому кожен з цих добутків призводить до нульового вектора, а не скаляра\(0\).) Перевірити розрахунки самостійно вирішувати вам.
Крім того, оскільки перехресний добуток двох векторів ортогональний кожному з цих векторів, ми знаємо, що перехресний\(\mathbf{\hat i}\)\(\mathbf{\hat j}\) добуток і паралельний\(\mathbf{\hat k}\). Аналогічно векторний\(\mathbf{\hat i}\)\(\mathbf{\hat k}\) добуток і паралельний\(\mathbf{\hat j}\), а векторний добуток\(\mathbf{\hat j}\) і\(\mathbf{\hat k}\) паралельно\(\mathbf{\hat i}\).
Ми можемо скористатися правилом правої руки, щоб визначити напрямок кожного виробу. Тоді у нас є
\ [\ почати {вирівнювати*}\ mathbf {\ капелюх я} ×\ mathbf {\ капелюх j} &=\ mathbf {\ капелюх k}\\ [4pt]
\ mathbf {\ капелюх j} ×\ mathbf {\ капелюх я} &=\ mathbf {\ капелюх k}\\ [10pt]
\ mathbf {капелюх j} ×\ mathbf {\ капелюх k} &=\ mathbf {\ капелюх я}\\ [4pt]
\ mathbf {\ капелюх k} ×\ mathbf {\ капелюх j} &=−\ mathbf {\ капелюх я}\\ [10 pt]
\ mathbf {\ капелюх k} ×\ mathbf {\ капелюх я} &=\ mathbf {\ капелюх j}\\ [4pt]
\ mathbf {\ капелюх я} ×\ mathbf {\ капелюх k} &=−\ mathbf {\ капелюх j}. \ end {вирівнювати*}\]
Ці формули стануть в нагоді пізніше.
Знайти\(\mathbf{\hat i} ×(\mathbf{\hat j}×\mathbf{\hat k})\).
Рішення
Ми це знаємо\(\mathbf{\hat j}×\mathbf{\hat k}=\mathbf{\hat i}\). Тому,\(\mathbf{\hat i}×(\mathbf{\hat j}×\mathbf{\hat k})=\mathbf{\hat i}×\mathbf{\hat i}=\vecs 0.\)
Знайти\((\mathbf{\hat i}×\mathbf{\hat j})×(\mathbf{\hat k}×\mathbf{\hat i}).\)
- Підказка
-
Запам'ятайте правило правої руки (рис.\(\PageIndex{2}\)).
- Відповідь
-
\(−\mathbf{\hat i}\)
Як ми бачили, крапковий добуток часто називають скалярним добутком, оскільки він призводить до скаляра. Перехресний добуток призводить до вектора, тому його іноді називають векторним добутком. Ці операції є обома версіями векторного множення, але вони мають дуже різні властивості і додатки. Давайте вивчимо деякі властивості крос-продукту. Доведемо лише деякі з них. Докази інших властивостей залишають як вправи.
\(\vecs u,\vecs v,\)\(\vecs w\)Дозволяти і бути вектори в просторі, і нехай\(c\) бути скалярним.
- Антикомутативне майно:\[\vecs u×\vecs v=−(\vecs v×\vecs u) \nonumber \]
- Розподільна власність:\[\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w \nonumber \]
- Множення на константу:\[c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v) \nonumber \]
- Перехресний добуток нульового вектора:\[\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0 \nonumber \]
- Перехресний добуток вектора з собою:\[\vecs v×\vecs v=\vecs 0 \nonumber \]
- Скалярний потрійний добуток:\[\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w \nonumber \]
Для власності\(i\), ми хочемо показати У\(\vecs u×\vecs v=−(\vecs v×\vecs u).\) нас є
\[\begin{align*} \vecs u×\vecs v &=⟨u_1,u_2,u_3⟩×⟨v_1,v_2,v_3⟩ \\[4pt] &=⟨u_2v_3−u_3v_2,−u_1v_3+u_3v_1,u_1v_2−u_2v_1⟩ \\[4pt] &=−⟨u_3v_2−u_2v_3,−u_3v_1+u_1v_3,u_2v_1−u_1v_2⟩ \\[4pt] &=−⟨v_1,v_2,v_3⟩×⟨u_1,u_2,u_3⟩\\[4pt] &=−(\vecs v×\vecs u).\end{align*}\]
На відміну від більшості операцій, які ми бачили, перехресний продукт не є комутативним. Це має сенс, якщо ми думаємо про правилі правої руки.
Для властивості\(iv\)., Це випливає безпосередньо з визначення перехресного добутку. У нас є
\[\vecs u × \vecs 0=⟨u_2(0)−u_3(0),−(u_1(0)−u_3(0)),u_1(0)−u_2(0)⟩=⟨0,0,0⟩=\vecs 0. \nonumber \]
Потім, за власністю i.,\(\vecs 0×\vecs u=\vecs 0\) а також. Пам'ятайте, що точковий добуток вектора і нульового вектора є скаляром\(0\), тоді як перехресний добуток вектора з нульовим вектором є вектор\(\vecs 0\).
Property\(vi\). виглядає як асоціативне властивість, але зверніть увагу на зміну операцій:
\ [\ почати {вирівнювати*}\ векс u⋅ (\ векс v×\ векс w) &=u⋅⟨v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2−v_2w_1⟩\\ [4pt]
&= u_1 (v_2w_3v_3−v_3−v_3_3_ w_2) +у_2 (−в_1w_3+v_3w_1) +у_3 (v_1w_2−v_2w_1)\\ [4pt]
&=u_1в_2w_3w_3w_1w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3_3w_3w_3_3w_3w_3_3w_3w_3_3w_3w_3_3w_3w_3_3w_3v_1w_2−u_3v_2w_1\\ [4pt]
& =( u_2v_3−u_3v _2) w_1+ (u_3v_1−u_1v_3) w_2+ (u_1v_2−u_2v_1) w_3\ [4pt]
&=⟨у_2в_3−у_3в_2, у_3в_1−у_1в_3, у_1в_2−у_2в_1 ⋅⟨w_1, w_2, w_3⟩ =(\ векс u×\ векс v) ⋅\ векс w.\ end {align*}\]
\(\square\)
Використовуйте перехресні властивості добутку для розрахунку\((2\mathbf{\hat i}×3\mathbf{\hat j})×\mathbf{\hat j}.\)
Рішення
\ [\ почати {вирівнювати*} (2\ mathbf {\ капелюх я} ×3\ mathbf {\ капелюх j}) ×\ mathbf {\ капелюх j} &= 2 (\ mathbf {\ капелюх я} ×3\ mathbf {\ капелюх j}) ×\ mathbf {\ капелюх j}\\ [4pt]
&= 2 (3) (\ mathbf {\ капелюх я} ×\ mathbf {\ капелюх j}) ×\ mathbf {\ капелюх j}\\ [4pt]
& =( 6\ mathbf {\ капелюх k}) ×\ mathbf {\ капелюх j}\\ [4pt]
&= 6 (\ mathbf { \ hat k} ×\ mathbf {\ капелюх j})\\ [4pt]
&=6 (−\ mathbf {\ капелюх я}) =−6\ mathbf {\ капелюх я}. \ end {вирівнювати*}\]
Використовуйте властивості перехресного добутку для розрахунку\((\mathbf{\hat i}×\mathbf{\hat k})×(\mathbf{\hat k}×\mathbf{\hat j}).\)
- Підказка
-
\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)
- Відповідь
-
\(−\mathbf{\hat k}\)
Поки що в цьому розділі ми займалися напрямком вектора\(\vecs u×\vecs v\), але ми не обговорювали його величину. Виявляється, існує простий вираз для величини\(\vecs u×\vecs v\) залучення величин\(\vecs u\) і\(\vecs v\), і синус кута між ними.
\(\vecs u\)\(\vecs v\)Дозволяти і бути вектори, і нехай\(θ\) кут між ними. Потім,\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ.\)
\(\vecs u=⟨u_1,u_2,u_3⟩\)\(\vecs v=⟨v_1,v_2,v_3⟩\)Дозволяти і бути вектори, і нехай\(θ\) позначають кут між ними. Тоді
\ [\ почати {вирівнювати*} ⟩\ векс u×\ векс v^2 &= (u_2v_3−u_3v_2) ^2+ (u_3v_1−u_1v_3) ^2+ (u_1v_2−u_2v_1) ^2\\ [4pt] &= u^2_2v^2_3_3_1) ^2\ [4pt]
&=u^2_2v^2_3_3
−2у_2у_3в_2в_3+у^2_3в^2_2в^2_3в^2_1у_1у_3в_3в_3+у^2_1в^2_1в^2_3+у^2_2у_1у_2в_2в_2в_2в_2+у^2_2в_2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2в^2_2_2_1\\ [4pt] &= u^2_1v^2_1+u^2_1v^2_2+u^2_1v^2_1v^2_3+u^2_2v^2_1+u^2_2v ^2_2+у^2в^2_3+у^2_3в^2_1+у^2_3в^2_2_2в^2_3в^2_2в^2_3− (u^2_1v^2_1v^2_2v^2_2v^2_3v^2_3v^2u_1u_1v_1v_1v_1v^2_v_1v_1v^2_v_2v_1v_1v_1v^2v_2v_1v_1v_1v^2v_2v_1v_2+2у_1у_3в_1в_3+2у_2у_3в_2в_3)\\ [4пт]
& =( u^2_1+u^2+u^2_2_3) (в^2_1+в^2_2+в^2_2) − (u_1v_1+u_2v_2+u_2v_3v_3v_3v_3) _3) ^2\\ [4pt]
&=⟩\ векс u^2⟩\ векс v^2− (\ векс u⋅\ векс v) ^2\\ [4pt]
&=⟩\ векс u^2⟩\ векс v^2−⟩\ векс u^2⟩\ vecs v^2\ cos^2θ\ [4pt]
&=⟩\ vecs u^2⟩\ vecs v^2 (1−\ cos^2θ)\\ [4pt]
&==\ веки u^2˚\ vecs v^2 ^ 2 (\ sin^2θ). \ end {вирівнювати*}\ nonumber\]
Беручи квадратні коріння і\(0≤θ≤180°,\) відзначаємо, що\(\sqrt{\sin^2θ}=\sinθ\) для нас є бажаний результат:
\[‖\vecs u×\vecs v‖=‖\vecs u‖‖\vecs v‖ \sin θ. \nonumber \]
□
Таке визначення перехресного продукту дозволяє візуалізувати або інтерпретувати виріб геометрично. Зрозуміло, наприклад, що перехресний добуток визначається лише для векторів у трьох вимірах, а не для векторів у двох вимірах. У двох вимірах неможливо генерувати вектор одночасно ортогональний до двох непаралельних векторів.
Використовуйте «Величина перехресного добутку», щоб знайти величину перехресного добутку\(\vecs u=⟨0,4,0⟩\) і\(\vecs v=⟨0,0,−3⟩\).
Рішення
У нас є
\ [\ почати {вирівнювати*} ⟩\ vecs u×\ vecs v⟩ &= ⟩\ vecs u⋅\ sinθ\ [4pt]
&=\ sqrt {0^2+4^2+0^2} ⋅\ sqrt {0^2+0^2+ (−3) ^2} ⋅\ sin {\ dfrac {π} 2}}\\ [4pt]
&=4 (3) (1) =12\ кінець {вирівнювати*}\]
Використовуйте «Величина перехресного продукту», щоб знайти величину\(\vecs u×\vecs v\), де\(\vecs u=⟨−8,0,0⟩\) і\(\vecs v=⟨0,2,0⟩\).
- Підказка
-
Вектори\(\vecs u\) і\(\vecs v\) є ортогональними.
- Відповідь
-
16
Детермінанти та перехресний продукт
Використання Equation\ ref {cross} для пошуку перехресного добутку двох векторів є простим, і він представляє перехресний добуток у формі корисної складової. Формула, однак, складна і важка для запам'ятовування. На щастя, у нас є альтернатива. Ми можемо обчислити перехресний добуток двох векторів, використовуючи детермінантні позначення.
А\(2×2\) детермінант визначається
\[\begin{vmatrix}a_1 & b_1\\a_2 & b_2\end{vmatrix} =a_1b_2−b_1a_2. \nonumber \]
Наприклад,
\[\begin{vmatrix}3 & −2\\5 & 1\end{vmatrix} =3(1)−5(−2)=3+10=13. \nonumber \]
\(3×3\)Детермінант визначається в терміні\(2×2\) детермінант наступним чином:
\[\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=a_1\begin{vmatrix}b_2 & b_3\\c_2 & c_3\end{vmatrix}−a_2\begin{vmatrix}b_1 & b_3\\c_1 & c_3\end{vmatrix}+a_3\begin{vmatrix}b_1 & b_2\\c_1 & c_2\end{vmatrix}.\label{expandEqn} \]
Рівняння\ ref {ExpandeQN} називається розширенням визначника вздовж першого рядка. Зверніть увагу, що множники кожного з\(2×2\) визначників у правій частині цього виразу є записами в першому рядку\(3×3\) визначника. Крім того, кожен з\(2×2\) визначників містить записи з\(3×3\) визначника, які залишаться, якщо ви перекреслили рядок і стовпець, що містять множник. Таким чином, для першого члена праворуч\(a_1\) є множник, а\(2×2\) визначник містить записи, які залишаються, якщо закреслити перший рядок і перший стовпець\(3×3\) детермінанта. Аналогічно для другого члена множник є\(a_2\), а\(2×2\) визначник містить записи, які залишаються, якщо викреслювати перший рядок і другий стовпець\(3×3\) визначника. Зверніть увагу, однак, що коефіцієнт другого члена негативний. Третій термін можна обчислити аналогічним чином.
Оцініть детермінант\(\begin{vmatrix}2 & 5 &−1\\−1 & 1 & 3\\−2 & 3 & 4\end{vmatrix}\).
Рішення
У нас є
\ [\ begin {align*}\ почати {vmatrix} 2 & 5 & −1\\ −1 & 1 & 3\\ −2 & 3\ −2 & 4\ кінець {vmatrix} &=2\ begin {vmatrix} 1\\\ кінець {vmatrix} −5\ begin {vmatrix} −1\\ begin {vmatrix} −1\\ begin vmatrix} −1 & 1\ −2 & 3\ кінець {vmatrix}\\ [4pt]
&=2 (4−9) −5 (−4+6) −1 (−3+2 )\\ [4pt]
&= 2 (−5) −5 (2) −1 (−1) =−10+1\\ [4pt]
&=−19\ end {align*}\]
Оцініть детермінант\(\begin{vmatrix}1 & −2 & −1\\3 & 2 & −3\\1 & 5 & 4\end{vmatrix}\).
- Підказка
-
Розкласти уздовж першого ряду. Не забувайте, що другий термін негативний!
- Відповідь
-
40
Технічно детермінанти визначаються тільки через масиви дійсних чисел. Однак детермінантне позначення забезпечує корисний мнемонічний пристрій для формули крос-добутку.
\(\vecs v=⟨v_1,v_2,v_3⟩\)Дозволяти\(\vecs u=⟨u_1,u_2,u_3⟩\) і бути вектори. Тоді перехресний твір\(\vecs u×\vecs v\) задається
\[\vecs u×\vecs v=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}=\begin{vmatrix}u_2 & u_3\\v_2 & v_3\end{vmatrix}\mathbf{\hat i}−\begin{vmatrix}u_1 & u_3\\v_1 & v_3\end{vmatrix}\mathbf{\hat j}+\begin{vmatrix}u_1 & u_2\\v_1 & v_2\end{vmatrix}\mathbf{\hat k}. \nonumber \]
Нехай\(\vecs p=⟨−1,2,5⟩\) і\(\vecs q=⟨4,0,−3⟩\). Знайти\(\vecs p×\vecs q\).
Рішення
Ми налаштовуємо наш детермінант, поставивши стандартні одиничні вектори по першому ряду, складові\(\vecs u\) в другому ряду та компоненти\(\vecs v\) в третьому ряду. Тоді у нас є
\ [\ почати {вирівнювати*}\ vecs p×\ vecs q &=\ почати {vmatrix}\ mathbf {\ капелюх я} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −1 & 5\ 4 & 0 & −3\ кінець {vmatrix} = почати {vmatrix} 2 & 5\\ 4 & 0\ −3\ кінець {vmatrix} 3\ кінець {vmatrix}\ mathbf {\ hat i} −\ почати {vmatrix} −1 & 5\ 4 & −3\ кінець {vmatrix}\ mathbf {\ hat j} +\ begin {vmatrix} − 1 & 2\\ 4 & 0\ кінець {vmatrix}\ mathbf {\ капелюх k}\\ [4pt]
&= (−6−0)\ mathbf {\ капелюх я} − (3−20)\ mathbf {\ капелюх j} + (0−8)\ mathbf {\ капелюх k}\\ [
4pt] &6\ mathbf f {\ шат я} +17\ mathbf {\ hat j} −8\ mathbf {\ hat k}. \ end {вирівнювати*}\]
Зверніть увагу, що ця відповідь підтверджує розрахунок перехресного добутку в прикладі\(\PageIndex{1}\).
Використовуйте детермінантні позначення, щоб знайти\(\vecs a×\vecs b\), де\(\vecs a=⟨8,2,3⟩\) і\(\vecs b=⟨−1,0,4⟩.\)
- Підказка
-
Обчисліть детермінант\(\begin{vmatrix}\mathbf{\hat i} \mathbf{\hat j} \mathbf{\hat k}\\8 & 2 & 3\\−1 & 0 & 4\end{vmatrix}\).
- Відповідь
-
\(\vecs a×\vecs b = 8\mathbf{\hat i}−35\mathbf{\hat j}+2\mathbf{\hat k}\)
Використання крос-продукту
Перехресний добуток дуже корисний для декількох типів обчислень, включаючи знаходження вектора, ортогонального двом заданим векторам, обчислення площ трикутників і паралелограмів і навіть визначення об'єму тривимірної геометричної форми, виконаної з паралелограмів, відомих як паралелепіпед. Наступні приклади ілюструють ці розрахунки.
Нехай\(\vecs a=⟨5,2,−1⟩\) і\(\vecs b=⟨0,−1,4⟩\). Знайти одиничний вектор, ортогональний обох\(\vecs a\) і\(\vecs b\).
Рішення
Перехресний\(\vecs a×\vecs b\) добуток ортогональний обом векторам\(\vecs a\) і\(\vecs b\). Ми можемо обчислити його за допомогою детермінанта:
\ [\ почати {вирівнювати*}\ vecs a×\ vecs b &=\ почати {vmatrix}\ mathbf {\ капелюх я} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ 5 & 2 & −1\\ 0 & −1 & −1\\ кінець {vmatrix} = почати {vmatrix} 2 −1\\ −1 & 4\ кінець {vmatrix}\ mathbf {\ hat i} −\ почати {vmatrix} 5 & −1\ 0 & 4\ кінець {vmatrix}\ mathbf {\ hat j} +\ begin {vmatrix} 5 & 2\\ 0 & −1\ кінець {vmatrix}\ mathbf {\ капелюх k}\\ [4pt]
& =( 8−1)\ mathbf {\ капелюх я} − (20−0)\ mathbf {\ капелюх j} + (−5−0)\ mathbf {\ капелюх k}\\ [4pt]
=7\ mathbf {\ шат я} −20\ mathbf {\ hat j} −5\ mathbf {\ hat k}. \ end {вирівнювати*}\ nonumber\]
Нормалізуйте цей вектор, щоб знайти одиничний вектор в тому ж напрямку:
\(\|\vecs a×\vecs b\|=\sqrt{(7)^2+(−20)^2+(−5)^2}=\sqrt{474}\).
Таким чином,\(\left\langle\dfrac{7}{\sqrt{474}},\dfrac{−20}{\sqrt{474}},\dfrac{−5}{\sqrt{474}}\right\rangle\) являє собою одиничний вектор, ортогональний до\(\vecs a\) і\(\vecs b\).
Спрощено, цей вектор стає\(\left\langle\dfrac{7\sqrt{474}}{474},\dfrac{−10\sqrt{474}}{237},\dfrac{−5\sqrt{474}}{474}\right\rangle\).
Знайти одиничний вектор, ортогональний обох\(\vecs a\) і\(\vecs b\), де\(\vecs a=⟨4,0,3⟩\) і\(\vecs b=⟨1,1,4⟩.\)
- Підказка
-
Нормалізувати перехресний продукт.
- Відповідь
-
\(\left\langle\dfrac{−3}{\sqrt{194}},\dfrac{−13}{\sqrt{194}},\dfrac{4}{\sqrt{194}}\right\rangle\)або, спрощено як\(\left\langle\dfrac{−3\sqrt{194}}{194},\dfrac{−13\sqrt{194}}{194},\dfrac{2\sqrt{194}}{97}\right\rangle\)
Для використання перехресного добутку для обчислення площ викладено та доведено наступну теорему.
Якщо розташувати вектори\(\vecs u\) і\(\vecs v\) такі, що вони утворюють сусідні сторони паралелограма, то площа паралелограма задається\(‖\vecs u×\vecs v‖\) (рис.\(\PageIndex{5}\)).
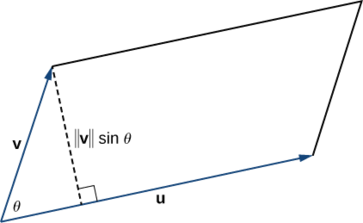
Показано, що величина перехресного добутку дорівнює базовій висоті паралелограма.
\[\begin{align*} \text{Area of a parallelogram} &= \text{base} × \text{height} \\[4pt] &=‖\vecs u‖(‖\vecs v‖\sin θ) \\[4pt] &=‖\vecs u×\vecs v‖ \end{align*}\]
□
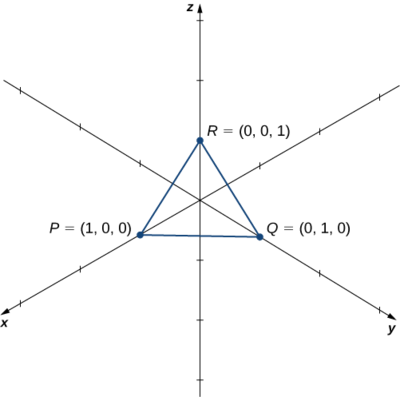
\(P=(1,0,0),Q=(0,1,0),\)\(R=(0,0,1)\)Дозволяти і бути вершинами трикутника (рис.\(\PageIndex{6}\)). Знайдіть його площу.
Рішення
У нас є\(\vecd{PQ}=⟨0−1,1−0,0−0⟩=⟨−1,1,0⟩\) і\(\vecd{PR}=⟨0−1,0−0,1−0⟩=⟨−1,0,1⟩\). Площа паралелограма з суміжними сторонами\(\vecd{PQ}\) і\(\vecd{PR}\) задається\(∥\vecd{PQ}×\vecd{PR}∥\):
\ [\ почати {вирівнювати*}\ vecd {PQ}\ раз\ vecd {PR} &=\ почати {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\\ mathbf {\ hat k}\\ −1 & 0\\ -1 & 0\\ кінець {vmatrix}\ [4pt]
&= (1−0)\ mathbf {\ капелюх я} − (−1−0)\ mathbf {\ капелюх j} + (0− (−1))\ mathbf {\ капелюх k}\\ [4pt]
&=\ mathbf {\ що я} +\ mathbf {\ капелюх j} +\ mathbf {\ капелюх k}\\ [10pt]
\ vecd {PQ} ×\ vecd {PR} &= ⟨1,1,1\\ [4pt]
&=\ квадратний {1^2+1^2+1^2}\\ [4pt]
&=\ sqrt {3}. \ end {вирівнювати*}\ nonumber\]
Площа\(ΔPQR\) дорівнює половині площі паралелограма або\(\sqrt{3}/2 \, \text{units}^2\).
Знайти площу паралелограма\( PQRS\) з вершинами\( P(1,1,0)\),\(Q(7,1,0)\),\(R(9,4,2)\), і\( S(3,4,2)\).
- Підказка
-
Намалюйте паралелограм і виділіть два вектори, які утворюють сусідні сторони паралелограма.
- Відповідь
-
\(6\sqrt{13}\, \text{units}^2\)
Потрійний скалярний добуток
Оскільки перехресний добуток двох векторів є вектором, можна об'єднати точковий добуток і перехресний добуток. Точковий добуток вектора з перехресним добутком двох інших векторів називається потрійним скалярним добутком, оскільки результат є скаляром.
Потрійний скалярний добуток векторів\( \vecs u\),\( \vecs v,\) і\(\vecs w\)
\[ \vecs u⋅( \vecs v× \vecs w). \nonumber \]
Потрійний скалярний добуток векторів
\[ \vecs u=u_1 \mathbf{\hat i}+u_2 \mathbf{\hat j}+u_3\mathbf{\hat k} \nonumber \]
\[ \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k} \nonumber \]
і
\[ \vecs w=w_1 \mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k} \nonumber \]
- визначник\(3×3\) матриці, утвореної складовими векторів:
\[ \vecs u⋅( \vecs v× \vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix}. \label{triple2} \]
Розрахунок нескладний.
\ [\ почати {вирівнювати*}\ векс u⋅ (\ векс v×\ векс w) &=⟨u_1, u_2, u_3⋅⟨v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2v_2w_1⟩\ [4pt] &u_3w_1 1 (v_2w_3−v_3w_2) +u_2 (−v_1w_3+v_3w_1) +u_3 (v_1w_2−v_2w_1)\\ [4pt]
&= u_1 (v_2w_3−v_3w_2) −u_2 (v_1w_3−v_2) _3w_1) +u_3 (v_1w_2−v_2w_1)\\ [4pt]
&=\ почати {vmatrix} u_ 1 & u_2 & u_3\\ v_1 & v_2 & v_3\\ w_1 & w_2 & w_3\ кінець {vmatrix}. \ end {вирівнювати*}\ nonumber\]
□
Нехай\(\vecs u=⟨1,3,5⟩,\,\vecs v=⟨2,−1,0⟩\) і\(\vecs w=⟨−3,0,−1⟩\). Обчисліть потрійний скалярний добуток\(\vecs u⋅(\vecs v×\vecs w).\)
Рішення
Застосовуйте рівняння\ ref {triple2} безпосередньо:
\ [\ begin {align*}\ vecs u⋅ (\ vecs v×\ vecs w) &=\ почати {vmatrix} 1 & 3\\ 2 & −1 & 0\ −3 & 0 & −1\\ кінець {vmatrix}\\ [4pt]
&=1\ begin {vmatrix} −1\ почати {vmatrix} 2 & 0\\ −3 & −1\ кінець {vmatrix} +5\ почати {vmatrix} 2 & −1\ −3 & 0\ кінець { vmatrix}\\ [4pt]
& =( 1−0) −3 (−2−0) +5 (0−3)\\ [4pt]
&=1+6−15=−8. \ end {вирівнювати*}\ nonumber\]
Обчисліть потрійний скалярний добуток\(\vecs a⋅(\vecs b×\vecs c),\) де\(\vecs a=⟨2,−4,1⟩, \vecs b=⟨0,3,−1⟩\), і\(\vecs c=⟨5,−3,3⟩.\)
- Підказка
-
Помістіть вектори як рядки\(3×3\) матриці, а потім обчислите детермінант.
- Відповідь
-
\(17\)
Коли ми створюємо матрицю з трьох векторів, ми повинні бути обережними щодо порядку, в якому ми перераховуємо вектори. Якщо перерахувати їх в матрицю в одному порядку, а потім переставити рядки, абсолютне значення визначника залишається незмінним. Однак кожен раз, коли два ряди змінюються місцями, визначник змінює знак:
\(\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\a_1 & a_2 & a_3\\c_1 & c_2 & c_3\end{vmatrix}=−d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\c_1 & c_2 & c_3\\a_1 & a_2 & a_3\end{vmatrix}=d \quad\quad \begin{vmatrix}c_1 & c_2 & c_3\\b_1 & b_2 & b_3\\a_1 & a_2 & a_3\end{vmatrix}=−d\)
Перевірити цей факт просто, але досить безладно. Давайте розглянемо це на прикладі:
\ [\ begin {align*}\ почати {vmatrix} 1 & 2\\ −2 & 0 & 3\\ 4 & 1 & −1\ кінець {vmatrix} &=\ почати {vmatrix} 0 & 3\\ 1 & −1\ кінець {vmatrix} −2\ begin {vmatrix} −2 & 3\\ 4 & −1\ кінець {vmatrix} +\ {почати {vmatrix} −2 & 3\\ 4 & −1\ кінець {vmatrix} +\ {почати} −2 & 0\\ 4 & 1\ кінець {vmatrix}\\ [4pt]
& =( 0−3) −2 (2−12) + (−2−0)\\ [4pt]
&=−3+20−2=15. \ end {вирівнювати*}\ nonumber\]
Перемикання двох верхніх рядів у нас є
\ [\ почати {вирівнювати*}\ почати {vmatrix} −2 & 0 & 3\\ 1 & 2 & 1\ 4 & 1 & −1\ кінець {vmatrix} &=-2\ почати {vmatrix} 2 & 1\ 1\ кінець {vmatrix} +3\ почати {vmatrix} 1 & 2\\ 4 & 1\ кінець {vmatrix}\ [4pt]
=−2 (−2−1) +3 (1−8)\\ [4pt]
&=6−21=−15. \ end {вирівнювати*}\ nonumber\]
Перестановка векторів у потрійних добутках еквівалентна переупорядкуванню рядків у матриці детермінанти. Дозвольте\(\vecs u=u_1\mathbf{\hat i}+u_2\mathbf{\hat j}+u_3\mathbf{\hat k}, \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k},\) і\(\vecs w=w_1\mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k}.\) застосовуючи примітку, у нас є
\[\vecs u⋅(\vecs v×\vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix} \nonumber \]
і
\[\vecs u⋅(\vecs w×\vecs v)=\begin{vmatrix}u_1 & u_2 & u_3\\w_1 & w_2 & w_3\\v_1 & v_2 & v_3\end{vmatrix}. \nonumber \]
Ми можемо отримати детермінант для обчислення\(\vecs u⋅(\vecs w×\vecs v)\) шляхом перемикання нижніх двох рядків\(\vecs u⋅(\vecs v×\vecs w).\) Тому,\(\vecs u⋅(\vecs v×\vecs w)=−\vecs u⋅(\vecs w×\vecs v).\)
Після цього міркування та вивчення різних способів обміну змінними у потрійному скалярному добутку призводять до наступних ідентичностей:
\ [\ почати {вирівняти}\ векс u⋅ (\ векс v×\ векс w) &=−\ векс u⋅ (\ векс w×\ vecs v)\\ [10pt]
\ vecs u⋅ (\ vecs v×\ vecs w) &=\ vecs v⋅ (\ vecs w ×\ vecs u) =\ vecs w⋅ (\ vecs w ×\ vecs v). \ end {вирівняти}\ nonumber\]
\(\vecs v\)Дозволяти\(\vecs u\) і бути два вектори в стандартному положенні. Якщо\(\vecs u\) і не\(\vecs v\) є скалярними кратними один одному, то ці вектори утворюють сусідні сторони паралелограма. Ми бачили в Примітка, що площа цього паралелограма є\(‖\vecs u×\vecs v‖\). Тепер припустимо, ми додамо третій вектор\(\vecs w\), який не лежить в тій же площині, що\(\vecs u\) і,\(\vecs v\) але все ще розділяє ту саму початкову точку. Потім ці вектори утворюють три ребра паралелепіпеда, тривимірну призму з шістьма гранями, які є кожним паралелограмом, як показано на малюнку\(\PageIndex{7}\). Обсяг цієї призми - добуток висоти фігури і площі її підстави. Потрійний скалярний\(\vecs w\) добуток\(\vecs u,\vecs v,\) і надає простий метод розрахунку обсягу паралелепіпеда, визначеного цими векторами.
Обсяг паралелепіпеда з сусідніми ребрами, заданий векторами\(\vecs u,\vecs v\), і\(\vecs w\) є абсолютним значенням потрійного скалярного добутку (рис.\(\PageIndex{7}\)):
\[V=||\vecs u⋅(\vecs v×\vecs w)||. \nonumber \]
Зауважимо, що, як видно з назви, потрійний скалярний твір виробляє скаляр. Щойно представлена формула об'єму використовує абсолютне значення скалярної величини.
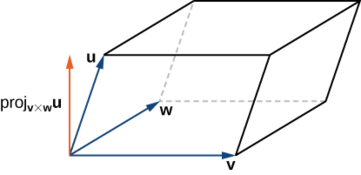
Площа підстави паралелепіпеда задається\(‖\vecs v×\vecs w‖.\) по Висота фігури задається Обсяг паралелепіпеда - добуток висоти і площі підстави, тому ми маємо\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\)
\ [\ почати {вирівнювати*} V &=\ текст {proj} _ {\ vecs v×\ vecs w}\ vecs u⟩\ vecs v×\ vecs w⟩\ [4pt]
&=\ dfrac {\ vecs u⋅ (\ vecs v ×\ vecs w)} {\ vecs v×\ векс v×\ векс w⟩\\ [4pt]
&=\ |\ vecs u⋅ (\ векс v×\ vecs w)\ |. \ end {вирівнювати*}\]
□
Нехай\(\vecs u=⟨−1,−2,1⟩,\vecs v=⟨4,3,2⟩,\) і\(\vecs w=⟨0,−5,−2⟩\). Знайдіть обсяг паралелепіпеда з сусідніми ребрами\(\vecs u,\vecs v\), і\(\vecs w\) (рис.\(\PageIndex{8}\)).
Рішення
У нас є
\ [\ почати {вирівнювати*}\ vecs u⋅ (\ vecs v×\ vecs w) &=\ почати {vmatrix} −1 & −2 & 1\\ 4 & 3\\ 0 & −5 & −2\ кінець {vmatrix}\\ [4pt]
&= (−1)\ почати {vmatrix} 3 & 2\ −5 & −2\\ кінець {vmatrix {vmatrix {vmatrix} +2\ почати {vmatrix} 4 & 2\ 0 & −2\ кінець {vmatrix} +\ begin {vmatrix} 4 & 3\\ 0 & −5\ кінець { vmatrix}\\ [4pt]
& =( −1) (−6+10) +2 (−8−0) + (−20−0)\\ [4pt]
&=−4−16−20\ [4pt]
&=−40. \ end {вирівнювати*}\]
Таким чином, обсяг паралелепіпеда дорівнює\(|−40|=40\) одиницям 3
Знайти об'єм паралелепіпеда, утвореного векторами\(\vecs a=3\mathbf{\hat i}+4\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=2\mathbf{\hat i}−\mathbf{\hat j}−\mathbf{\hat k},\) і\(\vecs c=3\mathbf{\hat j}+\mathbf{\hat k}.\)
- Підказка
-
Обчисліть потрійний скалярний добуток, знайшовши детермінант.
- Відповідь
-
\(8\)одиниць 3
Застосування крос-продукту
Поперечний твір з'являється в багатьох практичних застосуваннях в математиці, фізиці та інженерії. Давайте розглянемо деякі з цих додатків тут, включаючи ідею крутного моменту, з якої ми і почали цей розділ. Інші програми з'являються в наступних розділах, особливо в нашому дослідженні векторних полів, таких як гравітаційні та електромагнітні поля (Вступ до векторного числення).
Використовуйте потрійний скалярний добуток, щоб показати\(\vecs u=⟨2,0,5⟩,\vecs v=⟨2,2,4⟩\), що вектори і\(\vecs w=⟨1,−1,3⟩\) є компланарними, тобто показати, що ці вектори лежать в одній площині.
Рішення
Почніть з обчислення потрійного скалярного добутку, щоб знайти об'єм паралелепіпеда, визначеного\(\vecs u,\vecs v,\) і\(\vecs w\):
\ [\ почати {вирівнювати*}\ vecs u⋅ (\ vecs v×\ vecs w) &=\ почати {vmatrix} 2 & 0\ 2 & 4\\ 1 & −1 & 3\ end {vmatrix}\\ [4pt]
&= [2 (2) (3) + (0) (4) (1) +5 (2) (2) (1) +5 (2) (1) (2) (1) (2) (1) (2) - 1] − [5 (2) (1) + (2) (4) (−1) + (0) (2) (3)]\\ [4pt]
&=2−2 =0. \ end {вирівнювати*}\]
Обсяг паралелепіпеда дорівнює\(0\) одиницям 3, тому один з розмірів повинен дорівнювати нулю. Тому всі три вектори лежать в одній площині.
Чи є вектори\(\vecs a=\mathbf{\hat i}+\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=\mathbf{\hat i}−\mathbf{\hat j}+\mathbf{\hat k},\) і\(\vecs c=\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}\) компланарні?
- Підказка
-
Обчисліть потрійний скалярний добуток.
- Відповідь
-
Ні, потрійний скалярний\(−4≠0,\) добуток так три вектори утворюють сусідні краї паралелепіпеда. Вони не є копланарними.
Лише одна площина може проходити через будь-яку множину з трьох неколінеарних точок. Знайти вектор, ортогональний площині, що містить точки\(P=(9,−3,−2),Q=(1,3,0),\) і\(R=(−2,5,0).\)
Рішення
Площина повинна містити вектори\(\vecd{PQ}\) і\(\vecd{QR}\):
\(\vecd{PQ}=⟨1−9,3−(−3),0−(−2)⟩=⟨−8,6,2⟩\)
\(\vecd{QR}=⟨−2−1,5−3,0−0⟩=⟨−3,2,0⟩.\)
Перехресний\(\vecd{PQ}×\vecd{QR}\) добуток створює вектор, ортогональний обох\(\vecd{PQ}\) і\(\vecd{QR}\). Тому перехресний добуток ортогональний площині, яка містить ці два вектори:
\ [\ почати {вирівнювати*}\ vecd {PQ} ×\ vecd {QR} &=\ почати {vmatrix}\ mathbf {\ капелюх я} &\ mathbf {\ hat j} &\\ mathbf {\ капелюх k}\\ −8 & 2\\ −3 & 2\ 0\ кінець {vmatrix}\\ [
4pt] &0\ mathbf {\ капелюх я} −6\ mathbf {\ капелюх j} −16\ mathbf {\ капелюх k} − (−18\ mathbf {\ капелюх k} +4\ mathbf {\ шат я} +0\ mathbf {\ капелюх j})\\ [4pt]
&=−4\ mathbf {\ капелюх я} −6\ mathbf {\ hat j} +2\ mathbf {\ hat k}. \ end {вирівнювати*}\]
Ми бачили, як використовувати потрійний скалярний добуток і як знайти вектор, ортогональний площині. Тепер ми застосовуємо крос-продукт до реальних ситуацій.
Іноді сила змушує об'єкт обертатися. Наприклад, поворот викрутки або гайкового ключа створює такий обертальний ефект, званий крутним моментом.
Крутний момент\(\vecs \tau\) (грецька буква тау) вимірює тенденцію сили виробляти обертання навколо осі обертання. \(\vecs r\)Дозволяти вектор з початковою точкою, розташованої на осі обертання і з кінцевою точкою, розташованої в точці, де сила прикладена, і нехай вектор\(\vecs F\) представляє силу. Тоді крутний момент дорівнює перехресному добутку\(r\) і\(F\):
\[\vecs \tau=\vecs r×\vecs F. \nonumber \]
Див\(\PageIndex{9}\). Малюнок.
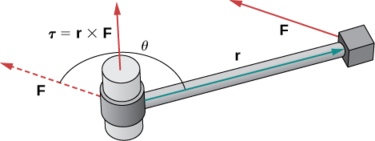
Подумайте про те, щоб закрутити болт за допомогою гайкового ключа. Крутний момент τ, що додається до болта, залежить від того, наскільки сильно ми натискаємо гайковий ключ (зусилля) і наскільки далеко до рукоятки ми докладаємо зусилля (відстань). Крутний момент збільшується з більшим зусиллям на гайковий ключ на більшій відстані від болта. Загальними одиницями крутного моменту є ньютон-метр або фут-фунт. Хоча крутний момент розмірно еквівалентний роботі (він має однакові одиниці), ці два поняття відрізняються. Крутний момент використовується спеціально в контексті обертання, тоді як робота зазвичай передбачає рух уздовж лінії.
Затягують болт, приклавши зусилля\(6\) N до гайкового ключа 0,15-м (рис.\(\PageIndex{10}\)). Кут між гайковим ключем і вектором сили дорівнює\(40°\). Знайдіть величину крутного моменту близько центру болта. Округляйте відповідь до двох знаків після коми.
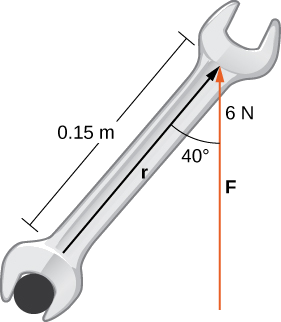
Рішення:
Підставляємо задану інформацію в рівняння, що визначає крутний момент:
\ [\ почати {вирівнювати*} ⟩\ векс τ &=\ |\ векс r ×\ векс F\ |\\ [4pt]
&= =\ векс r\ vecs F\ sinθ\\ [4pt]
& =( 0,15\,\ текст {м}) (6\,\ текст {N})\ sin 40°\ [4pt]
&≈0.58\,\ текст {n⋅м.} \ end {вирівнювати*}\]
Розрахуйте зусилля, необхідне для отримання\(15\) Н⋅м крутного моменту під кутом\(30º\) від\(150\) -см стрижня.
- Підказка
-
\(‖\vecs τ‖=15\)н⋅м і\(‖\vecs r‖=1.5\) м
- Відповідь
-
\(20\)N
Ключові концепції
- Перехресний\(\vecs u×\vecs v\) добуток двох векторів\(\vecs u=⟨u_1,u_2,u_3⟩\) і\(\vecs v=⟨v_1,v_2,v_3⟩\) являє собою вектор, ортогональний обох\(\vecs u\) і\(\vecs v\). Його довжина задається тим\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ,\), де\(θ\) кут між\(\vecs u\) і\(\vecs v\). Його напрямок задається правилом правої руки.
- Алгебраїчна формула для обчислення перехресного добутку двох векторів
\(\vecs u=⟨u_1,u_2,u_3⟩\)і\(\vecs v=⟨v_1,v_2,v_3⟩\), є
\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)
- Перехресний добуток задовольняє наступним властивостям векторів\(\vecs u,\vecs v,\) і\(\vecs w\), і скалярних\(c\):
\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)
\(\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w\)
\(c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v)\)
\(\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0\)
\(\vecs v×\vecs v=\vecs 0\)
\(\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w\)
- Перехресний добуток векторів\(\vecs u=⟨u_1,u_2,u_3⟩\) і\(\vecs v=⟨v_1,v_2,v_3⟩\) є детермінантою\(\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}\)
- Якщо вектори\(\vecs u\) і\(\vecs v\) утворюють сусідні сторони паралелограма, то площа паралелограма задається\(\|\vecs u×\vecs v\|.\)
- Потрійний скалярний добуток векторів\(\vecs u, \vecs v,\) і\(\vecs w\)\(\vecs u⋅(\vecs v×\vecs w).\)
- Обсяг паралелепіпеда з сусідніми ребрами, заданий векторами\(\vecs u,\vecs v\), і\(\vecs w\) дорівнює\(V=|\vecs u⋅(\vecs v×\vecs w)|.\)
- Якщо потрійний скалярний добуток векторів\(\vecs u,\vecs v,\) і\(\vecs w\) дорівнює нулю, то вектори є компланарними. Вірно і зворотне: якщо вектори компланарні, то їх потрійний скалярний добуток дорівнює нулю.
- Перехресний добуток може бути використаний для ідентифікації вектора, ортогонального до двох заданих векторів або до площини.
- Крутний момент\(\vecs τ\) вимірює тенденцію сили виробляти обертання навколо осі обертання. Якщо сила\(\vecs F\) діє на відстані (зміщення)\(\vecs r\) від осі, то крутний момент дорівнює поперечному добутку\(\vecs r\) і\(\vecs F: \vecs τ=\vecs r×\vecs F.\)
Ключові рівняння
- Перехресний добуток двох векторів через одиничні вектори
\[\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \]
Глосарій
перехресний продукт
\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k},\)де\(\vecs u=⟨u_1,u_2,u_3⟩\) і\(\vecs v=⟨v_1,v_2,v_3⟩\)
визначник
дійсне число, пов'язане з квадратною матрицею
паралелепіпед
тривимірна призма з шістьма гранями, які є паралелограмами
крутний момент
ефект сили, яка викликає об'єкт, щоб обертатися
потрійний скалярний добуток
крапковий добуток вектора з перехресним добутком двох інших векторів:\(\vecs u⋅(\vecs v×\vecs w)\)
вектор добуток
перехресний добуток двох векторів
