8.3: Роздільні рівняння

Цілі навчання

• Використовуйте поділ змінних для вирішення диференціального рівняння.
• Вирішувати додатки, використовуючи поділ змінних.

Зараз розглядається метод розв'язку для пошуку точних розв'язків класу диференціальних рівнянь, відомих як роздільні диференціальні рівняння. Ці рівняння поширені в самих різних дисциплін, включаючи фізику, хімію та інженерію. Ми ілюструємо кілька додатків в кінці розділу.

Поділ змінних

Почнемо з визначення та деяких прикладів.

Визначення: Роздільні диференціальні рівняння

Роздільне диференціальне рівняння - це будь-яке рівняння, яке можна записати у вигляді

$$y'=f(x)g(y). \label{sep}$$

Термін «роздільний» відноситься до того факту, що права частина Equation\ ref {sep} може бути розділена на функцію$x$ часу функції$y$. Приклади роздільних диференціальних рівнянь включають

$$\begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align}$$

Рівняння\ ref {eq2} відокремлюється з$f(x)=6x^2+4x$ і$g(y)=1$, Рівняння\ ref {eq3} відокремлюється$f(x)=1$$g(y)=\sec y+\tan y,$ і права частина рівняння\ ref {eq4} може бути врахована як$(x+3)(y−2)$, тому вона також відокремлена. Рівняння\ ref {eq3} також називають автономним диференціальним рівнянням, оскільки права частина рівняння є функцією$y$ однієї. Якщо диференціальне рівняння роздільне, то вирішити рівняння можна за допомогою методу поділу змінних.

Стратегія вирішення проблем: поділ змінних

1. Перевірте наявність будь-яких значень$y$, які роблять$g(y)=0.$ Вони відповідають постійним рішенням.
2. Перепишіть диференціальне рівняння у вигляді $$\dfrac{dy}{g(y)}=f(x)dx. \nonumber$$
3. Інтегруйте обидві сторони рівняння.
4. Вирішіть отримане рівняння для,$y$ якщо це можливо.
5. Якщо існує початкова умова, підставити відповідні значення для$x$ і$y$ в рівняння і вирішити для константи.

Зверніть увагу, що в кроці 4 зазначено «Вирішіть отримане рівняння,$y$ якщо це можливо». Не завжди вдається отримати$y$ як явну функцію$x$. Досить часто нам доводиться задовольнятися знаходженням y як неявної функції$x$.

Приклад$\PageIndex{1}$: Using Separation of Variables

Знайти загальний розв'язок диференціального рівняння$y'=(x^2−4)(3y+2)$ за допомогою методу поділу змінних.

Рішення

Дотримуйтесь п'ятикрокового методу поділу змінних.

1. У цьому прикладі$f(x)=x^2−4$ і$g(y)=3y+2$. Налаштування$g(y)=0$ дає$y=−\dfrac{2}{3}$ як постійне рішення.

2. Перепишіть диференціальне рівняння у вигляді

$$\dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber$$

3. Інтегруйте обидві сторони рівняння:

$$∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber$$

Нехай$u=3y+2$. Потім$du=3\dfrac{dy}{dx}\,dx$, таким чином рівняння стає

$$\dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber$$

$$\dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber$$

$$\dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber$$

4. Щоб вирішити це рівняння для$y$, спочатку помножте обидві сторони рівняння на$3$.

$$\ln|3y+2|=x^3−12x+3C\nonumber$$

Тепер ми використовуємо деяку логіку в роботі з константою$C$. Так як$C$ являє собою довільну константу,$3C$ також являє собою довільну константу. Якщо ми називаємо другу довільну$C_1 = 3C,$ константу$C_1,$, де рівняння стає

$$\ln|3y+2|=x^3−12x+C_1.\nonumber$$

Тепер експонентіруйте обидві сторони рівняння (тобто зробіть кожну сторону рівняння показником для основи$e$).

$$\begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}$$

Знову визначте нову константу$C_2= e^{C_1}$ (зауважте, що$C_2 > 0$):

$$|3y+2|=C_2e^{x^3−12x}.\nonumber$$

Через абсолютного значення в лівій частині рівняння це відповідає двом окремим рівнянням:

$$3y+2=C_2e^{x^3−12x}\nonumber$$

і

$$3y+2=−C_2e^{x^3−12x}.\nonumber$$

Рішення будь-якого рівняння можна записати у вигляді

$$y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber$$

Так як$C_2>0$, не має значення, чи використовуємо ми плюс або мінус, тому константа може насправді мати будь-який знак. Крім того, індекс на константі$C$ є абсолютно довільним і може бути скинутий. Тому рішення можна записати як

$$y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber$$

Зверніть увагу, що при написанні єдиного загального рішення таким чином ми також дозволяємо$C$ рівнятися$0$. Це дає нам сингулярний розв'язок для даного диференціального рівняння.$y = -\dfrac{2}{3}$ Переконайтеся, що це дійсно рішення цього диференціального рівняння!

5. Ніякої початкової умови не накладається, тому ми закінчили.

Вправа$\PageIndex{1}$

Використовувати метод поділу змінних для пошуку загального розв'язку диференціального рівняння

$$y'=2xy+3y−4x−6. \nonumber$$

Підказка

Спочатку множник правої частини рівняння шляхом групування, потім використовуйте п'ятиступінчасту стратегію поділу змінних.

Відповідь

$$y=2+Ce^{x^2+3x} \nonumber$$

Приклад$\PageIndex{2}$: Solving an Initial-Value Problem

Використовуючи метод поділу змінних, розв'яжіть початково-значну задачу

$$y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber$$

Рішення

Дотримуйтесь п'ятикрокового методу поділу змінних.

1. У цьому прикладі$f(x)=2x+3$ і$g(y)=y^2−4$. Налаштування$g(y)=0$ дає$y=±2$ як постійні рішення.

2. Розділіть обидві сторони рівняння на$y^2−4$ і помножте на$dx$. Це дає рівняння

$$\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber$$

3. Далі інтегруйте обидві сторони:

$$∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2}$$

Для оцінки лівої сторони використовують метод розкладання часткових дробів. Це призводить до ідентичності

$$\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber$$

Тоді рівняння\ ref {Ex2.2} стає

$$\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber$$

$$\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber$$

Множення обох сторін цього рівняння на$4$ і$4C$ заміна на$C_1$ дає

$$\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber$$

$$\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber$$

4. Можна розв'язати це рівняння для$y.$ First експоненти обидві сторони рівняння та визначити$C_2=e^{C_1}$:

$$\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber$$

Далі ми можемо видалити абсолютне значення і нехай нова константа$C_3$ буде позитивною, від'ємною або нульовою, тобто,$C_3 =\pm C_2$ або$C_3 = 0.$

Потім помножте обидві сторони на$y+2$.

$$y−2=C_3(y+2)e^{4x^2+12x}\nonumber$$

$$y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber$$

Тепер зберіть всі терміни, що беруть участь$y$ на одній стороні рівняння, і вирішіть для$y$:

$$y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber$$

$$y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber$$

$$y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber$$

5. Визначити значення$C_3$, підставити$x=0$ і$y=−1$ в загальне рішення. Крім того, ми можемо поставити ті самі значення в більш раннє рівняння, а саме рівняння$\dfrac{y−2}{y+2}=C_3e^{4x^2+12}$. Це набагато простіше вирішити для$C_3$:

$$\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber$$

$$\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber$$

$$C_3=−3.\nonumber$$

Тому вирішенням початкової задачі є

$$y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber$$

Графік цього рішення відображається на рисунку$\PageIndex{1}$.

Рисунок$\PageIndex{1}$: Графік розв'язку початкової задачі$y'=(2x+3)(y^2−4),y(0)=−1$.

Вправа$\PageIndex{2}$

Пошук розв'язку початкової задачі

$$6y'=(2x+1)(y^2−2y−8) \nonumber$$

з$y(0)=−3$ використанням методу поділу змінних.

Підказка

Виконайте кроки для поділу змінних, щоб вирішити початкову задачу.

Відповідь

$$y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber$$

Застосування поділу змінних

Багато цікавих завдань можна описати роздільними рівняннями. Проілюструється два типи задач: концентрації розв'язків та закон охолодження Ньютона.

Концентрації розчину

Розглянемо ємність, наповнену сольовим розчином. Ми хотіли б визначити кількість солі, присутньої в резервуарі, як функція часу. Ми можемо застосувати процес поділу змінних для вирішення цієї задачі та подібних задач, пов'язаних з концентраціями розв'язків.

Приклад$\PageIndex{3}$: Determining Salt Concentration over Time

Ємність, що містить$100$ L розчину розсолу, спочатку має$4$ кг солі, розчиненої в розчині. За часом$t=0$ в ємність надходить інший розсоляний розчин зі швидкістю$2$ л/хв. Цей розсоляний розчин містить концентрацію$0.5$ кг/л солі. При цьому на дні ємності відкривається запірний кран, що дозволяє комбінованому розчину витікати зі швидкістю$2$ л/хв, завдяки чому рівень рідини в баку залишається постійним (рис.$\PageIndex{2}$). Знайдіть кількість солі в резервуарі в залежності від часу (вимірюється в хвилинах), і знайдіть граничну кількість солі в ємності, припускаючи, що розчин в ємності добре перемішується в усі часи.

Малюнок$\PageIndex{2}$: Резервуар для розсолу з початковою кількістю розчину солі приймає вхідний потік і подає вихідний потік. Як змінюється кількість солі з часом?

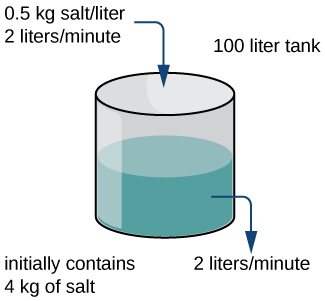
Рішення

Спочатку ми визначаємо функцію$u(t)$, яка представляє кількість солі в кілограмах в резервуарі як функцію часу. Потім$\dfrac{du}{dt}$ являє собою швидкість, з якою кількість солі в резервуарі змінюється в залежності від часу. Також,$u(0)$ являє собою кількість солі в ємності на час$t=0$, яке становить$4$ кілограми.

Загальна установка для диференціального рівняння, яке ми будемо вирішувати, має вигляд

$$\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber$$

ШВИДКІСТЬ ПРИПЛИВУ являє собою швидкість, з якою сіль надходить в резервуар, а ШВИДКІСТЬ ВІДТОКУ являє собою швидкість, з якою сіль виходить з ємності. Оскільки розчин надходить в бак зі швидкістю$2$ л/хв, а кожен літр розчину містить$0.5$ кілограм солі, щохвилини$2(0.5)=1$ кілограм солі надходить в ємність. Тому ШВИДКІСТЬ ПРИПЛИВУ =$1$.

Щоб розрахувати швидкість, з якою сіль виходить з ємності, нам потрібна концентрація солі в ємності в будь-який момент часу. Оскільки фактична кількість солі змінюється з часом, так само і концентрація солі. Однак обсяг розчину залишається фіксованим на рівні 100 літрів. Кількість кілограмів солі в ємності за часом$t$ дорівнює$u(t)$. Таким чином, концентрація солі становить$\dfrac{u(t)}{100}$ кг/л, а розчин виходить з ємності зі швидкістю$2$ л/хв. Тому сіль виходить з ємності зі швидкістю$\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}$ кг/хв, а ШВИДКІСТЬ ВІДТОКУ дорівнює$\dfrac{u(t)}{50}$. Тому диференціальне рівняння стає$\dfrac{du}{dt}=1−\dfrac{u}{50}$, а початкова умова -$u(0)=4.$ Початкова задача, яку потрібно розв'язати, є

$$\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber$$

Диференціальне рівняння є роздільним рівнянням, тому ми можемо застосувати п'ятиступінчасту стратегію для розв'язання.

Крок 1. Налаштування$1−\dfrac{u}{50}=0$ дає$u=50$ як постійне рішення. Так як початкова кількість солі в ємності становить$4$ кілограми, цей розчин не застосовується.

Крок 2. Перепишіть рівняння як

$$\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber$$

Потім помножте обидві сторони на$dt$ і розділіть обидві сторони на$50−u:$

$$\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber$$

Крок 3. Інтегруйте обидві сторони:

$$\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}$$

Крок 4. Вирішити для$u(t)$:

$$\ln|50−u|=−\dfrac{t}{50}−C\nonumber$$

$$e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber$$

$$|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber$$

Усуньте абсолютне значення, дозволивши константі бути позитивним, негативним або нульовим, тобто,$C_1 = \pm e^{-C}$ або$C_1 = 0$:

$$50−u=C_1e^{−t/50}.\nonumber$$

Нарешті, вирішуйте для$u(t)$:

$$u(t)=50−C_1e^{−t/50}.\nonumber$$

Крок 5. Вирішити для$C_1$:

$$\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}$$

Рішення початкової задачі значення полягає$u(t)=50−46e^{−t/50}.$ в тому, щоб знайти граничну кількість солі в резервуарі, візьміть межу, як$t$ наближається нескінченність:

$$\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}$$

Зауважте, що це був постійний розв'язок диференціального рівняння. Якщо початкова кількість солі в ємності$50$ кілограм, то воно залишається постійним. Якщо вона починається з менш ніж$50$ кілограмів, то вона з часом наближається до$50$ кілограмів.

Вправа$\PageIndex{3}$

Ємність містить$3$ кілограми солі, розчиненої в$75$ літрах води. Сольовий розчин$0.4$ кг солі/л перекачується в ємність зі швидкістю$6$ л/хв і зливається з такою ж швидкістю. Вирішити для концентрації солі на час$t$. Припустимо, що бак добре перемішується в усі часи.

Підказка

Дотримуйтесь інструкцій у$\PageIndex{3}$ прикладі та визначте вираз для припливу та відтоку. Сформулюйте початково-ціннісну задачу, а потім вирішуйте її.

Початкове значення задачі:

$$\dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber$$

Відповідь

$$u(t)=30−27e^{−t/50} \nonumber$$

Закон Ньютона про охолодження

Закон охолодження Ньютона стверджує, що швидкість зміни температури об'єкта пропорційна різниці між його власною температурою і температурою навколишнього середовища (тобто температурі його оточення). Якщо ми дозволимо$T(t)$ представляти температуру об'єкта як функцію часу, то$\dfrac{dT}{dt}$ представляє швидкість, з якою ця температура змінюється. Температура оточення об'єкта може бути представлена$T_s$. Тоді закон Ньютона охолодження можна записати у вигляді

$$\dfrac{dT}{dt}=k(T(t)−T_s) \nonumber$$

або просто

$$\dfrac{dT}{dt}=k(T−T_s). \nonumber$$

Температура об'єкта на початку будь-якого експерименту є початковим значенням для початкової задачі. Ми називаємо цю температуру$T_0$. Тому початково-значуща задача, яку потрібно вирішити, набуває вигляду

$$\dfrac{dT}{dt}=k(T−T_s) \label{newton}$$

з$T(0)=T_0$,$k$ де константа, яку потрібно або дати, або визначити в контексті проблеми. Ми використовуємо ці рівняння в прикладі$\PageIndex{4}$.

Приклад$\PageIndex{4}$: Waiting for a Pizza to Cool

А піца виймається з духовки після ретельно випікання, а температура духовки - Температура кухні є$75°F$, а через$5$ хвилини температура піци$340°F$.$350°F.$ Ми хотіли б дочекатися, поки температура піци досягне,$300°F$ перш ніж обробляти і подавати її (рис.$\PageIndex{3}$). Скільки ще нам доведеться чекати?

Малюнок$\PageIndex{3}$: З закону Ньютона охолодження, якщо піца остигає$10°F$ за$5$ лічені хвилини, як довго до того, як вона охолоне$300°F$?

Рішення

Температура навколишнього середовища (навколишня температура) є$75°F$, так$T_s=75$. Температура піци при її виході з духовки дорівнює$350°F$, яка є початковою температурою (тобто початковим значенням), так$T_0=350$. Тому рівняння\ ref {Ньютон} стає

$$\dfrac{dT}{dt}=k(T−75) \nonumber$$

з$T(0)=350.$

Для розв'язання диференціального рівняння використовується п'ятиступінчаста методика розв'язання роздільних рівнянь.

1. Установка правого боку дорівнює нулю дає$T=75$ як постійне рішення. Оскільки піца починається з$350°F,$ цього не рішення, яке ми шукаємо.

2. Перепишіть диференціальне рівняння, помноживши обидві сторони на$dt$ і розділивши обидві сторони на$T−75$:

$$\dfrac{dT}{T−75}=k\,dt. \nonumber$$

3. Інтегруйте обидві сторони:

$$\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber$$

4. Вирішіть для$T$, спочатку збільшивши обидві сторони:

$$\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber$$

5. Вирішити для$C$, використовуючи початкову умову$T(0)=350:$

$$\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber$$

Тому вирішенням початкової задачі є

$$T(t)=75+275e^{kt}.\nonumber$$

Щоб визначити значення$k$, нам потрібно використовувати той факт, що через$5$ хвилини температура піци буде$340°F$. Тому$T(5)=340.$ підставляючи цю інформацію в розв'язку початково-значущої задачі, ми маємо

$$T(t)=75+275e^{kt}\nonumber$$

$$T(5)=340=75+275e^{5k}\nonumber$$

$$265=275e^{5k}\nonumber$$

$$e^{5k}=\dfrac{53}{55}\nonumber$$

$$\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber$$

$$5k=\ln(\dfrac{53}{55})\nonumber$$

$$k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber$$

Отже, тепер у нас є$T(t)=75+275e^{−0.007048t}.$ Коли температура$300°F$? Рішення для$t,$ знаходимо

$$T(t)=75+275e^{−0.007048t}\nonumber$$

$$300=75+275e^{−0.007048t}\nonumber$$

$$225=275e^{−0.007048t}\nonumber$$

$$e^{−0.007048t}=\dfrac{9}{11}\nonumber$$

$$\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber$$

$$−0.007048t=\ln\dfrac{9}{11}\nonumber$$

$$t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber$$

Тому потрібно почекати додаткові$23.5$ хвилини (після того, як температура піци досягла$340°F$). Це повинно бути достатньо часу, щоб закінчити цей розрахунок.

Вправа$\PageIndex{4}$

Пиріг виймається з духовки після ретельного випікання, а температура духовки -$450°F$. Температура кухні є$70°F$, а через$10$ хвилини температура пирога$430°F$.

1. Напишіть відповідну задачу початкового значення, щоб описати цю ситуацію.
2. Вирішити початкове значення задачі для$T(t)$.
3. Скільки часу пройде, поки температура пирога не буде в межах$5°F$ кімнатної температури?

Підказка

Визначте значення,$T_s$ а$T_0$ потім скористайтеся Equation\ ref {Ньютон}.

Відповідь на

Проблема початкового значення $$\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber$$

Відповідь б

$$T(t)=70+380e^{kt}\nonumber$$

Відповідь c

Приблизно$114$ хвилин.

Ключові концепції

• Роздільне диференціальне рівняння - це будь-яке рівняння, яке можна записати у вигляді$y'=f(x)g(y).$
• Метод поділу змінних використовується для пошуку загального розв'язку відокремлюваного диференціального рівняння.

Ключові рівняння

• Роздільне диференціальне рівняння

$y′=f(x)g(y)$

• Концентрація розчину

$\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}$

• Закон Ньютона охолодження

$\dfrac{dT}{dt}=k(T−T_s)$

Глосарій

автономне диференційне рівняння

рівняння, в якому права сторона є функцією$y$ поодинці

роздільне диференціальне рівняння

будь-яке рівняння, яке можна записати у вигляді$y'=f(x)g(y)$

поділ змінних

метод, який використовується для розв'язання роздільного диференціального рівняння