8.4: Логістичне рівняння
- Page ID
- 61937
- Охарактеризуйте поняття екологічної несучої спроможності в логістичній моделі приросту населення.
- Намалюйте поле напряму для логістичного рівняння та інтерпретуйте криві розв'язку.
- Розв'яжіть логістичне рівняння та інтерпретуйте результати.
Диференціальні рівняння можуть бути використані для представлення розміру популяції, оскільки вона змінюється з часом. Ми бачили це в попередньому розділі в розділі про експоненціальне зростання і занепад, який є найпростішою моделлю. Більш реалістична модель включає в себе інші фактори, що впливають на зростання населення. У цьому розділі ми вивчаємо логістичне диференціальне рівняння і подивимося, як воно застосовується до вивчення динаміки популяцій в контексті біології.
Зростання населення та вантажопідйомність
Для моделювання зростання чисельності населення за допомогою диференціального рівняння спочатку потрібно ввести деякі змінні та відповідні терміни. Змінна\(t\). буде представляти час. Одиницями часу можуть бути години, дні, тижні, місяці або навіть роки. Будь-яка задана проблема повинна вказувати одиниці, які використовуються в цій конкретній задачі. Змінна\(P\) буде представляти сукупність. Оскільки чисельність населення змінюється з часом, це розуміється як функція часу. Тому ми використовуємо позначення\(P(t)\) для населення як функцію часу. Якщо\(P(t)\) є диференційованою функцією, то перша похідна\(\frac{dP}{dt}\) представляє миттєву швидкість зміни популяції як функцію часу.
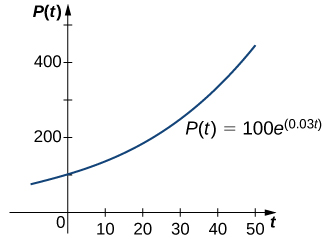
У експоненціальному зростанні та розпаді ми вивчали експоненціальний ріст і розпад популяцій та радіоактивних речовин. Прикладом експоненціальної функції зростання є\(P(t)=P_0e^{rt}.\) У цій функції,\(P(t)\) представляє населення в час\(t,P_0\) представляє початкову популяцію (популяцію в часі\(t=0\)), а константа\(r>0\) називається темпом зростання. На\(\PageIndex{1}\) малюнку зображений графік\(P(t)=100e^{0.03t}\). Ось\(P_0=100\) і\(r=0.03\).
Ми можемо перевірити, що функція\(P(t)=P_0e^{rt}\) задовольняє задачу початкового значення
\[ \dfrac{dP}{dt}=rP \nonumber \]
з\(P(0)=P_0.\)
Це диференціальне рівняння має цікаву інтерпретацію. Ліва сторона представляє швидкість, з якою чисельність населення збільшується (або зменшується). Права частина дорівнює позитивній константі, помноженої на поточну чисельність населення. Тому диференціальне рівняння стверджує, що швидкість збільшення чисельності населення пропорційна населенню на той момент часу. Крім того, він стверджує, що константа пропорційності ніколи не змінюється.
Однією з проблем цієї функції є її прогнозування того, що з часом населення зростає без обмежень. Це нереально в реальних умовах. Різні фактори обмежують темпи зростання конкретної популяції, включаючи народжуваність, смертність, запас їжі, хижаків і так далі. Константа зростання\(r\) зазвичай враховує рівень народжуваності та смертності, але жоден з інших факторів, і її можна інтерпретувати як чистий (народження мінус смерть) відсоток зростання за одиницю часу. Природне питання, яке слід задати, полягає в тому, чи темп зростання населення залишається постійним, чи змінюється він з часом. Біологи встановили, що в багатьох біологічних системах популяція зростає до досягнення певної стійкої популяції. Ця можливість не враховується при експоненціальному зростанні. Однак концепція вантажопідйомності допускає можливість того, що в даній місцевості лише певна кількість даного організму чи тварини може процвітати, не стикаючись з проблемами ресурсів.
Несуча здатність організму в даному середовищі визначається як максимальна популяція цього організму, яку навколишнє середовище може підтримувати нескінченно довго.
Використовуємо змінну\(K\) для позначення вантажопідйомності. Швидкість зростання представлена змінною\(r\). Використовуючи ці змінні, ми можемо визначити логістичне диференціальне рівняння.
\(K\)Дозволяти представляти несучу здатність для конкретного організму в даному середовищі, і нехай\(r\) буде дійсне число, яке представляє швидкість росту. Функція\(P(t)\) представляє популяцію цього організму як функцію часу\(t\), а константа\(P_0\) представляє початкову популяцію (популяцію організму в часі\(t=0\)). Тоді логістичне диференціальне рівняння
\[\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right). \label{LogisticDiffEq} \]
Логістичне рівняння було вперше опубліковано П'єром Верхульстом в\(1845\). Це диференціальне рівняння може бути пов'язане з початковою умовою\(P(0)=P_0\) для формування початкової задачі для\(P(t).\)
Припустимо, що початкова популяція невелика щодо вантажопідйомності. Тоді\(\frac{P}{K}\) невеликий, можливо, близький до нуля. Таким чином, кількість в дужках у правій частині Equation\ ref {LogisticDiffeQ} близька до\(1\), а права частина цього рівняння близька до\(rP\). Якщо\(r>0\), то популяція швидко зростає, нагадуючи експоненціальне зростання.
Однак у міру зростання населення співвідношення\(\frac{P}{K}\) також зростає, тому що\(K\) є постійним. Якщо чисельність населення залишається нижче вантажопідйомності,\(\frac{P}{K}\) то менше\(1\), значить\(1−\frac{P}{K}>0\). Тому права частина Equation\ ref {LogisticDiffeQ} все ще позитивна, але кількість в дужках стає меншою, і в результаті швидкість зростання зменшується. Якщо\(P=K\) тоді права сторона дорівнює нулю, а чисельність населення не змінюється.
Тепер припустимо, що населення починається з величини, що перевищує вантажопідйомність. Потім\(\frac{P}{K}>1,\) і\(1−\frac{P}{K}<0\). Тоді права частина Equation\ ref {LogisticDiffeq} від'ємна, а сукупність зменшується. Поки\(P>K\) чисельність населення зменшується. Він ніколи насправді не досягає K, тому що\(\frac{dP}{dt}\) стане все менше і менше, але населення наближається до вантажопідйомності, коли\(t\) наближається до нескінченності. Цей аналіз може бути представлений візуально за допомогою фазової лінії. Фазова лінія описує загальну поведінку розв'язку автономного диференціального рівняння в залежності від початкової умови. Для випадку вантажопідйомності в логістичному рівнянні фазова лінія така, як показано на малюнку\(\PageIndex{2}\).
Ця фазова лінія показує,\(P\) що коли менше нуля або більше\(K\), чисельність населення зменшується з часом. Коли\(P\) знаходиться між\(0\) і\(K\), населення збільшується з часом.
Розглянемо популяцію білохвостих оленів (Odocoileus virginianus) в штаті Кентуккі. Департамент рибних та диких ресурсів штату Кентуккі (KDFWR) встановлює керівні принципи для полювання та риболовлі в штаті. До сезону полювання 2004 року він оцінював популяцію в 900 000 оленів. Джонсон зазначає: «Популяція оленів, яка має багато їжі і на яку не полюють люди чи інші хижаки, подвоюється кожні три роки». (Джордж Джонсон, «Проблема вибуху популяції оленів не має привабливих рішень», 12 січня 2001, доступ 9 квітня 2015)

Це спостереження відповідає темпам збільшення,\(r=\dfrac{\ln (2)}{3}=0.2311,\) тому приблизний темп зростання становить 23,11% на рік. (Це передбачає, що популяція зростає експоненціально, що є розумним - принаймні в короткостроковій перспективі - з рясним запасом їжі та відсутністю хижаків.) KDFWR також повідомляє про щільність популяції оленів для 32 округів Кентуккі, середня з яких становить приблизно 27 оленів на квадратну милю. Припустимо, це щільність оленів для всієї держави (39,732 квадратних миль). \(K\)Вантажопідйомність 39,732 квадратних миль разів 27 оленів на квадратну милю, або 1,072,764 оленів.
- Для цього додатка ми маємо\(P_0=900,000,K=1,072,764,\) і\(r=0.2311.\) підставимо ці значення в Equation\ ref {LogisticDiffeQ} і формуємо задачу початкового значення.
- Вирішити задачу початкового значення з частини a.
- Згідно з цією моделлю, яким буде населення в\(3\) роках? Нагадаємо, що час подвоєння, передбачене Джонсоном для популяції оленів, становило\(3\) роки. Як порівнюються ці значення?
Припустимо, населенню вдалося досягти 1,200,000 Що прогнозує логістичне рівняння, відбудеться з населенням за цим сценарієм?
Рішення
а Початкова задача значення:
\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right),\,\,P(0)=900,000. \nonumber \]
б Логістичне рівняння є автономним диференціальним рівнянням, тому ми можемо використовувати метод поділу змінних.
Крок 1: Установка правого боку дорівнює нулю дає\(P=0\) і\(P=1,072,764.\) Це означає, що якщо населення починається з нуля, воно ніколи не зміниться, а якщо воно починається з вантажопідйомності, воно ніколи не зміниться.
Крок 2: Перепишіть диференціальне рівняння і помножте обидві сторони на:
\[ \begin{align*} \dfrac{dP}{dt} =0.2311P\left(\dfrac{1,072,764−P}{1,072,764} \right) \\[4pt] dP =0.2311P\left(\dfrac{1,072,764−P}{1,072,764}\right)dt \\[4pt] \dfrac{dP}{P(1,072,764−P)} =\dfrac{0.2311}{1,072,764}dt. \end{align*}\]
Крок 3: Інтегруйте обидві сторони рівняння, використовуючи розкладання часткових дробів:
\[ \begin{align*} ∫\dfrac{dP}{P(1,072,764−P)} =∫\dfrac{0.2311}{1,072,764}dt \\[4pt] \dfrac{1}{1,072,764}∫ \left(\dfrac{1}{P}+\dfrac{1}{1,072,764−P}\right)dP =\dfrac{0.2311t}{1,072,764}+C \\[4pt] \dfrac{1}{1,072,764}\left(\ln |P|−\ln |1,072,764−P|\right) =\dfrac{0.2311t}{1,072,764}+C. \end{align*} \nonumber \]
Крок 4: Помножте обидві сторони на 1,072,764 і використовуйте часткове правило для логарифмів:
\[\ln \left|\dfrac{P}{1,072,764−P}\right|=0.2311t+C_1. \nonumber \]
Тут\(C_1=1,072,764C.\) Next експонентірует обидві сторони і усуває абсолютне значення:
\[ \begin{align*} e^{\ln \left|\dfrac{P}{1,072,764−P} \right|} =e^{0.2311t + C_1} \\[4pt] \left|\dfrac{P}{1,072,764 - P}\right| =C_2e^{0.2311t} \\[4pt] \dfrac{P}{1,072,764−P} =C_2e^{0.2311t}. \end{align*}\]
Тут\(C_2=e^{C_1}\), але після усунення абсолютного значення, воно також може бути негативним. Тепер вирішуйте для:
\[ \begin{align*} P =C_2e^{0.2311t}(1,072,764−P) \\[4pt] P =1,072,764C_2e^{0.2311t}−C_2Pe^{0.2311t} \\[4pt] P + C_2Pe^{0.2311t} = 1,072,764C_2e^{0.2311t} \\[4pt] P(1+C_2e^{0.2311t} =1,072,764C_2e^{0.2311t} \\[4pt] P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.23\nonumber11t}}. \end{align*}\]
Крок 5: Щоб визначити значення\(C_2\), насправді простіше повернутися на пару кроків туди, де\(C_2\) було визначено. Зокрема, використовують рівняння
\[\dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]
Початкова умова є\(P(0)=900,000\). \(P\)Замініть на\(900,000\) і\(t\) на нуль:
\[ \begin{align*} \dfrac{P}{1,072,764−P} =C_2e^{0.2311t} \\[4pt] \dfrac{900,000}{1,072,764−900,000} =C_2e^{0.2311(0)} \\[4pt] \dfrac{900,000}{172,764} =C_2 \\[4pt] C_2 =\dfrac{25,000}{4,799} \\[4pt] ≈5.209. \end{align*}\]
Тому
\[ \begin{align*} P(t) =\dfrac{1,072,764 \left(\dfrac{25000}{4799}\right)e^{0.2311t}}{1+(250004799)e^{0.2311t}}\\[4pt] =\dfrac{1,072,764(25000)e^{0.2311t}}{4799+25000e^{0.2311t}.} \end{align*}\]
Ділення чисельника і знаменника на 25 000 дає
\[P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]
Малюнок - це графік цього рівняння.
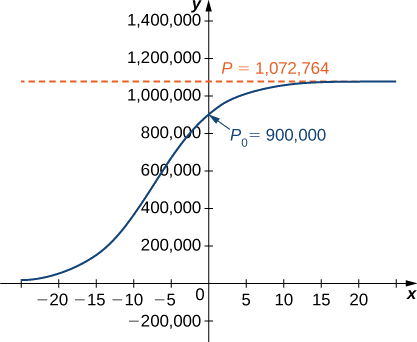
c Використовуючи цю модель, ми можемо спрогнозувати чисельність населення через 3 роки.
\[P(3)=\dfrac{1,072,764e^{0.2311(3)}}{0.19196+e^{0.2311(3)}}≈978,830\,deer \nonumber \]
Це далеко не вдвічі перевищує початкове населення\(900,000.\) Пам'ятайте, що час подвоєння ґрунтується на припущенні, що темпи зростання ніколи не змінюються, але логістична модель враховує цю можливість.
d Якби популяція досягла 1 200 000 оленів, то нова проблема початкового значення була б
\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right), \, P(0)=1,200,000. \nonumber \]
Загальне рішення диференціального рівняння залишилося б тим самим.
\[ P(t)=\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \nonumber \]
Щоб визначити значення константи, поверніться до рівняння
\[ \dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]
Підставляючи значення,\(t=0\) і\(P=1,200,000,\) ви отримаєте
\[ \begin{align*} C_2e^{0.2311(0)} =\dfrac{1,200,000}{1,072,764−1,200,000} \\[4pt] C_2 =−\dfrac{100,000}{10,603}≈−9.431.\end{align*}\]
Тому
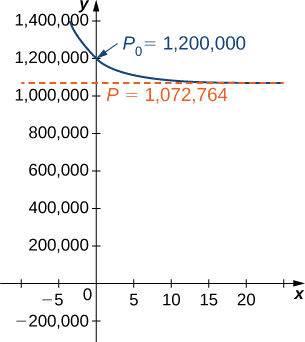
\[ \begin{align*} P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \\[4pt] =\dfrac{1,072,764 \left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}}{1+\left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}} \\[4pt] =−\dfrac{107,276,400,000e^{0.2311t}}{100,000e^{0.2311t}−10,603} \\[4pt] ≈\dfrac{10,117,551e^{0.2311t}}{9.43129e^{0.2311t}−1} \end{align*}\]
Це рівняння зображено на малюнку\(\PageIndex{5}\).
Розв'язування логістичного диференціального рів
Логістичне диференціальне рівняння є автономним диференціальним рівнянням, тому ми можемо використовувати розділення змінних, щоб знайти загальне рішення, як ми тільки що зробили в прикладі\(\PageIndex{1}\).
Крок 1: Встановлення правої сторони, рівної нулю, призводить до\(P=0\) і\(P=K\) як постійних рішень. Перше рішення вказує на те, що коли немає організмів, популяція ніколи не буде рости. Друге рішення вказує на те, що коли населення почне з вантажопідйомності, вона ніколи не зміниться.
Крок 2: Перепишіть диференціальне рівняння у вигляді
\[ \dfrac{dP}{dt}=\dfrac{rP(K−P)}{K}. \nonumber \]
Потім помножте обидві сторони на\(dt\) і розділіть обидві сторони на\(P(K−P).\) Це призводить до
\[ \dfrac{dP}{P(K−P)}=\dfrac{r}{K}dt. \nonumber \]
Помножте обидві сторони рівняння на\(K\) та інтегруйте:
\[ ∫\dfrac{K}{P(K−P)}dP=∫rdt. \label{eq20a} \]
Ліву частину цього рівняння можна інтегрувати за допомогою розкладання часткових дробів. Ми залишаємо це вам, щоб переконатися, що
\[ \dfrac{K}{P(K−P)}=\dfrac{1}{P}+\dfrac{1}{K−P}. \nonumber \]
Тоді рівняння\ ref {eq20a} стає
\[ ∫\dfrac{1}{P}+\dfrac{1}{K−P}dP=∫rdt \nonumber \]
\[ \ln |P|−\ln |K−P|=rt+C \nonumber \]
\[ \ln ∣\dfrac{P}{K−P}∣=rt+C. \nonumber \]
Тепер експонентіровать обидві сторони рівняння, щоб усунути натуральний логарифм:
\[ e^{\ln ∣\dfrac{P}{K−P}∣}=e^{rt+C} \nonumber \]
\[ ∣\dfrac{P}{K−P}∣=e^Ce^{rt}. \nonumber \]
Визначаємо\(C_1=e^c\) так, щоб рівняння стало
\[ \dfrac{P}{K−P}=C_1e^{rt}. \label{eq30a} \]
Щоб вирішити це рівняння для\(P(t)\), спочатку помножте обидві сторони на\(K−P\) і зберіть члени, що\(P\) містяться в лівій частині рівняння:
\[\begin{align*} P =C_1e^{rt}(K−P) \\[4pt] =C_1Ke^{rt}−C_1Pe^{rt} \\[4pt] P+C_1Pe^{rt} =C_1Ke^{rt}.\end{align*}\]
Далі множник\(P\) з лівого боку і розділіть обидві сторони на інший фактор:
\[\begin{align*} P(1+C_1e^{rt}) =C_1Ke^{rt} \\[4pt] P(t) =\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}. \end{align*}\]
Останнім кроком є визначення значення\(C_1.\) Найпростіший спосіб зробити це - підставити\(t=0\) і замість\(P_0\)\(P\) в Рівняння і вирішити для\(C_1\):
\[\begin{align*} \dfrac{P}{K−P} = C_1e^{rt} \\[4pt] \dfrac{P_0}{K−P_0} =C_1e^{r(0)} \\[4pt] C_1 = \dfrac{P_0}{K−P_0}. \end{align*}\]
Нарешті,\(C_1\) підставляємо вираз для рівняння\ ref {eq30a}:
\[ P(t)=\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}=\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \nonumber \]
Тепер помножте чисельник і знаменник правої частини на\((K−P_0)\) і спростіть:
\[\begin{align*} P(t) =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \\[4pt] =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}}⋅\dfrac{K−P_0}{K−P_0} =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}. \end{align*}\]
Викладемо цей результат як теорему.
Розглянемо логістичне диференціальне рівняння з урахуванням початкової сукупності\(P_0\) з вантажопідйомністю\(K\) та темпами зростання\(r\). Розв'язок відповідної початкової задачі задається
\[P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \nonumber \].
Тепер, коли у нас є рішення початкової задачі, ми можемо вибрати значення для\(P_0,r\)\(K\) та вивчити криву розв'язку. Наприклад, у прикладі ми використовували значення\(r=0.2311,K=1,072,764,\) та початкову популяцію\(900,000\) оленів. Це призводить до вирішення
\[\begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{(1,072,764−900,000)+900,000e^{0.2311t}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{172,764+900,000e^{0.2311t}}.\end{align*}\]
Розділення верхньої і нижньої частини на\(900,000\) дає
\[ P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]
Це те ж саме, що і оригінальне рішення. Графік цього рішення знову показаний синім кольором на малюнку\(\PageIndex{6}\), накладеного на графік експоненціальної моделі зростання з початковою чисельністю населення\(900,000\) та темпами зростання\(0.2311\) (відображається зеленим кольором). Червона пунктирна лінія представляє вантажопідйомність і є горизонтальною асимптотою для розв'язку логістичного рівняння.
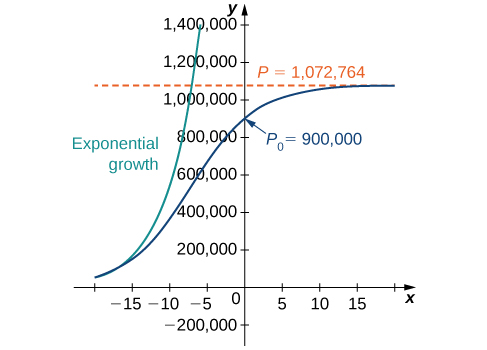
Працюючи з припущенням, що чисельність населення зростає відповідно до логістичного диференціального рівняння, цей графік прогнозує\((1984)\), що приблизно\(20\) роками раніше приріст населення був дуже близький до експоненціального. Чистий темп зростання на той час був би приблизно\(23.1%\) на рік. З плином часу два графіки розділяються. Це відбувається тому, що населення збільшується, а логістичне диференціальне рівняння стверджує, що темпи зростання зменшуються зі збільшенням населення. У той час, коли було виміряно населення\((2004)\), воно було близьке до вантажопідйомності, і населення починало вирівнюватися.
Розв'язок логістичного диференціального рівняння має точку перегину. Щоб знайти цю точку, встановіть другу похідну рівну нулю:
\[ \begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \\[4pt] P′(t) =\dfrac{rP_0K(K−P0)e^{rt}}{((K−P_0)+P_0e^{rt})^2} \\[4pt] P''(t) =\dfrac{r^2P_0K(K−P_0)^2e^{rt}−r^2P_0^2K(K−P_0)e^{2rt}}{((K−P_0)+P_0e^{rt})^3} \\[4pt] =\dfrac{r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})}{((K−P_0)+P_0e^{rt})^3}. \end{align*}\]
Встановлення чисельника, рівного нулю,
\[ r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})=0. \nonumber \]
До тих пір\(P_0≠K\), поки вся кількість до і включення\(e^{rt}\) не є нульовою, тому ми можемо розділити її:
\[ (K−P_0)−P_0e^{rt}=0. \nonumber \]
Рішення для\(t\),
\[ P_0e^{rt}=K−P_0 \nonumber \]
\[ e^{rt}=\dfrac{K−P_0}{P_0} \nonumber \]
\[ \ln e^{rt}=\ln \dfrac{K−P_0}{P_0} \nonumber \]
\[ rt=\ln \dfrac{K−P_0}{P_0} \nonumber \]
\[ t=\dfrac{1}{r}\ln \dfrac{K−P_0}{P_0}. \nonumber \]
Зверніть увагу\(P_0>K\), що якщо, то ця величина не визначена, і графік не має точки перегину. На логістичному графіку точку перегину можна розглядати як точку, де графік змінюється від увігнутого до увігнутого вниз. Тут починає відбуватися «вирівнювання», оскільки чистий темп зростання стає повільнішим, коли населення починає наближатися до пропускної здатності.
Популяція кроликів на лузі спостерігається, щоб бути\(200\) кроликами в часі\(t=0\). Через місяць спостерігається збільшення популяції кроликів на\(4%\). Використовуючи початкову популяцію\(200\) та темпи зростання\(0.04\), з вантажопідйомністю\(750\) кроликів,
- Запишіть логістичне диференціальне рівняння та початкову умову для цієї моделі.
- Намалюйте поле нахилу для цього логістичного диференціального рівняння та намалюйте рішення, відповідне початковій популяції\(200\) кроликів.
- Вирішити початкову задачу для\(P(t)\).
- Використовуйте рішення для прогнозування чисельності населення за\(1\) роком.
- Підказка
-
Спочатку визначають значення\(r,K,\) і\(P_0\). Потім створіть задачу початкового значення, намалюйте поле напряму та вирішіть проблему.
- Відповідь
-
а.\(\dfrac{dP}{dt}=0.04(1−\dfrac{P}{750}),P(0)=200\)
б.
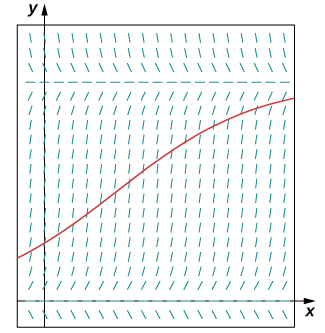
c.\(P(t)=\dfrac{3000e^{.04t}}{11+4e^{.04t}}\)
г Через\(12\) місяці популяція буде\(P(12)≈278\) кроликами.
Удосконалення логістичної моделі включає порогове населення. Порогова популяція визначається як мінімальна популяція, яка необхідна для виживання виду. Ми використовуємо змінну\(T\) для представлення порогової сукупності. Диференціальне рівняння, яке включає як порогове населення, так\(T\) і\(K\) вантажопідйомність,
\[ \dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right) \nonumber \]
де\(r\) являє собою швидкість зростання, як і раніше.
- Порогова популяція корисна біологам і може бути використана для визначення того, чи слід заносити даний вид до списку, що знаходиться під загрозою зникнення. Група австралійських дослідників стверджує, що вони визначили порогову популяцію для виживання будь-якого виду:\(5000\) дорослих. (Кетрін Клаббі, «Магічне число», американський вчений 98 (1): 24, дої:10.1511/2010.82.24. доступний 9 квітня 2015 року, www.americanscientist.org/iss... a-магічний номер). Тому ми використовуємо в\(T=5000\) якості порога населення в цьому проекті. Припустимо, що екологічна вантажопідйомність в штаті Монтана для лося є\(25,000\). Налаштуйте рівняння, використовуючи пропускну здатність\(25,000\) і порогову заселеність\(5000\). Припустимо річний чистий темп приросту 18%.
- Намалюйте поле напряму для диференціального рівняння з кроку\(1\) разом з декількома розв'язками для різних початкових популяцій. Які постійні розв'язки диференціального рівняння? Чому ці рішення відповідають в оригінальній моделі популяції (тобто в біологічному контексті)?
- Яка гранична чисельність населення для кожної вихідної популяції, яку ви обрали на крок\(2\)? (Підказка: використовуйте поле нахилу, щоб побачити, що відбувається для різних початкових груп населення, тобто шукайте горизонтальні асимптоти ваших рішень.)
- Це рівняння можна вирішити за допомогою методу поділу змінних. Однак дуже складно отримати рішення як явну функцію\(t\). Використовуючи початкову популяцію\(18,000\) лося, вирішити початкову задачу і висловити рішення як неявну функцію t, або вирішити загальну початкову задачу, знаходячи рішення з точки зору\(r,K,T,\) і\(P_0\).
Ключові концепції
- При вивченні функцій населення різні припущення, такі як експоненціальне зростання, логістичне зростання або порогове населення, призводять до різних темпів зростання.
- Логістичне диференціальне рівняння включає в себе поняття вантажопідйомності. Це значення є граничним значенням для населення для будь-якого даного середовища.
- Логістичне диференціальне рівняння може бути вирішено для будь-яких позитивних темпів зростання, початкової чисельності населення та пропускної здатності.
Ключові рівняння
- Логістичне диференціальне рівняння та початкова задача
\(\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right),\quad P(0)=P_0\)
- Розв'язок задачі логістичного диференціального рівняння/початкового значення
\(P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\)
- Модель порогової чисельності населення
\(\dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right)\)
Глосарій
- вантажопідйомність
- максимальна популяція організму, яку навколишнє середовище може підтримувати нескінченно довго
- швидкість зростання
- константа\(r>0\) в експоненціальній функції зростання\(P(t)=P_0e^{rt}\)
- початкова популяція
- населення на час\(t=0\)
- логістичний диференціальний рівнян
- диференціальне рівняння, яке включає в себе\(K\) несучу здатність і швидкість зростання rr в модель популяції
- фазова лінія
- візуальне зображення поведінки розв'язків автономного диференціального рівняння з урахуванням різних початкових умов
- поріг населення
- мінімальна популяція, яка необхідна для виживання виду
