8.1: Основи диференціальних рівнянь

Last updated
Save as PDF

Page ID: 61936

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте порядок диференціального рівняння.
Поясніть, що мається на увазі під розв'язком диференціального рівняння.
Розрізняють загальне рішення і конкретне рішення диференціального рівняння.
Визначте проблему початкового значення.
Визначте, чи є дана функція розв'язком диференціального рівняння або задачею початкового значення.

Обчислення - це математика змін, а темпи змін виражаються похідними. Таким чином, одним з найпоширеніших способів використання числення є створення рівняння, що містить невідому функцію\(y=f(x)\) та її похідну, відоме як диференціальне рівняння. Рішення таких рівнянь часто дає інформацію про те, як змінюються величини, і часто дає уявлення про те, як і чому відбуваються зміни.

Методи розв'язання диференціальних рівнянь можуть приймати безліч різних форм, включаючи пряме рішення, використання графіків або комп'ютерні обчислення. Ми представимо основні ідеї в цьому розділі і опишемо їх трохи докладніше пізніше в курсі. У цьому розділі ми вивчаємо, що таке диференціальні рівняння, як перевірити їх розв'язки, деякі методи, які використовуються для їх розв'язання, а також деякі приклади загальних і корисних рівнянь.

Загальні диференційні рівняння

Розглянемо рівняння\(y′=3x^2,\), яке є прикладом диференціального рівняння, оскільки воно включає похідну. Існує зв'язок між змінними\(x\) і\(y:y\) є невідомою функцією\(x\). Крім того, ліва частина рівняння є похідною від\(y\). Тому ми можемо інтерпретувати це рівняння наступним чином: Почніть з якоїсь функції\(y=f(x)\) і візьміть її похідну. Відповідь повинна дорівнювати\(3x^2\). Яку функцію має похідна, яка дорівнює\(3x^2\)? Однією з таких функцій є\(y=x^3\), тому ця функція вважається розв'язком диференціального рівняння.

Визначення: диференціальне рівнян

Диференціальне рівняння - це рівняння, що включає невідому функцію\(y=f(x)\) і одну або кілька її похідних. Розв'язок диференціального рівняння - це функція\(y=f(x)\), яка задовольняє диференціальному рівнянню, коли\(f\) і його похідні підставляються в рівняння.

Перейдіть на цей веб-сайт, щоб дізнатися більше про цю тему.

Деякі приклади диференціальних рівнянь та їх розв'язків наведені в табл\(\PageIndex{1}\).

Таблиця\(\PageIndex{1}\): приклади диференціальних рівнянь та їх розв'язки
Рівняння	Рішення
\(y'=2x\)	\(y=x^2\)
\(y'+3y=6x+11\)	\(y=e^{−3x}+2x+3\)
\(y''−3y'+2y=24e^{−2x}\)	\(y=3e^x−4e^{2x}+2e^{−2x}\)

Зверніть увагу, що рішення диференціального рівняння не обов'язково є унікальним, перш за все тому, що похідна константи дорівнює нулю. Наприклад, також\(y=x^2+4\) є розв'язком першого диференціального рівняння в табл\(\PageIndex{1}\). До цієї ідеї ми повернемося трохи пізніше в цьому розділі. Поки що давайте зосередимося на тому, що означає для функції, щоб бути розв'язком диференціального рівняння.

Приклад\(\PageIndex{1}\): Verifying Solutions of Differential Equations

Переконайтеся, що функція\(y=e^{−3x}+2x+3\) є розв'язком диференціального рівняння\(y′+3y=6x+11\).

Рішення

Щоб перевірити рішення, спочатку обчислюємо,\(y′\) використовуючи правило ланцюга для похідних. Це дає\(y′=−3e^{−3x}+2\). Далі підставляємо\(y\) і\(y′\) в ліву частину диференціального рівняння:

\((−3e^{−2x}+2)+3(e^{−2x}+2x+3).\)

Отриманий вираз можна спростити, попередньо розподіливши для усунення дужок, надавши

\(−3e^{−2x}+2+3e^{−2x}+6x+9.\)

Поєднання подібних термінів призводить до виразу\(6x+11\), яке дорівнює правій частині диференціального рівняння. Цей результат перевіряє, що\(y=e^{−3x}+2x+3\) є розв'язком диференціального рівняння.

Вправа\(\PageIndex{1}\)

Переконайтеся, що\(y=2e^{3x}−2x−2\) це рішення диференціального рівняння\(y′−3y=6x+4.\)

Підказка: Спочатку обчислити\(y′\) потім підставити обидва\(y′\) і\(y\) в ліву сторону.

Зручно визначати характеристики диференціальних рівнянь, які полегшують розмову про них і класифікувати їх. Найголовнішою характеристикою диференціального рівняння є його порядок.

Означення: порядок диференціального рівняння

Порядок диференціального рівняння - це найвищий порядок будь-якої похідної невідомої функції, яка фігурує в рівнянні.

Приклад\(\PageIndex{2}\): Identifying the Order of a Differential Equation

Найвища похідна в\(y′\) рівнянні -

Який порядок кожного з наступних диференціальних рівнянь?

\(y′−4y=x^2−3x+4\)
\(x^2y'''−3xy''+xy′−3y=\sin x\)
\(\frac{4}{x}y^{(4)}−\frac{6}{x^2}y''+\frac{12}{x^4}y=x^3−3x^2+4x−12\)

Рішення

Найвища похідна в рівнянні є\(y′\), тому порядок є\(1\).
Найвища похідна в рівнянні є\(y'''\), тому порядок є\(3\).
Найвища похідна в рівнянні є\(y^{(4)}\), тому порядок є\(4\).

Вправа\(\PageIndex{2}\)

Який порядок наступного диференціального рівняння?

\((x^4−3x)y^{(5)}−(3x^2+1)y′+3y=\sin x\cos x\)

Підказка: Яка найвища похідна в рівнянні?

Відповідь: \(5\)

Загальні та конкретні рішення

Ми вже відзначали, що диференціальне рівняння\(y′=2x\) має як мінімум два рішення:\(y=x^2\) і\(y=x^2+4\). Єдина відмінність цих двох рішень - останній термін, який є константою. Що робити, якщо останній термін - інша константа? Чи буде цей вираз все ще рішенням диференціального рівняння? Насправді будь-яка функція форми\(y=x^2+C\), де\(C\) представляє будь-яку константу, також є рішенням. Причина в тому, що похідна від\(x^2+C\) є\(2x\), незалежно від значення\(C\). Можна показати, що будь-який розв'язок цього диференціального рівняння повинен мати вигляд\(y=x^2+C\). Це приклад загального розв'язку диференціального рівняння. Графік деяких з цих розв'язків наведено на рис\(\PageIndex{1}\). (Примітка: у цьому графіку ми використовували парні цілі значення для C, що знаходяться між\(−4\) і\(4\). Насправді немає обмежень на значення\(C\); це може бути ціле число чи ні.)

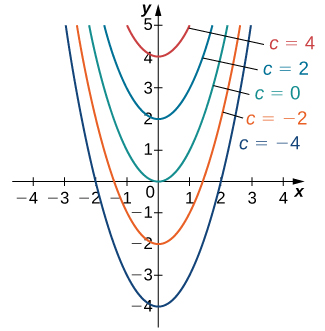
Графік сімейства розв'язків диференціального рівняння y' = 2 x, які мають вигляд y = x ^ 2 + C. Параболи наведено для значень C: -4, -2, 0, 2 і 4. — Малюнок\(\PageIndex{1}\): Сімейство розв'язків диференціального рівняння\(y′=2x.\)

У цьому прикладі ми можемо вибрати будь-яке рішення, яке ми бажаємо; наприклад,\(y=x^2−3\) є членом сімейства розв'язків цього диференціального рівняння. Це називається певним розв'язком диференціального рівняння. Конкретне рішення часто можна однозначно визначити, якщо нам нададуть додаткову інформацію про проблему.

Приклад\(\PageIndex{3}\): Finding a Particular Solution

Знайдіть конкретний розв'язок диференціального рівняння,\(y′=2x\) що проходить через точку\((2,7)\).

Рішення

Будь-яка функція виду\(y=x^2+C\) є розв'язком цього диференціального рівняння. Щоб визначити значення\(C\), підставляємо значення\(x=2\) і\(y=7\) в це рівняння і вирішуємо для\(C\):

\[ \begin{align*} y =x^2+C \\[4pt] 7 =2^2+C \\[4pt] =4+C \\[4pt] C =3. \end{align*}\]

Тому конкретне рішення, що проходить через точку\((2,7)\), є\(y=x^2+3\).

Вправа\(\PageIndex{3}\)

Знайти конкретний розв'язок диференціального рівняння

\[ y′=4x+3 \nonumber \]

проходження через\((1,7),\) задану точку, яка\(y=2x^2+3x+C\) є загальним рішенням диференціального рівняння.

Підказка: Спочатку\(y=7\) підставляємо\(x=1\) і в рівняння, потім вирішуємо для\(C\).

Відповідь: \[ y=2x^2+3x+2 \nonumber \]

Проблеми з початковим значенням

Зазвичай дане диференціальне рівняння має нескінченну кількість розв'язків, тому природно запитати, який з них ми хочемо використовувати. Щоб вибрати одне рішення, потрібно більше інформації. Деяка конкретна інформація, яка може бути корисною, - це початкове значення, яке представляє собою впорядковану пару, яка використовується для пошуку того чи іншого рішення.

Диференціальне рівняння разом з одним або декількома початковими значеннями називається початковою задачею. Загальне правило полягає в тому, що кількість початкових значень, необхідних для початкової задачі, дорівнює порядку диференціального рівняння. Наприклад, якщо у нас є диференціальне рівняння\(y′=2x\), то\(y(3)=7\) є початковим значенням, а при спільному утриманні ці рівняння утворюють початково-значну задачу. \(y''−3y′+2y=4e^x\)Диференціальне рівняння другого порядку, тому нам потрібні два початкових значення. При початкових задачах порядку більше одиниці слід використовувати те саме значення для незалежної змінної. Прикладом початкових значень для цього рівняння другого порядку буде\(y(0)=2\) і\(y′(0)=−1.\) Ці два початкові значення разом з диференціальним рівнянням утворюють початкову задачу. Ці проблеми так названі тому, що часто незалежна змінна в невідомій функції є\(t\), яка представляє час. Таким чином, значення\(t=0\) являє собою початок завдання.

Приклад\(\PageIndex{4}\): Verifying a Solution to an Initial-Value Problem

Переконайтеся, що функція\(y=2e^{−2t}+e^t\) є рішенням початкової задачі

\[ y′+2y=3e^t, \quad y(0)=3.\nonumber \]

Рішення

Щоб функція задовольняла початкову задачу, вона повинна задовольняти як диференціальне рівняння, так і початкову умову. Щоб показати, що\(y\) задовольняє диференціальне рівняння, почнемо з обчислення\(y′\). Це дає\(y′=−4e^{−2t}+e^t\). Далі підставляємо обидва\(y\) і\(y′\) в ліву частину диференціального рівняння і спрощуємо:

\[ \begin{align*} y′+2y &=(−4e^{−2t}+e^t)+2(2e^{−2t}+e^t) \\[4pt] &=−4e^{−2t}+e^t+4e^{−2t}+2e^t =3e^t. \end{align*}\]

Це дорівнює правій частині диференціального рівняння, тому\(y=2e^{−2t}+e^t\) вирішує диференціальне рівняння. Далі розраховуємо\(y(0)\):

\[ y(0)=2e^{−2(0)}+e^0=2+1=3. \nonumber \]

Цей результат перевіряє початкове значення. Тому дана функція задовольняє задачу початкового значення.

Вправа\(\PageIndex{4}\)

Переконайтеся, що\(y=3e^{2t}+4\sin t\) це рішення проблеми з початковим значенням

\[ y′−2y=4\cos t−8\sin t,y(0)=3. \nonumber \]

Підказка: Спочатку перевірте, що\(y\) вирішує диференціальне рівняння. Потім перевірте початкове значення.

У\(\PageIndex{4}\) прикладі початкова задача складалася з двох частин. Перша частина була диференціальним рівнянням\(y′+2y=3e^x\), а друга частина була початковим значенням\(y(0)=3.\) Ці два рівняння разом утворили початкову задачу.

Те ж саме вірно і в цілому. Початкова задача буде складатися з двох частин: диференціального рівняння і початкової умови. Диференціальне рівняння має сімейство розв'язків, а початкова умова визначає значення\(C\). Сімейство розв'язків диференціального рівняння у прикладі\(\PageIndex{4}\) наведено\(y=2e^{−2t}+Ce^t.\) цим сімейством розв'язків на малюнку\(\PageIndex{2}\), з\(y=2e^{−2t}+e^t\) позначенням конкретного розв'язку.

Графік сімейства розв'язків диференціального рівняння y' + 2 y = 3 e ^ t, які мають вигляд y = 2 e ^ (-2 t) + C e ^ t Показані версії з C = 1, 0,5 та -0.2, серед інших, не позначені. Для всіх значень C функція швидко зростає для t < 0, коли t переходить до від'ємної нескінченності. Для C — Рисунок\(\PageIndex{2}\): Сімейство розв'язків диференціального рівняння\(y′+2y=3e^t\). \(y=2e^{−2t}+e^t\)Конкретний розчин маркується.

Приклад\(\PageIndex{5}\): Solving an Initial-value Problem

Вирішіть наступну проблему початкового значення:

\[ y′=3e^x+x^2−4,y(0)=5. \nonumber \]

Рішення

Першим кроком у вирішенні цієї початково-ціннісної задачі є пошук загального сімейства рішень. Для цього знаходимо антипохідне обох сторін диференціального рівняння

\[∫y′\,dx=∫(3e^x+x^2−4)\,dx, \nonumber \]

а саме,

\(y+C_1=3e^x+\frac{1}{3}x^3−4x+C_2\).

Ми можемо інтегрувати обидві сторони, оскільки термін y з'являється сам по собі. Зверніть увагу, що існує дві константи інтеграції:\(C_1\) і\(C_2\). Розв'язування цього рівняння для\(y\) дає

\(y=3e^x+\frac{1}{3}x^3−4x+C_2−C_1.\)

Тому що\(C_1\) і\(C_2\) є обома константами, також\(C_2−C_1\) є постійною. Тому ми можемо визначити\(C=C_2−C_1,\), що призводить до рівняння

\(y=3e^x+\frac{1}{3}x^3−4x+C.\)

Далі визначаємо значення\(C\). Для цього підставляємо\(x=0\) і\(y=5\) в це рівняння і вирішуємо для\(C\):

\[ \begin{align*} 5 &=3e^0+\frac{1}{3}0^3−4(0)+C \\[4pt] 5 &=3+C \\[4pt] C&=2 \end{align*}. \nonumber \]

Тепер підставляємо значення\(C=2\) в загальне рівняння. Рішенням початкової задачі є\(y=3e^x+\frac{1}{3}x^3−4x+2.\)

Аналіз

Різниця між загальним рішенням і конкретним рішенням полягає в тому, що загальне рішення включає сімейство функцій, явно або неявно визначених, незалежної змінної. Початкове значення або значення визначають, який саме розчин в сімействі розчинів задовольняє бажаним умовам.

Вправа\(\PageIndex{5}\)

Вирішити задачу початкового значення

\[ y′=x^2−4x+3−6e^x,y(0)=8. \nonumber \]

Підказка: Спочатку візьміть антипохідне обох сторін диференціального рівняння. Потім\(y=8\) підставляємо\(x=0\) і в отримане рівняння і вирішуємо для\(C\).

Відповідь: \(y=\frac{1}{3}x^3−2x^2+3x−6e^x+14\)

У фізиці та інженерних додатках ми часто розглядаємо сили, що діють на об'єкт, і використовуємо цю інформацію, щоб зрозуміти результуючий рух, який може статися. Наприклад, якщо ми починаємо з об'єкта на поверхні Землі, основною силою, що діє на цей об'єкт, є гравітація. Фізики та інженери можуть використовувати цю інформацію разом із другим законом руху Ньютона (у формі рівняння\(F=ma\), де\(F\) представляє силу,\(m\) представляє масу та\(a\) представляє прискорення), щоб вивести рівняння, яке можна вирішити.

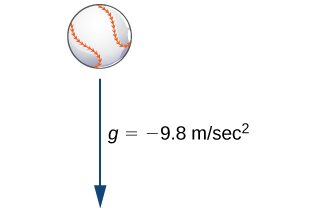
Малюнок бейсболу зі стрілкою під ним, спрямованою вниз. Стрілка позначається g = -9,8 м/сек ^ 2. — Малюнок\(\PageIndex{3}\): Для бейсболу, що падає в повітрі, єдиною силою, що діє на нього, є гравітація (нехтуючи опором повітря).

На малюнку\(\PageIndex{3}\) ми припускаємо, що єдиною силою, що діє на бейсбол, є сила тяжіння. Це припущення ігнорує опір повітря. (Сила, обумовлена опором повітря, розглядається в подальшому обговоренні.) Прискорення за рахунок гравітації на поверхні Землі, g, приблизно\(9.8\,\text{m/s}^2\). Введемо систему відліку, де поверхня Землі знаходиться на висоті 0 метрів. \(v(t)\)Дозволяти представляти швидкість об'єкта в метрах в секунду. Якщо\(v(t)>0\), м'яч піднімається, а якщо\(v(t)<0\), то м'яч падає (рис.).

Зображення бейсболу зі стрілкою над ним, спрямованою вгору, і стрілкою під нею, спрямованою вниз. Стрілка, спрямована вгору, позначається як v (t) — Малюнок\(\PageIndex{4}\): Можливі швидкості для висхідного/падіння бейсболу.

Наша мета полягає в тому, щоб вирішити швидкість\(v(t)\) в будь-який час\(t\). Для цього налаштовуємо задачу початкового значення. Припустимо, маса кульки є\(m\), де\(m\) вимірюється в кілограмах. Ми використовуємо другий закон Ньютона, який стверджує, що сила, що діє на об'єкт, дорівнює його масі, що перевищує його прискорення\((F=ma)\). Прискорення є похідною швидкості, так що\(a(t)=v′(t)\). Тому сила, що діє на бейсбол, дається\(F=mv′(t)\). Однак ця сила повинна дорівнювати силі тяжіння, що діє на об'єкт, яка (знову ж за допомогою другого закону Ньютона) дається\(F_g=−mg\), так як ця сила діє в напрямку вниз. Тому отримуємо рівняння\(F=F_g\), яке стає\(mv′(t)=−mg\). Ділення обох сторін рівняння на\(m\) дає рівняння

\[ v′(t)=−g. \nonumber \]

Зверніть увагу, що це диференціальне рівняння залишається незмінним незалежно від маси об'єкта.

Тепер нам знадобиться початкове значення. Оскільки ми вирішуємо для швидкості, має сенс в контексті задачі припустити, що ми знаємо початкову швидкість, або швидкість в часі\(t=0.\) Це позначається\(v(0)=v_0.\)

Приклад\(\PageIndex{6}\): Velocity of a Moving Baseball

Бейсбол кидається вгору з висоти\(3\) метрів над поверхнею Землі з початковою швидкістю\(10\) м/с, і єдиною силою, що діє на нього, є гравітація. Куля має масу\(0.15\) кг на поверхні Землі.

Знайти швидкість\(v(t)\) базової кулі в часі\(t\).
Яка його швидкість через\(2\) секунди?

Рішення

а З попереднього обговорення диференціальне рівняння, яке застосовується в цій ситуації, є

\(v′(t)=−g,\)

де\(g=9.8\, \text{m/s}^2\). Початкова\(v(0)=v_0\) умова - де\(v_0=10\) м/с Тому початкова задача -\(v′(t)=−9.8\,\text{m/s}^2,\,v(0)=10\) м/с.

Першим кроком у розв'язанні цієї початкової задачі є взяття антипохідної обох сторін диференціального рівняння. Це дає

\[\int v′(t)\,dt=∫−9.8\,dt \nonumber \]

\(v(t)=−9.8t+C.\)

Наступний крок - вирішити для\(C\). Для цього підставляємо\(t=0\) і\(v(0)=10\):

\[ \begin{align*} v(t) &=−9.8t+C \\[4pt] v(0) &=−9.8(0)+C \\[4pt] 10 &=C. \end{align*}\]

Тому\(C=10\) і функція швидкості задається\(v(t)=−9.8t+10.\)

b. щоб знайти швидкість через\(2\) секунди, підставити\(t=2\) в\(v(t)\).

\[ \begin{align*} v(t)&=−9.8t+10 \\[4pt] v(2)&=−9.8(2)+10 \\[4pt] v(2) &=−9.6\end{align*}\]

Одиницями швидкості є метри в секунду. Так як відповідь негативна, об'єкт падає зі швидкістю\(9.6\) м/с.

Вправа\(\PageIndex{6}\)

Припустимо, скеля падає з відпочинку з висоти\(100\) метрів і єдиною силою, що діє на неї, є гравітація. Знайдіть рівняння швидкості\(v(t)\) як функцію часу, виміряну в метрах в секунду.

Підказка: Яка початкова швидкість породи? Використовуйте це з диференціальним рівнянням у прикладі,\(\PageIndex{6}\) щоб сформувати початкову задачу, а потім вирішити для\(v(t)\).

Відповідь: \(v(t)=−9.8t\)

Природним питанням, яке слід задати після вирішення цього типу проблеми, є те, наскільки високо об'єкт буде знаходитися над поверхнею Землі в даний момент часу. Нехай\(s(t)\) позначимо висоту над земною поверхнею об'єкта, виміряну в метрах. Оскільки швидкість є похідною від положення (в даному випадку висоти), це припущення дає рівняння\(s′(t)=v(t)\). Необхідно початкове значення, в цьому випадку початкова висота об'єкта працює добре. Нехай початкова висота задається рівнянням\(s(0)=s_0\). Разом ці припущення дають початково-вартісну задачу

\[ s′(t)=v(t),s(0)=s_0. \nonumber \]

Якщо функція швидкості відома, то її можна вирішити і для функції положення.

Приклад\(\PageIndex{7}\): Height of a Moving Baseball

Бейсбол кидається вгору з висоти\(3\) метрів над поверхнею Землі з початковою швидкістю\(10m/s\), і єдиною силою, що діє на нього, є гравітація. Куля має масу\(0.15\) кілограм на поверхні Землі.

Знайдіть положення\(s(t)\) бейсболу на час\(t\).
Яка його висота через\(2\) секунди?

Рішення

Ми вже знаємо, що функція швидкості для цієї задачі є\(v(t)=−9.8t+10\). Початкова висота бейсболу -\(3\) метри, так\(s_0=3\). Тому проблема початкового значення для цього прикладу

Для вирішення початкової задачі спочатку знайдемо антипохідні:

\[∫s′(t)\,dt=∫(−9.8t+10)\,dt \nonumber \]

\(s(t)=−4.9t^2+10t+C.\)

Далі підставляємо\(t=0\) і вирішуємо для\(C\):

\(s(t)=−4.9t^2+10t+C\)

\(s(0)=−4.9(0)^2+10(0)+C\)

\(3=C\).

Тому функція положення є\(s(t)=−4.9t^2+10t+3.\)

б Висота бейсболу після\(2\) сек задається\(s(2):\)

\(s(2)=−4.9(2)^2+10(2)+3=−4.9(4)+23=3.4.\)

Тому бейсбол знаходиться в\(3.4\) метрах над поверхнею Землі через\(2\) секунди. Варто відзначити, що маса м'яча скасована повністю в процесі вирішення завдання.

Ключові поняття

Диференціальне рівняння - це рівняння, що включає функцію\(y=f(x)\) та одну або кілька її похідних. Розв'язок - це функція\(y=f(x)\), яка задовольняє диференціальному рівнянню, коли\(f\) і його похідні підставляються в рівняння.
Порядок диференціального рівняння - це найвищий порядок будь-якої похідної невідомої функції, яка фігурує в рівнянні.
Диференціальне рівняння, пов'язане з початковим значенням, називається початковою задачею. Для розв'язання початково-значної задачі спочатку знайдіть загальний розв'язок диференціального рівняння, потім визначте значення константи. Проблеми початкового значення мають багато застосувань у науці та техніці.

Глосарій

диференційне рівняння: рівняння, що включає функцію\(y=y(x)\) та одну або кілька її похідних

загальне рішення (або сімейство рішень): усю множину розв'язків заданого диференціального рівняння

початкове значення (и): значення або набір значень, що рішення диференціального рівняння задовольняє для фіксованого значення незалежної змінної

початкова швидкість: швидкість в часі\(t=0\)

проблема початкового значення: диференціальне рівняння разом з початковим значенням або значеннями

порядок диференціального рівняння: найвищий порядок будь-якої похідної невідомої функції, що з'являється у рівнянні

конкретне рішення: член сімейства розв'язків диференціального рівняння, що задовольняє певній початковій умові

розв'язок диференціального рівняння: функція,\(y=f(x)\) яка задовольняє заданому диференціальному рівнянню