6.8: Експоненціальне зростання та занепад
- Page ID
- 61670
- Використовуйте модель експоненціального зростання в додатках, включаючи зростання населення та складні відсотки.
- Поясніть поняття подвоєння часу.
- Використовуйте модель експоненціального розпаду в додатках, включаючи радіоактивний розпад та закон охолодження Ньютона.
- Поясніть поняття Half-Life.
Одне з найбільш поширених застосувань експоненціальних функцій включає моделі зростання та розпаду. Експоненціальний ріст і розпад проявляються у безлічі природних застосувань. Від зростання населення і постійно посилюється інтерес до радіоактивного розпаду і закону Ньютона охолодження, експоненціальні функції є повсюдно в природі. У цьому розділі ми розглядаємо експоненціальне зростання та занепад у контексті деяких із цих застосувань.
Модель експоненціального зростання
Багато систем демонструють експоненціальне зростання. Ці системи слідують за моделлю форми,\(y=y_0e^{kt},\) де\(y_0\) представляє початковий стан системи і\(k\) є позитивною константою, яка називається постійною зростання. Зверніть увагу, що в експоненціальній моделі зростання ми маємо
\[ y′=ky_0e^{kt}=ky. \label{eq1} \]
Тобто швидкість зростання пропорційна поточному значенню функції. Це ключова особливість експоненціального зростання. Рівняння\ ref {eq1} включає похідні і називається диференціальним рівнянням.
Системи, що демонструють експоненціальне зростання за математичною моделлю
\[y=y_0e^{kt} \nonumber \]
де\(y_0\) являє собою початковий стан системи і\(k>0\) являє собою константу, звану константою зростання.
Зростання населення є поширеним прикладом експоненціального зростання. Розглянемо, наприклад, популяцію бактерій. Здається правдоподібним, що темпи приросту населення були б пропорційні чисельності населення. Адже чим більше бактерій доведеться розмножуватися, тим швидше зростає популяція. Рисунок\(\PageIndex{1}\) і таблиця\(\PageIndex{1}\) представляють зростання популяції бактерій з початковою популяцією 200 бактерій і константою росту 0,02. Зверніть увагу, що лише через 2 години (120 хвилин) популяція в 10 разів перевищує початковий розмір!
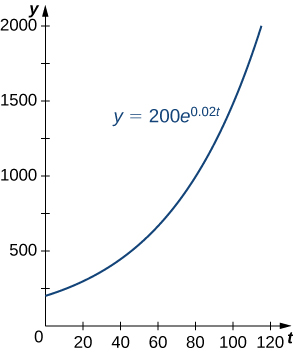
| Час (хв) | Чисельність населення (кількість бактерій) |
|---|---|
| 10 | 244 |
| 20 | 298 |
| 30 | 364 |
| 40 | 445 |
| 50 | 544 |
| 60 | 664 |
| 70 | 811 |
| 80 | 991 |
| 90 | 1210 |
| 100 | 1478 |
| 110 | 1805 |
| 120 | 2205 |
Зауважте, що ми використовуємо безперервну функцію для моделювання того, що за своєю суттю є дискретною поведінкою. У будь-який момент часу реальна популяція містить цілу кількість бактерій, хоча модель приймає неціле значення. Використовуючи моделі експоненціального зростання, ми завжди повинні бути обережними, щоб інтерпретувати значення функцій в контексті явища, яке ми моделюємо.
Розглянемо популяцію бактерій, описаних раніше. Ця популяція зростає відповідно до функції\(f(t)=200e^{0.02t},\), де t вимірюється в хвилинах. Скільки бактерій присутній в популяції після\(5\) години (\(300\)хвилин)? Коли популяція досягає\(100,000\) бактерій?
Рішення
У нас є\(f(t)=200e^{0.02t}.\) Тоді
\[ f(300)=200e^{0.02(300)}≈80,686. \nonumber \]
Є\(80,686\) бактерії в популяції в\(5\) неробочий час.
Щоб знайти, коли популяція досягає\(100,000\) бактерій, вирішуємо рівняння
\[ \begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber \]
Популяція досягає\(100,000\) бактерій через\(310.73\) кілька хвилин.
Розглянемо популяцію бактерій, яка росте відповідно до функції\(f(t)=500e^{0.05t}\), де\(t\) вимірюється в хвилинах. Скільки бактерій присутній в популяції через 4 години? Коли популяція досягає\(100\) мільйона бактерій?
- Відповідь
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Є\(81,377,396\) бактерії в популяції в\(4\) неробочий час. Населення досягає\(100\) мільйона бактерій через\(244.12\) кілька хвилин.
Давайте тепер звернемо увагу на фінансове застосування: складні відсотки. Інтерес, який не посилюється, називається простим інтересом. Прості відсотки виплачуються один раз, в кінці зазначеного періоду часу (зазвичай\(1\) року). Отже, якщо ми\($1000\) вкладаємо на ощадний рахунок заробіток\(2%\) простих відсотків за рік, то в кінці року у нас є
\[ 1000(1+0.02)=$1020. \nonumber \]
Складні відсотки виплачуються кілька разів на рік, залежно від періоду складання. Тому, якщо банк\(6\) щомісяця нараховує відсотки, він зараховує половину річних відсотків на рахунок через\(6\) місяці. Протягом другого півріччя на рахунку нараховуються відсотки не тільки на початкові\($1000\), але і на відсотки, зароблені протягом першого півріччя. Математично кажучи, наприкінці року ми маємо
\[ 1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber \]
Аналогічно, якщо інтерес посилюється\(4\) щомісяця, ми маємо
\[ 1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber \]
і якщо відсотки посилюються щодня (\(365\)раз на рік), у нас є\($1020.20\). Якщо ми продовжимо цю концепцію, щоб інтерес постійно посилювався, через\(t\) роки ми маємо
\[ 1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber \]
Тепер давайте маніпулювати цим виразом так що у нас є експоненціальна функція зростання. Нагадаємо, що число\(e\) може бути виражено у вигляді ліміту:
\[ e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber \]
Виходячи з цього, ми хочемо, щоб вираз всередині дужок мав форму\((1+1/m)\). Нехай\(n=0.02m\). Зауважте, що\(n→∞, m→∞\) також. Тоді ми отримуємо
\[ 1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber \]
Ліміт всередині дужок визнаємо як число\(e\). Отже, залишок на нашому банківському рахунку через\(t\) роки дається\(1000 e^{0.02t}\). Узагальнюючи це поняття, ми бачимо, що якщо банківський рахунок з початковим залишком\($P\) заробляє відсотки за ставкою\(r%\), що ускладнюється безперервно, то залишок рахунку через\(t\) роки становить
\[ \text{Balance}\;=Pe^{rt}. \nonumber \]
25-річному студенту пропонується можливість вкласти трохи грошей на пенсійний рахунок, який сплачує\(5%\) щорічні відсотки, що складаються безперервно. Скільки студенту потрібно інвестувати сьогодні, щоб мати\($1\) мільйон, коли вона виходить на пенсію у віці\(65\)? Що робити, якби вона могла заробляти\(6%\) щорічні відсотки, що постійно посилюються замість цього?
Рішення
У нас є
\[ 1,000,000=Pe^{0.05(40)} \nonumber \]
\[ P=135,335.28. \nonumber \]
Вона повинна інвестувати\($135,335.28\) під\(5%\) відсотки.
Якщо замість цього вона здатна заробляти,\(6%,\) то рівняння стає
\[ 1,000,000=Pe^{0.06(40)} \nonumber \]
\[ P=90,717.95. \nonumber \]
У цьому випадку їй потрібно інвестувати лише\($90,717.95.\) Це приблизно дві третини суми, яку їй потрібно інвестувати\(5%\). Той факт, що відсотки постійно посилюються, значно збільшує ефект від\(1%\) підвищення процентної ставки.
Припустимо, замість того\(25\sqrt{b^2−4ac}\), щоб інвестувати у віці, студент чекає до віку\(35\). Скільки їй довелося б інвестувати\(5%\)? В\(6%\)?
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Під\(5%\) відсотки вона повинна інвестувати\($223,130.16\). Під\(6%\) відсотки вона повинна інвестувати\($165,298.89.\)
Якщо кількість зростає експоненціально, час, необхідний для подвоєння кількості, залишається постійним. Іншими словами, потрібно стільки ж часу, щоб популяція бактерій виросла від\(100\) до\(200\) бактерій, як і рости від\(10,000\) до\(20,000\) бактерій. Цей час називається часом подвоєння. Щоб розрахувати час подвоєння, ми хочемо знати, коли кількість досягне удвічі більше початкового розміру. Отже, у нас є
\[ \begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber \]
Якщо кількість зростає експоненціально, час подвоєння - це кількість часу, на який потрібно подвоїти кількість. Це дається
\[\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber \]
Припустимо, що популяція риби зростає в геометричній прогресії. Ставок спочатку запасається\(500\) рибою. Через\(6\) місяці в водоймі з'являються\(1000\) риби. Господар дозволить своїм друзям і сусідам ловити рибу на своєму водоймі після того, як досягне популяція риб\(10,000\). Коли друзям господаря дозволять ловити рибу?
Рішення
Ми знаємо, що популяція риб\(6\) місяці займає подвоєння в розмірі. Отже, якщо\(t\) представляє час у місяцях, за формулою подвоєння часу, ми маємо\(6=(\ln 2)/k\). Потім,\(k=(\ln 2)/6\). Таким чином, населення дається по\(y=500e^{((\ln 2)/6)t}\). Щоб з'ясувати, коли популяція досягає\(10,000\) риби, треба вирішити наступне рівняння:
\[ \begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber \]
Друзям господаря доводиться чекати\(25.93\) місяці (трохи більше\(2\) років), щоб рибалити в ставку.
Припустимо, для того, щоб популяція риби в Прикладі\(\PageIndex{3}\) досягла\(1000\) риби, потрібні\(9\) місяці. За цих обставин, як довго доводиться чекати друзям власника?
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
\(38.90\)місяців
Модель експоненціального розпаду
Експоненціальні функції також можуть бути використані для моделювання популяцій, які скорочуються (наприклад, від хвороб), або хімічних сполук, які руйнуються з часом. Ми говоримо, що такі системи демонструють експоненціальний розпад, а не експоненціальне зростання. Модель майже така ж, за винятком того, що в показнику присутній негативний знак. Таким чином, для деякої позитивної\(k\) константи ми маємо
\[ y=y_0e^{−kt}. \nonumber \]
Як і при експоненціальному зростанні, існує диференціальне рівняння, пов'язане з експоненціальним розпадом. У нас є
\[ y′=−ky_0e^{−kt}=−ky. \nonumber \]
Системи, що демонструють експоненціальний розпад, поводяться відповідно до моделі
\[y=y_0e^{−kt}, \nonumber \]
де\(y_0\) представляє початковий стан системи і\(k>0\) є постійною, званої постійною розпаду.
На малюнку\(\PageIndex{2}\) показаний графік репрезентативної експоненціальної функції розпаду.
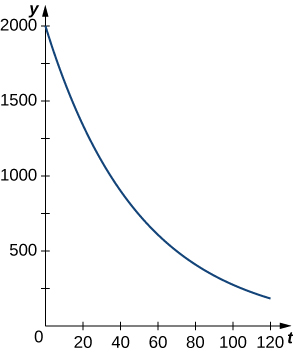
Давайте розглянемо фізичне застосування експоненціального розпаду. Закон охолодження Ньютона говорить про те, що об'єкт охолоджується зі швидкістю, пропорційною різниці між температурою об'єкта і температурою оточення. Іншими словами, якщо\(T\) представляє температуру об'єкта і\(T_a\) представляє температуру навколишнього середовища в приміщенні, то
\[T′=−k(T−T_a). \nonumber \]
Зверніть увагу, що це не зовсім правильна модель для експоненціального розпаду. Ми хочемо, щоб похідна була пропорційною функції, і цей вираз має додатковий\(T_a\) термін. На щастя, ми можемо внести зміни змінних, які вирішують цю проблему. Нехай\(y(t)=T(t)−T_a\). Потім\(y′(t)=T′(t)−0=T′(t)\), і наше рівняння стає
\[ y′=−ky. \nonumber \]
З нашої попередньої роботи ми знаємо, що цей зв'язок між\(y\) і його похідною призводить до експоненціального розпаду. Таким чином,
\[ y=y_0e^{−kt}, \nonumber \]
і ми бачимо, що
\[ T−T_a=(T_0−T_a)e^{−kt} \nonumber \]
\[ T=(T_0−T_a)e^{−kt}+T_a \nonumber \]
де\(T_0\) представляє початкову температуру. Давайте застосуємо цю формулу в наступному прикладі.
На думку досвідчених бариста, оптимальна температура для подачі кави - між\(155°F\) і\(175°F\). Припустимо, каву наливають при температурі\(200°F\), а через\(2\) хвилини в\(70°F\) приміщенні він охолоне до\(180°F\). Коли кава вперше досить прохолодна, щоб подати? Коли кава занадто холодна, щоб подавати? Круглі відповіді до найближчих півхвилини.
Рішення
У нас є
\[ \begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}\]
Тоді модель
\[T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber \]
Кава досягає,\(175°F\) коли
\[ \begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}\]
Каву можна подавати приблизно через\(2.5\) кілька хвилин після того, як він буде залитий. Кава досягає\(155°F\)
\[ \begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}\]
Кава занадто холодна, щоб його подавали приблизно через\(5\) кілька хвилин після того, як його заливають.
Припустимо, в кімнаті тепліше,\((75°F)\) і через\(2\) кілька хвилин кава охолола лише до\(185°F.\) Коли кава спочатку досить прохолодна, щоб подати? Коли кава буде занадто холодною, щоб подавати? Круглі відповіді до найближчих півхвилини.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Кава спочатку досить охолодити, щоб подавати приблизно\(3.5\) хвилин після того, як його заливають. Кава занадто холодна, щоб подавати приблизно\(7\) хвилин після того, як його заливають.
Подібно до того, як системи, що демонструють експоненціальне зростання, мають постійний час подвоєння, системи, що демонструють експоненціальний розпад, мають постійний період напіврозпаду. Щоб розрахувати період напіврозпаду, ми хочемо знати, коли кількість досягає половини свого початкового розміру. Тому у нас є
\(\dfrac{y_0}{2}=y_0e^{−kt}\)
\(\dfrac{1}{2}=e^{−kt}\)
\(−\ln 2=−kt\)
\(t=\dfrac{\ln 2}{k}\).
Примітка: Це той самий вираз, який ми придумали для подвоєння часу.
Якщо кількість розпадається експоненціально, період напіврозпаду є кількість часу, який він приймає кількість, щоб бути зменшені наполовину. Це дається
\[\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber \]
Одним з найпоширеніших застосувань моделі експоненціального розпаду є датування вуглецю. Вуглець-14 розпадається (виділяє радіоактивну частинку) з регулярною і послідовною експоненціальною швидкістю. Тому, якщо ми знаємо, скільки вуглецю-14 спочатку було присутнє в об'єкті і скільки залишилося вуглецю-14, можна визначити вік об'єкта. Період напіврозпаду вуглецю-14 становить приблизно 5730 років, тобто після цього багато років половина матеріалу перетворилася з вихідного вуглецю-14 в новий нерадіоактивний азот-14. Якщо у нас сьогодні 100 г вуглецю-14, скільки залишилося через 50 років? Якщо артефакт, який спочатку містив 100 г вуглецю-14, тепер містить 10 г вуглецю-14, скільки йому років? Округлити відповідь до найближчої сотні років.
Рішення
У нас є
\[ 5730=\dfrac{\ln 2}{k} \nonumber \]
\[ k=\dfrac{\ln 2}{5730}.\nonumber \]
Отже, модель говорить
\[ y=100e^{−(\ln 2/5730)t}.\nonumber \]
У\(50\) роки ми маємо
\[y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber \]
Тому в\(50\) роки зберігається\(99.40\) г вуглецю-14.
Щоб визначити вік артефакту, ми повинні вирішити
\[ \begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}\]
Артефакту близько\(19,000\) років.
Якщо у нас 100 г вуглецю-14 , скільки залишилося після 500 років? Якщо артефакт, який спочатку містив 100 г вуглецю-14 тепер містить 20 г вуглецю-14, скільки йому років? Округлити відповідь до найближчої сотні років.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Всього 94,13 г вуглецю-14 залишається після 500 років. Артефакту приблизно 13 300 років.
Ключові концепції
- Експоненціальне зростання і експоненціальний розпад є двома найпоширенішими додатками експоненціальних функцій.
- Системи, які демонструють експоненціальне зростання, слідують моделі форми\(y=y_0e^{kt}\).
- При експоненціальному зростанні швидкість зростання пропорційна присутній кількості. Іншими словами,\(y′=ky\).
- Системи, що демонструють експоненціальне зростання, мають постійне подвоєння часу, яке задається\((\ln 2)/k\).
- Системи, що демонструють експоненціальний розпад, слідують моделі форми\(y=y_0e^{−kt}.\)
- Системи, що демонструють експоненціальний розпад, мають постійний період напіврозпаду, який задається\((\ln 2)/k.\)
Глосарій
- подвоєння часу
- якщо кількість зростає в геометричній прогресії, подвоєння час - це кількість часу, яку потрібно подвоїти, і задається\((\ln 2)/k\)
- експоненціальний розпад
- системи, які демонструють експоненціальний розпад, слідують моделі форми\(y=y_0e^{−kt}\)
- експоненціальне зростання
- системи, які демонструють експоненціальне зростання, слідують моделі форми\(y=y_0e^{kt}\)
- період напіврозпаду
- Якщо кількість розпадається експоненціально, період напіврозпаду є кількість часу, який він приймає кількість, щоб бути зменшені наполовину. Це дається\((\ln 2)/k\)
