4.11: Глава 4 Огляд вправи

Last updated
Save as PDF

Page ID: 62146

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Правда чи брехня? Обгрунтуйте свою відповідь доказом або зустрічнимприкладом. Припустимо, що$f(x)$ це безперервний і диференційований, якщо не вказано інше

1) Якщо$f(−1)=−6$ і$f(1)=2$, то існує хоча б одна точка$x∈[−1,1]$ така, що$f′(x)=4.$

Відповідь: Правда, за середнім значенням теореми

2) Якщо$f′(c)=0,$ є максимум або мінімум при$x=c.$

3) Є функція така, що$f(x)<0,f′(x)>0,$ і$f''(x)<0.$ (Графічний «доказ» прийнятний для цієї відповіді.)

Відповідь: Правда

4) Існує така функція, що є як точка перегину, так і критична точка для деякого значення$x=a.$

5) З огляду на графік$f′$, визначають, де$f$ відбувається збільшення або зменшення.

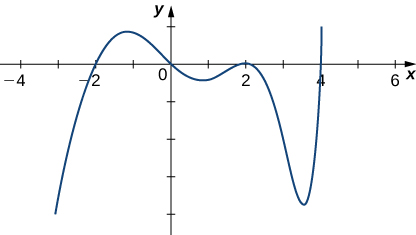
$Функція збільшується, щоб перетнути вісь x на −2, досягає максимуму, а потім зменшується через початок, досягає мінімуму, а потім збільшується до максимуму на 2, зменшується до мінімуму, а потім збільшується, щоб пройти через вісь x на 4 і продовжує збільшуватися.$

Відповідь: Збільшення:$(−2,0)∪(4,∞)$, зменшення:$(−∞,−2)∪(0,4)$

6) Графік$f$ наведено нижче. Малюйте$f′$.

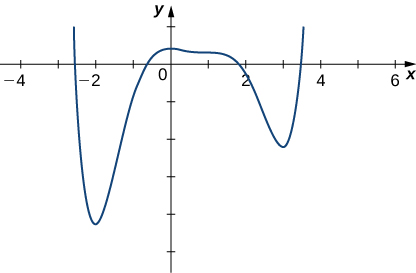
$Функція швидко зменшується і досягає локального мінімуму при −2, потім вона збільшується до локального максимуму в 0, в цей момент вона спочатку повільно зменшується, потім припиняє зменшуватися поблизу 1, потім продовжує зменшуватися до мінімуму на 3, а потім швидко зростає.$

7) Знайти лінійне наближення$L(x)$ до$y=x^2+\tan(πx)$ ближнього$x=\frac{1}{4}.$

Відповідь: $L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)\left(x−\frac{1}{4}\right)$

8) Знайти диференціал$y=x^2−5x−6$ і оцінити для$x=2$ з$dx=0.1.$

Знайти критичні точки і локальну і абсолютну крайність наступних функцій на заданому інтервалі.

9)$f(x)=x+\sin^2(x)$ над$[0,π]$

Відповідь: Критична точка:$x=\frac{3π}{4},$
Абсолютний мінімум:$0$ коли$x=0,$
Абсолютний максимум:$π$ коли$x=π$

Рішення:

10)$f(x)=3x^4−4x^3−12x^2+6$ понад$[−3,3]$

Визначте, над якими інтервалами наступні функції збільшуються, зменшуються, увігнуті вгору і увігнуті вниз.

11)$x(t)=3t^4−8t^3−18t^2$

Відповідь: Збільшення:$(−1,0)∪(3,∞),$
зменшення:$(−∞,−1)∪(0,3),$
увігнуті вгору:$\left(−∞,\frac{1}{3}\left(2−\sqrt{13}\right)\right)∪\left(\frac{1}{3}\left(2+\sqrt{13}\right),∞\right)$,
увігнуті вниз:$\left(\frac{1}{3}\left(2−\sqrt{13}\right),\frac{1}{3}\left(2+\sqrt{13}\right)\right)$

12)$y=x+\sin(πx)$

13)$g(x)=x−\sqrt{x}$

Відповідь: Збільшення:$\left(\frac{1}{4},∞\right),$
зменшення:$\left(0,\frac{1}{4}\right)$,
увігнуті вгору:$(0,∞),$
увігнуті вниз: ніде

14)$f(θ)=\sin(3θ)$

Оцініть наступні межі.

15)$\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Відповідь: $3$

16)$\displaystyle \lim_{x→∞}\cos\left(\frac{1}{x}\right)$

17)$\displaystyle \lim_{x→1}\frac{x−1}{\sin(πx)}$

Відповідь: $−\frac{1}{π}$

18)$\displaystyle \lim_{x→∞}(3x)^{1/x}$

Використовуйте метод Ньютона, щоб знайти перші дві ітерації, задані початковою точкою.

19)$y=x^3+1,\quad x_0=0.5$

Відповідь: $x_1=−1,\; x_2=−1$

20)$\dfrac{1}{x+1}=\dfrac{1}{2}, \quad x_0=0$

Знайдіть$F(x)$ антипохідні наступних функцій.

21)$g(x)=\sqrt{x}−\dfrac{1}{x^2}$

Відповідь: $F(x)=\dfrac{2x^{3/2}}{3}+\dfrac{1}{x}+C$

22)$f(x)=2x+6\cos x,\quad F(π)=π^2+2$

Графік наступних функцій вручну. Не забудьте позначити точки перегину, критичні точки, нулі та асимптоти.

23)$y=\dfrac{1}{x(x+1)^2}$

Відповідь

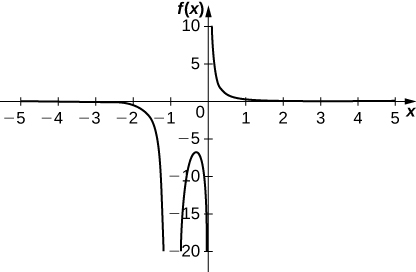
$Цей графік має вертикальні асимптоти при x = 0 і x = −1. Перша частина функції відбувається в третьому квадранті з горизонтальною асимптотою при y = 0. Функція швидко зменшується від ближньої (−5, 0) до близької вертикальної асимптоти (−1, ∞). З іншого боку асимптоти функція має приблизно U-подібну форму і спрямована вниз у третьому квадранті між x = −1 та x = 0 з максимальним числом поблизу (−0,4, −6). З іншого боку асимпотота x = 0, функція зменшується від своєї вертикальної асимптоти поблизу (0, ∞) і наближається до горизонтальної асимптоти y = 0.$

Точки перегину: немає;
Критичні точки:$x=−\frac{1}{3}$;
Нулі: немає;
Вертикальні асимптоти:$x=−1, \; x=0$;
Горизонтальна асимптота:$y=0$

24)$y=x−\sqrt{4−x^2}$

25) Автомобіль ущільнюється в прямокутне тверде тіло. Обсяг зменшується зі швидкістю$2\, \text{m}^3/\text{sec}$. Довжина і ширина ущільнювача квадратні, але висота не така ж довжина, як довжина і ширина. Якщо довжина і ширина стін рухаються назустріч один одному зі швидкістю$0.25$ м/сек, знайдіть швидкість, з якою змінюється висота, коли довжина і ширина -$2$ м, а висота -$1.5$ м.

Відповідь: Висота зменшується зі швидкістю$0.125$ м/сек

26) Ракета запускається в космос; її кінетична енергія$K$ задається тим$K(t)=\frac{1}{2}m(t)v(t)^2$, де кінетична енергія в джоулі,$m$ це маса ракети в кілограмах, а$v$ швидкість ракети в метрах/секунду. Припустимо, що швидкість збільшується зі швидкістю,$15 \,\text{m/sec}^2$ а маса зменшується зі швидкістю$10$ кг/сек, оскільки паливо спалюється. З якою швидкістю змінюється кінетична енергія ракети при масі$2000$ кг і швидкості$5000$ м/сек? Дайте свою відповідь в мега-джоулі (MJ), що еквівалентно J$10^6$.

27) Знаменита проблема Регіомонтана щодо максимізації кута була запропонована протягом$15^\text{th}$ століття. Картина висить на стіні з нижньою частиною картини на відстані$a$ футів вище рівня очей, а верхні$b$ ноги вище рівня очей. Яку відстань$x$ (у футах) від стіни повинен стояти глядач, щоб максимізувати кут, поглиблений картиною$θ$?

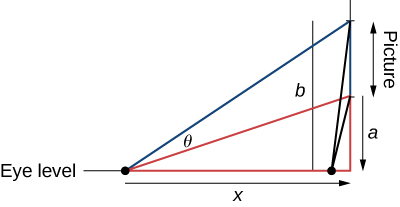
$Відзначається точка рівня очей, і від цієї точки робиться прямокутний трикутник з довжиною сусідньої сторони x і довжиною протилежної сторони a, яка є довжиною від нижньої частини малюнка до рівня ока. Другий прямокутний трикутник робиться з точки, позначеної рівнем очей, при цьому сусідня сторона дорівнює x, а інша сторона - довжина b, яка є висотою малюнка. Кут між двома гіпотенусами позначається θ.$

Відповідь: $x=\sqrt{ab}$ноги

28) Авіакомпанія продає квитки з Токіо в Детройт для$$1200.$ Є доступні$500$ місця та типові польотні книги$350$ місць. За кожне$$10$ зниження ціни авіакомпанія спостерігає додатково п'ять проданих місць. Яким повинен бути тариф, щоб отримати максимальний прибуток? Скільки пасажирів було б на борту?