4.3: Максима і Мініма

Last updated
Save as PDF

Page ID: 62154

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визначте абсолютну крайність.
Визначте локальні крайності.
Поясніть, як знайти критичні точки функції за замкнутий інтервал.
Опишіть, як використовувати критичні точки для визначення абсолютної крайності за замкнутий інтервал.

З огляду на ту чи іншу функцію, ми часто зацікавлені у визначенні найбільших і найменших значень функції. Ця інформація важлива при створенні точних графіків. Пошук максимального та мінімального значень функції також має практичне значення, оскільки ми можемо використовувати цей метод для вирішення проблем оптимізації, таких як максимізація прибутку, мінімізація кількості матеріалу, що використовується при виготовленні алюмінієвої банки, або знаходження максимальної висоти, яку може досягти ракета. У цьому розділі ми розглянемо, як за допомогою похідних знайти найбільші та найменші значення для функції.

Абсолютна Екстрема

Розглянемо функцію\(f(x)=x^2+1\) над інтервалом\((−∞,∞)\). Як\(x→±∞, f(x)→∞\). Тому функція не має найбільшого значення. Однак, оскільки\(x^2+1≥1\) для всіх дійсних чисел\(x\) і\(x^2+1=1\) коли\(x=0\) функція має найменше значення\(1\), коли\(x=0\). Ми говоримо, що\(1\) є абсолютним мінімумом\(f(x)=x^2+1\) і це відбувається при\(x=0\). Ми говоримо, що\(f(x)=x^2+1\) не має абсолютного максимуму (рис.\(\PageIndex{1}\)).

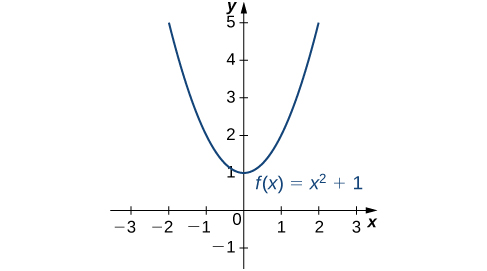
Функція f (x) = x ^ 2 + 1 графічна, а її мінімум 1, як видно, знаходиться при x = 0. — Малюнок\(\PageIndex{1}\): Дана функція має абсолютний мінімум\(1\) at\(x=0\). Функція не має абсолютного максимуму.

Визначення: Абсолютна Екстрема

\(f\)Дозволяти бути функція, визначена протягом інтервалу\(I\) і нехай\(c∈I\). Ми говоримо, що\(f\) має абсолютний максимум\(I\) на,\(c\) якщо\(f(c)≥f(x)\) для всіх\(x∈I\). Ми говоримо, що\(f\) має абсолютний\(I\) мінімум на,\(c\) якщо\(f(c)≤f(x)\) для всіх\(x∈I\). Якщо\(f\) має абсолютний максимум на\(I\) at\(c\) або абсолютний мінімум на\(I\) at\(c\), ми говоримо, що\(f\) має абсолютний екстремум на\(I\) at\(c\).

Перш ніж приступити, відзначимо два важливих питання, що стосуються даного визначення. По-перше, термін абсолютний тут не відноситься до абсолютного значення. Абсолютний екстремум може бути позитивним, негативним або нульовим. По-друге, якщо функція\(f\) має абсолютний екстремум протягом інтервалу\(I\) в\(c\), абсолютний екстремум дорівнює\(f(c)\). Реальне число\(c\) - це точка в області, в якій відбувається абсолютний екстремум. Наприклад, розглянемо функцію\(f(x)=1/(x^2+1)\) над інтервалом\((−∞,∞)\). Так як

\[f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber \]

для всіх дійсних чисел\(x\), ми говоримо,\(f\) має абсолютний максимум над\((−∞,∞)\) в\(x=0\). Абсолютний максимум - це\(f(0)=1\). Відбувається вона при\(x=0\), як показано на малюнку\(\PageIndex{2}\) (б).

Функція може мати як абсолютний максимум, так і абсолютний мінімум, лише один екстремум, або ні ні. \(\PageIndex{2}\)На малюнку показано кілька функцій та деякі з різних можливостей щодо абсолютних екстремумів. Однак наступна теорема, яка називається теоремою крайніх значень, гарантує, що безперервна функція\(f\) через замкнутий обмежений інтервал\([a,b]\) має як абсолютний максимум, так і абсолютний мінімум.

Ця цифра складається з шести частин a, b, c, d, e і f На малюнку a показана лінія f (x) = x^3, і зазначається, що вона не має абсолютного мінімуму і абсолютного максимуму. На малюнку b показано лінію f (x) = 1/ (x^2 + 1), яка майже 0 для більшої частини своєї довжини і піднімається до удару при (0, 1); вона не має абсолютного мінімуму, але має абсолютний максимум 1 при x = 0. На малюнку c показано лінію f (x) = cos x, яка має абсолютні мінімуми −1 при ± π, ± 3π,... і абсолютні максимуми 1 при 0, ± 2π, ± 4π,... На малюнку d показано кускову функцію f (x) = 2 — x^2 для 0 ≤ x < 2 та x — 3 для 2 ≤ x ≤ 4, абсолютний максимум 2 при x = 0 і абсолютний мінімум відсутній. На малюнку e функція f (x) = (x — 2) 2 показана на [1, 4], яка має абсолютний максимум 4 при x = 4 і абсолютний мінімум 0 при x = 2. На малюнку f функція f (x) = x/ (2 − x) показана на [0, 2), абсолютний мінімум 0 при x = 0 і не абсолютний максимум. — Рисунок\(\PageIndex{2}\): Графіки (a), (b) та (c) показують кілька можливостей абсолютної крайності для функцій з областю\((−∞,∞).\) графів (d), (e) та (f) показують кілька можливостей абсолютної крайності для функцій з областю, яка є обмеженим інтервалом.

Теорема\(\PageIndex{1}\): Extreme Value Theorem

Якщо\(f\) є безперервною функцією над замкнутим\([a,b]\), обмеженим інтервалом, то є точка в\([a,b]\) якій\(f\) має абсолютний максимум над\([a,b]\) і є точка в\([a,b]\) якій\(f\) має абсолютний мінімум понад\([a,b]\).

Доказ теореми про крайні значення виходить за рамки цього тексту. Як правило, це доведено в курсі на реальному аналізі. Є кілька ключових моментів, які слід зазначити щодо твердження цієї теореми. Щоб застосувати теорему про крайні значення, функція повинна бути неперервною через замкнутий обмежений інтервал. Якщо інтервал\(I\) відкритий або функція має навіть одну точку розриву, функція може не мати абсолютного максимуму або абсолютного мінімуму понад\(I\). Наприклад, розглянемо функції, показані на малюнку\(\PageIndex{2}\) (d), (e) і (f). Всі три з цих функцій визначаються через обмежені інтервали. Однак функція в графі (e) є єдиною, яка має як абсолютний максимум, так і абсолютний мінімум над своєю областю. Теорема про крайні значення не може бути застосована до функцій у графах (d) та (f), оскільки жодна з цих функцій не є безперервною через замкнутий обмежений інтервал. Хоча функція в графі (d) визначається через замкнутий інтервал\([0,4]\), функція є переривчастою в\(x=2\). Функція має абсолютний максимум понад,\([0,4]\) але не має абсолютного мінімуму. Функція в графі (f) є неперервною протягом напіввідкритого інтервалу\([0,2)\), але не визначена в\(x=2\), а отже, не є безперервною протягом замкнутого обмеженого інтервалу. Функція має абсолютний мінімум понад\([0,2)\), але не має абсолютного максимуму понад\([0,2)\). Ці два графіки ілюструють, чому функція через обмежений інтервал може не мати абсолютного максимуму та/або абсолютного мінімуму.

Перш ніж дивитися на те, як знайти абсолютну крайність, давайте розберемо пов'язане поняття локальної екстреми. Ця ідея корисна при визначенні того, де відбуваються абсолютні екстремуми.

Локальні екстреми і критичні точки

Розглянемо функцію,\(f\) зображену на малюнку\(\PageIndex{3}\). Графік можна описати як дві гори з долиною посередині. Абсолютне максимальне значення функції відбувається на більш високому піку, в\(x=2\). Однак\(x=0\) це також цікава точка. Хоча\(f(0)\) це не найбільше значення\(f\), значення більше\(f(0)\), ніж\(f(x)\) для всіх\(x\) близько 0. Ми говоримо, що\(f\) має локальний максимум на\(x=0\). Аналогічно, функція\(f\) не має абсолютного мінімуму, але вона має локальний мінімум в\(x=1\) тому,\(f(1)\) що менше, ніж\(f(x)\) для\(x\) близько 1.

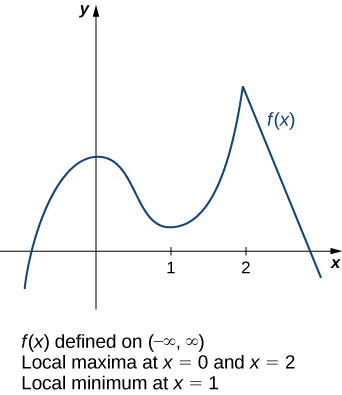
Показано функцію f (x), яка крива вгору від квадранта III, сповільнюється в квадранті II, досягає локального максимуму на осі y, зменшується для досягнення локального мінімуму в квадранті I при x = 1, збільшується до локального максимуму при x = 2, що більше іншого локального максимуму, а потім швидко зменшується через квадрант IV. — Малюнок\(\PageIndex{3}\): Ця функція\(f\) має два локальних максимума і один локальний мінімум. Локальний максимум при\(x=2\) - це також абсолютний максимум.

Визначення: Локальна Екстрема

Функція\(f\) має локальний максимум\(c\) при наявності відкритого інтервалу, що\(I\) містить\(c\)\(I\) такий, який міститься в області\(f\) та\(f(c)≥f(x)\) для всіх\(x∈I\). Функція\(f\) має локальний мінімум,\(c\) якщо існує відкритий інтервал, що\(I\) містить\(c\)\(I\) такий, який міститься в області\(f\) та\(f(c)≤f(x)\) для всіх\(x∈I\). Функція\(f\) має локальний екстремум при\(c\) якщо\(f\) має локальний максимум на\(c\) або\(f\) має локальний мінімум на\(c\).

Зверніть увагу, що якщо\(f\) має абсолютний екстремум в\(c\) і\(f\) визначається протягом інтервалу\(c\), що містить, то також\(f(c)\) вважається локальним екстремумом. Якщо абсолютний екстремум для функції\(f\) відбувається в кінцевій точці, ми не вважаємо, що бути локальним екстремумом, а замість цього посилатися на це як кінцева точка екстремум.

Враховуючи графік функції\(f\), іноді легко побачити, де відбувається локальний максимум або локальний мінімум. Однак це не завжди легко побачити, оскільки цікаві функції на графіку функції можуть бути не помітні, оскільки вони відбуваються в дуже маленькому масштабі. Крім того, у нас може не бути графіка функції. У цих випадках, як ми можемо використовувати формулу для функції, щоб визначити, де відбуваються ці крайності?

Щоб відповісти на це питання, давайте\(\PageIndex{3}\) знову подивимося на малюнок. Локальні крайності виникають при\(x=0, x=1,\) і\(x=2.\) Зверніть увагу, що при\(x=0\) і\(x=1\), похідне\(f'(x)=0\). При\(x=2\), похідної\(f'(x)\) не існує, так як функція\(f\) має там кут. Насправді, якщо в точці\(f\) є локальний екстремум\(x=c\), похідна\(f'(c)\) повинна задовольняти одній з наступних умов:\(f'(c)=0\) або або\(f'(c)\) є невизначеною. Така величина\(c\) відома як критична точка і вона важлива при знаходженні екстремальних значень для функцій.

Визначення: Критичні точки

\(c\)Дозволяти бути внутрішньою точкою в області\(f\). Ми говоримо, що\(c\) є критичною точкою\(f\) якщо\(f'(c)=0\) або\(f'(c)\) не визначено.

Як вже говорилося раніше, якщо\(f\) має локальний екстремум в точці\(x=c\), то\(c\) повинна бути критична точка\(f\). Цей факт відомий як теорема Ферма.

Теорема\(\PageIndex{2}\): Fermat’s Theorem

Якщо\(f\) має локальний екстремум при\(c\) і\(f\) диференційований при\(c\), то\(f'(c)=0.\)

Доказ

Припустимо,\(f\) має локальний екстремум при\(c\) і\(f\) диференційований при\(c\). Нам потрібно це показати\(f'(c)=0\). Для цього ми покажемо, що\(f'(c)≥0\) і\(f'(c)≤0\), а значить\(f'(c)=0\). Так як\(f\) має локальний екстремум при\(c\),\(f\) має локальний максимум або локальний мінімум при\(c\). Припустимо,\(f\) має локальний максимум при\(c\). Справа, в якій\(f\) має локальний мінімум at,\(c\) може бути оброблений аналогічно. Там тоді існує відкритий інтервал я такий, що\(f(c)≥f(x)\) для всіх\(x∈I\). Оскільки\(f\) диференціюється при\(c\), від визначення похідної, ми знаємо, що

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Оскільки ця межа існує, обидва односторонні межі також існують і рівні\(f'(c)\). Тому,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2} \]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Оскільки\(f(c)\) це локальний максимум, ми бачимо, що\(f(x)−f(c)≤0\) для\(x\) ближнього\(c\). Тому для\(x\) ближнього\(c\), але\(x>c\), у нас є\(\frac{f(x)−f(c)}{x−c}≤0\). З рівняння\ ref {FermateQn2} ми робимо висновок, що\(f'(c)≤0\). Так само можна показати, що\(f'(c)≥0.\) Тому,\(f'(c)=0.\)

□

З теореми Ферма ми робимо висновок, що якщо\(f\) має локальний екстремум at\(c\), то або\(f'(c)=0\) або\(f'(c)\) не визначено. Іншими словами, локальна екстремія може виникати тільки в критичних точках.

Зверніть увагу, що ця теорема не стверджує, що функція\(f\) повинна мати локальний екстремум у критичній точці. Швидше, в ньому зазначено, що критичні точки є кандидатами на локальну екстрему. Для прикладу розглянемо функцію\(f(x)=x^3\). У нас є\(f'(x)=3x^2=0\) коли\(x=0\). Тому\(x=0\) є критичною точкою. Однак\(f(x)=x^3\) збільшується більше, і\((−∞,∞)\), таким чином,\(f\) не має локального екстремуму при\(x=0\). На малюнку\(\PageIndex{4}\) ми бачимо кілька різних можливостей для критичних точок. У деяких з цих випадків функції мають локальну крайність в критичних точках, тоді як в інших випадках функції - ні. Зауважте, що ці графіки не показують всіх можливостей поведінки функції в критичній точці.

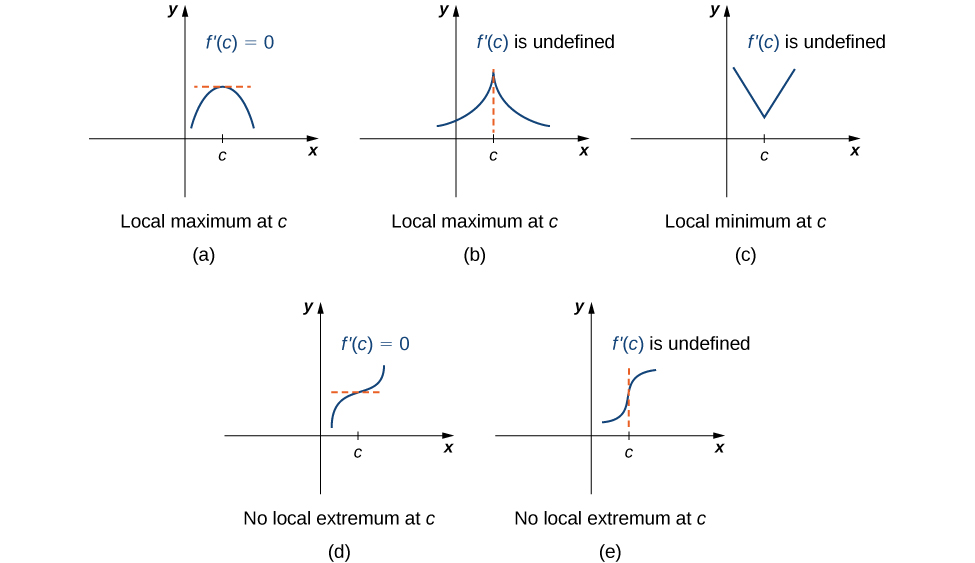
Ця цифра складається з п'яти частин a, b, c, d і e На малюнку a парабола показана зверненою вниз в квадранті I; є горизонтальна дотична лінія на локальному максимумі, позначеному f' (c) = 0. На малюнку b є функція, намальована з асимптотою в c, що означає, що функція збільшується до нескінченності по обидва боки c; зазначається, що f' (c) не визначено. На малюнку c показана версія графіка абсолютних значень, яка була зрушена так, що його мінімум знаходиться в квадранті I з x = c. Зазначається, що f' (c) не визначено. На малюнку d показана версія функції f (x) = x^3, яка була зрушена так, що точка її перегину знаходиться в квадранті I з x = c, її точка перегину в (c, f (c)) має горизонтальну лінію через неї, і зазначається, що f' (c) = 0. На малюнку e показана версія функції f (x) = x1/3, яка була зрушена так, що точка її перегину знаходиться в квадранті I з x = c, її точка перегину в (c, f (c)) має вертикальну лінію через неї, і зазначається, що f' (c) не визначена. — Рисунок\(\PageIndex{4}\): (a—e) Функція\(f\) має критичну точку,\(c\) якщо\(f'(c)=0\) або\(f'(c)\) не визначена. Функція може мати або не мати локальний екстремум в критичній точці.

Далі в цьому розділі ми розглянемо аналітичні методи визначення того, чи дійсно функція має локальний екстремум у критичній точці. А поки звернемо увагу на пошук критичних точок. Ми будемо використовувати графічні спостереження, щоб визначити, чи пов'язана критична точка з локальним екстремумом.

Приклад\(\PageIndex{1}\): Locating Critical Points

Для кожної з наступних функцій знайдіть всі критичні точки. Використовуйте утиліту графіків, щоб визначити, чи має функція локальний екстремум у кожній з критичних точок.

\(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
\(f(x)=(x^2−1)^3\)
\(f(x)=\frac{4x}{1+x^2}\)

Рішення

а Похідна\(f'(x)=x^2−5x+4\) визначається для всіх дійсних чисел\(x\). Тому нам потрібно лише знайти значення для\(x\) where\(f'(x)=0\). Оскільки\(f'(x)=x^2−5x+4=(x−4)(x−1)\), критичні точки є\(x=1\) і\(x=4.\) з графіка на\(f\) малюнку\(\PageIndex{5}\), ми бачимо, що\(f\) має локальний максимум at\(x=1\) і локальний мінімум при\(x=4\).

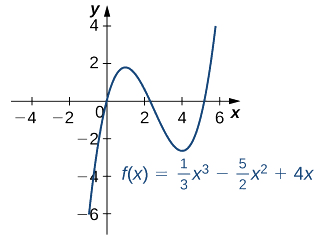
Функція f (x) = (1/3) x^3 — (5/2) x^2+ 4x графічно. Функція має локальний максимум при x = 1 і локальний мінімум при x = 4. — Малюнок\(\PageIndex{5}\): Ця функція має локальний максимум і локальний мінімум.

b Використовуючи правило ланцюга, ми бачимо похідну

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

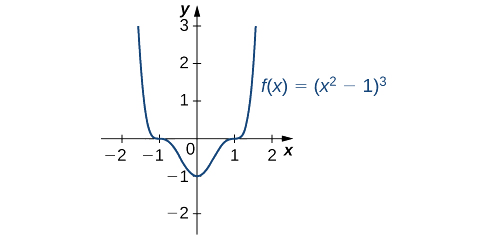
Тому\(f\) має критичні моменти, коли\(x=0\) і коли\(x^2−1=0\). Робимо висновок, що критичні точки є\(x=0,±1\). З графіка на\(f\) малюнку ми бачимо\(\PageIndex{6}\), що\(f\) має локальний (і абсолютний) мінімум на\(x=0\), але не має локального екстремуму при\(x=1\) або\(x=−1\).

Графічна функція f (x) = (x^2 − 1) 3. Функція має локальний мінімум при x = 0, а точки перегину x = ± 1. — Малюнок\(\PageIndex{6}\): Ця функція має три критичні точки:\(x=0\),\(x=1\), і\(x=−1\). Функція має локальний (і абсолютний) мінімум при\(x=0\), але не має крайності в двох інших критичних точках.

c. за частним правилом ми бачимо, що похідна

\(f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

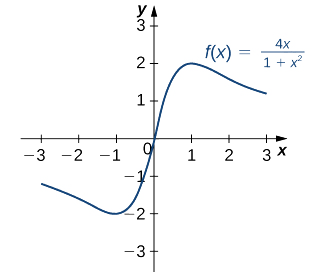
Похідна визначається всюди. Тому нам потрібно лише знайти значення для\(x\) where\(f'(x)=0\). Вирішуючи\(f'(x)=0\), ми бачимо те,\(4−4x^2=0,\) що має на увазі\(x=±1\). Тому критичні точки є\(x=±1\). З графіка на\(f\) малюнку ми бачимо\(\PageIndex{7}\), що f має абсолютний максимум at\(x=1\) і абсолютний мінімум при\(x=−1.\) Отже,\(f\) має локальний максимум at\(x=1\) і локальний мінімум at\(x=−1\). (Зверніть увагу, що якщо\(f\) має абсолютний екстремум протягом інтервалу\(I\) в точці\(c\), яка не є кінцевою точкою\(I\), то\(f\) має локальний екстремум в\(c.)\)

Функція f (x) = 4x/ (1 + x ^ 2) графічна. Функція має локальну/абсолютний максимум при x = 1 і локальний/абсолютний мінімум при x = −1. — Малюнок\(\PageIndex{7}\): Ця функція має абсолютний максимум і абсолютний мінімум.

Вправа\(\PageIndex{1}\)

Знайти всі критичні точки для\(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Підказка: Обчисліть\(f'(x).\)

Відповідь: \(x=\frac{−2}{3}, x=1\)

Розташування Абсолютна Екстрема

Теорема про екстремальні значення стверджує, що неперервна функція на замкнутому обмеженому інтервалі має абсолютний максимум і абсолютний мінімум. Як показано на малюнку\(\PageIndex{2}\), одна або обидві ці абсолютні крайності можуть виникнути в кінцевій точці. Однак, якщо абсолютний екстремум не виникає в кінцевій точці, він повинен відбуватися у внутрішній точці, і в цьому випадку абсолютний екстремум є локальним екстремумом. Тому за теоремою Ферма точка,\(c\) в якій відбувається локальний екстремум, повинна бути критичною точкою. Підсумовуємо цей результат в наступній теоремі.

Теорема\(\PageIndex{3}\): Location of Absolute Extrema

\(f\)Дозволяти бути безперервна функція протягом замкнутого, обмеженого інтервалу\(I\). Абсолютний максимум\(f\) перевищення\(I\) і абсолютний мінімум\(f\) перевищення\(I\) повинні відбуватися в кінцевих точках\(I\) або в критичних точках\(f\) in\(I\).

Маючи на увазі цю ідею, давайте розглянемо процедуру локалізації абсолютних екстремумів.

Стратегія вирішення проблем: визначення абсолютних екстремумів через замкнутий інтервал

Розглянемо неперервну функцію,\(f\) визначену через замкнутий інтервал\([a,b].\)

Оцініть\(f\) в кінцевих точках\(x=a\) і\(x=b.\)
Знайти всі критичні точки\(f\), що лежать протягом інтервалу\((a,b)\) і оцінити\(f\) в цих критичних точках.
Порівняйте всі значення, знайдені в (1) і (2). З «Розташування Абсолютної Екстреми» абсолютна крайність повинна відбуватися в кінцевих точках або критичних точках. Тому найбільшим з цих значень є абсолютний максимум\(f\). Найменшим з цих значень є абсолютний мінімум\(f\).

Тепер давайте розглянемо, як використовувати цю стратегію, щоб знайти абсолютний максимум і абсолютний мінімум для неперервних функцій.

Приклад\(\PageIndex{2}\): Locating Absolute Extrema

Для кожної з наступних функцій знайдіть абсолютний максимум і абсолютний мінімум за вказаний інтервал і стан, де ці значення відбуваються.

\(f(x)=−x^2+3x−2\)над\([1,3].\)
\(f(x)=x^2−3x^{2/3}\)над\([0,2]\).

Рішення

а. крок 1. Оцініть\(f\) в кінцевих точках\(x=1\) і\(x=3\).

\(f(1)=0\)і\(f(3)=−2\)

Крок 2. Оскільки\(f'(x)=−2x+3, f'\) визначається для всіх дійсних чисел\(x.\) Тому немає критичних точок, де похідна не визначена. Залишилося перевірити де\(f'(x)=0\). Так як\(f'(x)=−2x+3=0 \) в\(x=\frac{3}{2}\) і\(\frac{3}{2}\) знаходиться в інтервалі\([1,3], f(\frac{3}{2})\) є кандидатом на абсолютний екстремум\(f\) над\([1,3]\). Оцінюємо\(f(\frac{3}{2})\) і знаходимо

\(f\left(\frac{3}{2}\right)=\frac{1}{4}\).

Крок 3. Ми створили наступну таблицю для порівняння значень, знайдених в кроках 1 і 2.

\(x\)	\(f(x)\)	Висновок
\(1\)	\(0\)
\(\frac{3}{2}\)	\(\frac{1}{4}\)	Абсолютний максимум
\(3\)	\(−2\)	Абсолютний мінімум

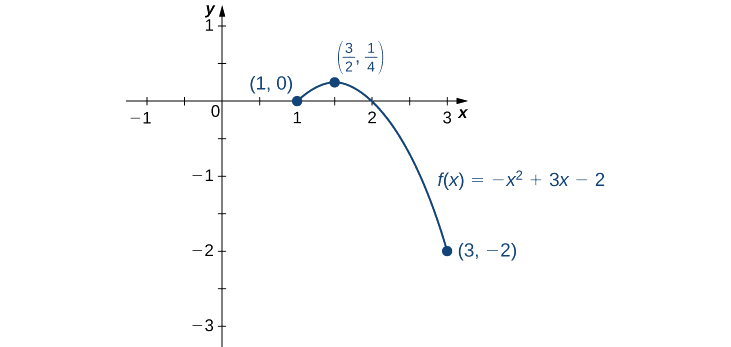
З таблиці ми знаходимо, що абсолютний максимум\(f\) через інтервал [1, 3] є\(\frac{1}{4}\), і це відбувається при\(x=\frac{3}{2}\). Абсолютний мінімум\(f\) над інтервалом\([1, 3]\) дорівнює\(−2\), і він виникає при тому,\(x=3\) як показано на малюнку\(\PageIndex{8}\).

Функція f (x) = — x^2+ 3x — 2 графічна від (1, 0) до (3, −2), причому її максимум позначено у (3/2, 1/4). — Малюнок\(\PageIndex{8}\): Ця функція має як абсолютний максимум, так і абсолютний мінімум.

б. крок 1. Оцініть\(f\) в кінцевих точках\(x=0\) і\(x=2\).

\(f(0)=0\)і\(f(2)=4−3\left(2\right)^{2/3}≈−0.762\)

Крок 2. \(f\)Похідне від дається

\(f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}\)

для\(x≠0\). Похідна дорівнює нулю коли\(2x^{4/3}−2=0\), що має на увазі\(x=±1\). Похідна невизначена при\(x=0\). Тому критичними точками\(f\) є\(x=0,1,−1\). Точка\(x=0\) є кінцевою точкою, тому ми вже оцінювали на\(f(0)\) кроці 1. \(x=−1\)Справа не в інтервалі, що цікавить, тому нам потрібно тільки оцінити\(f(1)\). Ми знаходимо, що

\(f(1)=−2.\)

Крок 3. Ми порівнюємо значення, знайдені в кроках 1 і 2, в наступній таблиці.

\(x\)	\(f(x)\)	Висновок
\(0\)	\(0\)	Абсолютний максимум
\(1\)	\(−2\)	Абсолютний мінімум
\(2\)	\(−0.762\)

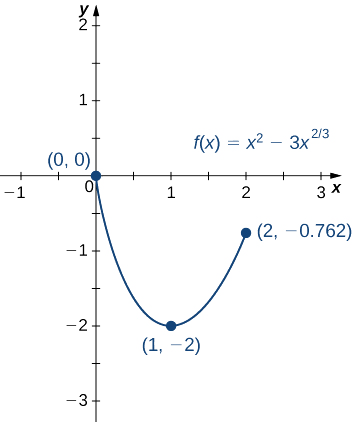
Робимо висновок, що абсолютний максимум\(f\) над інтервалом\([0, 2]\) дорівнює нулю, і він виникає при\(x=0\). Абсолютний мінімум є\(−2,\) і він відбувається при\(x=1\) як показано на малюнку\(\PageIndex{9}\).

Функція f (x) = x^2 — 3x^ (2/3) складається з графіків від (0, 0) до (2, −0,762), її мінімум позначено у (1, −2). — Рисунок\(\PageIndex{9}\): Ця функція має абсолютний максимум в кінцевій точці інтервалу.

Вправа\(\PageIndex{2}\)

Знайти абсолютний максимум і абсолютний мінімум\(f(x)=x^2−4x+3\) за інтервал\([1,4]\).

Підказка: Шукайте критичні точки. Оцінюйте\(f\) у всіх критичних точках і в кінцевих точках.

Відповідь: Абсолютний максимум є\(3\) і відбувається він при\(x=4\). Абсолютний мінімум є\(−1\) і відбувається він при\(x=2\).

На даний момент ми знаємо, як знайти абсолютні екстремуми для безперервних функцій через замкнуті проміжки часу. Ми також визначили локальну екстрему і визначили, що якщо функція\(f\) має локальний екстремум в точці\(c\), то\(c\) повинна бути критичною точкою\(f\). Однак\(c\) бути критичною точкою не є достатньою умовою для того,\(f\) щоб мати локальний екстремум при\(c\). Пізніше в цьому розділі ми покажемо, як визначити, чи дійсно функція має локальний екстремум у критичній точці. Однак спочатку нам потрібно ввести теорему про середнє значення, яка допоможе нам аналізувати поведінку графа функції.

Ключові поняття

Функція може мати як абсолютний максимум, так і абсолютний мінімум, мати лише один абсолютний екстремум або не мати абсолютного максимуму або абсолютного мінімуму.
Якщо функція має локальний екстремум, точка, в якій вона виникає, повинна бути критичною точкою. Однак функція не повинна мати локальний екстремум в критичній точці.
Неперервна функція на замкнутому обмеженому інтервалі має абсолютний максимум і абсолютний мінімум. Кожен екстремум виникає в критичній точці або кінцевій точці.

Глосарій

абсолютний екстремум: якщо\(f\) має абсолютний максимум або абсолютний мінімум на\(c\), ми говоримо,\(f\) має абсолютний екстремум при\(c\)

абсолютний максимум: якщо\(f(c)≥f(x)\) для всіх\(x\) в області\(f\), ми говоримо,\(f\) має абсолютний максимум при\(c\)

абсолютний мінімум: якщо\(f(c)≤f(x)\) для всіх\(x\) в домені\(f\), ми говоримо,\(f\) має абсолютний мінімум на\(c\)

критична точка: якщо\(f'(c)=0\) або\(f'(c)\) не визначено, ми говоримо, що c є критичною точкою\(f\)

теорема про екстремальне значення: якщо\(f\) є безперервною функцією над скінченним замкнутим інтервалом, то\(f\) має абсолютний максимум і абсолютний мінімум

Теорема Ферма: якщо\(f\) має локальний екстремум в\(c\), то\(c\) є критичною точкою\(f\)

локальний екстремум: якщо\(f\) має локальний максимум або локальний мінімум на\(c\), ми говоримо,\(f\) має локальний екстремум в\(c\)

локальний максимум: якщо існує інтервал\(I\) такий, що\(f(c)≥f(x)\) для всіх\(x∈I\), ми говоримо\(f\) має локальний максимум при\(c\)

місцевий мінімум: якщо існує інтервал\(I\) такий, що\(f(c)≤f(x)\) для всіх\(x∈I\), ми говоримо\(f\) має локальний мінімум на\(c\)