4.10: Антипохідні
- Page ID
- 62190
- Знайдіть загальне антипохідне заданої функції.
- Поясніть терміни і позначення, що використовуються для невизначеного інтеграла.
- Створіть правило потужності для інтегралів.
- Використовуйте антидиференціювання для вирішення простих початкових задач.
На цьому етапі ми бачили, як обчислити похідні багатьох функцій, і були ознайомлені з різноманітними їх застосуваннями. Тепер ми задаємо питання, яке обертає цей процес навколо: З огляду на функцію\(f\), як ми знаходимо функцію з похідною\(f\) і чому б нас зацікавила така функція?
На першу частину цього питання ми відповідаємо визначенням антипохідних. Антипохідне функції\(f\) - це функція з похідною\(f\). Чому нас цікавлять антипохідні? Потреба в антипохідних виникає в багатьох ситуаціях, і ми розглядаємо різні приклади по всій решті тексту. Тут ми розглянемо один конкретний приклад, який передбачає прямолінійний рух. У нашому дослідженні в похідних прямолінійного руху ми показали, що якщо задати позиційну функцію\(s(t)\) об'єкта, то його\(v(t)\) швидкісна функція є похідною від\(s(t)\) —тобто\(v(t)=s′(t)\). Крім того, прискорення\(a(t)\) є похідною від швидкості\(v(t)\) - тобто\(a(t)=v′(t)=s''(t)\). Тепер припустимо, нам дана функція прискорення\(a\), але не функція швидкості\(v\) або функція положення\(s\). Так як\(a(t)=v′(t)\) визначення швидкісної функції вимагає від нас знайти антипохідну від функції прискорення. Тоді, оскільки\(v(t)=s′(t),\) визначення функції положення вимагає від нас знайти антипохідну швидкісної функції. Прямолінійний рух - всього лише один випадок, в якому виникає потреба в антипохідних. Ми побачимо ще багато прикладів у решті тексту. А поки давайте розглянемо термінологію і позначення для антипохідних, а також визначимо антипохідні для декількох типів функцій. Розглянуто різні методи пошуку антипохідних більш складних функцій далі в тексті (Вступ до методів інтеграції).
Реверс диференціації
На цьому етапі ми знаємо, як знайти похідні різних функцій. Тепер ми задаємо протилежне питання. Задано функцію\(f\), як знайти функцію з похідною\(f\)? Якщо ми можемо знайти функцію\(F\) з похідною,\(f,\) ми викликаємо\(F\) антипохідну від\(f\).
Функція\(F\) є антипохідною функції,\(f\) якщо
\[F′(x)=f(x) \nonumber \]
для всіх\(x\) у домені\(f\).
Розглянемо функцію\(f(x)=2x\). Знаючи силове правило диференціації, робимо висновок, що\(F(x)=x^2\) є антипохідним від\(f\) since\(F′(x)=2x\).
Чи існують інші антипохідні\(f\)?
Так; оскільки похідна будь-якої константи\(C\) дорівнює нулю, також\(x^2+C\) є антипохідним від\(2x\). Тому\(x^2+5\) і\(x^2−\sqrt{2}\) є також антипохідними.
Чи є інші, які не мають форми\(x^2+C\) для якоїсь постійної\(C\)?
Відповідь - ні. З наслідок 2 теореми про середнє значення ми знаємо, що якщо\(F\) і\(G\) є диференційованими функціями, такими, що\(F′(x)=G′(x),\) тоді\(F(x)−G(x)=C\) для деякої константи\(C\). Цей факт призводить до наступної важливої теореми.
\(F\)Дозволяти бути антипохідним\(f\) над інтервалом\(I\). Потім,
- для кожної\(C\) константи функція також\(F(x)+C\) є антипохідним від\(f\) над\(I\);
- якщо\(G\) є антипохідним\(f\) над\(I\), є постійна\(C\) для якої\(G(x)=F(x)+C\) понад\(I\).
Іншими словами, найбільш загальною формою антипохідного\(f\) над\(I\) є\(F(x)+C\).
Ми використовуємо цей факт і наші знання похідних, щоб знайти всі антипохідні для декількох функцій.
Для кожної з перерахованих нижче функцій знайдіть всі антипохідні.
- \(f(x)=3x^2\)
- \(f(x)=\dfrac{1}{x}\)
- \(f(x)=\cos x\)
- \(f(x)=e^x\)
Рішення:
а. тому що
\[\dfrac{d}{dx}\left(x^3\right)=3x^2 \nonumber \]
то\(F(x)=x^3\) є антипохідним від\(3x^2\). Тому кожне\(3x^2\) антипохідне має форму\(x^3+C\) для якоїсь постійної\(C\), і кожна функція форми\(x^3+C\) є антипохідним від\(3x^2\).
б. нехай\(f(x)=\ln |x|.\)
Для\(x>0,\; f(x)=\ln |x|=\ln (x)\) і
\[\dfrac{d}{dx}\Big(\ln x\Big)=\dfrac{1}{x}. \nonumber \]
Для\(x<0,\; f(x)=\ln |x|=\ln (−x)\) і
\[\dfrac{d}{dx}\Big(\ln (−x)\Big)=−\dfrac{1}{−x}=\dfrac{1}{x}. \nonumber \]
Тому
\[\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}. \nonumber \]
Таким чином,\(F(x)=\ln |x|\) є антипохідним від\(\dfrac{1}{x}\). Тому кожне\(\dfrac{1}{x}\) антипохідне має форму\(\ln |x|+C\) для якоїсь постійної,\(C\) і кожна функція форми\(\ln |x|+C\) є антипохідним від\(\dfrac{1}{x}\).
c У нас є
\[\dfrac{d}{dx}\Big(\sin x\Big)=\cos x, \nonumber \]
так\(F(x)=\sin x\) є антипохідним від\(\cos x\). Тому кожне\(\cos x\) антипохідне має форму\(\sin x+C\) для якоїсь постійної,\(C\) і кожна функція форми\(\sin x+C\) є антипохідним від\(\cos x\).
d. з тих пір
\[\dfrac{d}{dx}\left(e^x\right)=e^x, \nonumber \]
то\(F(x)=e^x\) є антипохідним від\(e^x\). Тому кожне\(e^x\) антипохідне має форму\(e^x+C\) для якоїсь постійної,\(C\) і кожна функція форми\(e^x+C\) є антипохідним від\(e^x\).
Знайти всі антипохідні\(f(x)=\sin x\).
- Підказка
-
Яку функцію має похідна\(\sin x\)?
- Відповідь
-
\(F(x) = −\cos x+C\)
Невизначені інтеграли
Тепер ми розглянемо формальні позначення, що використовуються для представлення антипохідних, і розглянемо деякі їх властивості. Ці властивості дозволяють знайти антипохідні більш складних функцій. Задано функцію\(f\), ми використовуємо позначення\(f′(x)\) або\(\dfrac{df}{dx}\) для позначення похідної від\(f\). Тут ми вводимо позначення для антипохідних. Якщо\(F\) є антипохідним від\(f\), ми говоримо, що\(F(x)+C\) це найбільш загальне антипохідне\(f\) і писати
\[\int f(x)\,dx=F(x)+C.\nonumber \]
Символ\(\displaystyle \int \) називається цілісним знаком, і\(\displaystyle \int f(x)\,dx\) називається невизначений інтеграл\(f\).
Задана функція\(f\), невизначений інтеграл\(f\), позначається
\[\int f(x)\,dx, \nonumber \]
є найбільш загальним антипохідним від\(f\). Якщо\(F\) є антипохідним від\(f\), то
\[\int f(x)\,dx=F(x)+C. \nonumber \]
Вираз\(f(x)\) називається integrand, а змінна\(x\) є змінною інтеграції.
З огляду на термінологію, введену в це визначення, акт знаходження антипохідних функції зазвичай\(f\) називають інтегруючим\(f\).
Для функції\(f\) та\(F\) антидериватива функції\(F(x)+C\), де\(C\) є будь-яке дійсне число, часто називають сімейством антипохідних\(f\). Наприклад, оскільки\(x^2\) є антипохідним\(2x\) і будь-яке антипохідне від\(2x\) - форми, яку\(x^2+C,\) ми пишемо
\[\int 2x\,dx=x^2+C.\nonumber \]
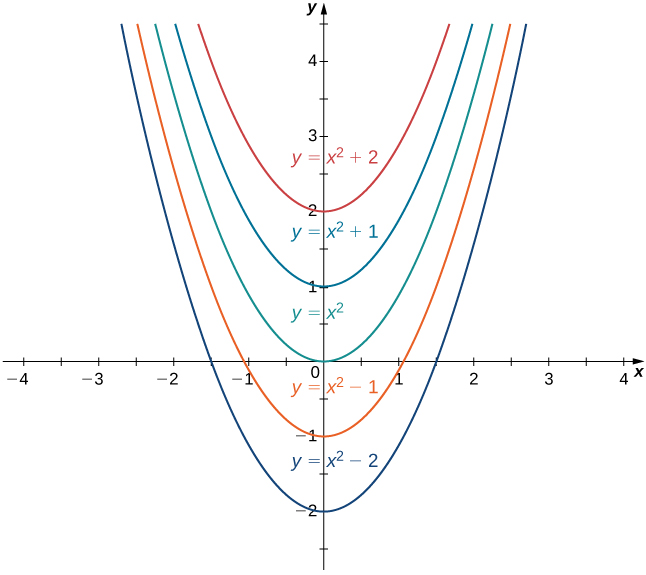
Колекція всіх функцій виду,\(x^2+C,\) де\(C\) знаходиться будь-яке дійсне число, відома як сімейство антипохідних\(2x\). \(\PageIndex{1}\)На малюнку показаний графік цього сімейства антипохідних.
Для деяких функцій оцінка невизначеного інтегралу випливає безпосередньо з властивостей похідних. Наприклад, для\(n≠−1\),
\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C,\)
який надходить безпосередньо з
\(\dfrac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n\).
Цей факт відомий як правило потужності для інтегралів.
Для\(n≠−1,\)
\[\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C. \nonumber \]
Оцінка невизначеного інтегралу для деяких інших функцій також є простим обчисленням. У наступній таблиці наведено невизначені інтеграли для декількох загальних функцій. Більш повний список відображається в Додатку B.
| Формула диференціації | невизначений інтеграл |
|---|---|
| \(\dfrac{d}{dx}\Big(k\Big)=0\) | \(\displaystyle \int k\,dx=\int kx^0\,dx=kx+C\) |
| \(\dfrac{d}{dx}\Big(x^n\Big)=nx^{n−1}\) | \(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C\)для\(n≠−1\) |
| \(\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}\) | \(\displaystyle \int \dfrac{1}{x}\,dx=\ln |x|+C\) |
| \(\dfrac{d}{dx}\Big(e^x\Big)=e^x\) | \(\displaystyle \int e^x\,dx=e^x+C\) |
| \(\dfrac{d}{dx}\Big(\sin x\Big)=\cos x\) | \(\displaystyle \int \cos x\,dx=\sin x+C\) |
| \(\dfrac{d}{dx}\Big(\cos x\Big)=−\sin x\) | \(\displaystyle \int \sin x\,dx=−\cos x+C\) |
| \(\dfrac{d}{dx}\Big(\tan x\Big)=\sec^2 x\) | \(\displaystyle \int \sec^2 x\,dx=\tan x+C\) |
| \(\dfrac{d}{dx}\Big(\csc x\Big)=−\csc x\cot x\) | \(\displaystyle \int \csc x\cot x\,dx=−\csc x+C\) |
| \(\dfrac{d}{dx}\Big(\sec x\Big)=\sec x\tan x\) | \(\displaystyle \int \sec x\tan x\,dx=\sec x+C\) |
| \(\dfrac{d}{dx}\Big(\cot x\Big)=−\csc^2 x\) | \(\displaystyle \int \csc^2x\,dx=−\cot x+C\) |
| \(\dfrac{d}{dx}\Big(\sin^{−1}x\Big)=\dfrac{1}{\sqrt{1−x^2}}\) | \(\displaystyle \int \dfrac{1}{\sqrt{1−x^2}}=\sin^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\tan^{−1}x\Big)=\dfrac{1}{1+x^2}\) | \(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\tan^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\sec^{−1}|x|\Big)=\dfrac{1}{x\sqrt{x^2−1}}\) | \(\displaystyle \int \dfrac{1}{x\sqrt{x^2−1}}\,dx=\sec^{−1}|x|+C\) |
З визначення невизначеного інтеграла\(f\), ми знаємо
\[\int f(x)\,dx=F(x)+C\nonumber \]
якщо і тільки якщо\(F\) є антипохідним від\(f\).
Тому, стверджуючи, що
\[\int f(x)\,dx=F(x)+C\nonumber \]
важливо перевірити, чи правильно це твердження, перевіривши, що\(F′(x)=f(x).\)
Кожен з наступних тверджень має форму\(\displaystyle \int f(x)\,dx=F(x)+C.\) Переконайтеся, що кожне твердження є правильним, показуючи, що\(F′(x)=f(x).\)
- \(\displaystyle\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C\)
- \(\displaystyle\int xe^x\,dx=xe^x−e^x+C\)
Рішення:
а. з тих пір
\(\dfrac{d}{dx}\left(\dfrac{x^2}{2}+e^x+C\right)=x+e^x\),
заяву
\[\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C \nonumber \]
є правильним.
Зауважте, що ми перевіряємо невизначений інтеграл для суми. Крім того,\(\dfrac{x^2}{2}\) і\(e^x\) є антипохідними\(x\) і\(e^x\), відповідно, і сума антипохідних є антипохідним від суми. Цей факт ми ще раз обговоримо пізніше в цьому розділі.
б Використовуючи правило продукту, ми бачимо, що
\[\dfrac{d}{dx}\left(xe^x−e^x+C\right)=e^x+xe^x−e^x=xe^x. \nonumber \]
Тому заяву
\[\int xe^x\,dx=xe^x−e^x+C \nonumber \]
є правильним.
Зверніть увагу, що ми перевіряємо невизначений інтеграл для продукту. Антидериватив не\(xe^x−e^x\) є продуктом антипохідних. Крім того, продукт антипохідних, не\(x^2e^x/2\) є антипохідним\(xe^x\) з тих пір
\(\dfrac{d}{dx}\left(\dfrac{x^2e^x}{2}\right)=xe^x+\dfrac{x^2e^x}{2}≠xe^x\).
Взагалі, продукт антипохідних не є антипохідним продукту.
Переконайтеся, що\(\displaystyle \int x\cos x\,\,dx=x\sin x+\cos x+C.\)
- Підказка
-
Розрахувати\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big).\)
- Відповідь
-
\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big)=\sin x+x\cos x−\sin x=x \cos x\)
У таблиці\(\PageIndex{1}\) ми перерахували невизначені інтеграли для багатьох елементарних функцій. Давайте тепер звернемо увагу на оцінку невизначені інтеграли для більш складних функцій. Наприклад, розглянемо знаходження антидериватива від суми\(f+g\). У прикладі\(\PageIndex{2}a\) ми показали, що антидериватив суми\(x+e^x\) задається сумою\(\dfrac{x^2}{2}+e^x\) —тобто антипохідне від суми задається сумою антипохідних. Цей результат не був специфічним для цього прикладу. Взагалі, якщо\(F\) і\(G\) є антипохідними будь-яких функцій\(f\) і\(g\), відповідно, то
\(\dfrac{d}{dx}\big(F(x)+G(x)\big)=F′(x)+G′(x)=f(x)+g(x).\)
Тому\(F(x)+G(x)\) є антипохідним від\(f(x)+g(x)\) і у нас
\[ \int \big(f(x)+g(x)\big)\,dx=F(x)+G(x)+C.\nonumber \]
Аналогічно,
\[ \int \big(f(x)−g(x)\big)\,dx=F(x)−G(x)+C.\nonumber \]
Крім того, розглянемо завдання знаходження антидериватива від того,\(kf(x),\) де\(k\) знаходиться будь-яке дійсне число. Так як
\[ \dfrac{d}{dx}\Big(kF(x)\Big)=k\dfrac{d}{dx}\Big(F(x)\Big)=kF′(x)\nonumber \]
для будь-якого дійсного числа робимо висновок\(k\), що
\[ \int kf(x)\,dx=kF(x)+C.\nonumber \]
Ці властивості підсумовуються далі.
\(F\)\(G\)Дозволяти і бути антипохідними\(f\) і\(g\), відповідно, і нехай\(k\) буде будь-яке дійсне число.
Суми та відмінності
\[\int \big(f(x)±g(x)\big)\,dx=F(x)±G(x)+C \nonumber \]
Постійні кратні
\[ \int kf(x)\,dx=kF(x)+C \nonumber \]
З цієї теореми ми можемо оцінити будь-який інтеграл, що включає суму, різницю або постійну кратну функцій з відомими антипохідними. Оцінка інтегралів за участю продуктів, коефіцієнтів або композицій є більш складною. (Див. Приклад\(\PageIndex{2}b\) для прикладу, пов'язаного з антипохідним продукту.) Ми розглядаємо та розглядаємо інтеграли, що включають ці більш складні функції у Вступ до інтеграції. У наступному прикладі ми розглянемо, як використовувати цю теорему для обчислення невизначеного інтегралу декількох функцій.
Оцініть кожен з наступних невизначений інтегралів:
- \(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx\)
- \(\displaystyle \int \dfrac{x^2+4\sqrt[3]{x}}{x}\,dx\)
- \(\displaystyle \int \dfrac{4}{1+x^2}\,dx\)
- \(\displaystyle \int \tan x\cos x\,dx\)
Рішення:
а Використовуючи властивості невизначеного інтегралу, ми можемо інтегрувати кожен з чотирьох членів у ціле окремо. Отримуємо
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx.\)
З другої частини Властивості невизначеного інтегралів кожен коефіцієнт можна записати перед знаком інтеграла, який дає
\(\displaystyle \int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx=5\int x^3\,dx−7\int x^2\,dx+3\int x\,dx+4\int 1\,dx.\)
Використовуючи правило потужності для інтегралів, робимо висновок, що
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\dfrac{5}{4}x^4−\dfrac{7}{3}x^3+\dfrac{3}{2}x^2+4x+C.\)
b. перепишіть цілісний як
\(\dfrac{x^2+4\sqrt[3]{x}}{x}=\dfrac{x^2}{x}+\dfrac{4\sqrt[3]{x}}{x}.\)
Потім, щоб оцінити інтеграл, інтегруйте кожен з цих термінів окремо. Використовуючи правило харчування, ми маємо
\ [\ почати {вирівнювати*}\ int\ вліво (x+\ dfrac {4} {x^ {2/3}}\ праворуч)\, dx&=\ int x\, dx+4\ int x^ {−2/3}\, dx\\ [4pt]
&=\ dfrac {1} {2} x^2+4\ dfrac {1} {\ ліворуч (\ tfrac {−−2} {3}\ праворуч) +1} x^ {(−2/3) +1} +C\\ [4pt]
&=\ dfrac {1} {2} x^2+12x^ {1/3} +C.\ end {align*}\]
c Використовуючи властивості невизначеного інтегралу, запишіть інтеграл як
\(4\displaystyle \int \dfrac{1}{1+x^2}\,dx.\)
Потім використовуйте той факт, що\(\tan^{−1}(x)\) є антипохідним,\(\dfrac{1}{1+x^2}\) щоб зробити висновок, що
\(\displaystyle \int \dfrac{4}{1+x^2}\,dx=4\tan^{−1}(x)+C.\)
d. перепишіть integrand як
\(\tan x\cos x=\dfrac{\sin x}{\cos x}\cdot\cos x=\sin x.\)
Тому
\(\displaystyle \int \tan x\cos x\,dx=\int \sin x\,dx=−\cos x+C.\)
Оцініть\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx\).
- Підказка
-
Інтегруйте кожен термін в integrand окремо, використовуючи правило влади.
- Відповідь
-
\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx = \quad x^4−\dfrac{5}{3}x^3+\dfrac{1}{2}x^2−7x+C\)
Проблеми початкового значення
Ми розглядаємо методи інтеграції великої різноманітності функцій за участю продуктів, коефіцієнтів та композицій пізніше в тексті. Тут ми звернемося до одного поширеного використання антипохідних, яке виникає часто в багатьох додатках: розв'язування диференціальних рівнянь.
Диференціальне рівняння - це рівняння, яке пов'язує невідому функцію і одну або кілька її похідних. рівняння
простий приклад диференціального рівняння. Рішення цього рівняння означає знаходження функції\(y\) з похідною\(f\). Тому розв'язки рівняння\ ref {diffeq1} є антипохідними\(f\). Якщо\(F\) є одним антипохідним від\( f\), кожна функція форми\( y=F(x)+C\) є розв'язком цього диференціального рівняння. Наприклад, рішення
даються
Іноді ми зацікавлені у визначенні того, чи проходить певна крива рішення через певну точку\( (x_0,y_0)\) —тобто\( y(x_0)=y_0\). Задача про знаходження функції,\(y\) що задовольняє диференціальне рівняння
з додатковою умовою
є прикладом задачі початкового значення. Стан\( y(x_0)=y_0\) відомий як початкова умова. Наприклад, шукаємо функцію,\( y\) яка задовольняє диференціальному рівнянню
і початкова умова
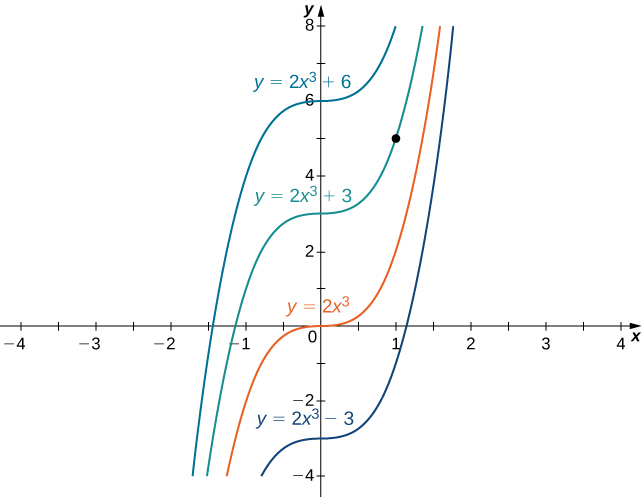
є прикладом задачі початкового значення. Оскільки розв'язки диференціального рівняння полягають в тому,\( y=2x^3+C,\) щоб знайти функцію,\(y\) яка також задовольняє початковій умові, нам потрібно знайти\(C\) таку, що\(y(1)=2(1)^3+C=5\). З цього рівняння ми бачимо це\( C=3\), і робимо висновок, що\( y=2x^3+3\) це рішення цієї початково-значної задачі, як показано на наступному графіку.
Вирішити задачу початкового значення
\[\dfrac{dy}{dx}=\sin x,\quad y(0)=5.\nonumber \]
Рішення
Для початку нам потрібно вирішити диференціальне рівняння. Якщо\(\dfrac{dy}{dx}=\sin x\), то
\[y=\displaystyle \int \sin(x)\,dx=−\cos x+C.\nonumber \]
Далі потрібно шукати рішення\(y\), яке задовольняє початковій умові. Початкова умова\(y(0)=5\) означає, що нам потрібна постійна\(C\) така, що\(−\cos x+C=5.\) Тому,
\[C=5+\cos(0)=6.\nonumber \]
Рішення початково-значущої задачі полягає в\(y=−\cos x+6.\)
Вирішити початкову задачу значення\(\dfrac{dy}{dx}=3x^{−2},\quad y(1)=2\).
- Підказка
-
Знайти всі антипохідні\(f(x)=3x^{−2.}\)
- Відповідь
-
\(y=−\dfrac{3}{x}+5\)
Проблеми з початковим значенням виникають у багатьох додатках. Далі розглянемо проблему, при якій водій застосовує гальма в автомобілі. Нас цікавить, скільки часу потрібно для зупинки автомобіля. Нагадаємо, що функція швидкості\(v(t)\) є похідною від функції положення,\(s(t),\) а\(a(t)\) прискорення - похідна від функції швидкості. У попередніх прикладах у тексті ми могли обчислити швидкість з позиції, а потім обчислити прискорення від швидкості. У наступному прикладі ми працюємо навпаки. З огляду на функцію прискорення, обчислюємо функцію швидкості. Потім ми використовуємо функцію швидкості для визначення функції положення.
Автомобіль їде зі швидкістю\(88\) ft/sec (\(60\)mph) при застосуванні гальм. Автомобіль починає сповільнюватися з постійною швидкістю\(15\) ft/sec 2.
- Скільки секунд проходить до зупинки автомобіля?
- Як далеко проїжджає автомобіль за цей час?
Рішення
а. спочатку ми вводимо змінні для цієї задачі. \(t\)Дозволяти час (в секундах) після першого застосування гальм. \(a(t)\)Дозволяти бути прискорення автомобіля (в футах на секунди в квадраті) в часі\(t\). \(v(t)\)Дозволяти швидкість автомобіля (в футах в секунду) в той час\(t\). \(s(t)\)Дозволяти положення автомобіля (в ногах) за межами точки, де гальма застосовуються в той час\(t\).
Автомобіль їде зі швидкістю\(88\) ft/sec. Тому початкова швидкість -\(v(0)=88\) фут/сек. Так як автомобіль гальмує, то розгін
\(a(t)=−15\,\text{ft/sec}^2\).
Прискорення є похідною від швидкості,
\(v′(t)=-15.\)
Тому ми маємо проблему початкового значення, яку потрібно вирішити:
\(v′(t)=−15,\quad v(0)=88.\)
Інтегруючи, ми виявляємо, що
\(v(t)=−15t+C.\)
Так як\(v(0)=88,C=88.\) Таким чином, функція швидкості
\(v(t)=−15t+88.\)
Щоб дізнатися, скільки часу потрібно для зупинки автомобіля, нам потрібно знайти\(t\) такий час, щоб швидкість була нульовою. Рішення\(−15t+88=0,\) отримуємо\(t=\dfrac{88}{15}\) сек.
б. щоб дізнатися, як далеко проїжджає автомобіль за цей час, нам потрібно знайти положення автомобіля після\(\dfrac{88}{15}\) сек. Ми знаємо, що швидкість\(v(t)\) є похідною від положення\(s(t)\). Розглянемо початкове положення, яке має бути\(s(0)=0\). Тому нам потрібно вирішити початково-вартісну задачу
\(s′(t)=−15t+88,\quad s(0)=0.\)
Інтегруючи, ми маємо
\(s(t)=−\dfrac{15}{2}t^2+88t+C.\)
Так як\(s(0)=0\), константа є\(C=0\). Тому функція положення є
\(s(t)=−\dfrac{15}{2}t^2+88t.\)
Після\(t=\frac{88}{15}\) сек положення\(s\left(\frac{88}{15}\right)≈258.133\) футів.
Припустимо, автомобіль їде зі швидкістю\(44\) ft/sec. Скільки часу потрібно, щоб машина зупинилася? Як далеко проїде автомобіль?
- Підказка
-
\(v(t)=−15t+44.\)
- Відповідь
-
\(2.93\)сек,\(64.5\) фут
Ключові концепції
- Якщо\(F\) є антипохідним від\(f,\) то кожне\(f\) антипохідне має форму\(F(x)+C\) для певної константи\(C\).
- Вирішення початкової задачі\[\dfrac{dy}{dx}=f(x),\quad y(x_0)=y_0 \nonumber \] вимагає від нас спочатку знайти сукупність антипохідних,\(f\) а потім шукати ту конкретну антипохідну, яка також задовольняє початковій умові.
Глосарій
- антидериватив
- функція\(F\) така, що\(F′(x)=f(x)\) для всіх\(x\) в області з\(f\) є антипохідним від\(f\)
- невизначений інтеграл
- найзагальнішим антипохідним від\(f(x)\) є невизначений інтеграл\(f\); ми використовуємо позначення\(\displaystyle \int f(x)\,dx\) для позначення невизначеного інтеграла\(f\)
- завдання початкового значення
- задача, яка вимагає знаходження функції,\(y\) яка задовольняє диференціальне рівняння\(\dfrac{dy}{dx}=f(x)\) разом з початковою умовою\(y(x_0)=y_0\)
