4.8: Правило L'Hôpital

Last updated
Save as PDF

Page ID: 62191

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Визнайте, коли застосовувати правило L'Hôpital.
Визначте невизначені форми, вироблені частками, продуктами, відніманнями та повноваженнями, і застосовуйте правило L'Hôpital у кожному конкретному випадку.
Охарактеризуйте відносні темпи зростання функцій.

У цьому розділі ми розглянемо потужний інструмент оцінки лімітів. Цей інструмент, відомий як правило L'Hôpital, використовує похідні для обчислення лімітів. За допомогою цього правила ми зможемо оцінити багато меж, які ми ще не змогли визначити. Замість того, щоб покладатися на числові докази, щоб здогадатися, що межа існує, ми зможемо остаточно показати, що межа існує, і визначити його точне значення.

Застосування правила L'Hôpital

Правило L'Hôpital може бути використано для оцінки меж, що включають частку двох функцій. Розглянемо

\[\lim_{x→a}\dfrac{f(x)}{g(x)}. \nonumber \]

Якщо\(\displaystyle \lim_{x→a}f(x)=L_1\) і\(\displaystyle \lim_{x→a}g(x)=L_2≠0,\) тоді

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}. \nonumber \]

Однак що станеться, якщо\(\displaystyle \lim_{x→a}f(x)=0\) і\(\displaystyle \lim_{x→a}g(x)=0\)? Ми називаємо це однією з невизначеної форми типу\(\dfrac{0}{0}\). Це вважається невизначеною формою, оскільки ми не можемо визначити точну поведінку\(\dfrac{f(x)}{g(x)}\) як\(x→a\) без подальшого аналізу. Приклади цього ми бачили раніше в тексті. Наприклад, розглянемо

\[\lim_{x→2}\dfrac{x^2−4}{x−2} \nonumber \]

\[\lim_{x→0}\dfrac{\sin x}{x}.\nonumber \]

Для першого з цих прикладів ми можемо оцінити межу шляхом факторингу чисельника і написання

\[\lim_{x→2}\dfrac{x^2−4}{x−2}=\lim_{x→2}\dfrac{(x+2)(x−2)}{x−2}=\lim_{x→2}(x+2)=2+2=4. \nonumber \]

Бо\(\displaystyle \lim_{x→0}\dfrac{\sin x}{x}\) ми змогли показати, використовуючи геометричний аргумент, що

\[\lim_{x→0}\dfrac{\sin x}{x}=1. \nonumber \]

Тут ми використовуємо іншу методику оцінки таких обмежень, як ці. Ця методика не тільки забезпечує простіший спосіб оцінити ці межі, але й, що ще важливіше, вона надає нам спосіб оцінити багато інших обмежень, які ми не могли обчислити раніше.

Ідею, що стоїть за правилом L'Hôpital, можна пояснити за допомогою локальних лінійних наближень. Розглянемо дві диференційовні функції\(f\) і\(g\) такі, що\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) і такі, що\(g′(a)≠0\) Для\(x\)\(a\) ближнього, ми можемо написати

\[f(x)≈f(a)+f′(a)(x−a) \nonumber \]

\[g(x)≈g(a)+g′(a)(x−a). \nonumber \]

Тому,

\[\dfrac{f(x)}{g(x)}≈\dfrac{f(a)+f′(a)(x−a)}{g(a)+g′(a)(x−a)}. \nonumber \]

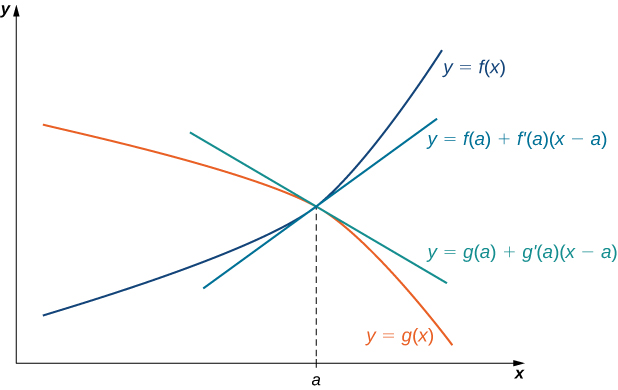
Дві функції y = f (x) і y = g (x) намальовані таким чином, що вони перетинаються у точці вище x = a, а також намальовані лінійні наближення цих двох функцій y = f (a) + f' (a) (x — a) та y = g (a) + g' (a) (x — a). — Малюнок\(\PageIndex{1}\): Якщо\(\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x)\), то відношення приблизно\(f(x)/g(x)\) дорівнює відношенню їх лінійних наближень поблизу\(a\).

Так як\(f\) диференціюється при\(a\), то\(f\) є безперервним при\(a\), і тому\(\displaystyle f(a)=\lim_{x→a}f(x)=0\). Аналогічно,\(\displaystyle g(a)=\lim_{x→a}g(x)=0\). Якщо ми також припустимо, що\(f′\) і\(g′\) є безперервними при\(x=a\), то\(\displaystyle f′(a)=\lim_{x→a}f′(x)\) і\(\displaystyle g′(a)=\lim_{x→a}g′(x)\). Використовуючи ці ідеї, робимо висновок, що

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)(x−a)}{g′(x)(x−a)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} . \nonumber \]

Зверніть увагу, що припущення про те, що\(f′\) і\(g′\) є безперервними при\(a\) і\(g′(a)≠0\) може бути ослаблене. Ми констатуємо правило L'Hôpital формально для невизначеної форми\(\dfrac{0}{0}\). Також зверніть увагу, що позначення не\(\dfrac{0}{0}\) означає, що ми фактично ділимо нуль на нуль. Швидше, ми використовуємо позначення\(\dfrac{0}{0}\) для представлення частки меж, кожен з яких дорівнює нулю.

Правило L'Hôpital (випадок 0/0)

Припустимо\(g\),\(f\) і є диференційованими функціями над відкритим інтервалом\(a\), що містить, крім можливо в\(a\). Якщо\(\displaystyle \lim_{x→a}f(x)=0\) і\(\displaystyle \lim_{x→a}g(x)=0,\) тоді

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, \nonumber \]

припускаючи, що ліміт на право існує або є\(∞\) або\(−∞\). Цей результат також тримається, якщо ми розглядаємо односторонні межі, або якщо\(a=∞\) або\(a=−∞.\)

Доказ

Наведено доказ цієї теореми в окремому випадку, коли\(f,g,f′,\) і\(g′\) всі безперервні протягом відкритого інтервалу, що містять\(a\). У такому випадку, оскільки\(\displaystyle\lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) і\(f\) і\(g\) є безперервними при\(a\), випливає, що\(f(a)=0=g(a)\). Тому,

\ [\ почати {вирівнювати*}\ lim_ {x→a}\ dfrac {f (x)} {g (x)} &=\ lim_ {x→a}\ dfrac {f (x) −f (a)} {g (x) −г (а)} &\ текст {Починаючи з}\, f (a) =0 = г (а)\\ [4pt]
&=\ lim_ {x→a}\ dfrac {\ dfrac {f (x) −f (a)} {x−a}} {\ dfrac {g (x) −g (a)} {x−a}} &\ text {множити чисельник і знаменник на}\,\ frac {1} {x-a}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→a}\ dfrac {f (x) −f (a)} {x−a}} {\ displaystyle\ lim_ {x→a}\ dfrac {g (x) −g (a)} {x−a}} &\ text {Межа частки є часткою обмежень}.\\ [4pt]
&=\ dfrac {f′ (a)} {g′ (a)} &\ text {За визначенням похідної}\\ [4pt]
&=\ розрив {\ стиль відображення\ lim_ {x → a} f′ (x)} {\ стиль відображення\ lim_ {x → a} g′ (x)} &\ текст {За безперервністю}\, f′\,\ text {і}\, g′\\ [4pt]
&=\ lim_ {x → a}\ dfrac {f′ (x) {g′ (x)}. &\ text {Обмеження частки}\ end {align*}\]

Зверніть увагу, що правило L'Hôpital говорить, що ми можемо обчислити межу частки,\(\dfrac{f}{g}\) враховуючи межу частки похідних\(\dfrac{f′}{g′}\). Важливо усвідомлювати, що ми не обчислюємо похідну від частки\(\dfrac{f}{g}\).

□

Приклад\(\PageIndex{1}\): Applying L’Hôpital’s Rule (0/0 Case)

Оцініть кожне з наступних обмежень, застосовуючи правило L'Hôpital.

\(\displaystyle \lim_{x→0}\dfrac{1−\cos x}{x}\)
\(\displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}\)
\(\displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}\)
\(\displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}\)

Рішення

а Оскільки чисельник\(1−\cos x→0\) та знаменник\(x→0\), ми можемо застосувати правило L'Hôpital для оцінки цієї межі. У нас є

\[\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber \]

b Як\(x→1,\) чисельник\(\sin(πx)→0\) і знаменник\(\ln(x)→0.\) Тому ми можемо застосувати правило L'Hôpital. Отримуємо

\[\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber \]

c. як\(x→∞\), чисельник\(e^{1/x}−1→0\) і знаменник\(\frac{1}{x}→0\). Тому ми можемо застосувати правило L'Hôpital. Отримуємо

\[\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber \]

d Як\(x→0,\) і чисельник, і знаменник наближаються до нуля. Тому ми можемо застосувати правило L'Hôpital. Отримуємо

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber \]

Оскільки чисельник і знаменник цього нового частки обидва наближаються до нуля\(x→0\), ми знову застосовуємо правило L'Hôpital. При цьому ми бачимо, що

\[\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber \]

Тому робимо висновок, що

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber \]

Вправа\(\PageIndex{1}\)

Оцінити\[\lim_{x→0}\dfrac{x}{\tan x}. \nonumber \]

Підказка: \(\dfrac{d}{dx}\big(\tan x\big)=\sec^2x\)

Відповідь: \(1\)

Ми також можемо використовувати правило L'Hôpital для оцінки лімітів коефіцієнтів,\(\dfrac{f(x)}{g(x)}\) в яких\(f(x)→±∞\) і\(g(x)→±∞\). Межі цієї форми класифікуються як невизначені форми типу\(∞/∞\). Знову ж таки, зверніть увагу, що ми насправді не ділимося\(∞\) на\(∞\). Оскільки не\(∞\) є дійсним числом, це неможливо; скоріше,\(∞/∞\) використовується для представлення частки обмежень, кожен з яких є\(∞\) або\(−∞\).

Правило L'Hôpital (\(∞/∞\) Case)

Припустимо\(g\),\(f\) і є диференційованими функціями над відкритим інтервалом\(a\), що містить, крім можливо в\(a\). Припустимо\(\displaystyle\lim_{x→a}f(x)=∞\) (або\(−∞\)) і\(\displaystyle\lim_{x→a}g(x)=∞\) (або\(−∞\)). Потім,

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber \]

припускаючи, що ліміт на право існує або є\(∞\) або\(−∞\). Цей результат також тримається, якщо межа нескінченна\(−∞\), якщо\(a=∞\) або, або межа одностороння.

Приклад\(\PageIndex{2}\): Applying L’Hôpital’s Rule (\(∞/∞\)) Case

Оцініть кожне з наступних обмежень, застосовуючи правило L'Hôpital.

\(\displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}\)
\(\displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}\)

Рішення

а. з тих пір\(3x+5\) and \(2x+1\) are first-degree polynomials with positive leading coefficients, \(\displaystyle\lim_{x→∞}(3x+5)=∞\) and \(\displaystyle\lim_{x→∞}(2x+1)=∞\). Therefore, we apply L’Hôpital’s rule and obtain

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber \]

Зауважте, що цей ліміт також можна обчислити без застосування правила L'Hôpital. Раніше в розділі ми показали, як оцінити таку межу, діливши чисельник і знаменник на найвищу ступінь х в знаменнику. При цьому ми побачили, що

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber \]

Правило L'Hôpital надає нам альтернативні засоби оцінки цього типу ліміту.

б. тут,\(\displaystyle \lim_{x→0^+}\ln x=−∞\) і\(\displaystyle \lim_{x→0^+}\cot x=∞\). Тому ми можемо застосувати правило L'Hôpital та отримати

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber \]

Тепер як\(x→0^+, \csc^2x→∞\). Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \(\csc x\) to write

\[\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber \]

Зараз\(\displaystyle\lim_{x→0^+}\sin^2x=0\) and \(\displaystyle\lim_{x→0^+}-x=0\), so we apply L’Hôpital’s rule again. We find

\[\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber \]

Ми робимо висновок, що

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber \]

Вправа\(\PageIndex{2}\)

Оцінити\[\lim_{x→∞}\dfrac{\ln x}{5x}. \nonumber \]

Підказка: \(\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}\)

Відповідь: \(0\)

Як уже згадувалося, правило L'Hôpital є надзвичайно корисним інструментом для оцінки лімітів. Важливо пам'ятати, однак, що застосовувати правило L'Hôpital до частки\(\dfrac{f(x)}{g(x)}\), it is essential that the limit of \(\dfrac{f(x)}{g(x)}\) be of the form \(\dfrac{0}{0}\) or \(∞/∞\). Consider the following example.

Приклад\(\PageIndex{3}\): When L’Hôpital’s Rule Does Not Apply

Розглянемо\(\displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.\)

Покажіть, що ліміт не можна оцінити, застосовуючи правило L'Hôpital.

Рішення

Оскільки межі чисельника та знаменника не є нульовими і не є обома нескінченними, ми не можемо застосувати правило L'Hôpital. Якщо ми спробуємо це зробити, ми отримаємо

\[\dfrac{d}{dx}(x^2+5)=2x\nonumber \]

\[\dfrac{d}{dx}(3x+4)=3. \nonumber \]

У цей момент ми б помилково прийшли до висновку, що

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber \]

Однак, так як\(\displaystyle \lim_{x→1}(x^2+5)=6\) і у\(\displaystyle \lim_{x→1}(3x+4)=7,\) нас насправді є

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber \]

Можна зробити висновок, що

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber \]

Вправа\(\PageIndex{3}\)

Поясніть, чому ми не можемо застосувати правило L'Hôpital для оцінки\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\). \(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\)Оцініть іншими способами.

Підказка: Визначте межі чисельника і знаменника окремо.

Відповідь: \(\displaystyle\lim_{x→0^+}\cos x=1.\)Тому ми не можемо застосовувати правило L'Hôpital. Межа частки дорівнює\(∞.\)

Інші невизначені форми

Правило L'Hôpital дуже корисно для оцінки лімітів, що включають\(\dfrac{0}{0}\) невизначені форми і\(∞/∞\). Однак ми також можемо використовувати правило L'Hôpital, щоб допомогти оцінити межі, що включають інші невизначені форми, що виникають при оцінці лімітів. Вирази\(0⋅∞, ∞−∞, 1^∞, ∞^0\), і всі\(0^0\) вважаються невизначеною формами. Ці вирази не є дійсними числами. Швидше вони являють собою форми, що виникають при спробі оцінити певні межі. Далі ми розуміємо, чому це невизначені форми, а потім розуміємо, як використовувати правило L'Hôpital в цих випадках. Ключова ідея полягає в тому, що ми повинні переписати невизначені форми таким чином, щоб ми прийшли до невизначеної форми\(\dfrac{0}{0}\) або\(∞/∞\).

Невизначена форма типу 0⋅∞

Припустимо, ми хочемо оцінити\(\displaystyle \lim_{x→a}(f(x)⋅g(x))\), де\(f(x)→0\) і\(g(x)→∞\) (або\(−∞\)) як\(x→a\). Оскільки один термін у добутку наближається до нуля, а інший термін стає довільно великим (за величиною), з твором може статися все що завгодно. Використовуємо позначення\(0⋅∞\) для позначення форми, яка виникає в даній ситуації. Вираз\(0⋅∞\) вважається невизначеною, оскільки ми не можемо визначити без подальшого аналізу точну поведінку продукту\(f(x)g(x)\) як\(x→∞\). Наприклад, нехай\(n\) буде натуральне ціле число і розглянути

\(f(x)=\dfrac{1}{(x^n+1)}\)і\(g(x)=3x^2\).

Як\(x→∞, f(x)→0\) і\(g(x)→∞\). Однак межа станом на\(x→∞\)\(f(x)g(x)=\dfrac{3x^2}{(x^n+1)}\) різниться, залежно від\(n\). Якщо\(n=2\), то\(\displaystyle\lim_{x→∞}f(x)g(x)=3\). Якщо\(n=1\), то\(\displaystyle\lim_{x→∞}f(x)g(x)=∞\). Якщо\(n=3\), то\(\displaystyle\lim_{x→∞}f(x)g(x)=0\). Тут ми розглянемо ще одну межу, що включає невизначену форму\(0⋅∞\) і покажемо, як переписати функцію як частку, щоб використовувати правило L'Hôpital.

Приклад\(\PageIndex{4}\): Indeterminate Form of Type \(0⋅∞\)

Оцінити\(\displaystyle \lim_{x→0^+}x\ln x.\)

Рішення

По-перше, перепишіть функцію\(x\ln x\) як частку, щоб застосувати правило L'Hôpital. Якщо ми пишемо

\[x\ln x=\dfrac{\ln x}{1/x} \nonumber \]

ми бачимо, що\(\ln x→−∞\) як\(x→0^+\) і\(\dfrac{1}{x}→∞\) як\(x→0^+\). Тому ми можемо застосувати правило L'Hôpital та отримати

\[\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber \]

Ми робимо висновок, що

\[\lim_{x→0^+}x\ln x=0. \nonumber \]

Функція y = x ln (x) графічна для значень x ≥ 0. При x = 0 значення функції дорівнює 0. — Малюнок\(\PageIndex{2}\): Пошук\(x=0\) межі at функції\(f(x)=x\ln x.\)

Вправа\(\PageIndex{4}\)

Оцінити\[\lim_{x→0}x\cot x. \nonumber \]

Підказка: Напишіть\(x\cot x=\dfrac{x \cos x}{\sin x}\)

Відповідь: \(1\)

Невизначена форма типу\(∞−∞\)

Інший тип невизначеної форми -\(∞−∞.\) Розглянемо наступний приклад. \(n\)Дозволяти натуральне число і нехай\(f(x)=3x^n\) і\(g(x)=3x^2+5\). Як\(x→∞, f(x)→∞\) і\(g(x)→∞\). Нас цікавить\(\displaystyle\lim_{x→∞}(f(x)−g(x))\). Залежно від того, чи\(f(x)\) ростуть швидше,\(g(x)\) ростуть швидше, або вони ростуть з тією ж швидкістю, як ми бачимо далі, в цій межі може статися все що завгодно. Так як\(f(x)→∞\) і\(g(x)→∞\), пишемо\(∞−∞\) для позначення форми цієї межі. Як і у випадку з іншими нашими невизначеними формами, не\(∞−∞\) має сенсу самостійно, і ми повинні зробити більше аналізу, щоб визначити значення межі. Наприклад, припустимо, що показник n у функції\(f(x)=3x^n\) є\(n=3\), то

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber \]

З іншого боку, якщо\(n=2,\) тоді

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber \]

Однак якщо\(n=1\), то

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber \]

Тому межа не може бути визначена лише розглядом\(∞−∞\). Далі ми бачимо, як переписати вираз, що включає невизначену форму\(∞−∞\) як дріб, щоб застосувати правило L'Hôpital.

Приклад\(\PageIndex{5}\): Indeterminate Form of Type \(∞−∞\)

Оцінити\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right). \nonumber \]

Рішення

Об'єднавши дроби, ми можемо записати функцію як частку. Так як найменш спільний знаменник у\(x^2\tan x,\) нас є

\(\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}\).

Як\(x→0^+\), чисельник\(\tan x−x^2→0\) і знаменник\(x^2\tan x→0.\) Тому ми можемо застосувати правило L'Hôpital. Взявши похідні чисельника і знаменника, маємо

\[\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber \]

Як\(x→0^+\),\((\sec^2x)−2x→1\) і\(x^2\sec^2x+2x\tan x→0\). Оскільки знаменник позитивний, оскільки\(x\) наближається до нуля справа, робимо висновок, що

\[\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber \]

Тому,

\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber \]

Вправа\(\PageIndex{5}\)

Оцінити\(\displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right)\).

Підказка: Перепишіть різницю дробів як одиничний дріб.

Відповідь: 0

Інший тип невизначеної форми, що виникає при оцінці меж, включає експоненти. Вирази\(0^0, ∞^0\), і\(1^∞\) все це невизначені форми. Самі по собі ці вирази безглузді, тому що ми не можемо насправді оцінити ці вирази, як ми б оцінювали вираз, що включає дійсні числа. Швидше, ці вирази представляють форми, що виникають при знаходженні меж. Тепер ми вивчимо, як правило L'Hôpital може бути використано для оцінки лімітів, що включають ці невизначені форми.

Оскільки правило L'Hôpital застосовується до коефіцієнтів, ми використовуємо функцію натурального логарифму та її властивості, щоб зменшити задачу, що оцінює межу за участю експонентів до пов'язаної задачі, що включає межу частки. Наприклад, припустимо, що ми хочемо оцінити,\(\displaystyle \lim_{x→a}f(x)^{g(x)}\) і ми приходимо до невизначеної форми\(∞^0\). (\(0^0\)Невизначені форми і\(1^∞\) можуть бути оброблені аналогічно.) Діємо наступним чином. Нехай

\[y=f(x)^{g(x)}. \nonumber \]

Потім,

\[\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber \]

Тому,

\[\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber \]

Оскільки\(\displaystyle \lim_{x→a}f(x)=∞,\) ми це знаємо\(\displaystyle \lim_{x→a}\ln(f(x))=∞\). Тому\(\displaystyle \lim_{x→a}g(x)\ln(f(x))\) має невизначену форму\(0⋅∞\), і ми можемо використовувати методи, обговорювані раніше, щоб переписати вираз\(g(x)\ln(f(x))\) у формі, щоб ми могли застосувати правило L'Hôpital. Припустимо\(\displaystyle \lim_{x→a}g(x)\ln(f(x))=L\), де\(L\) може бути\(∞\) або\(−∞.\) Тоді

\[\lim_{x→a}[\ln(y)]=L. \nonumber \]

Оскільки функція натурального логарифма є безперервною, робимо висновок, що

\[\ln\left(\lim_{x→a}y\right)=L, \nonumber \]

який дає нам

\[\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber \]

Приклад\(\PageIndex{6}\): Indeterminate Form of Type \(∞^0\)

Оцінити\[\lim_{x→∞}x^{1/x}. \nonumber \]

Рішення

Нехай\(y=x^{1/x}\). Тоді,

\[\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber \]

Нам потрібно оцінити\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x}\). Застосовуючи правило L'Hôpital, ми отримуємо

\[\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber \]

Тому,\(\displaystyle \lim_{x→∞}\ln y=0.\) оскільки функція натурального логарифма є безперервною, робимо висновок, що

\[\ln\left(\lim_{x→∞}y\right)=0, \nonumber \]

що призводить до

\[\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\lim_{x→∞}y\right)}=e^0=1. \nonumber \]

Отже,

\[\lim_{x→∞}x^{1/x}=1. \nonumber \]

Вправа\(\PageIndex{6}\)

Оцінити\[\lim_{x→∞}x^{1/\ln(x)}. \nonumber \]

Підказка: Дозвольте\(y=x^{1/\ln(x)}\) і застосуйте натуральний логарифм до обох сторін рівняння.

Відповідь: \(e\)

Приклад\(\PageIndex{7}\): Indeterminate Form of Type \(0^0\)

Оцінити\[\lim_{x→0^+}x^{\sin x}. \nonumber \]

Рішення

Нехай

\[y=x^{\sin x}. \nonumber \]

Тому,

\[\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber \]

Тепер ми оцінюємо\(\displaystyle\lim_{x→0^+}\sin x\ln x.\) з тих пір\(\displaystyle\lim_{x→0^+}\sin x=0\) і\(\displaystyle\lim_{x→0^+}\ln x=−∞\), у нас є невизначена форма\(0⋅∞\). Щоб застосувати правило L'Hôpital, нам потрібно переписати\(\sin x\ln x\) як дріб. Ми могли б написати

\[\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber \]

або

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber \]

Розглянемо перший варіант. У цьому випадку, застосовуючи правило L'Hôpital, ми отримаємо

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber \]

На жаль, у нас є не тільки інший вираз, що включає невизначену форму,\(0⋅∞,\) але й нову межу оцінити ще складніше, ніж той, з якого ми почали. Замість цього спробуємо другий варіант. Шляхом написання

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber \]

і застосовуючи правило L'Hôpital, ми отримуємо

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber \]

Використовуючи те, що\(\csc x=\dfrac{1}{\sin x}\) і\(\cot x=\dfrac{\cos x}{\sin x}\), ми можемо переписати вираз з правого боку як

\[\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber \]

Ми робимо висновок, що\(\displaystyle\lim_{x→0^+}\ln y=0.\) Отже,\(\displaystyle\ln\left(\lim_{x→0^+}y\right)=0\) і ми маємо

\[\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber \]

Отже,

\[\lim_{x→0^+}x^{\sin x}=1. \nonumber \]

Вправа\(\PageIndex{7}\)

Оцінити\(\displaystyle \lim_{x→0^+}x^x\).

Підказка: Нехай\(y=x^x\) і візьмемо натуральний логарифм обох сторін рівняння.

Відповідь: 1

Темпи зростання функцій

Припустимо, функції\(f\) і\(g\) обидва наближаються до\(x→∞\) нескінченності як Хоча значення обох функцій стають довільно великими, оскільки значення\(x\) стають досить великими, іноді одна функція зростає швидше, ніж інша. Наприклад,\(f(x)=x^2\) і\(g(x)=x^3\) обидва наближаються до нескінченності як\(x→∞\). Однак, як\(\PageIndex{1}\) показує таблиця, значення ростуть\(x^3\) набагато швидше, ніж значення\(x^2\).

Таблиця\(\PageIndex{1}\): Порівняння темпів зростання\(x^2\) і\(x^3\)
\(x\)	10	100	1000	10 000
\(f(x)=x^2\)	100	10 000	1 000 000	100 000 000
\(g(x)=x^3\)	1000	1 000 000	1 000 000 000	1 000 000 000 000

Насправді,

\[\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber \]

або, еквівалентно

\[\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber \]

В результаті, ми говоримо,\(x^3\) зростає швидше, ніж\(x^2\) як\(x→∞\). З іншого боку, для\(f(x)=x^2\) і\(g(x)=3x^2+4x+1\), хоча значення\(g(x)\) завжди більше, ніж значення\(f(x)\) for\(x>0\), кожне значення приблизно втричі перевищує\(g(x)\) відповідне значення\(f(x)\) as\(x→∞\), як показано в табл\(\PageIndex{2}\). Насправді,

\[\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber \]

Таблиця\(\PageIndex{2}\): Порівняння темпів зростання\(x^2\) і\(3x^2+4x+1\)
\(x\)	10	100	1000	10 000
\(f(x)=x^2\)	100	10 000	1 000 000	100 000 000
\(g(x)=3x^2+4x+1\)	341	30 401	3 004 001	300 040 001

При цьому ми говоримо, що\(x^2\) і\(3x^2+4x+1\) ростуть з тією ж швидкістю, що і\(x→∞.\)

Більш загально, припустимо,\(f\) і дві функції, які\(g\) наближаються до нескінченності як\(x→∞\). Ми говоримо,\(g\) зростає швидше, ніж\(f\)\(x→∞\) ніби

\[\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber \]

З іншого боку, якщо існує постійна\(M≠0\) така, що

\[\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber \]

говоримо\(f\) і\(g\) рости з тією ж швидкістю, що і\(x→∞\).

Далі ми бачимо, як використовувати правило L'Hôpital для порівняння темпів зростання потужності, експоненціальних та логарифмічних функцій.

Приклад\(\PageIndex{8}\): Comparing the Growth Rates of \(\ln(x)\), \(x^2\), and \(e^x\)

Для кожної з наступних пар функцій використовуйте правило L'Hôpital для оцінки\[\lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber \]

\(f(x)=x^2\)і\(g(x)=e^x\)
\(f(x)=\ln(x)\)і\(g(x)=x^2\)

Рішення

а. оскільки\(\displaystyle \lim_{x→∞}x^2=∞\) і\(\displaystyle \lim_{x→∞}e^x=∞\), ми можемо використовувати правило L'Hôpital для оцінки\(\displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]\). Отримуємо

\[\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber \]

Оскільки\(\displaystyle \lim_{x→∞}2x=∞\) і\(\displaystyle \lim_{x→∞}e^x=∞\), ми можемо знову застосувати правило L'Hôpital. Так як

\[\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber \]

робимо висновок, що

\[\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber \]

Тому\(e^x\) зростає швидше, ніж\(x^2\) як\(x→∞\) (Див. Малюнок\(\PageIndex{3}\) і Таблицю\(\PageIndex{3}\))

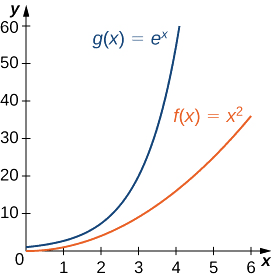
Графічні функції g (x) = ex і f (x) = x2. Очевидно, що g (x) збільшується набагато швидше, ніж f (x). — Малюнок\(\PageIndex{3}\): Експоненціальна функція зростає з більшою швидкістю, ніж силова функція.

Таблиця\(\PageIndex{3}\): Швидкість зростання силової функції та експоненціальної функції.
\(x\)	5	10	15	20
\(x^2\)	25	100	225	400
\(e^x\)	148	22 026	3 269 017	485 165 195

б Оскільки\(\displaystyle \lim_{x→∞}\ln x=∞\) і\(\displaystyle \lim_{x→∞}x^2=∞\), ми можемо використовувати правило L'Hôpital для оцінки\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}\). Отримуємо

\[\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber \]

Таким чином,\(x^2\) зростає швидше, ніж\(\ln x\) як\(x→∞\) (див.\(\PageIndex{4}\) Рис.\(\PageIndex{4}\)

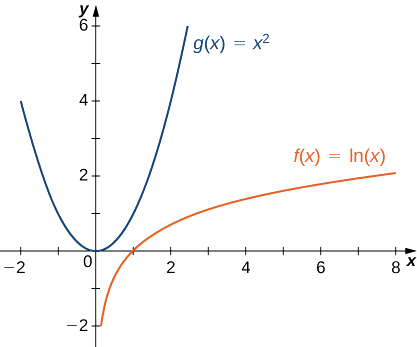
Графічні функції g (x) = x2 і f (x) = ln (x). Очевидно, що g (x) збільшується набагато швидше, ніж f (x). — Малюнок\(\PageIndex{4}\): Функція потужності зростає з більшою швидкістю, ніж логарифмічна функція.

Таблиця\(\PageIndex{4}\): Швидкість зростання степеневої функції та логарифмічної функції
\(x\)	10	100	1000	10 000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(x^2\)	100	10 000	1 000 000	100 000 000

Вправа\(\PageIndex{8}\)

Порівняйте\(x^{100}\) темпи зростання і\(2^x\).

Підказка: Застосувати правило L'Hôpital до\(x^{100}/2^x\).

Відповідь: Функція\(2^x\) зростає швидше, ніж\(x^{100}\).

Використовуючи ті ж ідеї, що і в\(\PageIndex{8}a\) Прикладі. неважко показати, що\(e^x\) росте швидше, ніж\(x^p\) для будь-якої\(p>0\). На малюнку\(\PageIndex{5}\) та таблиці\(\PageIndex{5}\) ми порівнюємо\(e^x\) з\(x^3\) і\(x^4\) як\(x→∞\).

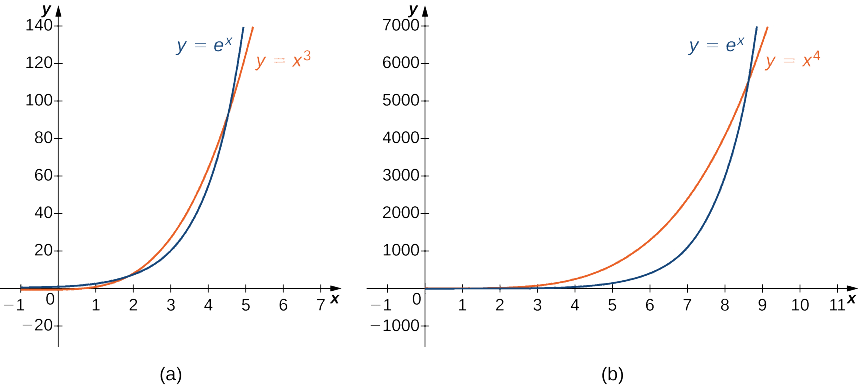
Ця цифра має дві цифри, позначені a і b. на малюнку a позначені функції y = ex і y = x3. Очевидно, що колишній збільшується швидше, ніж х3. На малюнку b позначені графіки функцій y = ex і y = x4. Очевидно, що ex збільшується набагато швидше, ніж x4, але точка, в якій це відбувається, знаходиться далі праворуч, ніж це було для x3. — Малюнок\(\PageIndex{5}\): Експоненціальна функція\(e^x\) зростає швидше, ніж\(x^p\) для будь-якої\(p>0\). (а) Порівняння\(e^x\) з\(x^3\). (б) Порівняння\(e^x\) з\(x^4\).

Таблиця\(\PageIndex{5}\): Експоненціальна функція зростає з більш швидкою швидкістю, ніж будь-яка силова функція
\(x\)	5	10	15	20
\(x^3\)	125	1000	3375	8000
\(x^4\)	625	10 000	50 625	160 000
\(e^x\)	148	22 026	3 269 017	485 165 195

Точно так само нескладно показати, що\(x^p\) росте швидше, ніж\(\ln x\) для будь-якого\(p>0\). На малюнку\(\PageIndex{6}\) і таблиці\(\PageIndex{6}\) ми порівнюємо\(\ln x\) з\(\sqrt[3]{x}\) і\(\sqrt{x}\).

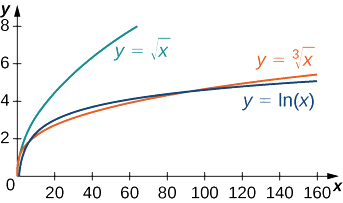
Ця цифра показує y = квадратний корінь x, y = корінь куба x, і y = ln (x). Очевидно, що y = ln (x) зростає повільніше, ніж будь-яка з цих функцій. — Малюнок\(\PageIndex{6}\): Функція\(y=\ln(x)\) зростає повільніше, ніж\(x^p\) для будь-якого\(p>0\) як\(x→∞\).

Таблиця\(\PageIndex{6}\): Логарифмічна функція зростає повільніше, ніж будь-яка коренева функція
\(x\)	10	100	1000	10 000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(\sqrt[3]{x}\)	2.154	4.642	10	21.544
\(\sqrt{x}\)	3.162	10	31.623	100

Ключові концепції

Правило L'Hôpital може бути використано для оцінки межі частки, коли невизначена форма\(\dfrac{0}{0}\) або\(∞/∞\) виникає.
Правило L'Hôpital також може застосовуватися до інших невизначеної форми, якщо вони можуть бути переписані з точки зору межі, що включає частку, яка має невизначену форму\(\dfrac{0}{0}\) або\(∞/∞.\)
Експоненціальна функція\(e^x\) зростає швидше, ніж будь-яка силова функція\(x^p, p>0\).
Логарифмічна функція\(\ln x\) зростає повільніше, ніж будь-яка силова функція\(x^p, p>0\).

Глосарій

невизначені форми: При оцінці ліміту форми\(\dfrac{0}{0}\)\(∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0\), і\(1^∞\) вважаються невизначені, оскільки необхідний подальший аналіз, щоб визначити, чи існує межа і, якщо так, то яке його значення.

Правило L'Hôpital: Якщо\(f\) і\(g\) є диференційованими функціями протягом інтервалу\(a\), крім можливо в\(a\), і\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) або\(\displaystyle \lim_{x→a}f(x)\) і і\(\displaystyle \lim_{x→a}g(x)\) нескінченні, то\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}\), припускаючи, що межа праворуч існує або є\(∞\) або\(−∞\).