4.9: Метод Ньютона
- Page ID
- 62155
- Опишіть кроки методу Ньютона.
- Поясніть, що означає ітераційний процес.
- Розпізнайте, коли метод Ньютона не працює.
- Застосовуйте ітераційні процеси до різних ситуацій.
У багатьох областях чистої та прикладної математики ми зацікавлені в пошуку розв'язків рівняння виду\(f(x)=0.\) Для більшості функцій, однак, важко - якщо не неможливо - обчислити їх нулі явно. У цьому розділі ми розглянемо техніку, яка забезпечує дуже ефективний спосіб наближення нулів функцій. Ця методика використовує наближення дотичних ліній і стоїть за методом, який часто використовується калькуляторами та комп'ютерами для пошуку нулів.
Опис методу Ньютона
Розглянемо завдання знаходження розв'язків\(f(x)=0.\) Якщо\(f\) поліном першого ступеня\(f(x)=ax+b\), то рішення\(f(x)=0\) задається за формулою\(x=−\frac{b}{a}\). Якщо\(f\) поліном другого ступеня\(f(x)=ax^2+bx+c\), то розв'язки\(f(x)=0\) можна знайти за допомогою квадратичної формули. Однак для многочленів 3 ступеня і більше пошук коренів\(f\) стає більш складним. Хоча формули існують для поліномів третього та четвертого ступеня, вони досить складні. Також, якщо f - многочлен ступеня 5 і більше, відомо, що таких формул не існує. Наприклад, розглянемо функцію
\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]
Не існує формули, яка дозволяє знайти розв'язки\(f(x)=0.\) Схожі труднощі існують для неполіноміальних функцій. Для прикладу розглянемо завдання пошуку розв'язків\(\tan(x)−x=0.\) не існує простої формули для розв'язків цього рівняння. У таких випадках ми можемо використовувати метод Ньютона для наближення коренів.
Метод Ньютона використовує наступну ідею для наближення розв'язків\(f(x)=0.\) Шляхом ескізу графіка\(f\), ми можемо оцінити корінь\(f(x)=0\). Назвемо цю оцінку\(x_0\). Потім ми проведемо дотичну лінію до\(f\) at\(x_0\). Якщо\(f′(x_0)≠0\), ця дотична лінія перетинає\(x\) вісь -в якійсь точці\((x_1,0)\). Тепер нехай\(x_1\) буде наступне наближення до фактичного кореня. Як правило,\(x_1\) ближче, ніж\(x_0\) до фактичного кореня. Далі проводимо дотичну лінію до\(f\) at\(x_1\). Якщо\(f′(x_1)≠0\), ця дотична лінія також перетинає\(x\) -вісь, виробляючи ще одне наближення,\(x_2\). Продовжуємо таким чином, виводячи список наближень:\(x_0,\, x_1,\, x_2,\, ….\) Зазвичай числа\(x_0,\, x_1,\, x_2,\, …\) швидко наближаються до фактичного кореня\(x^*\), як показано на наступному малюнку.
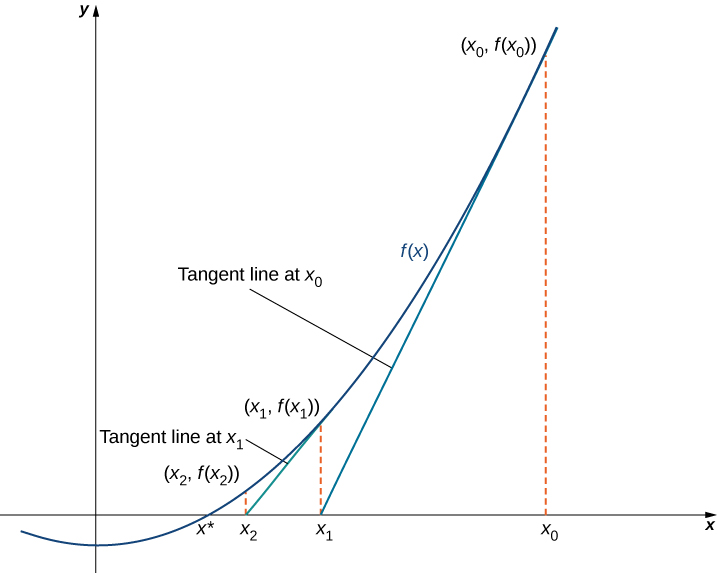
Тепер давайте розглянемо, як обчислити наближення\(x_0,\, x_1,\, x_2,\, ….\) Якщо\(x_0\) наше перше наближення, то наближення\(x_1\) визначається шляхом\((x_1,0)\) дозволу\(x\) -перехоплення дотичної прямої до\(f\) at\(x_0\). Рівняння цієї дотичної прямої задається
\[y=f(x_0)+f′(x_0)(x−x_0). \nonumber \]
Тому\(x_1\) повинні задовольнити
\[f(x_0)+f′(x_0)(x_1−x_0)=0.\nonumber \]
Вирішуючи це рівняння для\(x_1\), зробимо висновок, що
\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}.\nonumber \]
Аналогічно точкою\((x_2,0)\) є\(x\) -перехоплення дотичної лінії до\(f\) at\(x_1\). Тому\(x_2\) задовольняє рівняння
\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}.\nonumber \]
Загалом, для\(n>0,x_n\) задовольняє
\[x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}.\label{Newton} \]
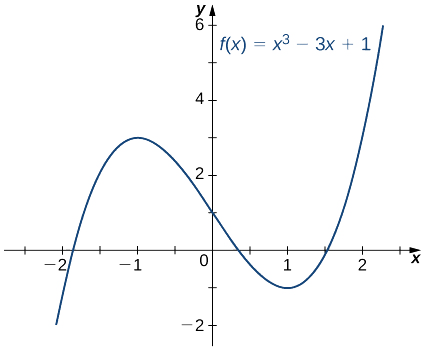
Далі ми бачимо, як використовувати цю техніку для наближення кореня многочлена\(f(x)=x^3−3x+1.\)
Використовуйте метод Ньютона, щоб наблизити корінь\(f(x)=x^3−3x+1\) у інтервалі\([1,2]\). Нехай\(x_0=2\) і знайдуть\(x_1,\, x_2, \,x_3, \,x_4,\) і\(x_5\).
Рішення
З малюнка ми бачимо\(\PageIndex{2}\), що\(f\) має один корінь над інтервалом\([1,2]\). Тому\(x_0=2\) здається розумним першим наближенням. Щоб знайти наступне наближення, ми використовуємо Equation\ ref {Newton}. Так як\(f(x)=x^3−3x+1\), похідна є\(f′(x)=3x^2−3\). Використовуючи Equation\ ref {Newton}\(n=1\) with (і калькулятор, який відображає\(10\) цифри), отримаємо
\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}=2−\frac{f(2)}{f'(2)}=2−\frac{3}{9}≈1.666666667.\nonumber \]
Щоб знайти наступне наближення\(x_2\), ми використовуємо Equation\ ref {Newton} with\(n=2\) і значення,\(x_1\) збережене на калькуляторі. Ми знаходимо, що
\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}≈1.548611111.\nonumber \]
Продовжуючи таким чином, отримуємо наступні результати:
- \(x_1≈1.666666667\)
- \(x_2≈1.548611111\)
- \(x_3≈1.532390162\)
- \(x_4≈1.532088989\)
- \(x_5≈1.532088886\)
- \(x_6≈1.532088886.\)
Відзначимо, що ми отримали однакове значення для\(x_5\) і\(x_6\). Тому будь-яке подальше застосування методу Ньютона, швидше за все, дасть таке ж значення для\(x_n\).
Дозволяючи\(x_0=0\), давайте використовувати метод Ньютона, щоб наблизити корінь\(f(x)=x^3−3x+1\) через інтервал\([0,1]\) шляхом обчислення\(x_1\) і\(x_2\).
- Підказка
-
Використовуйте рівняння\ ref {Ньютон}.
- Відповідь
-
\(x_1≈0.33333333\)
\(x_2≈0.347222222\)
Метод Ньютона також може бути використаний для наближення квадратних коренів. Тут ми покажемо, як наблизити\(\sqrt{2}\). Цей метод можна модифікувати, щоб наблизити квадратний корінь будь-якого додатного числа.
Використовуйте метод Ньютона для наближення\(\sqrt{2}\) (рис.\(\PageIndex{3}\)). Нехай\(f(x)=x^2−2\), нехай\(x_0=2\), і обчислити\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). (Зауважимо, що оскільки\(f(x)=x^2−2\) має нуль при\(\sqrt{2}\), початкове значення\(x_0=2\) є розумним вибором для наближення\(\sqrt{2}\)).
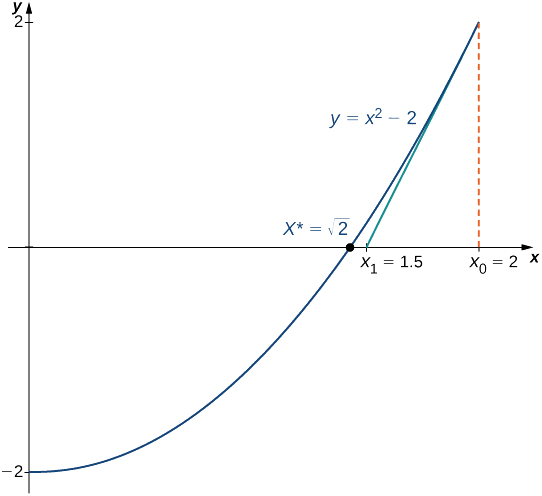
Рішення
Для\(f(x)=x^2−2,\; f′(x)=2x.\) From Equation\ ref {Ньютон}, ми знаємо, що
\ [\ begin {align*} x_n&=x_ {n−1} −\ розрив {f (x_ {n−1})} {f' (x_ {n−1})}\\ [4pt]
&=x_ {n−1}} −\ frac {x^2_ {n−1} −2} {2x_ {n−1}}\ [pt]
&=\ гідророзриву {1} {2} x_ {n−1} +\ гідророзриву {1} {x_ {n−1}}\\ [4pt]
&=\ гідророзриву {1} {2}\ ліворуч (x_ {n−1} +\ frac {2} {x_ {n−1}}\ праворуч). \ end {вирівнювати*}\ nonumber\]
Тому,
\(x_1=\frac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\frac{1}{2}\left(2+\frac{2}{2}\right)=1.5\)
\(x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{1}{2}\left(1.5+\frac{2}{1.5}\right)≈1.416666667.\)
Продовжуючи таким чином, ми виявляємо, що
\(x_1=1.5\)
\(x_2≈1.416666667\)
\(x_3≈1.414215686\)
\(x_4≈1.414213562\)
\(x_5≈1.414213562.\)
Так як ми отримали однакове значення для\(x_4\) і\(x_5\), навряд чи значення\(x_n\) зміниться при будь-якому подальшому застосуванні методу Ньютона. Ми робимо висновок, що\(\sqrt{2}≈1.414213562.\)
Використовуйте метод Ньютона для наближення\(\sqrt{3}\), дозволивши\(f(x)=x^2−3\) і\(x_0=3\). Знайти\(x_1\) і\(x_2\).
- Підказка
-
Для\(f(x)=x^2−3\), Рівняння\ ref {Ньютон} зводиться до\(x_n=\frac{x_{n−1}}{2}+\frac{3}{2x_{n−1}}\).
- Відповідь
-
\(x_1=2\)
\(x_2=1.75\)
При використанні методу Ньютона кожне наближення після початкової здогадки визначається через попереднє наближення за допомогою тієї ж формули. Зокрема, визначаючи функцію\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\), ми можемо переписати Equation\ ref {Newton} як\(x_n=F(x_{n−1})\). Цей тип процесу, де кожен\(x_n\) визначається з\(x_{n−1}\) точки зору повторення однієї і тієї ж функції, є прикладом ітераційного процесу. Коротко ми розглянемо інші ітераційні процеси. Для початку розглянемо причини, за якими методом Ньютона міг не знайти корінь.
Невдачі методу Ньютона
Зазвичай метод Ньютона використовується для пошуку коренів досить швидко. Однак все може піти не так. Деякі причини, чому метод Ньютона може зазнати невдачі, включають наступне:
- При одному з наближень\(x_n\) похідна\(f′\) дорівнює нулю при\(x_n\), але\(f(x_n)≠0\). В результаті дотична лінія\(f\) at\(x_n\) не перетинається з\(x\) -віссю. Тому ми не можемо продовжувати ітераційний процес.
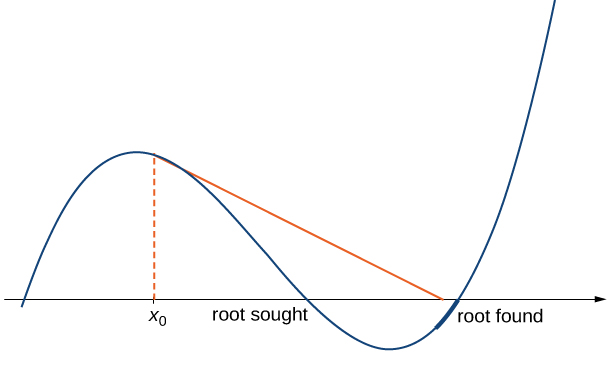
- Наближення\(x_0,\, x_1,\, x_2,\, …\) можуть наближатися до іншого кореня. Якщо функція\(f\) має більше одного кореня, можливо, наші наближення не наближаються до того, за яким ми шукаємо, а наближаються до іншого кореня (див. Рис.\(\PageIndex{4}\)). Ця подія найчастіше відбувається, коли ми не вибираємо наближення досить\(x_0\) близько до потрібного кореня.
- Наближення можуть не наблизитися до кореня повністю. У\(\PageIndex{3}\) прикладі ми наведемо приклад функції та початкову здогадку, що\(x_0\) послідовні наближення ніколи не наближаються до кореня, оскільки послідовні наближення продовжують чергуватися назад і вперед між двома значеннями.
Розглянемо функцію\(f(x)=x^3−2x+2\). Нехай\(x_0=0\). Показати, що послідовність\(x_1,\, x_2,\, …\) не може наблизитися до кореня\(f\).
Рішення
Для\(f(x)=x^3−2x+2,\) похідної\(f′(x)=3x^2−2\) є.Тому,
\[x_1=x_0−\frac{f(x_0)}{f′(x_0)}=0−\frac{f(0)}{f′(0)}=−\frac{2}{−2}=1. \nonumber \]
На наступному кроці,
\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}=1−\frac{f(1)}{f′(1)}=1−\frac{1}{1}=0. \nonumber \]
Отже, числа\(x_0,\, x_1,\, x_2,\, …\) продовжують відскакувати вперед і назад між ними\(0\)\(1\) і ніколи не наближаються до кореня,\(f\) який знаходиться за інтервал\([−2,−1]\) (рис.\(\PageIndex{5}\)). На щастя, якщо ми виберемо початкове наближення\(x_0\) ближче до фактичного кореня, ми зможемо уникнути цієї ситуації.
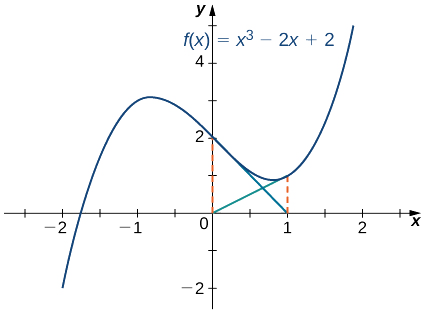
Бо\(f(x)=x^3−2x+2,\) нехай\(x_0=−1.5\) і знайдуть\(x_1\) і\(x_2\).
- Підказка
-
Використовуйте рівняння\ ref {Ньютон}.
- Відповідь
-
\(x_1≈−1.842105263\)
\(x_2≈−1.772826920\)
З Прикладу\(\PageIndex{3}\) ми бачимо, що метод Ньютона не завжди працює. Однак, коли це дійсно працює, послідовність наближень наближається до кореня дуже швидко. Обговорення того, як швидко послідовність наближень наближається до кореня, знайденого методом Ньютона, включено в тексти з чисельного аналізу.
Інші ітераційні процеси
Як уже згадувалося раніше, метод Ньютона є різновидом ітераційного процесу. Тепер ми розглянемо приклад іншого типу ітераційного процесу.
Розглянемо функцію\(F\) і початкове число\(x_0\). Визначте наступні числа\(x_n\) за формулою\(x_n=F(x_{n−1})\). Цей процес є ітераційним процесом, який створює список чисел\(x_0,\, x_1,\, x_2,\, …,\, x_n,\, ….\) Цей список чисел може наблизитися до кінцевого числа,\(x^*\) оскільки\(n\) стає більшим, а може і ні. У прикладі\(\PageIndex{4}\) ми бачимо приклад функції\(F\) і початкове припущення\(x_0\) таке, що результуючий список чисел наближається до кінцевого значення.
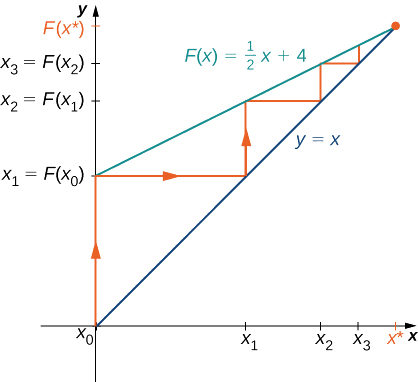
Нехай\(F(x)=\frac{1}{2}x+4\) і нехай\(x_0=0\). Для всіх\(n≥1\) нехай\(x_n=F(x_{n−1})\). Знайдіть значення\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Зробіть здогадки про те, що відбувається з цим списком чисел\(x_1,\, x_2,\, x_3,\, …,\, x_n,\, …\) як\(n→∞\). Якщо список чисел\(x_1,\, x_2,\, x_3,\, …\) наближається до кінцевого числа\(x^*\), то\(x^*\)\(x^*\) задовольняє\(x^*=F(x^*)\), і називається фіксованою точкою\(F\).
Рішення
Якщо\(x_0=0\), то
- \(x_1=\frac{1}{2}(0)+4=4\)
- \(x_2=\frac{1}{2}(4)+4=6\)
- \(x_3=\frac{1}{2}(6)+4=7\)
- \(x_4=\frac{1}{2}(7)+4=7.5\)
- \(x_5=\frac{1}{2}(7.5)+4=7.75\)
- \(x_6=\frac{1}{2}(7.75)+4=7.875\)
- \(x_7=\frac{1}{2}(7.875)+4=7.9375\)
- \(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
- \(x _9=\frac{1}{2}(7.96875)+4=7.984375.\)
З цього списку ми припускаємо, що значення\(x_n\) наближаються\(8\).
Рисунок\(\PageIndex{6}\) містить графічний аргумент, до якого\(8\) наближаються значення\(n→∞\). Починаючи з точки\((x_0,x_0)\), проводимо вертикальну лінію до точки\((x_0,F(x_0))\). Наступний номер в нашому списку -\(x_1=F(x_0)\). Використовуємо\(x_1\) для розрахунку\(x_2\). Тому проводимо горизонтальну лінію, що з'єднується з\((x_0,x_1)\) точкою\((x_1,x_1)\) на лінії\(y=x\), а потім проводимо вертикальну лінію, що\((x_1,x_1)\) з'єднується з точкою\((x_1,F(x_1))\). Виходом\(F(x_1)\) стає\(x_2\). Продовжуючи таким чином, ми могли б створити нескінченну кількість відрізків лінії. Ці відрізки лінії знаходяться в пастці між лініями\(F(x)=\frac{x}{2}+4\) і\(y=x\). Відрізки лінії наближаються до точки перетину цих двох ліній, що відбувається при\(x=F(x)\). Вирішуючи рівняння,\(x=\frac{x}{2}+4,\) робимо висновок, що вони перетинаються в\(x=8\). Тому наші графічні докази погоджуються з нашими чисельними доказами того, що список чисел\(x_0,\, x_1,\, x_2,\, …\) наближається\(x^*=8\) як\(n→∞\).
Розглянемо функцію\(F(x)=\frac{1}{3}x+6\). Нехай\(x_0=0\) і нехай\(x_n=F(x_{n−1})\) для\(n≥2\). Знайти\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Зробіть здогадки про те, що відбувається зі списком чисел\(x_1,\, x_2,\, x_3,\, …\, x_n,\, … \) як\(n→∞.\)
- Підказка
-
Розглянемо точку, де лінії\(y=x\) і\(y=F(x)\) перетинаються.
- Відповідь
-
\(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)
Ітераційні процеси можуть дати дуже цікаву поведінку. У цьому розділі ми бачили кілька прикладів ітераційних процесів, які сходяться до фіксованої точки. Ми також бачили в прикладі\(\PageIndex{3}\), що ітераційний процес відскочив назад і вперед між двома значеннями. Ми називаємо таку поведінку 2-циклом. Ітераційні процеси можуть сходитися до циклів з різною періодичністю, наприклад, 2−циклів, 4-циклів (де ітераційний процес повторює послідовність з чотирьох значень), 8 циклів тощо.
Деякі ітераційні процеси дають те, що математики називають хаосом. У цьому випадку ітераційний процес переходить від значення до значення, здавалося б, випадковим чином і ніколи не сходиться і не осідає в цикл. Хоча повне дослідження хаосу виходить за рамки цього тексту, в цьому проекті ми розглянемо одну з ключових властивостей хаотичного ітераційного процесу: чутливу залежність від початкових умов. Ця властивість відноситься до поняття, що невеликі зміни початкових умов можуть генерувати різко іншу поведінку в ітераційному процесі.
Ймовірно, найвідомішим прикладом хаосу є безліч Мандельброта (див. Рисунок\(\PageIndex{7}\)), названий на честь Бенуа Мандельброта (1924—2010), який досліджував його властивості та допоміг популяризувати область теорії хаосу. Набір Мандельброта зазвичай генерується комп'ютером і показує захоплюючі деталі щодо розширення, включаючи самореплікацію набору. Кілька кольорових версій набору були показані в музеях і їх можна знайти в Інтернеті та в популярних книгах на цю тему.

У цьому проекті ми використовуємо логістичну карту
\[f(x)=rx(1−x) \nonumber \]
де\(x∈[0,1]\) і\(r>0\)
як функція в нашому ітераційному процесі. Логістична карта є оманливо простою функцією; але, залежно від значення\(r\), результуючий ітераційний процес відображає деяку дуже цікаву поведінку. Це може призвести до фіксованих точок, циклів і навіть хаосу.
Для візуалізації довгострокової поведінки ітераційного процесу, пов'язаного з логістичною картою, ми будемо використовувати інструмент під назвою павутинна діаграма. Як ми зробили з ітераційним процесом, який ми розглядали раніше в цьому розділі, спочатку проводимо вертикальну лінію від точки\((x_0,0)\) до точки\((x_0,f(x_0))=(x_0,x_1)\). Потім ми проводимо горизонтальну лінію від цієї точки до точки,\((x_1,x_1),\) потім проведемо вертикальну лінію і продовжуємо процес\((x_1,f(x_1))=(x_1,x_2)\), поки довгострокова поведінка системи не стане очевидною. Малюнок\(\PageIndex{8}\) показує довгострокову поведінку логістичної карти при\(r=3.55\) і\(x_0=0.2\). (Перші\(100\) ітерації не будуються.) Довгострокова поведінка цього ітераційного процесу\(8\) - цикл.
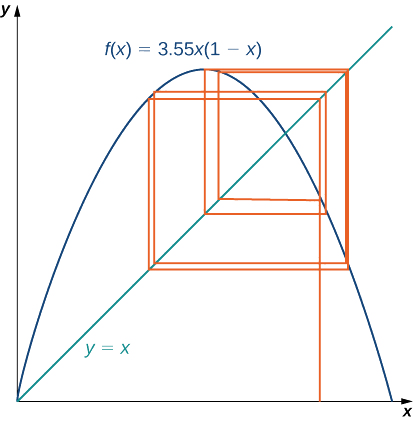
- Нехай\(r=0.5\) і вибирайте\(x_0=0.2\). Або вручну, або за допомогою комп'ютера, обчислити перші\(10\) значення в послідовності. Чи схоже послідовність сходиться? Якщо так, то до якого значення? Це призводить до циклу? Якщо так, то який цикл (наприклад,\(2\) −cycle,\(4\) −cycle.)?
- Що відбувається, коли\(r=2\)?
- Для\(r=3.2\) і\(r=3.5\), обчислити значення першої\(100\) послідовності. Створіть павутинну діаграму для кожного ітераційного процесу. (Кілька безкоштовних аплетів доступні в Інтернеті, які генерують павутинні діаграми для логістичної карти.) Яка довгострокова поведінка в кожному з цих випадків?
- Тепер давайте\(r=4.\) Обчисліть значення першої\(100\) послідовності та створіть павутинну діаграму. Яке довгострокове поведінка в цьому випадку?
- Повторіть процес для\(r=4,\) але нехай\(x_0=0.201.\) Як ця поведінка порівнюється з поведінкою для\(x_0=0.2\)?
Ключові поняття
- Метод Ньютона наближає коріння\(f(x)=0\), починаючи з початкового наближення\(x_0\), потім використовує дотичні лінії до графіка,\(f\) щоб створити послідовність наближень\(x_1,\, x_2,\, x_3,\, ….\)
- Як правило, метод Ньютона є ефективним методом пошуку того чи іншого кореня. У певних випадках метод Ньютона не працює, оскільки список чисел\(x_0,\, x_1,\, x_2,\, …\) не наближається до кінцевого значення або він наближається до значення, відмінного від шуканого кореня.
- Будь-який процес, в якому\(x_0,\, x_1,\, x_2,\, …\) формується список чисел шляхом визначення початкового числа\(x_0\) і визначення наступних чисел за рівнянням\(x_n=F(x_{n−1})\) для якоїсь функції,\(F\) є ітераційним процесом. Метод Ньютона є прикладом ітераційного процесу, де функція\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\) для заданої функції\(f\).
Глосарій
- ітераційний процес
- процес, в якому\(x_0,x_1,x_2,x_3…\) формується список чисел, починаючи з числа\(x_0\) і визначаючи\(x_n=F(x_{n−1})\) для\(n≥1\)
- метод Ньютона
- метод апроксимації коренів з\(f(x)=0;\) використанням початкової здогадки\(x_0\); кожне наступне наближення визначається рівнянням\(x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}\)
