4.4: Теорема про середнє значення

Last updated
Save as PDF

Page ID: 62208

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Поясніть значення теореми Ролля.
Опишіть значення теореми про середнє значення.
Викладіть три важливі наслідки теореми про середнє значення.

Теорема про середнє значення є однією з найважливіших теорем у обчисленні. Ми розглянемо деякі його наслідки в кінці цього розділу. Спочатку почнемо з особливого випадку теореми про середнє значення, яка називається теоремою Ролла.

Теорема Ролла

Неофіційно теорема Ролла стверджує, що якщо виходи диференційовної функції$f$ рівні в кінцевих точках інтервалу, то там повинна бути внутрішня точка,$c$ де$f'(c)=0$. Малюнок$\PageIndex{1}$ ілюструє цю теорему.

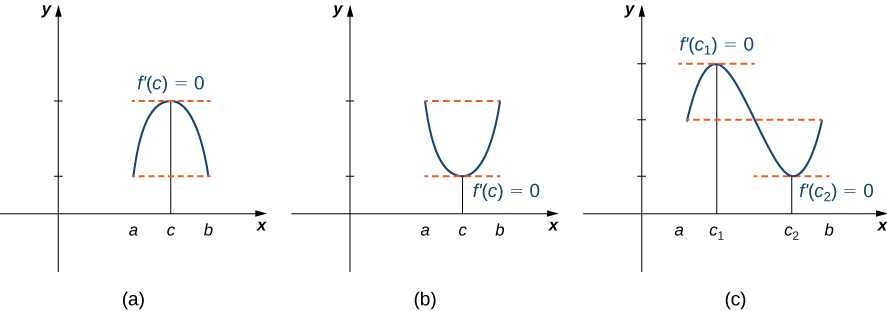
Малюнок розділений на три частини, позначені a, b і c На малюнку a показаний перший квадрант зі значеннями a, c і b, позначені на осі x. Парабола, спрямована вниз, малюється таким чином, що її значення в a і b однакові. Точка c є глобальним максимумом, і зазначається, що f' (c) = 0. На малюнку b показано перший квадрант зі значеннями a, c та b, позначені на осі x. Парабола, звернена вгору, малюється таким чином, що її значення в a і b однакові. Точка c є глобальним мінімумом, і зазначається, що f' (c) = 0. На малюнку c показаний перший квадрант з точками a, c1, c2 та b, позначені на осі x. Один період синусоїди малюється таким чином, щоб його значення при a і b дорівнювали. Точка c1 є глобальним максимумом, і зазначається, що f' (c1) = 0. Точка c2 є глобальним мінімумом, і зазначається, що f' (c2) = 0. — Малюнок$\PageIndex{1}$: Якщо диференційовна функція$f$ задовольняє$f(a)=f(b)$, то її похідна повинна бути нульовою в деякій точці (ах) між$a$ і$b$.

Теорема Ролла

$f$Дозволяти безперервна функція над замкнутим інтервалом$[a,b]$ і диференційована над відкритим інтервалом$(a,b)$ таким чином, що$f(a)=f(b)$. Там тоді існує хоча б один$c∈(a,b)$ такий, що$f'(c)=0.$

Доказ

$k=f(a)=f(b).$Розглянемо три випадки:

$f(x)=k$для всіх$x∈(a,b).$
Існує$x∈(a,b)$ таке, що$f(x)>k.$
Існує$x∈(a,b)$ таке, що$f(x)<k.$

Випадок 1: Якщо$f(x)=k$ для всіх$x∈(a,b)$, то$f'(x)=0$ для всіх$x∈(a,b).$

Випадок 2: Оскільки$f$ є безперервною функцією над замкнутим обмеженим інтервалом$[a,b]$, за теоремою крайніх значень вона має абсолютний максимум. Також, оскільки є$x∈(a,b)$ такий момент$f(x)>k$, що, абсолютний максимум більше$k$. Тому абсолютний максимум не відбувається ні в одній кінцевій точці. В результаті абсолютний максимум повинен відбуватися у внутрішній точці$c∈(a,b)$. Тому що$f$ має максимум у внутрішній точці$c$, і$f$ диференційований$c$, за теоремою Ферма,$f'(c)=0.$

Випадок 3: Випадок, коли існує$x∈(a,b)$ така точка, яка$f(x)<k$ є аналогічною випадку 2, з максимальною заміною на мінімальну.

□

Важливим моментом теореми Ролла є те, що диференційовність функції$f$ є критичною. Якщо$f$ не диференціюється, навіть в одній точці результат може не триматися. Наприклад, функція$f(x)=|x|−1$ є безперервною над$[−1,1]$ і$f(−1)=0=f(1)$, але$f'(c)≠0$ для будь-якої,$c∈(−1,1)$ як показано на наступному малюнку.

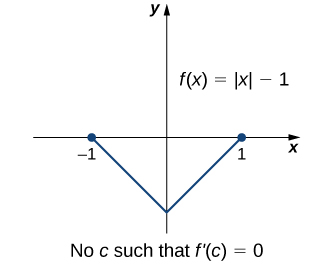
Графічна функція f (x) = |x| − 1. Показано, що f (1) = f (−1), але зазначається, що немає c такого, що f' (c) = 0. — Малюнок$\PageIndex{2}$:$f(x)=|x|−1$ Оскільки не диференційовна при$x=0$, умови теореми Ролла не задовольняються. Насправді висновку тут не тримається; немає$c∈(−1,1)$ такого, що$f'(c)=0.$

Розглянемо тепер функції, що задовольняють умовам теореми Ролла, і обчислимо явно точки,$c$ де$f'(c)=0.$

Приклад$\PageIndex{1}$: Using Rolle’s Theorem

Для кожної з наступних функцій переконайтеся, що функція задовольняє критеріям, зазначеним у теоремі Ролла, і знайти всі значення$c$ в заданому інтервалі, де$f'(c)=0.$

$f(x)=x^2+2x$над$[−2,0]$
$f(x)=x^3−4x$над$[−2,2]$

Рішення

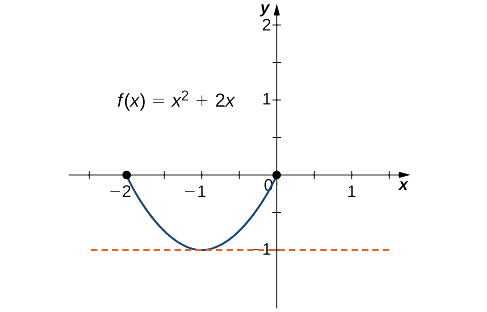
а Оскільки$f$ є многочленом, він є безперервним і диференційованим скрізь. Крім того,$f(−2)=0=f(0).$ Таким чином,$f$ задовольняє критеріям теореми Ролля. Робимо висновок, що існує хоча б одне значення$c∈(−2,0)$ таке, що$f'(c)=0$. Оскільки$f'(x)=2x+2=2(x+1),$ ми бачимо, що це$f'(c)=2(c+1)=0$ означає$c=−1$, як показано на наступному графіку.

Графічна функція f (x) = x2 +2x. Показано, що f (0) = f (−2), а пунктирну горизонтальну лінію проводять за абсолютним мінімумом при (−1, −1). — Рисунок$\PageIndex{3}$: Ця функція є неперервною і диференційованою над [−2,0],$f'(c)=0$ коли$c=−1$.

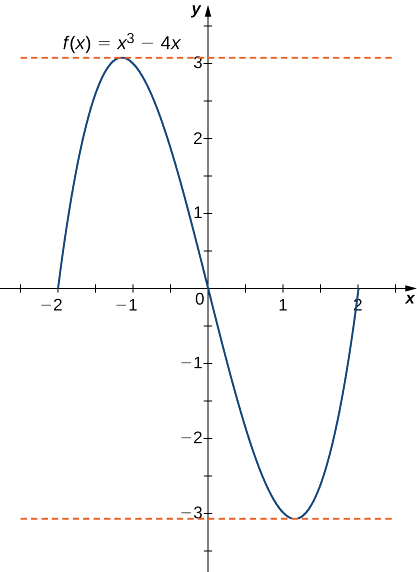
b. як і в частині a.,$f$ є поліномом і тому є безперервним і диференційованим скрізь. Крім$f(−2)=0=f(2).$ того, Це сказав,$f$ задовольняє критеріям теореми Ролла. Диференціюючи, ми знаходимо, що$f'(x)=3x^2−4.$ Тому,$f'(c)=0$ коли$x=±\frac{2}{\sqrt{3}}$. Обидві точки знаходяться в інтервалі$[−2,2]$, і, отже, обидві точки задовольняють висновку теореми Ролла, як показано на наступному графіку.

Графічна функція f (x) = x3 — 4x. Очевидно, що f (2) = f (−2) = f (0). Пунктирні горизонтальні лінії малюються на x = ± 2/квадратний корінь 3, які є локальним максимумом і мінімумом. — Малюнок$\PageIndex{4}$: Для цього многочлена над$[−2,2], f'(c)=0$ at$x=±2/\sqrt{3}$.

Вправа$\PageIndex{1}$

Переконайтеся, що функція,$f(x)=2x^2−8x+6$ визначена за інтервалом,$[1,3]$ задовольняє умовам теореми Ролла. Знайти всі точки,$c$ гарантовані теоремою Ролла.

Підказка: Знайти всі значення$c$, де$f'(c)=0$.

Відповідь: $c=2$

Теорема про середнє значення та її значення

Теорема Ролла є окремим випадком теореми про середнє значення. У теоремі Ролла розглядаються диференційовні функції,$f$ які дорівнюють нулю в кінцевих точках. Теорема про середнє значення узагальнює теорему Ролла, розглядаючи функції, які не обов'язково є нульовими в кінцевих точках. Отже, ми можемо розглядати теорему про середнє значення як похилу версію теореми Ролла (рис.$\PageIndex{5}$). Теорема про середнє значення стверджує,$f$ що якщо безперервна по замкнутому інтервалу$[a,b]$ і диференційована по відкритому інтервалу$(a,b)$, то існує$c∈(a,b)$ така точка, що дотична лінія до графіка$f$ at$c$ паралельна січної лінії, що з'єднує $(a,f(a))$і$(b,f(b)).$

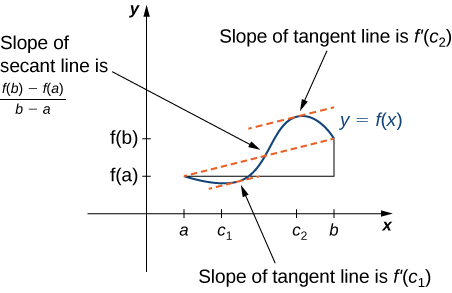
Викреслюється смутно синусоїдальна функція y = f (x). На осі х відзначаються a, c1, c2 і b. На осі у відзначаються f (a) і f (b). Функція f (x) починається з (a, f (a)), зменшується до c1, збільшується до c2, а потім зменшується до (b, f (b)). Між (a, f (a)) і (b, f (b)) проводиться січна лінія, і зазначається, що ця лінія має нахил (f (b) — f (a))/(b − a). Проводяться дотичні лінії при с1 і с2, і ці лінії паралельні січної лінії. Зазначено, що нахили цих дотичних ліній є f' (c1) і f' (c2) відповідно. — Малюнок$\PageIndex{5}$: Теорема про середнє значення говорить, що для функції, яка відповідає її умовам, в якийсь момент дотична лінія має такий же нахил, як і січна лінія між кінцями. Для цієї функції є два значення$c_1$ і$c_2$ такі, що дотична лінія до$f$ at$c_1$ і$c_2$ має такий же нахил, як і січна лінія.

Теорема про середнє значення

$f$Дозволяти бути безперервним за замкнутим інтервалом$[a,b]$ і диференційованим над відкритим інтервалом$(a,b)$. Потім існує хоча б один момент$c∈(a,b)$ такий, що

\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]

Доказ

Доказ випливає з теореми Ролла шляхом введення відповідної функції, яка задовольняє критеріям теореми Ролла. Розглянемо лінію, що з'єднує$(a,f(a))$ і$(b,f(b)).$ Оскільки нахил цієї лінії

\[\frac{f(b)−f(a)}{b−a} \nonumber \]

і лінія проходить через точку$(a,f(a)),$ рівняння цієї лінії можна записати як

\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]

$g(x)$Дозволяти позначити різницю по вертикалі між точкою$(x,f(x))$ і точкою$(x,y)$ на цій лінії. Тому

\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]

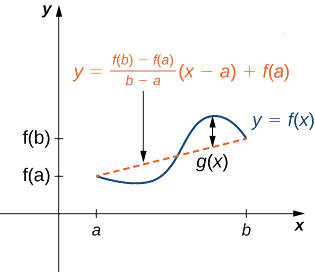$Піднімається, але коливальна крива Y дорівнює F X з січною лінією Y дорівнює F від B мінус F A по всій B мінус A плюс F A, відстань між коливальною кривою і лінією G X$ Малюнок$\PageIndex{6}$: Значення$g(x)$ - це різниця по вертикалі між точкою$(x,f(x))$ і точкою$(x,y)$ на січній лінії, що з'єднує$(a,f(a))$ і$(b,f(b))$.

Оскільки графік$f$ перетинає січну лінію, коли$x=a$ і$x=b$, ми бачимо, що$g(a)=0=g(b)$. Оскільки$f$ є диференційованою функцією над$(a,b)$, також$g$ є диференційованою функцією над$(a,b)$. Крім того,$f$ оскільки безперервний над$[a,b], \, g$ також безперервно закінчується$[a,b]$. Тому$g$ задовольняє критеріям теореми Ролля. Отже, існує$c∈(a,b)$ такий момент, що$g'(c)=0.$ з

\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]

ми бачимо, що

\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]

Оскільки$g'(c)=0,$ ми робимо висновок, що

\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

□

У наступному прикладі ми покажемо, як теорема про середнє значення може бути застосована до функції$f(x)=\sqrt{x}$ через інтервал$[0,9]$. Метод однаковий і для інших функцій, хоча іноді і з більш цікавими наслідками.

Приклад$\PageIndex{2}$: Verifying that the Mean Value Theorem Applies

$f(x)=\sqrt{x}$За проміжком$[0,9]$, показати, що$f$ задовольняє гіпотезу теореми про середнє значення, і тому існує принаймні одне значення$c∈(0,9)$ таке, що$f′(c)$ дорівнює нахилу лінії, що з'єднує$(0,f(0))$ і$(9,f(9))$. Знайдіть ці значення,$c$ гарантовані теоремою про середнє значення.

Рішення

Ми знаємо, що$f(x)=\sqrt{x}$ є безперервним над$[0,9]$ і диференційованим над$(0,9).$ Отже,$f$ задовольняє гіпотези теореми про середнє значення, і має існувати принаймні одне значення$c∈(0,9)$$f′(c)$ таке, яке дорівнює нахилу лінії, що з'єднує$(0,f(0))$ і$(9,f(9))$ (Малюнок$\PageIndex{7}$). Щоб визначити, яке значення (и)$c$ гарантовано, спочатку обчислити похідну від$f$. Похідне$f′(x)=\frac{1}{(2\sqrt{x})}$. Ухил лінії, що$(9,f(9))$ з'єднує$(0,f(0))$ і задається

\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]

Ми хочемо знайти$c$ таке, що$f′(c)=\frac{1}{3}$. Тобто ми хочемо знайти$c$ таке, що

\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]

Вирішуючи це рівняння для$c$, отримаємо$c=\frac{9}{4}$. У цьому місці нахил дотичної лінії дорівнює нахилу лінії, що з'єднує кінцеві точки.

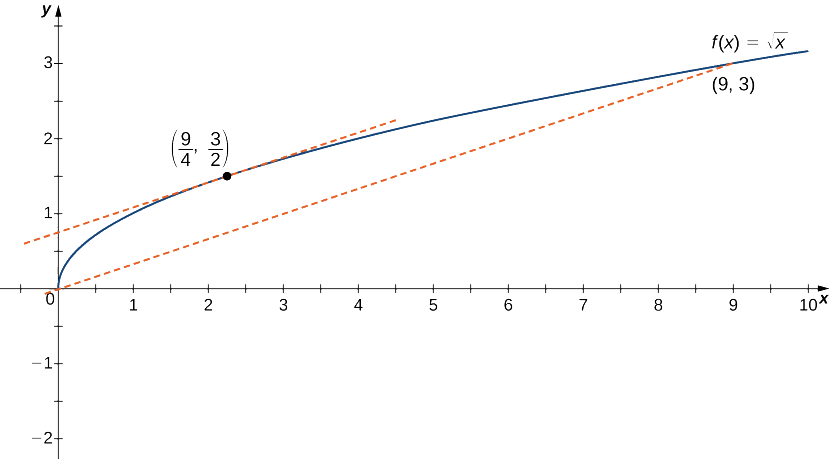
Функція f (x) = квадратний корінь x графується від (0, 0) до (9, 3). Існує січна лінія, проведена від (0, 0) до (9, 3). У точці (9/4, 3/2) є дотична лінія, яка проводиться, і ця лінія паралельна січної лінії. — Малюнок$\PageIndex{7}$: Нахил дотичної лінії в$c=9/4$ такий же, як нахил відрізка лінії, що з'єднує (0,0) і (9,3).

Одна програма, яка допомагає проілюструвати теорему про середнє значення, включає швидкість. Наприклад, припустимо, що ми їдемо на машині протягом 1 години по прямій дорозі із середньою швидкістю 45 км/год. Нехай$s(t)$ і$v(t)$ позначимо положення і швидкість автомобіля, відповідно, для$0≤t≤1$ h. припускаючи,$s(t)$ що функція положення диференційовна, можна застосувати теорему про середнє значення, щоб зробити висновок$c∈(0,1)$, що в якийсь час швидкість автомобіля була точно

\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]

Приклад$\PageIndex{3}$: Mean Value Theorem and Velocity

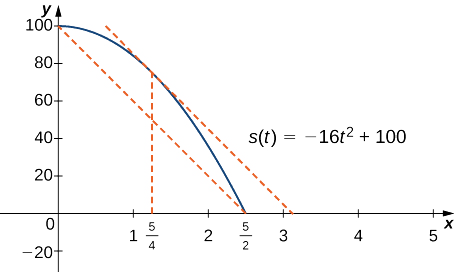
Якщо скеля скидається з висоти 100 футів, її положення$t$ секунд після того, як вона скидається, поки вона не вдариться про землю, задається функцією$s(t)=−16t^2+100.$

Визначте, скільки часу потрібно, перш ніж скеля потрапить на землю.
Знайдіть середню швидкість$v_{avg}$ породи для того, коли скеля звільняється і скеля потрапляє на землю.
Знайти час,$t$ гарантований теоремою про середнє значення, коли миттєва швидкість породи дорівнює$v_{avg}.$

Рішення

а Коли скеля потрапляє на землю, її положення є$s(t)=0$. Вирішуючи рівняння$−16t^2+100=0$ для$t$, знаходимо, що$t=±\frac{5}{2}sec$. Оскільки ми тільки розглядаємо$t≥0$, м'яч потрапить у землю$\frac{5}{2}$ сек після того, як він буде скинутий.

б Середня швидкість задається

\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]

c Миттєва швидкість задається похідною функції положення. Тому нам потрібно знайти$t$ такий час, що$v(t)=s′(t)=v_{avg}=−40$ ft/sec. Оскільки$s(t)$ є безперервним за інтервалом$[0,5/2]$ і диференційованим за інтервалом$(0,5/2),$ за теоремою середнього значення, гарантовано буде$c∈(0,5/2)$ така точка, що

\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]

Беручи похідну функції положення$s(t)$, ми знаходимо, що$s′(t)=−32t.$ Отже, рівняння зводиться до$s′(c)=−32c=−40.$ Розв'язування цього рівняння для$c$, ми маємо$c=\frac{5}{4}$. Отже,$\frac{5}{4}$ сек після скидання породи миттєва швидкість дорівнює середній швидкості породи при її вільному падінні:$−40$ ft/sec.

Функція s (t) = −16t2 + 100 зображена на графіку від (0, 100) до (5/2, 0). Існує січна лінія, проведена від (0, 100) до (5/2, 0). У точці, відповідній х = 5/4, є дотична лінія, яка проводиться, і ця лінія паралельна січної лінії. — Малюнок$\PageIndex{8}$: За час$t=5/4$ сек швидкість породи дорівнює її середній швидкості з моменту її падіння до моменту її удару об землю.

Вправа$\PageIndex{2}$

Припустимо, м'яч скидається з висоти 200 футів. Його положення в часі$t$ -$s(t)=−16t^2+200.$ Знайти час,$t$ коли миттєва швидкість кулі дорівнює його середній швидкості.

Підказка: Для початку визначте, скільки часу потрібно, щоб м'яч потрапив у землю. Потім знайдіть середню швидкість кулі з моменту його падіння, поки він не потрапить на землю.

Відповідь: $\frac{5}{2\sqrt{2}}$сек

Наслідки теореми про середнє значення

Давайте тепер розглянемо три наслідки теореми про середнє значення. Ці результати мають важливі наслідки, які ми використовуємо в наступних розділах.

У цей момент ми знаємо, що похідна будь-якої постійної функції дорівнює нулю. Теорема про середнє значення дозволяє зробити висновок, що зворотне також вірно. Зокрема, якщо$f′(x)=0$ для всіх$x$ в якомусь інтервалі$I$, то$f(x)$ є постійним протягом цього інтервалу. Цей результат може здатися інтуїтивно очевидним, але він має важливі наслідки, які не є очевидними, і ми обговорюємо їх незабаром.

Наслідок 1: Функції з похідною від нуля

$f$Дозволяти диференціюватися протягом інтервалу$I$. Якщо$f′(x)=0$ для всіх$x∈I$, то$f(x)=$ постійний для всіх$x∈I.$

Доказ

Оскільки$f$ диференціюється над$I$,$f$ повинен бути безперервним над$I$. Припустимо$f(x)$, не є постійним для всіх$x$ в$I$. Тоді існують$a,b∈I$, де$a≠b$ і$f(a)≠f(b).$ Виберіть позначення так, щоб$a<b.$ Тому,

\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]

Оскільки$f$ є диференційовною функцією, за теоремою про середнє значення існує$c∈(a,b)$ таке, що

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Тому існує$c∈I$ таке$f′(c)≠0$, що суперечить припущенню, що$f′(x)=0$ для всіх$x∈I$.

□

З «Слідство 1: Функції з похідною нуля» випливає, що якщо дві функції мають однакову похідну, вони відрізняються, максимум, константою.

Наслідок 2: Теорема постійної різниці

Якщо$f$ і$g$ диференційовані по проміжку$I$ і$f′(x)=g′(x)$ для всіх$x∈I$, то$f(x)=g(x)+C$ для якоїсь постійної$C$.

Доказ

Нехай$h(x)=f(x)−g(x).$ тоді,$h′(x)=f′(x)−g′(x)=0$ для всіх$x∈I.$ За наслідком 1, є постійна$C$ така, що$h(x)=C$ для всіх$x∈I$. Тому$f(x)=g(x)+C$ для всіх$x∈I.$

□

Третій наслідок теореми про середнє значення обговорює, коли функція збільшується і коли вона зменшується. Нагадаємо, що функція$f$ збільшується більше,$I$ якщо$f(x_1)<f(x_2)$ щоразу$x_1<x_2$, тоді як$f$ зменшується над$I$ якщо$f(x_1)>f(x_2)$ коли завгодно$x_1<x_2$. Використовуючи теорему про середнє значення, ми можемо показати, що якщо похідна функції позитивна, то функція збільшується; якщо похідна від'ємна, то функція зменшується (рис.$\PageIndex{9}$). Ми використовуємо цей факт у наступному розділі, де ми покажемо, як використовувати похідну функції, щоб знайти локальні максимальні та мінімальні значення функції та як визначити форму графіка.

Цей факт важливий, оскільки це означає, що для даної функції$f$, якщо існує$F$ така функція, що$F′(x)=f(x)$; тоді, єдині інші функції, які мають похідну рівну,$f$ є$F(x)+C$ для деякої константи$C$. Про цей результат ми докладніше обговоримо далі в розділі.

Графікується смутно синусоїдальна функція f (x). Збільшується звідкись у другому квадранті до (a, f (a)). У цьому розділі зазначається, що f' — Рисунок$\PageIndex{9}$: Якщо функція має позитивну похідну протягом деякого інтервалу$I$, то функція збільшується протягом цього інтервалу$I$; якщо похідна є від'ємною протягом деякого інтервалу$I$, то функція зменшується за цей інтервал$I$.

Наслідок 3: Збільшення та зменшення функцій

$f$Дозволяти бути безперервним за замкнутим інтервалом$[a,b]$ і диференційованим над відкритим інтервалом$(a,b)$.

Якщо$f′(x)>0$ для всіх$x∈(a,b)$, то$f$ це зростаюча функція над$[a,b].$
Якщо$f′(x)<0$ для всіх$x∈(a,b)$, то$f$ є спадною функцією над$[a,b].$

Доказ

Доведемо i.; доказ iii. аналогічний. Припустимо$f$, це не зростаюча функція на$I$. Тоді існують$a$ і$b$ в$I$ такому$a<b$, що, але$f(a)≥f(b)$. Оскільки$f$ є диференційовною функцією над$I$, за теоремою про середнє значення існує$c∈(a,b)$ таке, що

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Так як$f(a)≥f(b)$, ми це знаємо$f(b)−f(a)≤0$. Крім того,$a<b$ говорить нам, що$b−a>0.$ Ми робимо висновок, що

\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]

Втім,$f′(x)>0$ для всіх$x∈I$. Це протиріччя, і тому$f$ має бути зростаючою функцією над$I$.

□

Ключові концепції

Якщо$f$ є безперервним над$[a,b]$ і диференційованим над$(a,b)$ і$f(a)=f(b)$, то існує$c∈(a,b)$ такий момент, що$f′(c)=0.$ Це теорема Ролла.
Якщо$f$ є безперервним над$[a,b]$ і$(a,b)$ диференційованим над, то існує$c∈(a,b)$ така точка, що\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] Це Теорема про середнє значення.
Якщо$f'(x)=0$ над інтервалом$I$,$f$ то постійний над$I$.
Якщо дві диференційовні функції$f$ і$g$ задовольняють$f′(x)=g′(x)$ більше$I$, то$f(x)=g(x)+C$ для якоїсь постійної$C$.
Якщо$f′(x)>0$ над інтервалом$I$,$f$ то збільшується більше$I$. Якщо$f′(x)<0$ закінчився$I$,$f$ то зменшується$I$.

Глосарій

теорема про середнє значення: якщо$f$ безперервний над$[a,b]$ і диференційований над$(a,b)$, то існує$c∈(a,b)$ таке, що$f′(c)=\frac{f(b)−f(a)}{b−a}$

теорема Ролла: якщо$f$ безперервний над$[a,b]$ і диференційований над$(a,b)$, а якщо$f(a)=f(b)$, то існує$c∈(a,b)$ таке, що$f′(c)=0$