3.2: Теорема про середнє значення

Last updated
Save as PDF

Page ID: 60705

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми мотивуємо цей розділ наступним питанням: Припустимо, ви виходите з дому та їдете до будинку свого друга в місті за 100 миль, завершуючи поїздку за дві години. У будь-який момент під час поїздки вам обов'язково доведеться їхати 50 миль на годину?

Відповідаючи на це питання, зрозуміло, що середня швидкість за всю поїздку становить 50 миль/год (тобто 100 миль за 2 години), але питання в тому, чи ваша миттєва швидкість коли-небудь рівно 50 миль/год. Простіше кажучи, ваш спідометр коли-небудь читав рівно 50 миль/год?. Відповідь, за деякими дуже розумними припущеннями, є «так».

Давайте тепер розберемося, чому така ситуація полягає в тексті числення, переводячи його в математичні символи.

Спочатку припустимо, що функція$y = f(t)$ дає відстань (в милі), пройдену від вашого будинку в той час$t$ (в годині), де$0\le t\le 2$. Зокрема, це дає$f(0)=0$ і$f(2)=100$. Нахил січної лінії, що з'єднує початкову і кінцеву точки$(0,f(0))$ і$(2,f(2))$ тому

$
\ гідророзриву {\ Дельта f} {\ Дельта т} =\ frac {f (2) -f (0)} {2-0} =\ гідророзриву {100-0} {2} = 50\,\ текст {mph}.
\]

Нахил в будь-якій точці самого графіка задається похідною$f'(t)$. Так, оскільки відповідь на питання вище - «так», це означає, що в якийсь час під час поїздки похідна приймає значення 50 миль/год. Символічно,

$ ф
'(c) =\ frac {f (2) -f (0)} {2-0} = 50
\]

протягом деякого часу$0\le c \le 2.$

Як щодо загалом? Враховуючи будь-яку функцію$y=f(x)$ та діапазон,$a\le x\le b$ чи значення похідної в певній точці між ними$a$ і$b$ повинно відповідати нахилу січної лінії, що з'єднує точки$(a,f(a))$ і$(b,f(b))$? Або еквівалентно, робить рівняння

\[f'(c) = \frac{f(b)-f(a)}{b-a}\]

доведеться провести для деяких$a < c < b$?

Давайте розглянемо дві функції на прикладі.

Приклад$\PageIndex{1}$: Comparing average and instantaneous rates of change

Розглянемо функції

$ $ f_1 (x) =\ гідророзриву {1} {x^2}\ квадратний\ текст {і}\ квад f_2 (x) = |x|\]

з$a=-1$ і$b=1$ як показано на малюнку$\PageIndex{1}$ (а) і (b) відповідно. Обидві функції мають значення 1 в$a$ і$b$. Тому нахил січної лінії, що з'єднує кінцеві точки, є$0$ в кожному конкретному випадку. Але якщо ви подивитеся на графіки кожного, ви можете побачити, що немає точок на будь-якому графіку, де дотичні лінії мають нульовий нахил. Тому ми з'ясували, що немає$c$ в$[-1,1]$ такому, що

$f' (c) =\ фракція {f (1) -f (-1)} {1- (-1)} = 0.\]

$альт$ $альт$

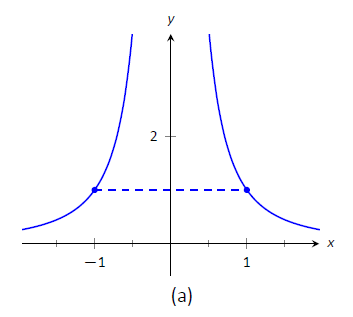
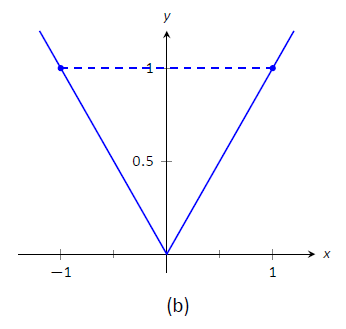
Малюнок$\PageIndex{1}$: Графік$f_1(x) = 1/x^2$ і$f_2(x) = |x|$ в прикладі$\PageIndex{1}$.

Так що ж пішло «неправильно"'? Можливо, не дивно виявити, що розрив$f_1$ і кут$f_2$ відіграють певну роль. Якби наші функції були безперервними та диференційованими, чи змогли б ми знайти це особливе значення$c$? Це наша мотивація до наступної теореми.

Теорема$\PageIndex{1}$: The Mean Value Theorem of Differentiation

$y=f(x)$Дозволяти бути безперервною функцією на замкнутому інтервалі$[a,b]$ і диференційованою на відкритому інтервалі$(a,b)$. Існує таке значення$c$, таке$a < c < b$, що
$$
f' (c) =\ frac {f (b) -f (a)} {b-a}.
$$
Тобто існує значення,$c$ в$(a,b)$ якому миттєва швидкість зміни$f$ at$c$ дорівнює середній швидкості зміни$f$ на$[a,b]$.

Зауважте, що причини того, що функції в Прикладі$\PageIndex{1}$ збій дійсно є те, що$f_1$ має розрив на інтервалі$[-1,1]$ і$f_2$ не диференційований на початку.

Нижче ми наведемо доказ теореми про середнє значення. Для цього ми використовуємо факт, званий теоремою Ролла, викладену тут.

Теорема$\PageIndex{2}$: Rolle's Theorem

$f$Дозволяти бути безперервним$[a,b]$ і диференційованим на$(a,b)$, де$f(a) = f(b)$. Є деякі$c$ в$(a,b)$ такому, що$f'(c) = 0.$

Розглянемо малюнок,$\PageIndex{2}$ де$f$ задано графік функції, де$f(a) = f(b)$. Він повинен мати інтуїтивний сенс,$f$ що якщо диференційований (а отже, і безперервний), що там буде значення$c$,$(a,b)$ де$f'(c)=0$; тобто було б відносний максимум або мінімум$f$ in$(a,b)$. Теорема Ролла гарантує принаймні одну; їх може бути більше.

$альт$

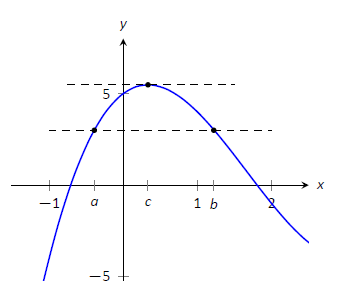
Малюнок$\PageIndex{2}$: Графік$f(x) = x^3-5x^2+3x+5$, де$f(a) = f(b)$. Зверніть увагу на існування$c$, де$a<c<b$, де$f'(c)=0$.

Теорема Ролла насправді є лише окремим випадком теореми про середнє значення. Якщо$f(a) = f(b)$, то середня швидкість зміни на$(a,b)$ є$0$, а теорема гарантує деяке$c$ де$f'(c)=0$. Доведемо теорему Ролла, а потім використаємо її для доведення теореми про середнє значення.

Доказ теореми Ролла

$f$Дозволяти диференціюватися на$(a,b)$ де$f(a)=f(b)$. Розглянемо два випадки.

Випадок 1: Розглянемо випадок, коли$f$ є постійним$[a,b]$; тобто$f(x) = f(a) = f(b)$ для всіх$x$ в$[a,b]$. Тоді$f'(x) = 0$ для всіх$x$ в$[a,b]$, показуючи, що є принаймні одне значення$c$ в$(a,b)$ де$f'(c)=0$.

Випадок 2: Тепер припустимо, що$f$ це не постійна$[a,b]$. Теорема про екстремальні значення гарантує, що$f$ має максимальне та мінімальне значення на$[a,b]$, знайдені або в кінцевих точках, або в критичному значенні в$(a,b)$. Оскільки$f(a)=f(b)$ і не$f$ є постійним, зрозуміло, що максимум і мінімум не можна знайти в кінцевих точках. Припустимо, без втрати спільності, що максимум не$f$ зустрічається в кінцевих точках. Тому є$c$ в$(a,b)$ такому, що$f(c)$ є максимальним значенням$f$. За теоремою 3.1.2,$c$ має бути критичним числом$f$; оскільки$f$ диференційований, ми маємо це$f'(c) = 0$, завершуючи доказ теореми.

$\square$

Тепер ми можемо довести теорему про середнє значення.

Доказ теореми про середнє значення

Визначаємо функцію

$ $ г (х) = ф (х) -\ фракція {ф (б) -ф (а)} {б-а} х.\]

Ми знаємо,$g$ що є$(a,b)$ диференційованим і безперервним$f$,$[a,b]$ оскільки є. Ми можемо показати$g(a)=g(b)$ (насправді простіше показати$g(b)-g(a)=0$, чого вистачає). Потім ми можемо застосувати теорему Ролла, щоб гарантувати існування$c \in (a,b)$ такого, що$g'(c) = 0$. Але зверніть увагу, що

$0= г '(c) = f' (c) -\ frac {f (b) -f (a)} {б-а}\;\]

відтак

$f' (c) =\ гідророзриву {f (b) -f (a)} {б-а},\]

що ми прагнули довести.

$\square$

Повертаючись до самого початку розділу, ми бачимо, що єдине припущення, яке нам знадобиться щодо нашої функції відстані,$f(t)$ - це те, що вона буде безперервною та диференційованою протягом$t$ від 0 до 2 годин (обидва розумні припущення). За теоремою про середнє значення ми гарантуємо час під час поїздки, коли наша миттєва швидкість становить 50 миль/год. Цей факт використовується на практиці. Деякі правоохоронні органи стежать за швидкістю руху, перебуваючи в літаках. Вони не вимірюють швидкість за допомогою радара, а скоріше, синхронізуючи окремі автомобілі, коли вони проходять лінії, намальовані на шосе, відстані яких відомі. Офіцер здатний виміряти середню швидкість автомобіля між намальованими лініями; якщо ця середня швидкість перевищує розміщену швидкість, офіцер запевняється, що водій перевищив обмеження швидкості в певний час.

Зауважте, що теорема про середнє значення є теоремою існування. У ньому зазначено, що особливе значення$c$ існує, але воно не дає жодних вказівок про те, як його знайти. Виявляється, коли нам потрібна теорема про середнє значення, існування - це все, що нам потрібно

Приклад$\PageIndex{2}$: Using the Mean Value Theorem

Розглянемо$f(x) = x^3+5x+5$ далі$[-3,3]$. Знайти$c$ в$[-3,3]$ тому, що задовольняє теоремі середнього значення.

Рішення

Середня швидкість зміни$f$ на$[-3,3]$ становить:

\[\frac{f(3)-f(-3)}{3-(-3)} = \frac{84}{6} = 14.\]

Ми хочемо знайти$c$ таке, що$f'(c) = 14$. Знаходимо$f'(x) = 3x^2+5$. Ставимо це рівним 14 і вирішуємо для$x$.

\[ \begin{align*} f'(x) &= 14 \\ 3x^2 +5 &= 14\\ x^2 &= 3\\ x &= \pm \sqrt{3} \approx \pm 1.732 \end{align*}\]

Ми знайшли 2 значення,$c$ в$[-3,3]$ яких миттєва швидкість зміни дорівнює середній швидкості зміни; Теорема про середнє значення гарантувала принаймні одне. На малюнку$\PageIndex{3}$$f$ зображено пунктирною лінією, що представляє середню швидкість зміни; також$x=\pm \sqrt{3}$ наведені лінії, дотичні до$f$ at. Зверніть увагу, як ці лінії паралельні (тобто мають однаковий нахил), що і пунктирна лінія.

$альт$

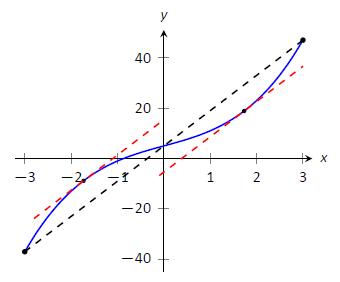
Рисунок$\PageIndex{3}$: Демонстрація теореми про середнє значення на прикладі$\PageIndex{2}$.

Хоча теорема про середнє значення має практичне використання (наприклад, згадане раніше додаток для моніторингу швидкості), вона в основному використовується для просування іншої теорії. Ми будемо використовувати його в наступному розділі, щоб пов'язати форму графіка з його похідною.