3.7: Похідні обернених функцій

Цілі навчання

• Обчислити похідну оберненої функції.
• Розпізнати похідні стандартних обернених тригонометричних функцій.

У цьому розділі ми досліджуємо зв'язок між похідною функції та похідною її оберненої. Для функцій, похідні яких ми вже знаємо, ми можемо використовувати цей зв'язок для пошуку похідних зворотних без необхідності використовувати граничне визначення похідної. Зокрема, ми застосуємо формулу для похідних обернених функцій до тригонометричних функцій. Ця формула також може бути використана для розширення правила влади на раціональні показники.

Похідна оберненої функції

Почнемо з розгляду функції та її зворотного. Якщо$f(x)$ є оборотним і диференційованим, здається розумним, що$f(x)$ зворотне також диференційоване. $\PageIndex{1}$На малюнку показано взаємозв'язок між функцією$f(x)$ та її оберненою$f^{−1}(x)$. Подивіться на точку$\left(a,\,f^{−1}(a)\right)$ на графіку$f^{−1}(x)$ наявності дотичної лінії з нахилом

$$\big(f^{−1}\big)′(a)=\dfrac{p}{q}. \nonumber$$

Ця точка відповідає точці$\left(f^{−1}(a),\,a\right)$ на графіку,$f(x)$ що має дотичну лінію з нахилом

$$f′\big(f^{−1}(a)\big)=\dfrac{q}{p}. \nonumber$$

Таким чином, якщо$f^{−1}(x)$ диференціюється при$a$, то це повинно бути так, що

$\big(f^{−1}\big)′(a)=\dfrac{1}{f′\big(f^{−1}(a)\big)}$.

Малюнок:$\PageIndex{1}$ Дотичні лінії функції та її обернена пов'язані між собою; так само є похідними цих функцій.

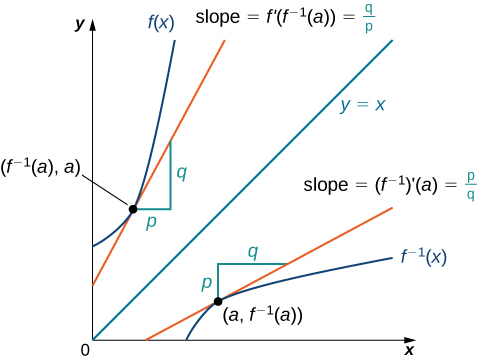
Ми також можемо вивести формулу для похідної від зворотного, спочатку нагадавши про це$x=f\big(f^{−1}(x)\big)$. Потім диференціюючи обидві сторони цього рівняння (використовуючи правило ланцюга праворуч), отримаємо

$1=f′\big(f^{−1}(x)\big)\big(f^{−1}\big)′(x))$.

Вирішуючи для$\big(f^{−1}\big)′(x)$, отримуємо

$\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}$.

Підсумовуємо цей результат в наступній теоремі.

Теорема про обернену функцію

$f(x)$Дозволяти функція, яка є оборотною і диференційованої. $y=f^{−1}(x)$Дозволяти бути зворотним$f(x)$. Для всіх$x$ ситних$f′\big(f^{−1}(x)\big)≠0$,

$$\dfrac{dy}{dx}=\dfrac{d}{dx}\big(f^{−1}(x)\big)=\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}.\label{inverse1}$$

Крім того, якщо$y=g(x)$ є зворотним$f(x)$, то

$$g'(x)=\dfrac{1}{f′\big(g(x)\big)}. \label{inverse2}$$

Приклад$\PageIndex{1}$: Applying the Inverse Function Theorem

Використовуйте теорему оберненої функції, щоб знайти похідну від$g(x)=\dfrac{x+2}{x}$. Порівняйте отриману похідну з отриманою шляхом диференціації функції безпосередньо.

Рішення

$g(x)=\dfrac{x+2}{x}$Зворотне є$f(x)=\dfrac{2}{x−1}$.

Ми будемо використовувати Equation\ ref {inverse2} і почнемо з пошуку$f′(x)$. Таким чином,

$$f′(x)=\dfrac{−2}{(x−1)^2} \nonumber$$

і

$$f′\big(g(x)\big)=\dfrac{−2}{(g(x)−1)^2}=\dfrac{−2}{\left(\dfrac{x+2}{x}−1\right)^2}=−\dfrac{x^2}{2}. \nonumber$$

Нарешті,

$$g′(x)=\dfrac{1}{f′\big(g(x)\big)}=−\dfrac{2}{x^2}. \nonumber$$

Ми можемо переконатися, що це правильна похідна, застосувавши правило частки$g(x)$ до отримання

$$g′(x)=−\dfrac{2}{x^2}. \nonumber$$

Вправа$\PageIndex{1}$

Використовуйте теорему оберненої функції, щоб знайти похідну від$g(x)=\dfrac{1}{x+2}$. Порівняйте отриманий результат шляхом диференціації$g(x)$ безпосередньо.

Підказка

Використовуйте попередній приклад як орієнтир.

Відповідь

$g′(x)=−\dfrac{1}{(x+2)^2}$

Приклад$\PageIndex{2}$: Applying the Inverse Function Theorem

Використовуйте теорему оберненої функції, щоб знайти похідну від$g(x)=\sqrt[3]{x}$.

Рішення

Функція$g(x)=\sqrt[3]{x}$ є оберненою функцією$f(x)=x^3$. З тих пір$g′(x)=\dfrac{1}{f′\big(g(x)\big)}$, почніть з пошуку$f′(x)$. Таким чином,

$$f′(x)=3x^2\nonumber$$

і

$$f′\big(g(x)\big)=3\big(\sqrt[3]{x}\big)^2=3x^{2/3}\nonumber$$

Нарешті,

$$g′(x)=\dfrac{1}{3x^{2/3}}.\nonumber$$

Якби ми диференціювали$g(x)$ безпосередньо, використовуючи правило влади, ми б спочатку переписали$g(x)=\sqrt[3]{x}$ як силу$x$ отримати,

$$g(x) = x^{1/3}\nonumber$$

Тоді ми б диференціювали, використовуючи правило влади для отримання

$$g'(x) =\tfrac{1}{3}x^{−2/3} = \dfrac{1}{3x^{2/3}}.\nonumber$$

Вправа$\PageIndex{2}$

Знайти похідну,$g(x)=\sqrt[5]{x}$ застосувавши обернену теорему функції.

Підказка

$g(x)$є оберненою$f(x)=x^5$.

Відповідь

$g(x)=\frac{1}{5}x^{−4/5}$

З попереднього прикладу ми бачимо, що ми можемо використовувати обернену теорему функції, щоб розширити правило потужності на показники форми$\dfrac{1}{n}$, де$n$ є додатне ціле число. Це розширення в кінцевому підсумку дозволить нам диференціювати$x^q$, де$q$ знаходиться будь-яке раціональне число.

Розширення правила влади на раціональні показники

Правило влади може бути розширено на раціональні показники. Тобто, якщо$n$ є натуральним числом, то

$$\dfrac{d}{dx}\big(x^{1/n}\big)=\dfrac{1}{n} x^{(1/n)−1}. \nonumber$$

Крім того, якщо$n$ є додатним цілим числом і$m$ є довільним цілим числом, то

$$\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}. \nonumber$$

Доказ

Функція$g(x)=x^{1/n}$ є оберненою функцією$f(x)=x^n$. З тих пір$g′(x)=\dfrac{1}{f′\big(g(x)\big)}$, почніть з пошуку$f′(x)$. Таким чином,

$f′(x)=nx^{n−1}$і$f′\big(g(x)\big)=n\big(x^{1/n}\big)^{n−1}=nx^{(n−1)/n}$.

Нарешті,

$g′(x)=\dfrac{1}{nx^{(n−1)/n}}=\dfrac{1}{n}x^{(1−n)/n}=\dfrac{1}{n}x^{(1/n)−1}$.

Щоб диференціювати,$x^{m/n}$ ми повинні переписати його як$(x^{1/n})^m$ і застосувати правило ланцюга. Таким чином,

$$\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{d}{dx}\big((x^{1/n}\big)^m)=m\big(x^{1/n}\big)^{m−1}⋅\dfrac{1}{n}x^{(1/n)−1}=\dfrac{m}{n}x^{(m/n)−1}. \nonumber$$

□

Приклад$\PageIndex{3}$: Applying the Power Rule to a Rational Power

Знайти рівняння прямої дотичної до графіка$y=x^{2/3}$ at$x=8$.

Рішення

Спочатку знайдіть$\dfrac{dy}{dx}$ і оцініть його за адресою$x=8$. Так як

$$\dfrac{dy}{dx}=\frac{2}{3}x^{−1/3} \nonumber$$

і

$$\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber$$

нахил дотичної прямої до графіка при$x=8$ дорівнює$\frac{1}{3}$.

Підставивши$x=8$ в вихідну функцію, отримаємо$y=4$. Таким чином, дотична лінія проходить через точку$(8,4)$. Підставивши в точку-нахил формулу прямої, отримуємо дотичну пряму

$$y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber$$

Вправа$\PageIndex{3}$

Знайдіть похідну від$s(t)=\sqrt{2t+1}$.

Підказка

Скористайтеся правилом ланцюга.

Відповідь

$s′(t)=(2t+1)^{−1/2}$

Похідні обернених тригонометричних функцій

Тепер звернемо увагу на пошук похідних обернених тригонометричних функцій. Ці похідні виявляться неоціненними при вивченні інтеграції пізніше в цьому тексті. Похідні обернених тригонометричних функцій досить дивні тим, що їх похідні насправді є алгебраїчними функціями. Раніше похідні алгебраїчних функцій виявилися алгебраїчними функціями, а похідні тригонометричних функцій були показані як тригонометричні функції. Тут ми вперше бачимо, що похідна функції не повинна бути такого ж типу, як вихідна функція.

Приклад$\PageIndex{4A}$: Derivative of the Inverse Sine Function

Використовуйте теорему оберненої функції, щоб знайти похідну від$g(x)=\sin^{−1}x$.

Рішення

Так як для$x$ в інтервалі$\left[−\frac{π}{2},\frac{π}{2}\right],f(x)=\sin x$ є зворотним$g(x)=\sin^{−1}x$, почніть з знаходження$f′(x)$. Так як

$$f′(x)=\cos x \nonumber$$

і

$$f′\big(g(x)\big)=\cos \big( \sin^{−1}x\big)=\sqrt{1−x^2} \nonumber$$

ми бачимо, що

$$g′(x)=\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{f′\big(g(x)\big)}=\dfrac{1}{\sqrt{1−x^2}} \nonumber$$

Аналіз

Щоб переконатися в$\cos(\sin^{−1}x)=\sqrt{1−x^2}$ цьому, розглянемо наступний аргумент. Набір$\sin^{−1}x=θ$. В даному випадку,$\sin θ=x$ де$−\frac{π}{2}≤θ≤\frac{π}{2}$. Почнемо з розгляду випадку, де$0<θ<\frac{π}{2}$. Оскільки$θ$ це гострий кут, ми можемо побудувати прямокутний трикутник, який має гострий кут$θ$, гіпотенузу довжини$1$ та протилежний бік кута,$θ$ що має довжину$x$. З теореми Піфагора сторона, прилегла до кута,$θ$ має довжину$\sqrt{1−x^2}$. Цей трикутник показаний на малюнку$\PageIndex{2}$ Використовуючи трикутник, ми бачимо, що$\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}$.

Малюнок$\PageIndex{2}$: Використовуючи прямокутний трикутник$θ$, що має гострий кут$1$, гіпотенузу довжини та протилежний бік кута, що$θ$ має довжину$x$, ми бачимо, що$\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}$.

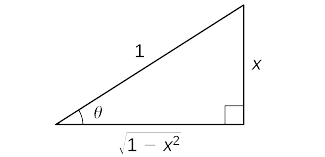
У тому випадку$−\frac{π}{2}<θ<0$, коли, ми робимо спостереження, що$0<−θ<\frac{π}{2}$ і, отже,

$\cos\big(\sin^{−1}x\big)=\cos θ=\cos(−θ)=\sqrt{1−x^2}$.

Тепер, якщо$θ=\frac{π}{2}$ або$θ=−\frac{π}{2},x=1$ або$x=−1$, і так як в будь-якому випадку$\cosθ=0$ і$\sqrt{1−x^2}=0$, у нас є

$\cos\big(\sin^{−1}x\big)=\cosθ=\sqrt{1−x^2}$.

Отже, у всіх випадках

$$\cos\big(\sin^{−1}x\big)=\sqrt{1−x^2}.\nonumber$$

Приклад$\PageIndex{4B}$: Applying the Chain Rule to the Inverse Sine Function

Застосуйте правило ланцюга до формули, отриманої в прикладі,$\PageIndex{4A}$ щоб знайти похідну від$h(x)=\sin^{−1}\big(g(x)\big)$ і використайте цей результат, щоб знайти похідну від$h(x)=\sin^{−1}(2x^3).$

Рішення

Застосовуючи правило ланцюга до$h(x)=\sin^{−1}\big(g(x)\big)$, ми маємо

$h′(x)=\dfrac{1}{\sqrt{1−\big(g(x)\big)^2}}g′(x)$.

Тепер нехай$g(x)=2x^3,$ так$g′(x)=6x^2$. Підставляючи в попередній результат, отримуємо

$\begin{align*} h′(x)&=\dfrac{1}{\sqrt{1−4x^6}}⋅6x^2\\[4pt]&=\dfrac{6x^2}{\sqrt{1−4x^6}}\end{align*}$

Вправа$\PageIndex{4}$

Використовуйте теорему оберненої функції, щоб знайти похідну від$g(x)=\tan^{−1}x$.

Підказка

$g(x)$Зворотне є$f(x)=\tan x$. Використовуйте$\PageIndex{4A}$ Example як орієнтир.

Відповідь

$g′(x)=\dfrac{1}{1+x^2}$

Похідні решти обернених тригонометричних функцій також можна знайти за допомогою теореми обернених функцій. Ці формули наведені в наступній теоремі.

Похідні обернених тригонометричних функцій

$$\begin{align} \dfrac{d}{dx}\big(\sin^{−1}x\big) &=\dfrac{1}{\sqrt{1−x^2}} \label{trig1} \\[4pt] \dfrac{d}{dx}\big(\cos^{−1}x\big) &=\dfrac{−1}{\sqrt{1−x^2}} \label{trig2} \\[4pt] \dfrac{d}{dx}\big(\tan^{−1}x\big) &=\dfrac{1}{1+x^2} \label{trig3} \\[4pt] \dfrac{d}{dx}\big(\cot^{−1}x\big) &=\dfrac{−1}{1+x^2} \label{trig4} \\[4pt] \dfrac{d}{dx}\big(\sec^{−1}x\big) &=\dfrac{1}{|x|\sqrt{x^2−1}} \label{trig5} \\[4pt] \dfrac{d}{dx}\big(\csc^{−1}x\big) &=\dfrac{−1}{|x|\sqrt{x^2−1}} \label{trig6} \end{align}$$

Приклад$\PageIndex{5A}$: Applying Differentiation Formulas to an Inverse Tangent Function

Знайдіть похідну від$f(x)=\tan^{−1}(x^2).$

Рішення

Нехай$g(x)=x^2$, так$g′(x)=2x$. Підставивши в рівняння\ ref {trig3}, отримаємо

$f′(x)=\dfrac{1}{1+(x^2)^2}⋅(2x).$

Спрощуючи, ми маємо

$f′(x)=\dfrac{2x}{1+x^4}$.

Приклад$\PageIndex{5B}$: Applying Differentiation Formulas to an Inverse Sine Function

Знайдіть похідну від$h(x)=x^2 \sin^{−1}x.$

Рішення

Застосовуючи правило продукту, ми маємо

$h′(x)=2x\sin^{−1}x+\dfrac{1}{\sqrt{1−x^2}}⋅x^2$

Вправа$\PageIndex{5}$

Знайдіть похідну від$h(x)=\cos^{−1}(3x−1).$

Підказка

Використовувати рівняння\ ref {trig2}. з$g(x)=3x−1$

Відповідь

$h′(x)=\dfrac{−3}{\sqrt{6x−9x^2}}$

Приклад$\PageIndex{6}$: Applying the Inverse Tangent Function

Положення частинки в часі$t$ задається за допомогою$s(t)=\tan^{−1}\left(\frac{1}{t}\right)$ for$t≥ \ce{1/2}$. Знайти швидкість частинки в часі$t=1$.

Рішення

Почніть з диференціації для$s(t)$ того, щоб знайти$v(t)$ .Таким чином,

$v(t)=s′(t)=\dfrac{1}{1+\left(\frac{1}{t}\right)^2}⋅\dfrac{−1}{t^2}$.

Спрощуючи, ми маємо

$v(t)=−\dfrac{1}{t^2+1}$.

Таким чином,$v(1)=−\dfrac{1}{2}.$

Вправа$\PageIndex{6}$

Знайти рівняння прямої дотичної до графіка$f(x)=\sin^{−1}x$ at$x=0.$

Підказка

$f′(0)$- нахил дотичної лінії.

Відповідь

$y=x$

Ключові поняття

• Теорема оберненої функції дозволяє обчислити похідні обернених функцій без використання граничного визначення похідної.
• Ми можемо використовувати теорему обернених функцій для розробки формул диференціювання обернених тригонометричних функцій.

Ключові рівняння

• Теорема про обернену функцію

$(f^{−1})′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}$всякий раз$f′\big(f^{−1}(x)\big)≠0$ і$f(x)$ диференційований.

• Правило влади з раціональними показниками

$\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}.$

• Похідна оберненої синусоїдальної функції

$\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{\sqrt{1−x^2}}$

• Похідна оберненої косинусної функції

$\dfrac{d}{dx}\big(\cos^{−1}x\big)=\dfrac{−1}{\sqrt{1−x^2}}$

Похідна оберненої тангенсної функції

$\dfrac{d}{dx}\big(\tan^{−1}x\big)=\dfrac{1}{1+x^2}$

Похідна оберненої котангенсної функції

$\dfrac{d}{dx}\big(\cot^{−1}x\big)=\dfrac{−1}{1+x^2}$

Похідна оберненої секантної функції

$\dfrac{d}{dx}\big(\sec^{−1}x\big)=\dfrac{1}{|x|\sqrt{x^2−1}}$

Похідна оберненої косекансної функції

$\dfrac{d}{dx}\big(\csc^{−1}x\big)=\dfrac{−1}{|x|\sqrt{x^2−1}}$

Дописувачі та атрибуція

• Template:ContribOpenStaxCalc
• Paul Seeburger (Monroe Community College) added the second half of Example $\PageIndex{2}$.