3.5: Похідні тригонометричних функцій

Цілі навчання

• Знайти похідні функції синуса і косинуса.
• Знайдіть похідні стандартних тригонометричних функцій.
• Обчисліть похідні вищого порядку синуса і косинуса.

Одним з найважливіших видів руху у фізиці є просте гармонійне рух, яке пов'язане з такими системами, як об'єкт з масою, що коливається на пружині. Простий гармонічний рух можна описати за допомогою синусоїдних або косинусних функцій. У цьому розділі ми розширюємо наші знання про похідні формули, включивши похідні цих та інших тригонометричних функцій. Почнемо з похідних синусоїдних і косинусних функцій і потім використовуємо їх для отримання формул для похідних інших чотирьох тригонометричних функцій. Можливість обчислити похідні синусоїдних і косинусних функцій дозволить нам знайти швидкість і прискорення простого гармонічного руху.

Похідні синусоїдних і косинусних функцій

Розвідку похідної для синусоїдальної функції ми починаємо з використання формули, щоб зробити розумну здогадку на її похідній. Нагадаємо, що для функції$f(x),$

$$f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber$$

Отже, для значень$h$ дуже близьких до$0$,

$$f′(x)≈\dfrac{f(x+h)−f(x)}{h}. \nonumber$$

Ми бачимо, що$h=0.01$, використовуючи,

$$\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber$$

За налаштуванням

$$D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber$$

і за допомогою графічної утиліти ми можемо отримати графік наближення до похідної від$\sin x$ (рис.$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Графік функції дуже$D(x)$ схожий на косинусну криву.

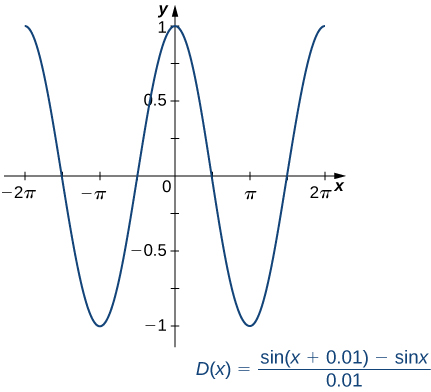
При огляді графік$D(x)$ виявляється дуже близьким до графіка функції косинуса. Дійсно, ми покажемо, що

$$\dfrac{d}{dx}(\sin x)=\cos x. \nonumber$$

Якби ми виконали ті самі кроки, щоб наблизити похідну від функції косинуса, ми б виявили, що

$$\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber$$

Похідні$\sin x$ and $\cos x$

Похідна функції синуса - косинус, а похідна функції косинуса - негативний синус.

$$\dfrac{d}{dx}(\sin x)=\cos x \nonumber$$

$$\dfrac{d}{dx}(\cos x)=−\sin x \nonumber$$

Доказ

Оскільки$\dfrac{d}{dx}(\sin x)=\cos x$ докази та$\dfrac{d}{dx}(\cos x)=−\sin x$ використання подібних методів, ми надаємо лише докази для$\dfrac{d}{dx}(\sin x)=\cos x$. Перед початком згадайте два важливих тригонометричних межі:

$\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1$і$\displaystyle \lim_{h→0}\dfrac{\cos h−1}{h}=0$.

Графіки$y=\dfrac{\sin h}{h}$ і$y=\dfrac{\cos h−1}{h}$ наведені на рис$\PageIndex{2}$.

Рисунок$\PageIndex{2}$: Ці графіки показують дві важливі межі, необхідні для встановлення похідних формул для синусоїдних і косинусних функцій.

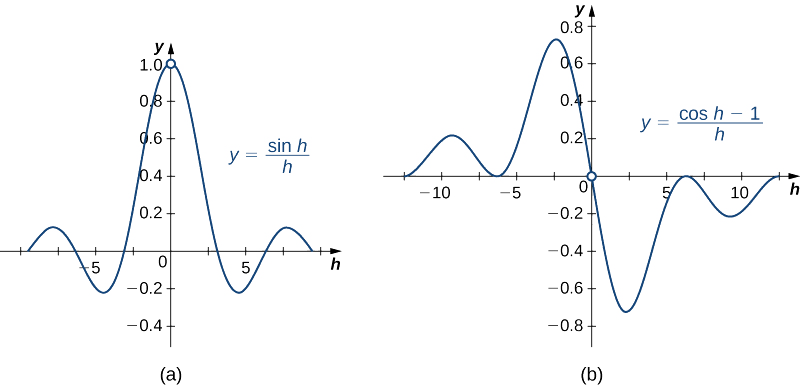
Згадаємо також наступну тригонометричну ідентичність синуса суми двох кутів:

$$\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber$$

Тепер, коли ми зібрали всі необхідні рівняння та тотожності, приступаємо до доказування.

\ [\ begin {align*}\ dfrac {d} {dx} (\ sin x) &=\ lim_ {h→0}\ dfrac {\ sin (x+h) −\ sin x} {h} &\ text {Застосувати визначення похідної.}\\ [4pt]
&=\ lim_ {h→0}\ dfrac {\ sin x\ cos h+\ cos x\ sin h −\ sin x} {h} &\ text {Використовувати ідентичність трига для синуса суми двох кутів.}\\ [4pt]
&=\ lim_ {h → 0}\ ліворуч (\ dfrac {\ sin x\ cos h -\ sin x} {h} +\ dfrac {\ cos x\ sin h} {h}\ праворуч) &\ text {перегрупувати.}\\ [4pt]
&=\ lim_ {h → 0}\ ліворуч (\ sin x\ ліворуч (\ dfrac {\ cos h−1} {h}\ праворуч) + (\ cos x)\ ліворуч (\ dfrac {\ sin h} {h}\ праворуч)\ праворуч) &\ text {Фактор}\ sin x\ text {і}\ cos x\\ [4pt]
& =(\ sin x)\ lim_ {h → 0}\ ліворуч (\ dfrac {\ cos h−1} {h}\ праворуч) + (\ cos x)\ lim_ {h→0}\ ліворуч (\ dfrac {\ sin h} {h}\ праворуч) &\ текст {фактор}\ sin x\ text {і}\ cos x\ текст {з обмеження.}\\ [4pt]
& =(\ sin x) (0) + (\ cos x) (1) &\ text {Застосувати формули обмеження трига.}\\ [4pt]
&=\ cos x & &\ текст {спростити.} \ end {вирівнювати*}\ nonumber\]

□

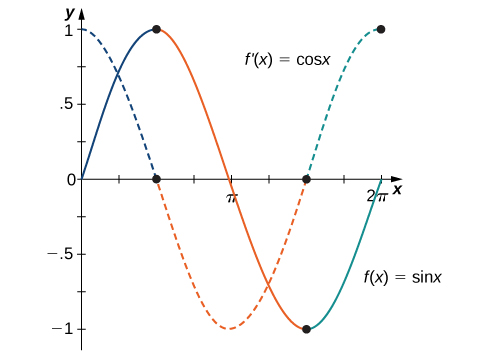
$\PageIndex{3}$На малюнку показана залежність між графіком$f(x)=\sin x$ і його похідною$f′(x)=\cos x$. Зверніть увагу, що в точках, де$f(x)=\sin x$ має горизонтальний тангенс, його похідна$f′(x)=\cos x$ приймає значення нуль. Ми також бачимо, що де f$(x)=\sin x$ збільшується,$f′(x)=\cos x>0$ а де$f(x)=\sin x$ зменшується,$f′(x)=\cos x<0.$

Малюнок$\PageIndex{3}$: Де$f(x)$ має максимум або мінімум,$f'(x)=0$ тобто$f'(x)=0$ де$f(x)$ має горизонтальну дотичну. Ці точки відзначені крапками на графіках

Приклад$\PageIndex{1}$: Differentiating a Function Containing $\sin x$

Знайдіть похідну від$f(x)=5x^3\sin x$.

Рішення

Використовуючи правило продукту, ми маємо

$$\begin{align*} f'(x) &=\dfrac{d}{dx}(5x^3)⋅\sin x+\dfrac{d}{dx}(\sin x)⋅5x^3 \\[4pt] &=15x^2⋅\sin x+\cos x⋅5x^3. \end{align*}$$

Після спрощення отримуємо

$$f′(x)=15x^2\sin x+5x^3\cos x. \nonumber$$

Вправа$\PageIndex{1}$

Знайдіть похідну від$f(x)=\sin x\cos x.$

Підказка

Не забудьте скористатися правилом продукту.

Відповідь

$$f′(x)=\cos^2x−\sin^2x \nonumber$$

Приклад$\PageIndex{2}$: Finding the Derivative of a Function Containing cos x

Знайдіть похідну від$g(x)=\dfrac{\cos x}{4x^2}$.

Рішення

Застосовуючи правило частки, ми маємо

$$g′(x)=\dfrac{(−\sin x)4x^2−8x(\cos x)}{(4x^2)^2}. \nonumber$$

Спрощуючи, отримуємо

$$g′(x)=\dfrac{−4x^2\sin x−8x\cos x}{16x^4}=\dfrac{−x\sin x−2\cos x}{4x^3}. \nonumber$$

Вправа$\PageIndex{2}$

Знайдіть похідну від$f(x)=\dfrac{x}{\cos x}$.

Підказка

Скористайтеся правилом частки.

Відповідь

$f'(x) = \dfrac{\cos x+x\sin x}{\cos^2x}$

Приклад$\PageIndex{3}$: An Application to Velocity

Частка рухається вздовж осі координат таким чином, що її положення в часі$t$ задається$s(t)=2\sin t−t$ for$0≤t≤2π.$ У який час частка знаходиться в стані спокою?

Рішення

Щоб визначити, коли частинка знаходиться в стані спокою, встановлюємо$s′(t)=v(t)=0.$ Почати з знаходження$s′(t).$ Ми отримуємо

$$s′(t)=2 \cos t−1, \nonumber$$

тому ми повинні вирішити

$$2 \cos t−1=0\text{ for }0≤t≤2π. \nonumber$$

Розв'язками цього рівняння є$t=\dfrac{π}{3}$ і$t=\dfrac{5π}{3}$. При цьому частка знаходиться в спокої часом$t=\dfrac{π}{3}$ і$t=\dfrac{5π}{3}$.

Вправа$\PageIndex{3}$

Частка рухається вздовж осі координат. Його положення в часі$t$ задається$s(t)=\sqrt{3}t+2\cos t$ для$0≤t≤2π.$ У який час частка знаходиться в стані спокою?

Підказка

Використовуйте попередній приклад як орієнтир.

Відповідь

$t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}$

Похідні інших тригонометричних функцій

Оскільки решта чотирьох тригонометричних функцій можуть бути виражені у вигляді коефіцієнтів за участю синуса, косинуса або обох, ми можемо використовувати часткове правило для пошуку формул для їх похідних.

Приклад$\PageIndex{4}$: The Derivative of the Tangent Function

Знайдіть похідну від$f(x)=\tan x.$

Рішення

Почніть з вираження$\tan x$ як частка$\sin x$ і$\cos x$:

$f(x)=\tan x =\dfrac{\sin x}{\cos x}$.

Тепер застосуйте часткове правило, щоб отримати

$f′(x)=\dfrac{\cos x\cos x−(−\sin x)\sin x}{(\cos x)^2}$.

Спрощуючи, отримуємо

$$f′(x)=\dfrac{\cos^2x+\sin^2 x}{\cos^2x}. \nonumber$$

$\cos^2x+\sin^2x=1,$Визнаючи, що за теоремою Піфагора, ми тепер маємо

$$f′(x)=\dfrac{1}{\cos^2x} \nonumber$$

Нарешті, використовуйте посвідчення$\sec x=\dfrac{1}{\cos x}$ для отримання

$f′(x)=\text{sec}^2 x$.

Вправа$\PageIndex{4}$

Знайдіть похідну від$f(x)=\cot x .$

Підказка

Перепишіть$\cot x$ як$\dfrac{\cos x}{\sin x}$ і використовуйте часткове правило.

Відповідь

$f′(x)=−\csc^2 x$

Похідні інших тригонометричних функцій можуть бути отримані за допомогою аналогічних прийомів. Ці формули ми наводимо в наступній теоремі.

Похідні$\tan x$, $\cot x$, $\sec x$, and $\csc x$

Похідні інших тригонометричних функцій такі:

\ [\ почати {вирівнювання}\ dfrac {d} {dx} (\ тан х) &=\ сек^2x\\ [4pt]
\ dfrac {d} {dx} (\ кот х) &=−\ csc^2x\\ [4pt]
\ dfrac {d} {dx} (\ сек х) &=\ сек х\ tan x\\ [4pt]
\ dfrac {d} {dx} (\ csc x) &=−\ csc x\ cot x.\ кінець {вирівняти}\ nonumber\]

Приклад$\PageIndex{5}$: Finding the Equation of a Tangent Line

Знайти рівняння прямої дотичної до графіка$f(x)=\cot x$ at$x=\frac{π}{4}$.

Рішення

Щоб знайти рівняння дотичної лінії, нам потрібна точка і нахил в цій точці. Щоб знайти точку, обчисліть

$f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1$.

Таким чином дотична лінія проходить через точку$\left(\frac{π}{4},1\right)$. Далі знайдіть нахил, знайшовши похідну від$f(x)=\cot x$ і оцінивши її за адресою$\frac{π}{4}$:

$f′(x)=−\csc^2 x$і$f′\left(\frac{π}{4}\right)=−\csc^2\left(\frac{π}{4}\right)=−2$.

Використовуючи рівняння точка-нахил прямої, отримаємо

$y−1=−2\left(x−\frac{π}{4}\right)$

або еквівалентно,

$y=−2x+1+\frac{π}{2}$.

Приклад$\PageIndex{6}$: Finding the Derivative of Trigonometric Functions

Знайдіть похідну від$f(x)=\csc x+x\tan x .$

Рішення

Щоб знайти цю похідну, ми повинні використовувати як правило суми, так і правило добутку. Використовуючи правило суми, знаходимо

$f′(x)=\dfrac{d}{dx}(\csc x)+\dfrac{d}{dx}(x\tan x )$.

У першому семестрі,$\dfrac{d}{dx}(\csc x)=−\csc x\cot x ,$ і застосовуючи правило продукту до другого терміну, ми отримуємо

$\dfrac{d}{dx}(x\tan x )=(1)(\tan x )+(\sec^2 x)(x)$.

Тому у нас є

$f′(x)=−\csc x\cot x +\tan x +x\sec^2 x$.

Вправа$\PageIndex{5}$

Знайдіть похідну від$f(x)=2\tan x −3\cot x .$

Підказка

Використовуйте правило для диференціації постійної кратної і правило для диференціації різниці двох функцій.

Відповідь

$f′(x)=2\sec^2 x+3\csc^2 x$

Вправа$\PageIndex{6}$

Знайти нахил прямої дотичної до графіка$f(x)=\tan x$ at$x=\dfrac{π}{6}$.

Підказка

Оцініть похідну при$x=\dfrac{π}{6}$.

Відповідь

$\dfrac{4}{3}$

Похідні для вищого порядку

Похідні вищого порядку$\sin x$ і$\cos x$ слідують повторюваному шаблону. Дотримуючись шаблону, ми можемо знайти будь-яку похідну вищого порядку$\sin x$ і$\cos x.$

Приклад$\PageIndex{7}$: Finding Higher-Order Derivatives of $y=\sin x$

Знайдіть перші чотири похідні$y=\sin x.$

Рішення

Кожен крок в ланцюжку нехитрий:

\ [\ почати {вирівнювати*} y&=\ sin x\\ [4pt]
\ dfrac {dy} {dx} &=\ cos x\\ [4pt]
\ dfrac {d^2y} {dx^2} &=−\ sin x\\ [4pt]\ dfrac {d^3y} {dx^3} &= −
\ cos x\\ [4pt]\ dfrac {d^3y} &=\ cos x
\\ 4pt]\ dfrac {d^4y} {dx^4} &=\ sin x\ end {вирівнювати*}\]

Аналіз

Як тільки ми визнаємо закономірність похідних, ми можемо знайти будь-яку похідну вищого порядку, визначивши крок у шаблоні, якому вона відповідає. Наприклад, кожна четверта похідна$\sin x$ дорівнює$\sin x$, так

$$\dfrac{d^4}{dx^4}(\sin x)=\dfrac{d^8}{dx^8}(\sin x)=\dfrac{d^{12}}{dx^{12}}(\sin x)=…=\dfrac{d^{4n}}{dx^{4n}}(\sin x)=\sin x \nonumber$$

$$\dfrac{d^5}{dx^5}(\sin x)=\dfrac{d^9}{dx^9}(\sin x)=\dfrac{d^{13}}{dx^{13}}(\sin x)=…=\dfrac{d^{4n+1}}{dx^{4n+1}}(\sin x)=\cos x. \nonumber$$

Вправа$\PageIndex{7}$

Для$y=\cos x$, знайдіть$\dfrac{d^4y}{dx^4}$.

Підказка

Дивіться попередній приклад.

Відповідь

$\cos x$

Приклад$\PageIndex{8}$: Using the Pattern for Higher-Order Derivatives of $y=\sin x$

Знайти$\dfrac{d^{74}}{dx^{74}}(\sin x)$.

Рішення

Ми відразу бачимо, що для 74-ї похідної$\sin x$$74=4(18)+2$, так

$$\dfrac{d^{74}}{dx^{74}}(\sin x)=\dfrac{d^{72+2}}{dx^{72+2}}(\sin x)=\dfrac{d^2}{dx^2}(\sin x)=−\sin x. \nonumber$$

Вправа$\PageIndex{8}$

Для$y=\sin x$, знайдіть$\dfrac{d^{59}}{dx^{59}}(\sin x).$

Підказка

$\dfrac{d^{59}}{dx^{59}}(\sin x)=\dfrac{d^{4⋅14+3}}{dx^{4⋅14+3}}(\sin x)$

Відповідь

$−\cos x$

Приклад$\PageIndex{9}$: An Application to Acceleration

Частка рухається вздовж осі координат таким чином, що її положення в часі$t$ задається$s(t)=2−\sin t$. Знайти$v(π/4)$ і$a(π/4)$. Порівняйте ці значення і вирішіть, прискорюється чи сповільнюється частка.

Рішення

Перша знахідка$v(t)=s′(t)$

$$v(t)=s′(t)=−\cos t . \nonumber$$

Таким чином,

$v\left(\frac{π}{4}\right)=−\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}$.

Далі знайдіть$a(t)=v′(t)$. Таким чином,$a(t)=v′(t)=\sin t$ і у нас є

$a\left(\frac{π}{4}\right)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$.

Оскільки$v\left(\frac{π}{4}\right)=−\dfrac{\sqrt{2}}{2}<0$ і$a\left(\frac{π}{4}\right)=\dfrac{\sqrt{2}}{2}>0$, ми бачимо, що швидкість і прискорення діють в протилежних напрямках; тобто об'єкт прискорюється в напрямку, протилежному напрямку, в якому він рухається. Отже, частка сповільнюється.

Вправа$\PageIndex{9}$

Блок, прикріплений до пружини, рухається вертикально. Своє становище в момент t задано$s(t)=2\sin t$. Знайти$v\left(\frac{5π}{6}\right)$ і$a\left(\frac{5π}{6}\right)$. Порівняйте ці значення і вирішіть, прискорюється або сповільнюється блок.

Підказка

Використовуйте$\PageIndex{9}$ Example як орієнтир.

Відповідь

$v\left(\frac{5π}{6}\right)=−\sqrt{3}<0$і$a\left(\frac{5π}{6}\right)=−1<0$. Блок прискорюється.

Ключові поняття

• Ми можемо знайти похідні від$\sin x$ і за$\cos x$ допомогою визначення похідних і граничних формул, знайдених раніше. Результати:

$\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big)=−\sin x$.

• За допомогою цих двох формул ми можемо визначити похідні всіх шести основних тригонометричних функцій.

Ключові рівняння

• Похідна синусоїдальної функції

$\dfrac{d}{dx}(\sin x)=\cos x$

• Похідна функції косинуса

$\dfrac{d}{dx}(\cos x)=−\sin x$

• Похідна від тангенсної функції

$\dfrac{d}{dx}(\tan x )=\sec^2x$

• Похідна функції котангенса

$\dfrac{d}{dx}(\cot x )=−\csc^2x$

• Похідна від сікантної функції

$\dfrac{d}{dx}(\sec x)=\sec x\tan x$

• Похідна від косекансної функції

$\dfrac{d}{dx}(\csc x)=−\csc x\cot x$