3.9: Похідні експоненціальних та логарифмічних функцій
- Page ID
- 62229
- Знайти похідну від експоненціальних функцій.
- Знайти похідну логарифмічних функцій.
- Використовуйте логарифмічну диференціацію для визначення похідної функції.
Поки що ми навчилися диференціювати різноманітні функції, включаючи тригонометричні, обернені та неявні функції. У цьому розділі ми досліджуємо похідні експоненціальних та логарифмічних функцій. Як ми обговорювали у Вступ до функцій та графіків, експоненціальні функції відіграють важливу роль у моделюванні зростання населення та розпаду радіоактивних матеріалів. Логарифмічні функції можуть допомогти масштабувати великі величини і особливо корисні для переписування складних виразів.
Похідна від експоненціальної функції
Так само, як коли ми знайшли похідні інших функцій, ми можемо знайти похідні експоненціальних та логарифмічних функцій за допомогою формул. У міру розробки цих формул нам потрібно робити певні основні припущення. Докази, які дотримуються ці припущення, виходять за рамки цього курсу.
Перш за все, почнемо з припущення, що функція\(B(x)=b^x,\, b>0,\) визначена для кожного дійсного числа і є безперервною. У попередніх курсах були визначені значення експоненціальних функцій для всіх раціональних чисел - починаючи з визначення\(b^n\), де\(n\) є додатне ціле число - як добутку\(b\) помноженого на себе\(n\) часу. Пізніше, ми визначили\(b^0=1,b^{−n}=\dfrac{1}{b^n}\), для натурального цілого\(n\), і\(b^{s/t}=(\sqrt[t]{b})^s\) для натуральних чисел\(s\) і\(t\). Ці визначення залишають відкритим питання про значення\(b^r\) де\(r\) - довільне дійсне число. Припускаючи безперервність\(B(x)=b^x,b>0\), ми можемо інтерпретувати\(b^r\),\(\displaystyle \lim_{x→r}b^x\) де значення,\(x\) як ми приймаємо межу, є раціональними. Наприклад, ми можемо розглядати\(4^π\) як число задовольняє
\[4^3<4^π<4^4,\quad 4^{3.1}<4^π<4^{3.2},\quad 4^{3.14}<4^π<4^{3.15}, \nonumber \]
\[4^{3.141}<4^{π}<4^{3.142},\quad 4^{3.1415}<4^{π}<4^{3.1416},\quad …. \nonumber \]
Як ми бачимо в наступній таблиці,\(4^π≈77.88.\)
| \(x\) | \(4^x\) | \(x\) | \(4^x\) |
|---|---|---|---|
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^3\) | \ (4^x\)» style="вирівнювання тексту: центр; "> 64 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.141593}\) | \ (4^x\)» стиль = «вирівнювання тексту: центр;" > 77.8802710486 |
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.1}\) | \ (4^x\)» стиль = «вирівнювання тексту: центр;" > 73.5166947198 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.1416}\) | \ (4^x\)» стиль = «вирівнювання тексту: центр;" > 77.8810268071 |
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.14}\) | \ (4^x\)» стиль = «вирівнювання тексту: центр;" > 77.7084726013 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.142}\) | \ (4^x\)» style="вирівнювання тексту: центр; "> 77.9242251944 |
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.141}\) | \ (4^x\)» style="вирівнювання тексту: центр; "> 77.8162741237 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.15}\) | \ (4^x\)» style="вирівнювання тексту: центр; "> 78.7932424541 |
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.1415}\) | \ (4 ^ x\)» стиль = «вирівнювання тексту: центр;" > 77.8702309526 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.2}\) | \ (4 ^ x\)» стиль = «вирівнювання тексту: центр;" > 84.4485062895 |
| \ (x\)» style="вирівнювання тексту: центр; ">\(4^{3.14159}\) | \ (4^x\)» стиль = «вирівнювання тексту: центр;" > 77.8799471543 | \ (x\)» style="вирівнювання тексту: центр; ">\(4^{4}\) | \ (4^x\)» style="вирівнювання тексту: центр; "> 256 |
Наближення значення\(4^π\)
Також припустимо\(B(x)=b^x,\, b>0\), що для,\(B′(0)\) значення похідної існує. У цьому розділі ми показуємо, що, зробивши це одне додаткове припущення, можна довести, що функція\(B(x)\) є диференційованою скрізь.
Зробимо одне остаточне припущення: що існує унікальне значення\(b>0\) для якого\(B′(0)=1\). Ми визначаємо e як це унікальне значення, як ми це робили у Вступ до функцій та графіків. На малюнку\(\PageIndex{1}\) наведені графіки функцій\(y=2^x, \,y=3^x, \,y=2.7^x,\) і\(y=2.8^x\). Наочна оцінка нахилів дотичних ліній до цих функцій при 0 дає докази того, що значення e лежить десь між 2,7 і 2,8. Функція\(E(x)=e^x\) називається природною експоненціальною функцією. Його обернена,\(L(x)=\log_e x=\ln x\) називається природною логарифмічною функцією.
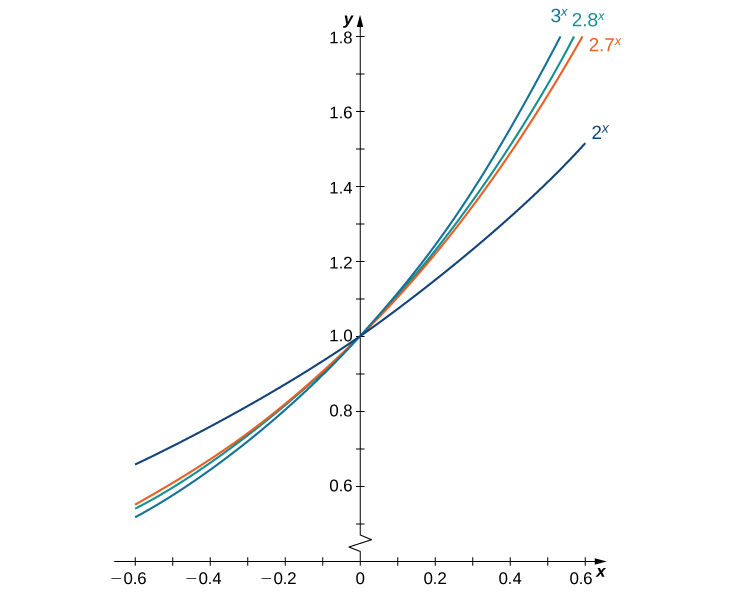
Для кращої оцінки\(e\) ми можемо побудувати таблицю оцінок\(B′(0)\) для функцій виду\(B(x)=b^x\). Перш ніж робити це, нагадайте, що
\[B′(0)=\lim_{x→0}\frac{b^x−b^0}{x−0}=\lim_{x→0}\frac{b^x−1}{x}≈\frac{b^x−1}{x} \nonumber \]
для значень\(x\) дуже близьких до нуля. За нашими оцінками ми вибираємо\(x=0.00001\) і\(x=−0.00001\)
для отримання кошторису
\[\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}. \nonumber \]
Дивіться наступну таблицю.
| \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) | \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) |
|---|---|---|---|
| \ (b\)» style="вирівнювання тексту: центр; "> 2 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(0.693145<B′(0)<0.69315\) | \ (b\)» style="вирівнювання тексту: центр; "> 2.7183 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(1.000002<B′(0)<1.000012\) |
| \ (b\)» style="вирівнювання тексту: центр; "> 2.7 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(0.993247<B′(0)<0.993257\) | \ (b\)» style="вирівнювання тексту: центр; "> 2.719 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(1.000259<B′(0)<1.000269\) |
| \ (b\)» style="вирівнювання тексту: центр; "> 2.71 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(0.996944<B′(0)<0.996954\) | \ (b\)» style="вирівнювання тексту: центр; "> 2.72 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(1.000627<B′(0)<1.000637\) |
| \ (b\)» style="вирівнювання тексту: центр; "> 2.718 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(0.999891<B′(0)<0.999901\) | \ (b\)» style="вирівнювання тексту: центр; "> 2.8 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(1.029614<B′(0)<1.029625\) |
| \ (b\)» style="вирівнювання тексту: центр; "> 2.7182 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(0.999965<B′(0)<0.999975\) | \ (b\)» style="вирівнювання тексту: центр; "> 3 | \ (\ розрив {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)» style="text-align:center; ">\(1.098606<B′(0)<1.098618\) |
Докази з таблиці свідчать про те, що\(2.7182<e<2.7183.\)
Графік\(E(x)=e^x\) разом з лінією\(y=x+1\) наведено на малюнку\(\PageIndex{2}\). Ця лінія є дотичною до графіка\(E(x)=e^x\) at\(x=0\).
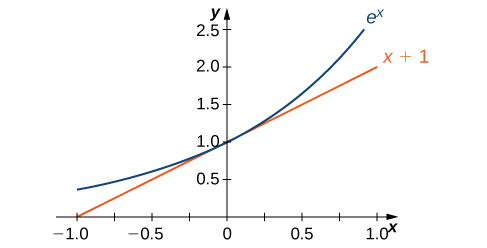
Тепер, коли ми виклали наші основні припущення, ми починаємо наше розслідування з вивчення похідної\(B(x)=b^x, \,b>0\). Нагадаємо, що ми припустили, що\(B′(0)\) існує. Застосовуючи визначення межі до похідної, ми робимо висновок, що
\[B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h} \nonumber \]
\(B′(x)\)Перейшовши до, отримуємо наступне.
\ (\ displaystyle\ begin {align*} B′ (x) &=\ lim_ {h→0}\ frac {b^ {x+h} −b^x} {h} &\ text {Застосувати граничне визначення похідної.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {b^xb^h} &\ текст {Зауважте, що} b^ {x+h} =b^xb^h.\\ [4pt]
&=\ lim_ {h→0}\ frac {b^x (b^h−1)} {h} &\ текст {Фактор з} b^x.\\ [4pt]
&=b^x\ lim_ {h→0}\ frac {b^h−1} {h} &\ text {Застосувати властивість обмежень.}\\ [4pt]
&=B^xB′ (0) &\ текст {Використання} B′ (0) =\ lim_ {h → 0}\ frac b^ {0+h} −b^0} {h} =\ lim_ {h→0}\ frac {b^h−1} {h}. \ end {вирівнювати*}\)
Ми бачимо, що на підставі припущення, яке\(B(x)=b^x\) диференційоване при\(0,B(x)\), не тільки всюди диференціюється, але і його похідна
\[B′(x)=b^xB′(0).\nonumber \]
Для\(E(x)=e^x, \,E′(0)=1.\) Таким чином, ми маємо\(E′(x)=e^x\). (Значення\(B′(0)\) для довільної функції форми\(B(x)=b^x, \,b>0,\) буде виведено пізніше.)
\(E(x)=e^x\)Дозволяти природна експоненціальна функція. Тоді
\[E′(x)=e^x. \nonumber \]
Загалом,
\[\frac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x) \nonumber \]
Знайдіть похідну від\(f(x)=e^{\tan(2x)}\).
Рішення:
Використовуючи похідну формулу і правило ланцюга,
\[f′(x)=e^{\tan(2x)}\frac{d}{dx}\Big(\tan(2x)\Big)=e^{\tan(2x)}\sec^2(2x)⋅2 \nonumber \]
Знайдіть похідну від\(y=\dfrac{e^{x^2}}{x}\).
Рішення
Використовуйте похідну природної експоненціальної функції, часткове правило та правило ланцюга.
\ (\ begin {align*} y′&=\ dfrac {(e^ {x^2} ⋅2) x⋅x−1⋅e^ {x^2}} {x^2} &\ text {Застосувати правило частки.}\\ [4pt]
&=\ dfrac {e^ {x^2} (2x^2−1)} {x^2}} {x^2}} &\ текст {Спрощення.} \ end {вирівнювати*}\)
Знайдіть похідну від\(h(x)=xe^{2x}\).
- Підказка
-
Не забудьте скористатися правилом продукту.
- Відповідь
-
\(h′(x)=e^{2x}+2xe^{2x}\)
Колонія комарів має початкову популяцію 1000. Через\(t\) добу популяція дається по\(A(t)=1000e^{0.3t}\). Показати, що відношення темпів зміни населення\(A′(t)\), до населення,\(A(t)\) постійне.
Рішення
Перша знахідка\(A′(t)\). Використовуючи правило ланцюга, ми маємо.\(A′(t)=300e^{0.3t}.\) Таким чином, відношення швидкості зміни популяції до населення задається
\[\frac{A′(t)}{A(t)}=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \nonumber \]
Ставлення темпів зміни популяції до населення - постійне 0,3.
Якщо\(A(t)=1000e^{0.3t}\) описується популяція комарів через\(t\) дні, як в попередньому прикладі, то яка швидкість зміни\(A(t)\) через 4 дні?
- Підказка
-
Знайти\(A′(4)\).
- Відповідь
-
\(996\)
Похідна логарифмічної функції
Тепер, коли ми маємо похідну природної експоненціальної функції, ми можемо використовувати неявну диференціацію, щоб знайти похідну від її зворотної, природної логарифмічної функції.
Якщо\(x>0\) і\(y=\ln x\), то
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
Більш загально, нехай\(g(x)\) буде диференційована функція. Для всіх значень,\(x\) для яких\(g′(x)>0\), похідна від\(h(x)=\ln(g(x))\) задається
\[h′(x)=\frac{1}{g(x)}g′(x). \nonumber \]
Якщо\(x>0\) і\(y=\ln x\), то\(e^y=x.\) диференціація обох сторін цього рівняння призводить до рівняння
\[e^y\frac{dy}{dx}=1. \nonumber \]
Рішення для\(\dfrac{dy}{dx}\) врожайності
\[\frac{dy}{dx}=\frac{1}{e^y}. \nonumber \]
Нарешті, підставляємо\(x=e^y\) для отримання
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
Ми також можемо отримати цей результат, застосувавши теорему оберненої функції наступним чином. Так як\(y=g(x)=\ln x\)
є оберненою\(f(x)=e^x\), застосовуючи обернену функцію теореми ми маємо
\[\frac{dy}{dx}=\frac{1}{f′(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \nonumber \]
Використання цього результату та застосування правила ланцюга до\(h(x)=\ln(g(x))\) прибутковості
\[h′(x)=\frac{1}{g(x)}g′(x). \label{lnder} \]
□
Графік\(y=\ln x\) і його похідна\(\dfrac{dy}{dx}=\dfrac{1}{x}\) наведені на рис\(\PageIndex{3}\).
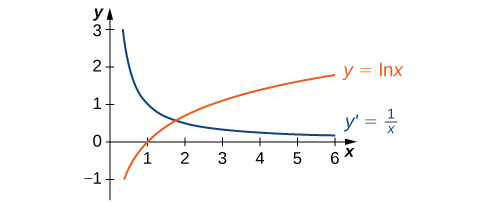
Знайдіть похідну від\(f(x)=\ln(x^3+3x−4)\).
Рішення
Використовуйте рівняння\ ref {lnder} безпосередньо.
\ (\ begin {align*} f′ (x) &=\ dfrac {1} {x^3+3x−4} ⋅ (3x^2+3) &\ текст {Використовувати} g (x) =x^3+3x−4\ текст {in} h′ (x) =\ dfrac {1} {g (x)} g′ (x).\\ 4 pt]
&=\ dfrac {3x^2+3} {x^3+3x−4} &\ текст {Переписати.} \ end {вирівнювати*}\)
Знайдіть похідну від\(f(x)=\ln\left(\dfrac{x^2\sin x}{2x+1}\right)\).
Рішення
На перший погляд, взяття цієї похідної представляється досить складним. Однак, використовуючи властивості логарифмів до знаходження похідної, ми можемо значно спростити задачу.
\ (\ begin {align*} f (x) &=\ ln\ ліворуч (\ frac {x^2\ sin x} {2x+1}\ праворуч) =2\ ln x′\ ln (\ sin x) −\ ln (2x+1) &\ text {Застосувати властивості логарифмів.}\\ [4pt]
f′ (x) &=\ dfrac {2} {x} +\ cot x−\ dfrac {2} {2x+1} &\ text {Застосувати правило суми та} h′ (x) =\ dfrac {1} {g (x)} g′ (x). \ end {вирівнювати*}\)
Диференціювати:\(f(x)=\ln(3x+2)^5\).
- Підказка
-
Використовуйте властивість логарифмів для спрощення перед прийняттям похідної.
- Відповідь
-
\(f′(x)=\dfrac{15}{3x+2}\)
Тепер, коли ми можемо диференціювати природні логарифмічні функції, ми можемо використовувати цей результат, щоб знайти похідні\(y=\log_b x\) і\(y=b^x\) для\(b>0, \,b≠1\).
Нехай\(b>0,b≠1,\) і\(g(x)\) нехай диференційована функція.
i. якщо\(y=\log_b x\), то
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
Більш загально, якщо\(h(x)=\log_b(g(x))\), то для всіх значень,\(x\) для яких\(g(x)>0\),
\[h′(x)=\frac{g′(x)}{g(x)\ln b}. \label{genlogder} \]
II. Якщо\(y=b^x,\) тоді
\[\frac{dy}{dx}=b^x\ln b. \nonumber \]
Більш загально, якщо\(h(x)=b^{g(x)},\) тоді
\[h′(x)=b^{g(x)}g'(x)\ln b \label{genexpder} \]
Якщо\(y=\log_b x,\) тоді\(b^y=x.\) випливає, що\(\ln(b^y)=\ln x\). Таким чином\(y\ln b=\ln x\). Рішення для\(y\), ми маємо\(y=\dfrac{\ln x}{\ln b}\). Диференціюючи і маючи на увазі, що\(\ln b\) це константа, ми бачимо, що
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
Похідна в Equation\ ref {genlogder} тепер випливає з правила ланцюга.
Якщо\(y=b^x\). то\(\ln y=x\ln b.\) Використовуючи неявну диференціацію, знову маючи на увазі, що\(\ln b\) є постійним, випливає, що\(\dfrac{1}{y}\dfrac{dy}{dx}=\ln b\). Вирішуючи\(\dfrac{dy}{dx}\) і підставляючи\(y=b^x\), ми бачимо, що
\[\frac{dy}{dx}=y\ln b=b^x\ln b. \nonumber \]
Більш загальна похідна (Equation\ ref {genexpder}) випливає з правила ланцюга.
□
Знайдіть похідну від\(h(x)=\dfrac{3^x}{3^x+2}\).
Рішення
Використовуйте часткове правило і Примітка.
\ (\ begin {align*} h′ (x) &=\ dfrac {3^x\ ln 3 (3^x+2) −3^x\ ln 3 (3^x)} {(3^x+2) ^2} &\ text {Застосувати правило частки.}\\ [4pt]
&=\ dfrac {2⋅3^x\ ln 3} {(3xx\ ln 3} +2) ^2} &\ текст {Спрощення.} \ end {вирівнювати*}\)
Знайти нахил прямої дотичної до графіка\(y=\log_2 (3x+1)\) at\(x=1\).
Рішення
Щоб знайти ухил, ми повинні оцінити\(\dfrac{dy}{dx}\) на\(x=1\). Використовуючи рівняння\ ref {genlogder}, ми бачимо, що
\[\frac{dy}{dx}=\frac{3}{(3x+1)\ln 2}. \nonumber \]
Оцінюючи похідну в\(x=1\), ми бачимо, що дотична лінія має нахил
\[\frac{dy}{dx}\bigg{|}_{x=1}=\frac{3}{4\ln 2}=\frac{3}{\ln 16}. \nonumber \]
Знайти нахил для прямої дотичної до\(y=3^x\) at\(x=2.\)
- Підказка
-
Оцініть похідну при\(x=2.\)
- Відповідь
-
\(9\ln(3)\)
Логарифмічна диференціація
У цей момент ми можемо приймати похідні функцій виду\(y=(g(x))^n\) для певних значень\(n\), а також функції виду\(y=b^{g(x)}\), де\(b>0\) і\(b≠1\). На жаль, ми досі не знаємо похідних функцій, таких як\(y=x^x\) або\(y=x^π\). Ці функції вимагають техніки, яка називається логарифмічною диференціацією, яка дозволяє диференціювати будь-яку функцію форми\(h(x)=g(x)^{f(x)}\). Він також може бути використаний для перетворення дуже складної задачі диференціації в простішу, наприклад, пошук похідної від\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\). Ми окреслимо цю техніку в наступній стратегії вирішення проблем.
- Для диференціації\(y=h(x)\) за допомогою логарифмічної диференціації візьміть натуральний логарифм обох сторін рівняння для отримання\(\ln y=\ln(h(x)).\)
- Використовуйте властивості логарифмів, щоб\(\ln(h(x))\) максимально розширити.
- Диференціювати обидві сторони рівняння. Зліва у нас буде\(\dfrac{1}{y}\dfrac{dy}{dx}\).
- Помножте обидві сторони рівняння на\(y\), щоб вирішити для\(\dfrac{dy}{dx}\).
- Замінити\(y\) на\(h(x)\).
Знайдіть похідну від\(y=(2x^4+1)^{\tan x}\).
Рішення
Використовуйте логарифмічну диференціацію, щоб знайти цю похідну.
\ (\ begin {align*}\ ln y&=\ ln (2x^4+1) ^ {\ tan x} &\ text {Крок 1. Візьміть натуральний логарифм обох сторін.}\\ [4pt]
\ ln y&=\ tan x\ ln (2x^4+1) &\ text {Крок 2. Розгорніть за допомогою властивостей логарифмів.}\\ [4pt]
\ dfrac {1} {y}\ dfrac {dy} {dx} &=\ sec^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x & &\ text {Крок 3. Диференціювати обидві сторони. Використовуйте правило продукту праворуч.}\\ [4pt]
\ dfrac {dy} {dx} &=y⋅ (\ sec ^ 2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x) &\ текст {Крок 4. Помножте на} y\ текст {з обох сторін.}\\ [4pt]
\ dfrac {dy} {dx} & =( 2x^4+1) ^ {\ tan x} (\ сек ^ 2 х\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x) &\ текст {Крок 5. Заміна} y= (2x^4+1) ^ {\ tan x}. \ end {вирівнювати*}\)
Знайдіть похідну від\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\).
Рішення
Ця проблема дійсно використовує властивості логарифмів та правила диференціації, наведені в цьому розділі.
| \(\ln y=\ln\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\) | Крок 1. Візьміть натуральний логарифм обох сторін. |
| \(\ln y=\ln x+\frac{1}{2}\ln(2x+1)−x\ln e−3\ln \sin x\) | Крок 2. Розгорніть за допомогою властивостей логарифмів. |
| \(\dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\dfrac{\cos x}{\sin x}\) | Крок 3. Диференціювати обидві сторони. |
| \(\dfrac{dy}{dx}=y\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Крок 4. Помножте\(y\) на обидві сторони. |
| \(\dfrac{dy}{dx}=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Крок 5. Замінник\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}.\) |
Використовуйте логарифмічну диференціацію, щоб знайти похідну від\(y=x^x\).
- Підказка
-
Дотримуйтесь стратегії вирішення проблем.
- Відповідь
-
Рішення:\(\dfrac{dy}{dx}=x^x(1+\ln x)\)
Знайдіть похідну від\(y=(\tan x)^π\).
- Підказка
-
Використовуйте правило потужності (так як показник\(\pi\) є постійною) і правило ланцюга.
- Відповідь
-
\(y′=π(\tan x)^{π−1}\sec^2 x\)
Ключові концепції
- На підставі припущення, що експоненціальна функція\(y=b^x, \,b>0\) всюди безперервна і диференційовна при\(0\), ця функція диференційовна всюди і існує формула її похідної.
- Ми можемо використовувати формулу, щоб знайти похідну\(y=\ln x\), і зв'язок\(\log_b x=\dfrac{\ln x}{\ln b}\) дозволяє нам розширити наші формули диференціації, включивши логарифми з довільними основами.
- Логарифмічна диференціація дозволяє диференціювати функції виду\(y=g(x)^{f(x)}\) або дуже складні функції, приймаючи природний логарифм обох сторін і використовуючи властивості логарифмів перед диференціацією.
Ключові рівняння
- Похідна природної експоненціальної функції
\(\dfrac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x)\)
- Похідна натуральної логарифмічної функції
\(\dfrac{d}{dx}\Big(\ln g(x)\Big)=\dfrac{1}{g(x)}g′(x)\)
- Похідна загальної експоненціальної функції
\(\dfrac{d}{dx}\Big(b^{g(x)}\Big)=b^{g(x)}g′(x)\ln b\)
- Похідна загальної логарифмічної функції
\(\dfrac{d}{dx}\Big(\log_b g(x)\Big)=\dfrac{g′(x)}{g(x)\ln b}\)
Глосарій
- логарифмічна диференціація
- - це техніка, яка дозволяє диференціювати функцію, спочатку взявши натуральний логарифм обох сторін рівняння, застосовуючи властивості логарифмів для спрощення рівняння та диференціюючи неявно
